人教版数学八年级上册课件:14.3.2(1)公式法——用平方差公式分解因式(25张)
文档属性
| 名称 | 人教版数学八年级上册课件:14.3.2(1)公式法——用平方差公式分解因式(25张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 681.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 00:00:00 | ||
图片预览








文档简介
14.3.2(1) 公式法
——用平方差公式分解因式
洛阳双语学校数学教研组
预习与反馈
1、知识回顾:
2、确定公因式的方法:一看系数; 二看字母; 三看指数
3、提公因式法分解因式步骤(分三步):
第一步,确定公因式;第二步,求出另一个因式
第三步, 写成积的形式
1、因式分解:
4、用提公因式法分解因式应注意的问题:
(1)公因式要提尽;
(2)小心漏项;
(3)多项式的首项取正号;
整式、积的形式
2、预习指导:
(1)预习提示:预习教材116——117页的内容;
(2)预习反馈:完成《四清导航》第66页 预习导航
(3)预习思考:
学习目标:
1.探索并运用平方差公式进行因式分解,体会转化思想。
2.会综合运用提公因式法和平方差公式对多项式进行因式分解.
学习重点:
运用平方差公式来分解因式.
思考探究:
(1)本题你能用提公因式法分解因式吗?
(2)这两个多项式有什么共同的特点?
(3)你能利用整式的乘法公式——平方差公式
来解决这个问题吗?
你能将多项式 与多项式 分解因式吗?
新课精讲
你对因式分解的方法有什么新的发现?请尝试着概括你的发现.
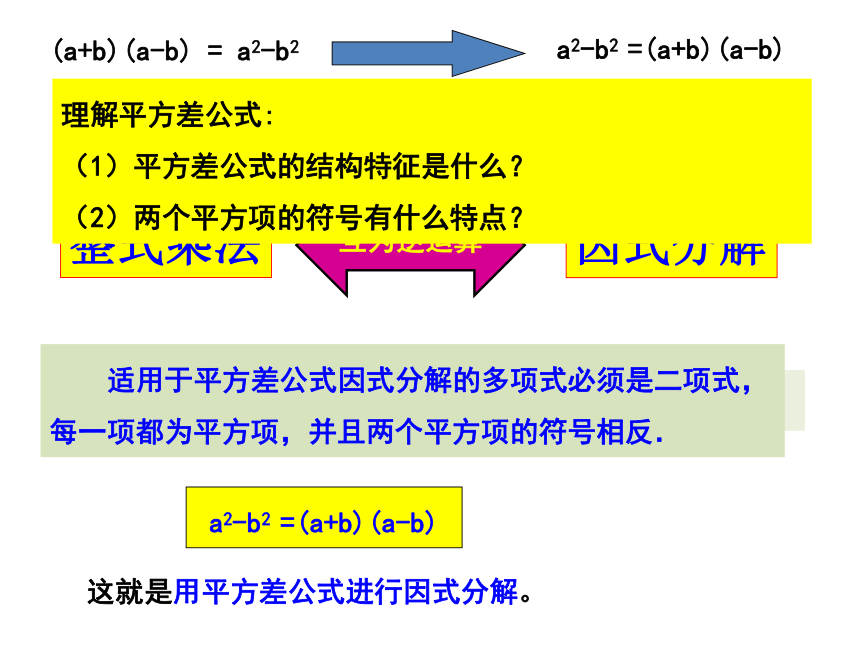
(a+b)(a-b) = a2-b2
a2-b2 =(a+b)(a-b)
两个数的平方差,等于这两个数的和与这两个数的差的积。
整式乘法
因式分解
a2-b2 =(a+b)(a-b)
这就是用平方差公式进行因式分解。
互为逆运算
能用则用
理解平方差公式:
(1)平方差公式的结构特征是什么?
(2)两个平方项的符号有什么特点?
适用于平方差公式因式分解的多项式必须是二项式,每一项都为平方项,并且两个平方项的符号相反.
例3、分解因式:
(1) 4x2–9 ; (2) (x+p)2–(x+q)2.
分析:
在(1)中,4x2 = (2x)2,9=32,4x2-9 = (2x )2 –3 2,
即可用平方差公式分解因式.
在(2)中,把(x+p)和 (x+q)各看成一个整体,设x+p=m,x+q=n,则原式化为m2-n2.
4x2–9
= (2x)2–32
= (2x+3)(2x–3).
(x+p)2 –(x+q) 2
=[(x+p)+(x+q)][(x+p)–(x+q)]
=(2x+p+q)(p–q).
例4 、分解因式: (1)x4—y4; (2) a3b —ab.
分析:
(1)x4-y4写成(x2)2 - (y2)2的形式,这样就可以利用平方差公式进行因式分解了.
(2)a3b-ab有公因式ab,应先提出公因式,再进一步分解.
解:(1) x4-y4
= (x2)2-(y2 )2
= (x2+y2)(x2-y2)
= (x2+y2)(x+y)(x-y).
(2) a3b-ab
=ab(a2- 1)
=ab(a+1)(a-1).
分解彻底
补充例题、将下列各式分解因式:
(1)(x-y)2-1
(1)(x-y)2-1
=[ (x-y)+1 ] [(x-y)-1 ]
=(x-y+1)(x-y-1).
(2)xn+3-xn-1 =xn-1x4-xn-1
=xn-1(x4-1)
=xn-1(x2+1)(x2-1)
=xn-1(x2+1)(x +1)(x -1)
分解彻底
(2)xn+3-xn-1
在实数范围内分解因式:(3)x4-4; (4)2x4-50
解: (3)(x2+2)(x2-2)
解:(4)2(x4-25)
=(x2+2)(x+ )(x- )
= 2(x2+5)(x2-5)
=2(x2 +5)(x+ )(x- )
【规律总结】
分解因式问题,先考虑提取公因式,再考虑使用公式(如:平方差公式)。
凡是符合平方差公式左边特点的二项式,都可以运用平方差公式分解因式.
1.下列多项式能否用平方差公式来分解因式?为什么?
(1) x2+y2 ; (2) x2-y2;
(3) -x2+y2; (4) -x2-y2.
2.分解因式:
(1)a2- b2; (2)9a2-4b2;
(3) x2y-4y ; (4) -a4 +16.
(a+ b)(a - b )
(3a+2b)(3a-2b)
y(x+2)(x-2)
(4+a2)(2+a)(2-a)
课本117页练习题
【合作探究】
1、把下列各式分解因式:(2x-1)2-(x+2)2;
解:原式=[ (2x-1)+(x+2) ][ (2x-1)-(x+2) ]
=(3x+1)(x-3).
2、分解因式(1)4m3n-16mn3;(2)(a-b)3-a+b
(1)、4mn(m+2n)(m-2n)
(2)、(a-b)(a-b+1)(a-b-1)
反馈练习
点拨精讲:先分解因式后计算出来,再约分。
小结测试
课本119页:2、4
作业布置
计算:
1002-992+982-972+962-952+… +22-12
解:原式
=(100+99)(100-99)+(98+97)(98-97)+… +(2+1)(2-1)
=100+99+98+97 +… +2+1
=5050
一、预习与反馈
知识回顾 :
预习效果反馈
1、 课后170页习题
2、《优化设计》快乐预习
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
完全平方公式
思考:如何将多项式a2+2ab+b2 与a2-2ab+b2分解因式?
(a+b)2=a2+2ab+b2,
(a-b)2=a2-2ab+b2.
a2+2ab+b2=(a+b)2
a2-2ab+b2=(a-b)2
完全平方式的特点:
1、必须是三项式;
2、首尾平方乘积二倍;
一般地,利用公式a2-b2=(a+b)(a-b),或(a2±2ab+b2)=(a±b)2把一个多项式分解因式的方法,叫做公式法.公式中的a, b可以是数,也可以是整式.
二、新课精讲
互为逆运算
例5 、分解因式:
(1) 16x2+24x+9; (2) –x2+4xy–4y2.
分析:在(1)中,16x2=(4x)2,9=32,24x=2·4x·3,所以16x2+24x+9是一个完全平方式,即
16x2+24x+9=(4x)2+2·4x·3+32
解:(1)16x2+24x+9
= (4x)2+2·4x·3+32
=(4x+3)2.
(2) -x2+4xy-4y2
= - (x2-4xy+4y2)
= - [x2-2·x·2y+(2y)2]
= - (x-2y)2 .
例6 分解因式:
(1) 3ax2+6axy+3ay2; (2) (a+b)2-12(a+b)+36.
分析:在(1)中有公因式3a,应先提出公因式,再进一步分解.
解:(1)3ax2+6axy+3ay2
=3a(x2+2xy+y2)
=3a(x+y)2 .
(2)(a+b)2-12(a+b)+36
=(a+b)2-2·(a+b)·6+62
=(a+b-6)2.
练 习
1.下列多项式是不是完全平方式?为什么?
(1) a2-4a+4; (2)1+4a2;
(3) 4b2+4b-1 ; (4)a2+ab+b2.
2.分解因式:
(1) x2+12x+36; (2) -2xy-x2-y2;
(3) a2+2a+1; (4) 4x2-4x+1;
(5) ax2+2a2x+a3; (6) -3x2+6xy-3y2.
拓展:
例1:分解因式: (1)y2-4x(y-x); (2)(a2+b2)2-4a2b2.
解:(1)y2-4x(y-x)
=y2-4xy+4x2
=(y-2x)2.
(2)(a2+b2)2-4a2b2
=(a2+b2)2-(2ab)2
=(a2+b2+2ab)(a2+b2-2ab)
=(a+b)2(a-b)2.
例2、分解因式: 36m2a-9m2a2-36m2
解:36m2a-9m2a2-36m2
=-9m2(a2-4a+4)
=-9m2(a-2)2.
【规律总结】
分解因式问题,先考虑提取公因式,再考虑使用公式(如:完全平方公式)。
凡是符合完全平方公式左边特点的三项式,都可以运用完全平方公式分解因式.
总结归纳:
(1) 先提公因式(有的话);
(2) 利用公式(可以的话);
(3) 分解因式时要分解到不能分解为止.
①若为二项式,考虑用平方差公式;
②若为三项式,考虑用完全平方公式.
三、反馈练习
A
1.下列代数式中,是完全平方式的有(
)
③4y2-4y+1;
①a2-4a+4;
②9a2+16b2-20ab;
A.①③
B.②④
C.③④
D.①⑤
2.把代数式 ax2-4ax+4a 分解因式,下列结果中正确的是( )
A
A.a(x-2)2
C.a(x-4)2
B.a(x+2)2
D.a(x+2)(x-2)
3 . 把 多 项 式 2mx2 - 4mxy + 2my2分 解 因 式 的 结 果是:
2m(x-y)2
4.把下列各式分解因式(1)2ab-a2 -b2+4;
(2)(2a+b)2-8ab
解:(1)(2+a-b)(2-a+b); (2)(2a-b)2。
④6x2+3x+1;
⑤x2+4xy+2y2.
◆仔细做一做:
分解因式:(x+y)2+4(x-y)2-4(x2-y2).
◆创新应用:
已知(a+2b)2-2a-4b+1=0,求(a+2b)2011的值.
◆综合拓展:
已知△ABC的三边分别为a,b,c,且a,b,c满足等式3(a2+b2+c2)=(a+b+c)2,请你说明△ABC是等边三角形.
四、小结测试
《练闯考》第89页第1—7题
五、作业
作业: P171页
第3(2)(4)(6)和第5题。
——用平方差公式分解因式
洛阳双语学校数学教研组
预习与反馈
1、知识回顾:
2、确定公因式的方法:一看系数; 二看字母; 三看指数
3、提公因式法分解因式步骤(分三步):
第一步,确定公因式;第二步,求出另一个因式
第三步, 写成积的形式
1、因式分解:
4、用提公因式法分解因式应注意的问题:
(1)公因式要提尽;
(2)小心漏项;
(3)多项式的首项取正号;
整式、积的形式
2、预习指导:
(1)预习提示:预习教材116——117页的内容;
(2)预习反馈:完成《四清导航》第66页 预习导航
(3)预习思考:
学习目标:
1.探索并运用平方差公式进行因式分解,体会转化思想。
2.会综合运用提公因式法和平方差公式对多项式进行因式分解.
学习重点:
运用平方差公式来分解因式.
思考探究:
(1)本题你能用提公因式法分解因式吗?
(2)这两个多项式有什么共同的特点?
(3)你能利用整式的乘法公式——平方差公式
来解决这个问题吗?
你能将多项式 与多项式 分解因式吗?
新课精讲
你对因式分解的方法有什么新的发现?请尝试着概括你的发现.
(a+b)(a-b) = a2-b2
a2-b2 =(a+b)(a-b)
两个数的平方差,等于这两个数的和与这两个数的差的积。
整式乘法
因式分解
a2-b2 =(a+b)(a-b)
这就是用平方差公式进行因式分解。
互为逆运算
能用则用
理解平方差公式:
(1)平方差公式的结构特征是什么?
(2)两个平方项的符号有什么特点?
适用于平方差公式因式分解的多项式必须是二项式,每一项都为平方项,并且两个平方项的符号相反.
例3、分解因式:
(1) 4x2–9 ; (2) (x+p)2–(x+q)2.
分析:
在(1)中,4x2 = (2x)2,9=32,4x2-9 = (2x )2 –3 2,
即可用平方差公式分解因式.
在(2)中,把(x+p)和 (x+q)各看成一个整体,设x+p=m,x+q=n,则原式化为m2-n2.
4x2–9
= (2x)2–32
= (2x+3)(2x–3).
(x+p)2 –(x+q) 2
=[(x+p)+(x+q)][(x+p)–(x+q)]
=(2x+p+q)(p–q).
例4 、分解因式: (1)x4—y4; (2) a3b —ab.
分析:
(1)x4-y4写成(x2)2 - (y2)2的形式,这样就可以利用平方差公式进行因式分解了.
(2)a3b-ab有公因式ab,应先提出公因式,再进一步分解.
解:(1) x4-y4
= (x2)2-(y2 )2
= (x2+y2)(x2-y2)
= (x2+y2)(x+y)(x-y).
(2) a3b-ab
=ab(a2- 1)
=ab(a+1)(a-1).
分解彻底
补充例题、将下列各式分解因式:
(1)(x-y)2-1
(1)(x-y)2-1
=[ (x-y)+1 ] [(x-y)-1 ]
=(x-y+1)(x-y-1).
(2)xn+3-xn-1 =xn-1x4-xn-1
=xn-1(x4-1)
=xn-1(x2+1)(x2-1)
=xn-1(x2+1)(x +1)(x -1)
分解彻底
(2)xn+3-xn-1
在实数范围内分解因式:(3)x4-4; (4)2x4-50
解: (3)(x2+2)(x2-2)
解:(4)2(x4-25)
=(x2+2)(x+ )(x- )
= 2(x2+5)(x2-5)
=2(x2 +5)(x+ )(x- )
【规律总结】
分解因式问题,先考虑提取公因式,再考虑使用公式(如:平方差公式)。
凡是符合平方差公式左边特点的二项式,都可以运用平方差公式分解因式.
1.下列多项式能否用平方差公式来分解因式?为什么?
(1) x2+y2 ; (2) x2-y2;
(3) -x2+y2; (4) -x2-y2.
2.分解因式:
(1)a2- b2; (2)9a2-4b2;
(3) x2y-4y ; (4) -a4 +16.
(a+ b)(a - b )
(3a+2b)(3a-2b)
y(x+2)(x-2)
(4+a2)(2+a)(2-a)
课本117页练习题
【合作探究】
1、把下列各式分解因式:(2x-1)2-(x+2)2;
解:原式=[ (2x-1)+(x+2) ][ (2x-1)-(x+2) ]
=(3x+1)(x-3).
2、分解因式(1)4m3n-16mn3;(2)(a-b)3-a+b
(1)、4mn(m+2n)(m-2n)
(2)、(a-b)(a-b+1)(a-b-1)
反馈练习
点拨精讲:先分解因式后计算出来,再约分。
小结测试
课本119页:2、4
作业布置
计算:
1002-992+982-972+962-952+… +22-12
解:原式
=(100+99)(100-99)+(98+97)(98-97)+… +(2+1)(2-1)
=100+99+98+97 +… +2+1
=5050
一、预习与反馈
知识回顾 :
预习效果反馈
1、 课后170页习题
2、《优化设计》快乐预习
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
完全平方公式
思考:如何将多项式a2+2ab+b2 与a2-2ab+b2分解因式?
(a+b)2=a2+2ab+b2,
(a-b)2=a2-2ab+b2.
a2+2ab+b2=(a+b)2
a2-2ab+b2=(a-b)2
完全平方式的特点:
1、必须是三项式;
2、首尾平方乘积二倍;
一般地,利用公式a2-b2=(a+b)(a-b),或(a2±2ab+b2)=(a±b)2把一个多项式分解因式的方法,叫做公式法.公式中的a, b可以是数,也可以是整式.
二、新课精讲
互为逆运算
例5 、分解因式:
(1) 16x2+24x+9; (2) –x2+4xy–4y2.
分析:在(1)中,16x2=(4x)2,9=32,24x=2·4x·3,所以16x2+24x+9是一个完全平方式,即
16x2+24x+9=(4x)2+2·4x·3+32
解:(1)16x2+24x+9
= (4x)2+2·4x·3+32
=(4x+3)2.
(2) -x2+4xy-4y2
= - (x2-4xy+4y2)
= - [x2-2·x·2y+(2y)2]
= - (x-2y)2 .
例6 分解因式:
(1) 3ax2+6axy+3ay2; (2) (a+b)2-12(a+b)+36.
分析:在(1)中有公因式3a,应先提出公因式,再进一步分解.
解:(1)3ax2+6axy+3ay2
=3a(x2+2xy+y2)
=3a(x+y)2 .
(2)(a+b)2-12(a+b)+36
=(a+b)2-2·(a+b)·6+62
=(a+b-6)2.
练 习
1.下列多项式是不是完全平方式?为什么?
(1) a2-4a+4; (2)1+4a2;
(3) 4b2+4b-1 ; (4)a2+ab+b2.
2.分解因式:
(1) x2+12x+36; (2) -2xy-x2-y2;
(3) a2+2a+1; (4) 4x2-4x+1;
(5) ax2+2a2x+a3; (6) -3x2+6xy-3y2.
拓展:
例1:分解因式: (1)y2-4x(y-x); (2)(a2+b2)2-4a2b2.
解:(1)y2-4x(y-x)
=y2-4xy+4x2
=(y-2x)2.
(2)(a2+b2)2-4a2b2
=(a2+b2)2-(2ab)2
=(a2+b2+2ab)(a2+b2-2ab)
=(a+b)2(a-b)2.
例2、分解因式: 36m2a-9m2a2-36m2
解:36m2a-9m2a2-36m2
=-9m2(a2-4a+4)
=-9m2(a-2)2.
【规律总结】
分解因式问题,先考虑提取公因式,再考虑使用公式(如:完全平方公式)。
凡是符合完全平方公式左边特点的三项式,都可以运用完全平方公式分解因式.
总结归纳:
(1) 先提公因式(有的话);
(2) 利用公式(可以的话);
(3) 分解因式时要分解到不能分解为止.
①若为二项式,考虑用平方差公式;
②若为三项式,考虑用完全平方公式.
三、反馈练习
A
1.下列代数式中,是完全平方式的有(
)
③4y2-4y+1;
①a2-4a+4;
②9a2+16b2-20ab;
A.①③
B.②④
C.③④
D.①⑤
2.把代数式 ax2-4ax+4a 分解因式,下列结果中正确的是( )
A
A.a(x-2)2
C.a(x-4)2
B.a(x+2)2
D.a(x+2)(x-2)
3 . 把 多 项 式 2mx2 - 4mxy + 2my2分 解 因 式 的 结 果是:
2m(x-y)2
4.把下列各式分解因式(1)2ab-a2 -b2+4;
(2)(2a+b)2-8ab
解:(1)(2+a-b)(2-a+b); (2)(2a-b)2。
④6x2+3x+1;
⑤x2+4xy+2y2.
◆仔细做一做:
分解因式:(x+y)2+4(x-y)2-4(x2-y2).
◆创新应用:
已知(a+2b)2-2a-4b+1=0,求(a+2b)2011的值.
◆综合拓展:
已知△ABC的三边分别为a,b,c,且a,b,c满足等式3(a2+b2+c2)=(a+b+c)2,请你说明△ABC是等边三角形.
四、小结测试
《练闯考》第89页第1—7题
五、作业
作业: P171页
第3(2)(4)(6)和第5题。
