人教版数学七年级下册7.1.2平面直角坐标系课件(17张)
文档属性
| 名称 | 人教版数学七年级下册7.1.2平面直角坐标系课件(17张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 604.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 20:04:21 | ||
图片预览




文档简介
平面直角坐标系
1、什么叫数轴?
规定了原点、正方向、单位长度的直线叫做数轴。
复习
数轴上的点和实数一一对应。
2、什么叫有序数对?
有顺序的两个数a与b组成的数对叫做有序数对,记作(a,b)
如何确定直线上点的位置?
?
0
-1
-2
-3
1
2
3
4
A
B
?
x轴或横轴
y轴或纵轴
原点
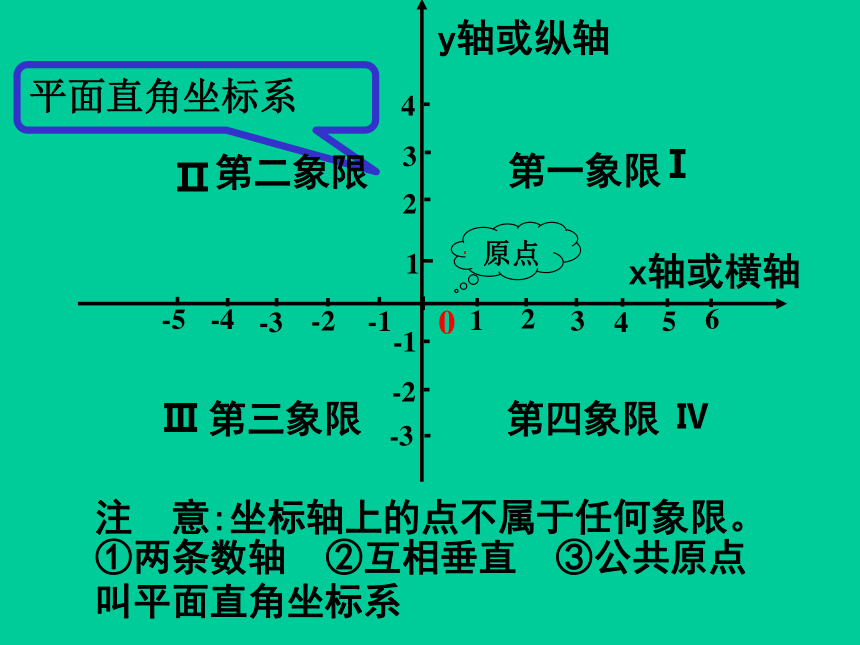
①两条数轴 ②互相垂直 ③公共原点 叫平面直角坐标系
平面直角坐标系
第一象限
第二象限
第三象限
第四象限
注
意:坐标轴上的点不属于任何象限。
-1
-2
-3
1
2
3
4
0
-5
-4
-3
-2
-1
3
4
2
1
5
6
Ⅰ
Ⅲ
Ⅱ
Ⅳ
·
A
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
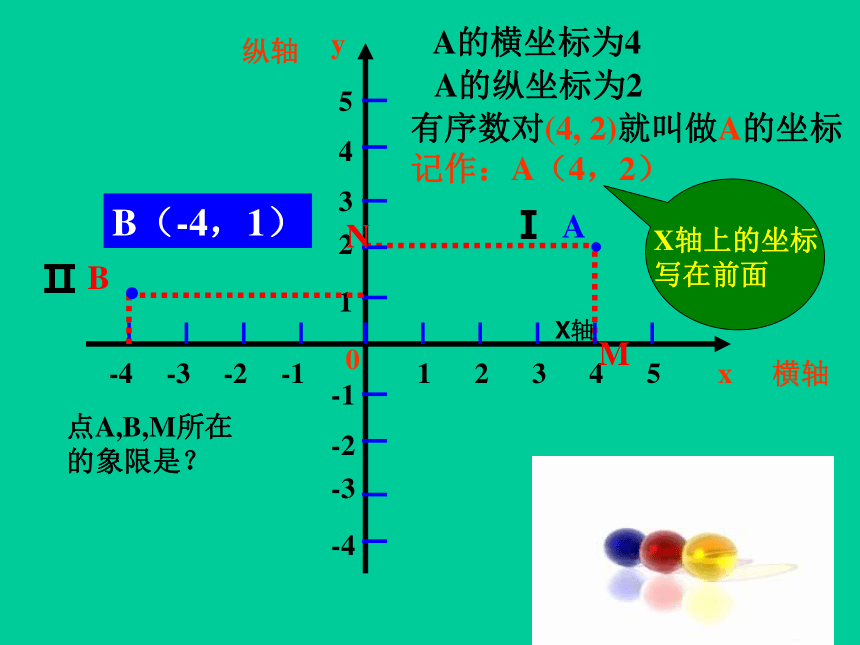
A的横坐标为4
A的纵坐标为2
有序数对(4,
2)就叫做A的坐标
记作:A(4,2)
X轴上的坐标
写在前面
·
B
B(-4,1)
M
N
点A,B,M所在的象限是?
Ⅰ
Ⅱ
X轴
·
B
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
·
C
·
A
·
G
·
E
(
2,3
)
(
3,2
)
(
-2,1
)
(
-4,-
3
)
(
1,-
2
)
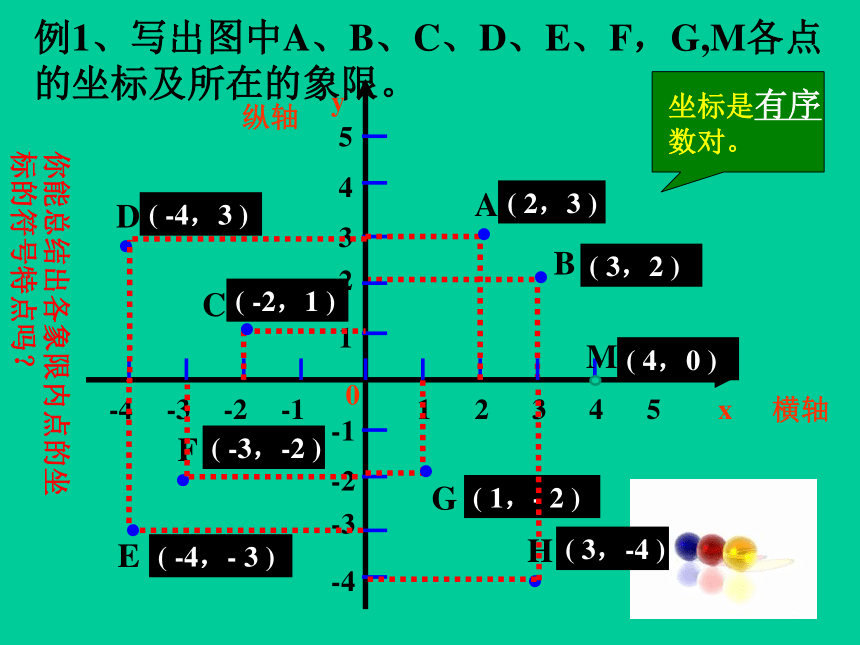
坐标是有序
数对。
例1、写出图中A、B、C、D、E、F,G,M各点的坐标及所在的象限。
M
(
4,0
)
·
D
(
-4,3
)
·
F
(
-3,-2
)
·
H
(
3,-4
)
你能总结出各象限内点的坐标的符号特点吗?
第一象限:(正,正)
第二象限:(负,正)
第三象限:(负,负)
第四象限:(正,负)
你能说出各个象限内
的特点吗?
1
2
3
-3
x
-2
·
-2
-3
o
-1
y
4
2
5
3
6
1
在如图建立的直角坐标系中描出下列各组点,并将各组点用线段依次连接起来.
做
一
做
①(0
,
6),
(-4,
3),
(4
,
3)
②(-2
,
3),
(-2
,
-3),
(2
,
-3),
(2
,
3)
·
·
·
·
·
·
观察所得的图形,你觉得它象什么?
-4
-1
4
A(-4,3)
B(4,3)
C(-2,3)
D(2,3)
E(-2,-3)
F(2,-3)
(0
,
6)
·
例
2、
A
B
C
D
E
F
例3、写出图中多边形ABCDEF各个顶点的坐标。
(-2,0)
(0,-3)
(3,-3)
(4,0)
(3,3)
(0,3)
例3、观察:(1)点E,F的坐标有什么特点?线段EF与x轴、y轴有什么关系?
(2)点E,C的坐标有什么特点,线段EC与x轴、y轴有什么关系?
(3)x轴上的点的特点;y轴上的点的特点?
结论
纵坐标相同的点的连线平行于x轴
横坐标相同的点的连线平行于y轴
坐标轴上的点至少有一个是0
x轴上的点纵坐标为0,
y轴上的点横坐标为0.
(垂直于y轴)
(垂直于x轴)
你知道吗?
早在1637年以前,法国数学家、解析几何的创始人笛卡尔受到了经纬度的启发,地理上的经纬度是以赤道和本初子午线为标准的,这两条线从局部上可以看成是平面内互相垂直的两条直线。所以笛卡尔的方法是在平面内画两条互相垂直的数轴,其中水平的数轴叫x轴(或横轴),取向右为正方向,铅直的数轴叫y轴(或纵轴),取向上为正方向,它们的交点是原点,这个平面叫坐标平面。
告诉大家
本节课你学会了什么!
小结:
这节课主要学面直角坐标系的有
关概念。掌握:
1.
会根据坐标找点,会由坐标系内的点写坐标
2.x轴,y轴上点的坐标的特点:
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
第一象限:(+,
+)
第二象限:(—,
+)
第三象限:(—,—)
第四象限:(+,
—)
再见
A(6,-2),
B(0,3)
,
C(3,7),
D(-6,-3),
E(-2,0)
,
F(-9,5)
练一练
分别说出下列各点在哪个象限内或在哪条坐标轴上?
第一象限:(正,正)
第二象限:(负,正)
第三象限:(负,负)
第四象限:(正,负)
x轴:纵坐标为0;y轴:横坐标为0
雁塔
中心广场
钟楼
大成殿
科枝大学
碑林
影月湖
如果以“中心广场”为原点作两条相互垂直的数轴,分别取向右和向上的方向为数轴的正方向,一个方格的边长看做一个单位长度,那么你能表示“碑林”的位置吗?“大成殿”的位置呢?
1、什么叫数轴?
规定了原点、正方向、单位长度的直线叫做数轴。
复习
数轴上的点和实数一一对应。
2、什么叫有序数对?
有顺序的两个数a与b组成的数对叫做有序数对,记作(a,b)
如何确定直线上点的位置?
?
0
-1
-2
-3
1
2
3
4
A
B
?
x轴或横轴
y轴或纵轴
原点
①两条数轴 ②互相垂直 ③公共原点 叫平面直角坐标系
平面直角坐标系
第一象限
第二象限
第三象限
第四象限
注
意:坐标轴上的点不属于任何象限。
-1
-2
-3
1
2
3
4
0
-5
-4
-3
-2
-1
3
4
2
1
5
6
Ⅰ
Ⅲ
Ⅱ
Ⅳ
·
A
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
A的横坐标为4
A的纵坐标为2
有序数对(4,
2)就叫做A的坐标
记作:A(4,2)
X轴上的坐标
写在前面
·
B
B(-4,1)
M
N
点A,B,M所在的象限是?
Ⅰ
Ⅱ
X轴
·
B
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
·
C
·
A
·
G
·
E
(
2,3
)
(
3,2
)
(
-2,1
)
(
-4,-
3
)
(
1,-
2
)
坐标是有序
数对。
例1、写出图中A、B、C、D、E、F,G,M各点的坐标及所在的象限。
M
(
4,0
)
·
D
(
-4,3
)
·
F
(
-3,-2
)
·
H
(
3,-4
)
你能总结出各象限内点的坐标的符号特点吗?
第一象限:(正,正)
第二象限:(负,正)
第三象限:(负,负)
第四象限:(正,负)
你能说出各个象限内
的特点吗?
1
2
3
-3
x
-2
·
-2
-3
o
-1
y
4
2
5
3
6
1
在如图建立的直角坐标系中描出下列各组点,并将各组点用线段依次连接起来.
做
一
做
①(0
,
6),
(-4,
3),
(4
,
3)
②(-2
,
3),
(-2
,
-3),
(2
,
-3),
(2
,
3)
·
·
·
·
·
·
观察所得的图形,你觉得它象什么?
-4
-1
4
A(-4,3)
B(4,3)
C(-2,3)
D(2,3)
E(-2,-3)
F(2,-3)
(0
,
6)
·
例
2、
A
B
C
D
E
F
例3、写出图中多边形ABCDEF各个顶点的坐标。
(-2,0)
(0,-3)
(3,-3)
(4,0)
(3,3)
(0,3)
例3、观察:(1)点E,F的坐标有什么特点?线段EF与x轴、y轴有什么关系?
(2)点E,C的坐标有什么特点,线段EC与x轴、y轴有什么关系?
(3)x轴上的点的特点;y轴上的点的特点?
结论
纵坐标相同的点的连线平行于x轴
横坐标相同的点的连线平行于y轴
坐标轴上的点至少有一个是0
x轴上的点纵坐标为0,
y轴上的点横坐标为0.
(垂直于y轴)
(垂直于x轴)
你知道吗?
早在1637年以前,法国数学家、解析几何的创始人笛卡尔受到了经纬度的启发,地理上的经纬度是以赤道和本初子午线为标准的,这两条线从局部上可以看成是平面内互相垂直的两条直线。所以笛卡尔的方法是在平面内画两条互相垂直的数轴,其中水平的数轴叫x轴(或横轴),取向右为正方向,铅直的数轴叫y轴(或纵轴),取向上为正方向,它们的交点是原点,这个平面叫坐标平面。
告诉大家
本节课你学会了什么!
小结:
这节课主要学面直角坐标系的有
关概念。掌握:
1.
会根据坐标找点,会由坐标系内的点写坐标
2.x轴,y轴上点的坐标的特点:
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
第一象限:(+,
+)
第二象限:(—,
+)
第三象限:(—,—)
第四象限:(+,
—)
再见
A(6,-2),
B(0,3)
,
C(3,7),
D(-6,-3),
E(-2,0)
,
F(-9,5)
练一练
分别说出下列各点在哪个象限内或在哪条坐标轴上?
第一象限:(正,正)
第二象限:(负,正)
第三象限:(负,负)
第四象限:(正,负)
x轴:纵坐标为0;y轴:横坐标为0
雁塔
中心广场
钟楼
大成殿
科枝大学
碑林
影月湖
如果以“中心广场”为原点作两条相互垂直的数轴,分别取向右和向上的方向为数轴的正方向,一个方格的边长看做一个单位长度,那么你能表示“碑林”的位置吗?“大成殿”的位置呢?
