人教版数学七年级下册课件:5.3.1.1 第1课时 平行线的性质(15张)
文档属性
| 名称 | 人教版数学七年级下册课件:5.3.1.1 第1课时 平行线的性质(15张) |  | |
| 格式 | pptx | ||
| 文件大小 | 748.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 19:59:42 | ||
图片预览


文档简介
第五章 相交线与平行线
5.3.1 平行线的性质
第1课时
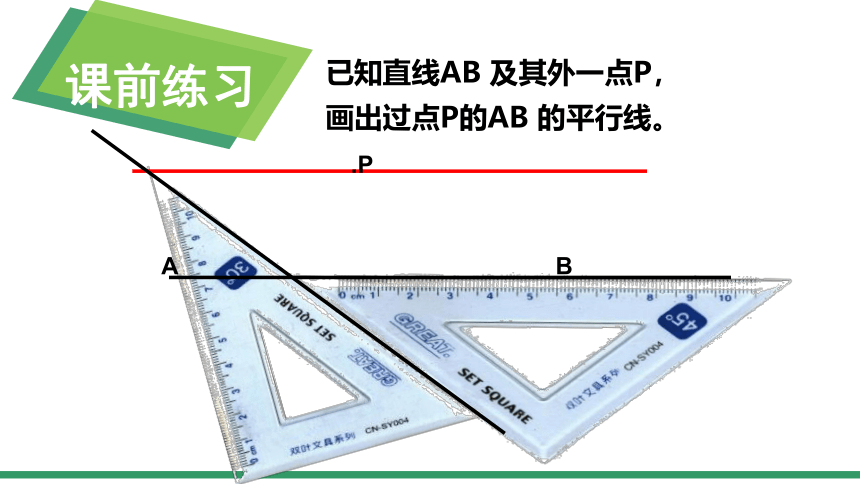
课前练习
已知直线AB 及其外一点P,
画出过点P的AB 的平行线。
A B
.P
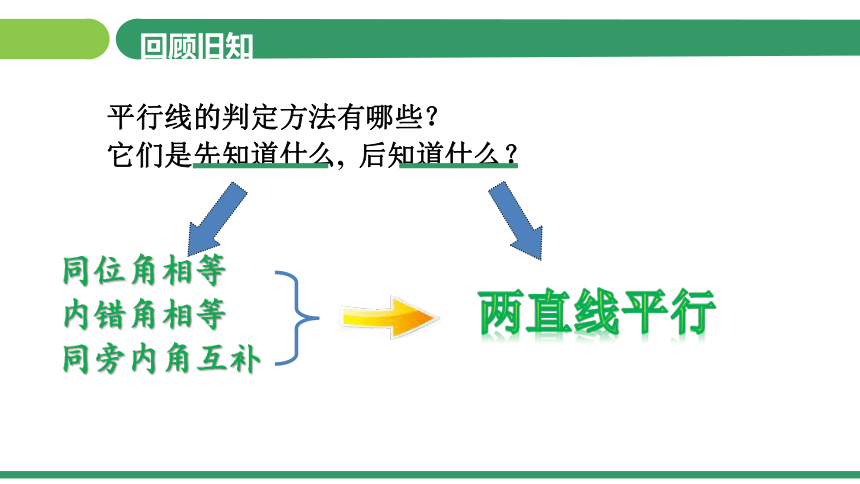
回顾旧知
平行线的判定方法有哪些?
它们是先知道什么, 后知道什么?
同位角相等
内错角相等
同旁内角互补
两直线平行
思考探究
根据同位角相等可以判定两直线平行,
反过来如果两直线平行,同位角之间有什么关系呢?
内错角,同旁内角之间又有什么关系呢?
1
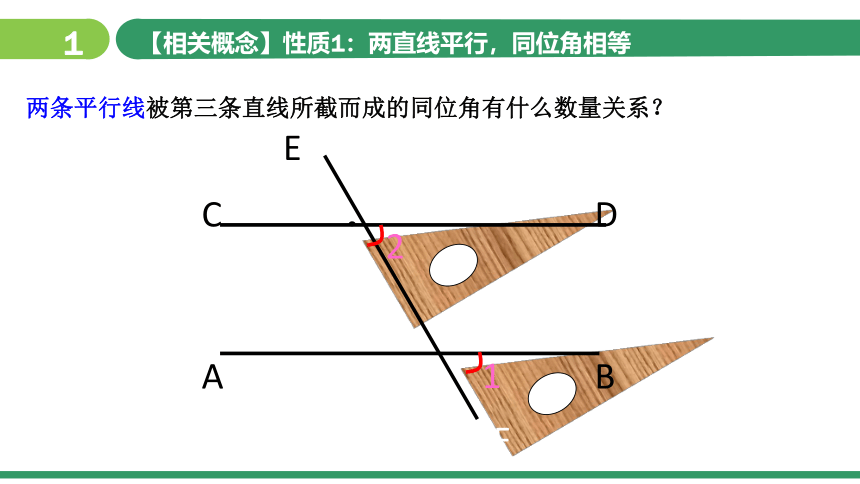
【相关概念】性质1:两直线平行,同位角相等
两条平行线被第三条直线所截而成的同位角有什么数量关系?
A
B
P
C
D
E
F
2
1
1
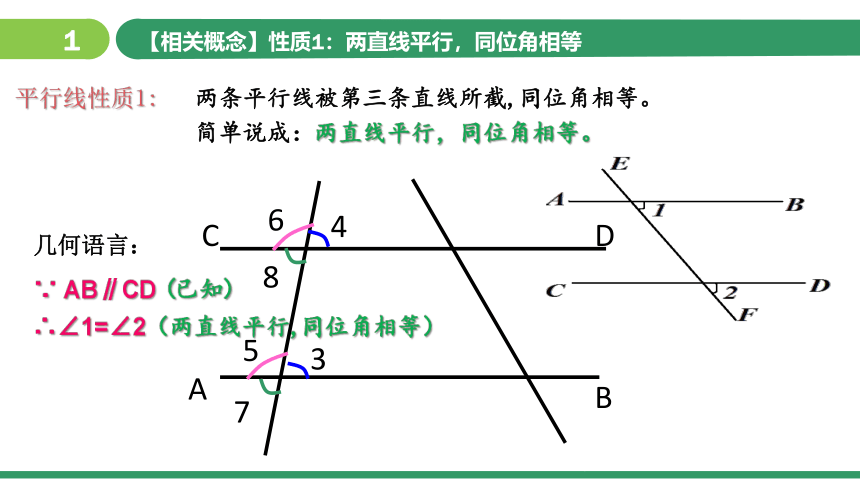
【相关概念】性质1:两直线平行,同位角相等
A
B
C
D
F
2
1
3
4
5
6
8
7
两条平行线被第三条直线所截,同位角相等。
简单说成:两直线平行,同位角相等。
平行线性质1:
几何语言:
∵ AB∥CD (已知)
∴∠1=∠2(两直线平行,同位角相等)
1
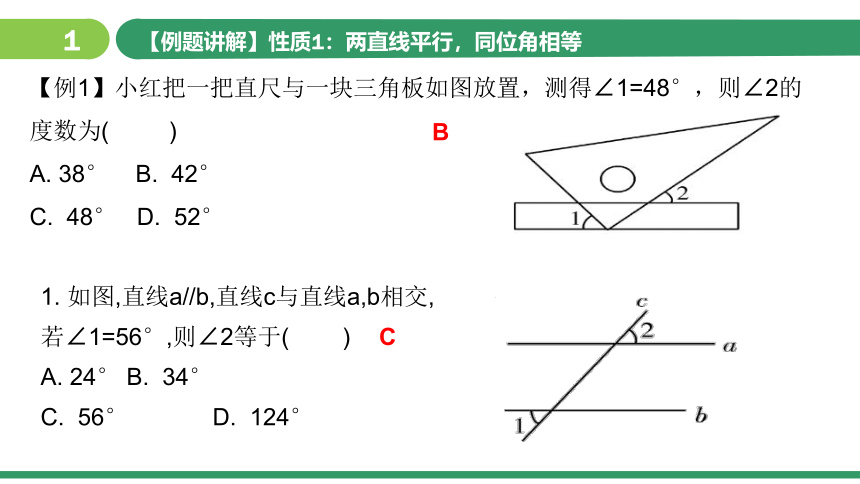
【例题讲解】性质1:两直线平行,同位角相等
【例1】小红把一把直尺与一块三角板如图放置,测得∠1=48°,则∠2的度数为( )
A. 38° B. 42°
C. 48° D. 52°
B
1. 如图,直线a//b,直线c与直线a,b相交,
若∠1=56°,则∠2等于( )
A. 24° B. 34°
C. 56° D. 124°
C
1
【例题讲解】性质1:两直线平行,同位角相等
【例2】如图,a//b,点B在直线b上,
且AB⊥BC,∠1=35°,求∠2的度数.
解: ∵AB⊥BC,∠1=35°(已知),
∴∠3=90°-35°=55°.
∵a//b(已知),
∴∠2=∠3=55°(两直线平行,同位角相等).
3
1
【巩固练习】性质1:两直线平行,同位角相等
2. 如图,∠A=70°,O是AB上一点,直线OD
与AB的夹角∠BOD为80°,要使OD//AC,
直线OD绕点O按逆时针方向至少旋转多少度?
解:∵OD//AC(已知),
∴∠BOD′=∠A=70°(两直线平行,同位角相等).
∴∠DOD′=∠BOD-BOD′=80°-70°=10°.
∴直线OD绕点O按逆时针方向至少旋转10°.
2
【相关概念】性质2:两直线平行,内错角相等
1
2
3
a
b
如图,已知:a// b ,那么∠ 3与∠ 2有什么关系?
例如:∵ a//b,
∴ ∠1= ∠2
(_____________________),
∵ ∠3 = ___(对顶角相等),
∴∠ 2 = ∠3 (__________).
两直线平行,同位角相等
1
等量代换
两条平行线被第三条直线所截,内错角相等。
简单说成:两直线平行,内错角相等。
平行线性质2:
几何语言:
∵ AB∥CD (已知)
∴∠2=∠3(两直线平行,内错角相等)
2
【例题讲解】性质2:两直线平行,内错角相等
【例3】如图所示,直线a,b被直线c,d所截.
若∠1=80°,∠2=100°,∠3=85°,
则∠4度数是( )
A. 80 B. 85° C. 95° D. 100°
B
3. 将直尺和直角三角板按如图方式摆放,
已知∠1=30°,则∠2的大小是( )
A. 30° B. 45°
C. 60° D. 65°
C
2
【例题讲解】性质2:两直线平行,内错角相等
【例4】已知直线m//n,将一块含30°角的直角三角板ABC按如图方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上,若∠1=20°,求∠2的度数.
解:∵m//n(已知),
∴∠2=∠1+∠3
(两直线平行,内错角相等).
∵∠1=20°,∠3=30°,
∴∠2=50°.
3
解:∵AB//CD(已知),
∴∠ABC=∠C=32°(两直线平行,内错角相等).
又∵BC平分∠ABE(已知),
∴∠ABE=2∠ABC=64°(角平分线的性质).
∴∠BED=∠ABE=64°
(两直线平行,内错角相等).
2
【巩固练习】性质2:两直线平行,内错角相等
4. 如图,已知AB//CD,BC平分∠ABE,
∠C=32°,求∠BED的度数.
课堂小结
两直线平行,同位角相等
平行线性质1:
两直线平行,内错角相等
平行线性质2:
1. P2 5.2.2
2.《学导练》P24-P5
3.《课堂10分钟》P121-P122
作业:
5.3.1 平行线的性质
第1课时
课前练习
已知直线AB 及其外一点P,
画出过点P的AB 的平行线。
A B
.P
回顾旧知
平行线的判定方法有哪些?
它们是先知道什么, 后知道什么?
同位角相等
内错角相等
同旁内角互补
两直线平行
思考探究
根据同位角相等可以判定两直线平行,
反过来如果两直线平行,同位角之间有什么关系呢?
内错角,同旁内角之间又有什么关系呢?
1
【相关概念】性质1:两直线平行,同位角相等
两条平行线被第三条直线所截而成的同位角有什么数量关系?
A
B
P
C
D
E
F
2
1
1
【相关概念】性质1:两直线平行,同位角相等
A
B
C
D
F
2
1
3
4
5
6
8
7
两条平行线被第三条直线所截,同位角相等。
简单说成:两直线平行,同位角相等。
平行线性质1:
几何语言:
∵ AB∥CD (已知)
∴∠1=∠2(两直线平行,同位角相等)
1
【例题讲解】性质1:两直线平行,同位角相等
【例1】小红把一把直尺与一块三角板如图放置,测得∠1=48°,则∠2的度数为( )
A. 38° B. 42°
C. 48° D. 52°
B
1. 如图,直线a//b,直线c与直线a,b相交,
若∠1=56°,则∠2等于( )
A. 24° B. 34°
C. 56° D. 124°
C
1
【例题讲解】性质1:两直线平行,同位角相等
【例2】如图,a//b,点B在直线b上,
且AB⊥BC,∠1=35°,求∠2的度数.
解: ∵AB⊥BC,∠1=35°(已知),
∴∠3=90°-35°=55°.
∵a//b(已知),
∴∠2=∠3=55°(两直线平行,同位角相等).
3
1
【巩固练习】性质1:两直线平行,同位角相等
2. 如图,∠A=70°,O是AB上一点,直线OD
与AB的夹角∠BOD为80°,要使OD//AC,
直线OD绕点O按逆时针方向至少旋转多少度?
解:∵OD//AC(已知),
∴∠BOD′=∠A=70°(两直线平行,同位角相等).
∴∠DOD′=∠BOD-BOD′=80°-70°=10°.
∴直线OD绕点O按逆时针方向至少旋转10°.
2
【相关概念】性质2:两直线平行,内错角相等
1
2
3
a
b
如图,已知:a// b ,那么∠ 3与∠ 2有什么关系?
例如:∵ a//b,
∴ ∠1= ∠2
(_____________________),
∵ ∠3 = ___(对顶角相等),
∴∠ 2 = ∠3 (__________).
两直线平行,同位角相等
1
等量代换
两条平行线被第三条直线所截,内错角相等。
简单说成:两直线平行,内错角相等。
平行线性质2:
几何语言:
∵ AB∥CD (已知)
∴∠2=∠3(两直线平行,内错角相等)
2
【例题讲解】性质2:两直线平行,内错角相等
【例3】如图所示,直线a,b被直线c,d所截.
若∠1=80°,∠2=100°,∠3=85°,
则∠4度数是( )
A. 80 B. 85° C. 95° D. 100°
B
3. 将直尺和直角三角板按如图方式摆放,
已知∠1=30°,则∠2的大小是( )
A. 30° B. 45°
C. 60° D. 65°
C
2
【例题讲解】性质2:两直线平行,内错角相等
【例4】已知直线m//n,将一块含30°角的直角三角板ABC按如图方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上,若∠1=20°,求∠2的度数.
解:∵m//n(已知),
∴∠2=∠1+∠3
(两直线平行,内错角相等).
∵∠1=20°,∠3=30°,
∴∠2=50°.
3
解:∵AB//CD(已知),
∴∠ABC=∠C=32°(两直线平行,内错角相等).
又∵BC平分∠ABE(已知),
∴∠ABE=2∠ABC=64°(角平分线的性质).
∴∠BED=∠ABE=64°
(两直线平行,内错角相等).
2
【巩固练习】性质2:两直线平行,内错角相等
4. 如图,已知AB//CD,BC平分∠ABE,
∠C=32°,求∠BED的度数.
课堂小结
两直线平行,同位角相等
平行线性质1:
两直线平行,内错角相等
平行线性质2:
1. P2 5.2.2
2.《学导练》P24-P5
3.《课堂10分钟》P121-P122
作业:
