人教版七年级数学下册课件:9.2 第2课时 一元一次不等式的应用(16张)
文档属性
| 名称 | 人教版七年级数学下册课件:9.2 第2课时 一元一次不等式的应用(16张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 19:59:44 | ||
图片预览





文档简介
第九章 不等式与不等式组
9.2 第2课时 一元一次不等式的应用
知识回顾
1.一元一次不等式的解法:
其一般步骤:(1)去分母;(2)去括号;(3)移项;
(4)合并同类项;(5)系数化为1(注意不等号方向是否改变)
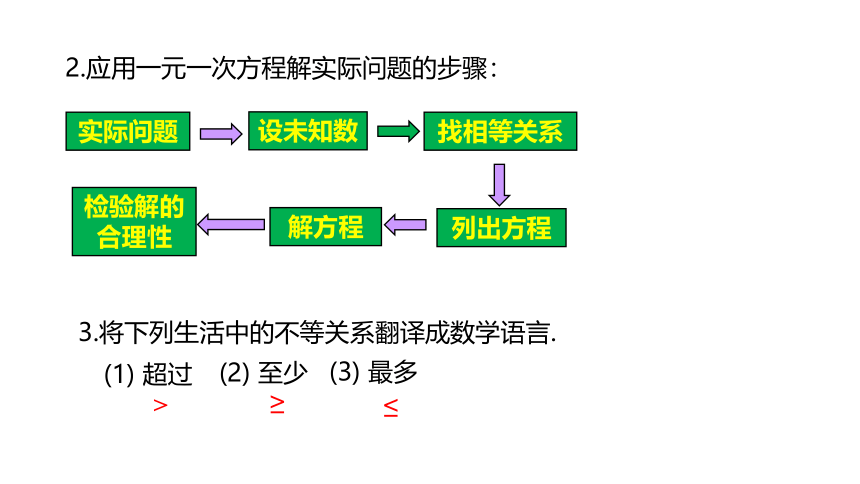
解一元一次不等式,就是要根据不等式的性质,将不等式逐步化为x>a(x≥a)或x2.应用一元一次方程解实际问题的步骤:
实际问题
找相等关系
设未知数
列出方程
检验解的合理性
解方程
3.将下列生活中的不等关系翻译成数学语言.
(1) 超过
(2) 至少
(3) 最多
>
≥
≤
例题讲解
列一元一次不等式解应用题的基本步骤与列一元一次方程解应用题的步骤相类似.
有些实际问题中,存在不等关系,用不等式来表示这样的关系,就能把实际问题转化为数学问题,从而通过解不等式得到实际问题的答案.
例1 去年某市空气质量良好(二级以上)的天数与全年天数(365)之比达到60%,如果明年(365天)这样的比值要超过70%,那么明年空气质量良好的天数比去年至少要增加多少?
分析:“明年这样的比值要超过70%”指出了这个
问题中蕴含的不等关系,转化为不等式,即
>70%.
明年空气质量好的天数
明年天数
解: 设明年比去年空气质量良好的天数增加x天.
解得 x>36.5.
答:明年空气质量良好的天数比去年至少要增加37天,才能使这一年空气质量良好的天数超过全年天数的70%.
由x 应为正整数,得 x≥37.
>70%.
x+365×60%
365
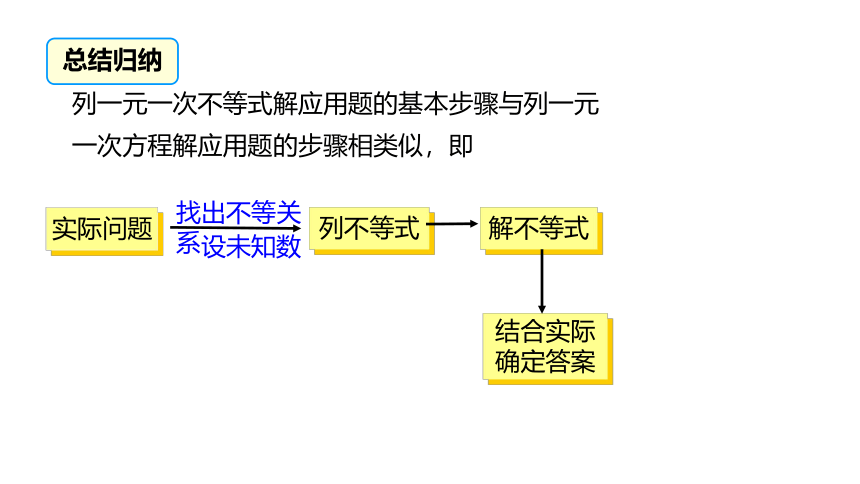
列一元一次不等式解应用题的基本步骤与列一元一次方程解应用题的步骤相类似,即
实际问题
解不等式
列不等式
结合实际
确定答案
找出不等关系
设未知数
总结归纳
例2 甲、乙两超市以同样价格出售同样的商品,并且给出了不同的优惠方案:在甲超市累计购物超过100元后,超出100元的部分按90%收费;在乙超市累计购物超过50元后,超出50元的部分按95%收费,顾客到哪家超市购物花费少?
分析:甲、乙两超市的优惠价格不一样,因此需要分类讨论:
(1)当购物不超过50元;
(2)当购物超过50元而不超过100元;
(3)当购物超过100元.
解:(1)当购物不超过50元时,在甲、乙两超市都不享受优惠,购物花费一样;
(2)当购物超过50元而不超过100元时,在乙超市享受优惠, 购物花费少;
(3)当累计购物超过100元后,设购物为x(x>100)元:
①若50+0.95(x-50)>100+0.9(x-100), 即x>150, 在甲超市购物花费少;
②若50+0.95(x-50)<100+0.9(x-100), 即x<150,在乙超市购物花费少;
③若50+0.95(x-50)=100+0.9(x-100) ,即x=150,在甲、乙两超市购物花费一样.
随堂演练
1. 某汽车租赁公司要购买轿车和面包车共10辆,其中轿车至少要购买3辆,轿车每辆7万元,面包车每辆4万元,公司可投入的购车款不超过55万元.符合公司要求的购买方案有哪几种?
解:设要购买轿车x辆,则要购买面包车(10-x)辆.
由题意得7x+4(10-x)≤55,解得x≤5.
又因为x≥3,且x为整数,所以x=3,4,5.
因此有三种购买方案:①购买轿车3辆,面包车7辆;
②购买轿车4辆,面包车6辆;③购买轿车5辆,面包车5辆.
2. 一辆货车向灾区运送物资,共有80千米的路程,需要1小时送到,前半小时已经走了30千米,后半小时的速度至少为多少才能不延误时间?
解:设后半小时的速度为x千米/时.根据题意,得
0.5x≥80-30,
解得x≥100.
答:后半小时的速度至少为100千米/时才能不延误时间.
3.某篮球联赛初赛阶段,每队有10场比赛,每场比赛都要分出胜负,每
队胜一场得2分,负一场得1分,积分超过15分才能获得参加决赛的资格.
(1)已知甲队在初赛阶段积分为18分,求甲队初赛阶段胜、负各多少场;
(2)如果乙队要获得参加决赛资格,那么乙队在初赛阶段至少要胜多少场?
解:(1)设甲队初赛阶段胜x场,则负(10-x)场.
根据题意,得2x+(10-x)=18,
解得x=8.
则10-x=2.
答:甲队初赛阶段胜8场,负2场.
(2)设乙队在初赛阶段胜a场.
根据题意,得2a+(10-a)>15,
解得a>5.
因为a为非负整数,
所以a至少为6.
答:乙队在初赛阶段至少要胜6场.
4.某校一名老师将在假期带领学生去北京旅游,有两种购票方式:
甲旅行社说:“如果老师买全票,其他人全部半价优惠.”乙旅行社
说:“所有人按全票价的6折优惠.”已知全票价240元.设学生有x名
,甲旅行社的收费为y1元,乙旅行社的收费为y2元.
(1)分别表示两家旅行社的收费y1,y2与x的关系式;
(2)就学生人数讨论哪家旅行社更优惠.
解:(1)y1=240+240×50%×x=240+120x;
y2=240×60%×(x+1)=144(x+1)=144x+144.
(2)若y1=y2,则240+120x=144x+144,解得x=4,
此时两家旅行社收费一样;
若y1>y2,则240+120x>144x+144,解得x<4,
此时乙旅行社更优惠;
若y14,
此时甲旅行社更优惠.
课堂小结
一元一次不等式的应用
实际问题
↓
根据题意列不等式
↓
解一元一次不等式
→
→
根据实际问题找出符合条件的解集或整数解
↑
得出解决问题的答案
9.2 第2课时 一元一次不等式的应用
知识回顾
1.一元一次不等式的解法:
其一般步骤:(1)去分母;(2)去括号;(3)移项;
(4)合并同类项;(5)系数化为1(注意不等号方向是否改变)
解一元一次不等式,就是要根据不等式的性质,将不等式逐步化为x>a(x≥a)或x
实际问题
找相等关系
设未知数
列出方程
检验解的合理性
解方程
3.将下列生活中的不等关系翻译成数学语言.
(1) 超过
(2) 至少
(3) 最多
>
≥
≤
例题讲解
列一元一次不等式解应用题的基本步骤与列一元一次方程解应用题的步骤相类似.
有些实际问题中,存在不等关系,用不等式来表示这样的关系,就能把实际问题转化为数学问题,从而通过解不等式得到实际问题的答案.
例1 去年某市空气质量良好(二级以上)的天数与全年天数(365)之比达到60%,如果明年(365天)这样的比值要超过70%,那么明年空气质量良好的天数比去年至少要增加多少?
分析:“明年这样的比值要超过70%”指出了这个
问题中蕴含的不等关系,转化为不等式,即
>70%.
明年空气质量好的天数
明年天数
解: 设明年比去年空气质量良好的天数增加x天.
解得 x>36.5.
答:明年空气质量良好的天数比去年至少要增加37天,才能使这一年空气质量良好的天数超过全年天数的70%.
由x 应为正整数,得 x≥37.
>70%.
x+365×60%
365
列一元一次不等式解应用题的基本步骤与列一元一次方程解应用题的步骤相类似,即
实际问题
解不等式
列不等式
结合实际
确定答案
找出不等关系
设未知数
总结归纳
例2 甲、乙两超市以同样价格出售同样的商品,并且给出了不同的优惠方案:在甲超市累计购物超过100元后,超出100元的部分按90%收费;在乙超市累计购物超过50元后,超出50元的部分按95%收费,顾客到哪家超市购物花费少?
分析:甲、乙两超市的优惠价格不一样,因此需要分类讨论:
(1)当购物不超过50元;
(2)当购物超过50元而不超过100元;
(3)当购物超过100元.
解:(1)当购物不超过50元时,在甲、乙两超市都不享受优惠,购物花费一样;
(2)当购物超过50元而不超过100元时,在乙超市享受优惠, 购物花费少;
(3)当累计购物超过100元后,设购物为x(x>100)元:
①若50+0.95(x-50)>100+0.9(x-100), 即x>150, 在甲超市购物花费少;
②若50+0.95(x-50)<100+0.9(x-100), 即x<150,在乙超市购物花费少;
③若50+0.95(x-50)=100+0.9(x-100) ,即x=150,在甲、乙两超市购物花费一样.
随堂演练
1. 某汽车租赁公司要购买轿车和面包车共10辆,其中轿车至少要购买3辆,轿车每辆7万元,面包车每辆4万元,公司可投入的购车款不超过55万元.符合公司要求的购买方案有哪几种?
解:设要购买轿车x辆,则要购买面包车(10-x)辆.
由题意得7x+4(10-x)≤55,解得x≤5.
又因为x≥3,且x为整数,所以x=3,4,5.
因此有三种购买方案:①购买轿车3辆,面包车7辆;
②购买轿车4辆,面包车6辆;③购买轿车5辆,面包车5辆.
2. 一辆货车向灾区运送物资,共有80千米的路程,需要1小时送到,前半小时已经走了30千米,后半小时的速度至少为多少才能不延误时间?
解:设后半小时的速度为x千米/时.根据题意,得
0.5x≥80-30,
解得x≥100.
答:后半小时的速度至少为100千米/时才能不延误时间.
3.某篮球联赛初赛阶段,每队有10场比赛,每场比赛都要分出胜负,每
队胜一场得2分,负一场得1分,积分超过15分才能获得参加决赛的资格.
(1)已知甲队在初赛阶段积分为18分,求甲队初赛阶段胜、负各多少场;
(2)如果乙队要获得参加决赛资格,那么乙队在初赛阶段至少要胜多少场?
解:(1)设甲队初赛阶段胜x场,则负(10-x)场.
根据题意,得2x+(10-x)=18,
解得x=8.
则10-x=2.
答:甲队初赛阶段胜8场,负2场.
(2)设乙队在初赛阶段胜a场.
根据题意,得2a+(10-a)>15,
解得a>5.
因为a为非负整数,
所以a至少为6.
答:乙队在初赛阶段至少要胜6场.
4.某校一名老师将在假期带领学生去北京旅游,有两种购票方式:
甲旅行社说:“如果老师买全票,其他人全部半价优惠.”乙旅行社
说:“所有人按全票价的6折优惠.”已知全票价240元.设学生有x名
,甲旅行社的收费为y1元,乙旅行社的收费为y2元.
(1)分别表示两家旅行社的收费y1,y2与x的关系式;
(2)就学生人数讨论哪家旅行社更优惠.
解:(1)y1=240+240×50%×x=240+120x;
y2=240×60%×(x+1)=144(x+1)=144x+144.
(2)若y1=y2,则240+120x=144x+144,解得x=4,
此时两家旅行社收费一样;
若y1>y2,则240+120x>144x+144,解得x<4,
此时乙旅行社更优惠;
若y1
此时甲旅行社更优惠.
课堂小结
一元一次不等式的应用
实际问题
↓
根据题意列不等式
↓
解一元一次不等式
→
→
根据实际问题找出符合条件的解集或整数解
↑
得出解决问题的答案
