甘肃省兰州市第四片区2020-2021学年高一上学期期末考试数学试题 Word版含答案
文档属性
| 名称 | 甘肃省兰州市第四片区2020-2021学年高一上学期期末考试数学试题 Word版含答案 |  | |
| 格式 | doc | ||
| 文件大小 | 751.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 20:02:49 | ||
图片预览




文档简介
兰州市第四片区2020—2021学年第一学期联片办学期末考试
高一年级 数学学科
(满分150分 ,考试时间120分钟)
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息;
2.请将答案正确填写在答题卡上对应区域,答在试卷上不得分.
一、选择题(本大题共12小题,每小题5分,共60分,只有一项符合题目要求,请将答案填入答题卡内。)
1.设全集为,集合,,(? )
A. B. C. D.
2.下列函数中,既是奇函数又在定义域上是增函数的为(? )
A. B. C. D.
3.若经过A(3,m),B(1,2)两点的直线的倾斜角为45°,则m=( )
A.4 B.-6 C.6 D.-4
4.函数的零点所在的一个区间是( )
A. B. C. D.
5. ,是空间两条不同的直线,,是两个不同的平面,则下列命题中正确的是(??)
A.若?,,?,则
B.若?,, ,则
C.若?,,?,则
D.若?,, ,则
6.某几何体的三视图如图所示(其中俯视图中的曲线是圆弧),则该几何体的表面积为( )
B.
C. D.
7.函数y=\log2x\-的零点个数是( )
A.0 B.2 C.1 D.3
8.用与球心距离为1的平面去截球,所得截面面积为π,则球的体积为( )
A. B. C.8π D.
9.在△ABC中,,若使绕直线旋转一周,则所形成的几何体的体积是( )
A. B. C. D.
10. 如图,在正方体中,直线与平面所成的角的大小是( )
A. B. C. D.
11.直三棱柱ABC-A1B1C1中,若∠BAC=90°,AB=AC=AA1,则异面直线BA1与AC1所成的角等于( )
A.30° B.45° C.60° D.90°
12.已知正四棱锥的底面是边长为4的正方形,若一个半径为1的球与此四棱锥所有面都相切,则该四棱锥的高是( )
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,共20分,请将答案填入答题卡内.)
13.若三个球的表面积之比是,则它们的体积之比是_____________.
14.正方体 中,是上底面中心,若正方体的棱长为,
则三棱锥的体积为____________.
15.已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为_______.
16.已知定义在R上的奇函数f(x),当x∈(0,+∞)时,f(x)=log2x,则不等式f(x)<-1的解集是 .?
三.解答题(本大题共6小题,共70分,解答应写出必要的文字说明、证明过程或演算步骤,请将答案填入答题卡内.)
17. (10分)已知:函数,
(1)求函数的定义域;判断函数的奇偶性并说明理由;
(2)判断函数在上的单调性,并用定义加以证明.
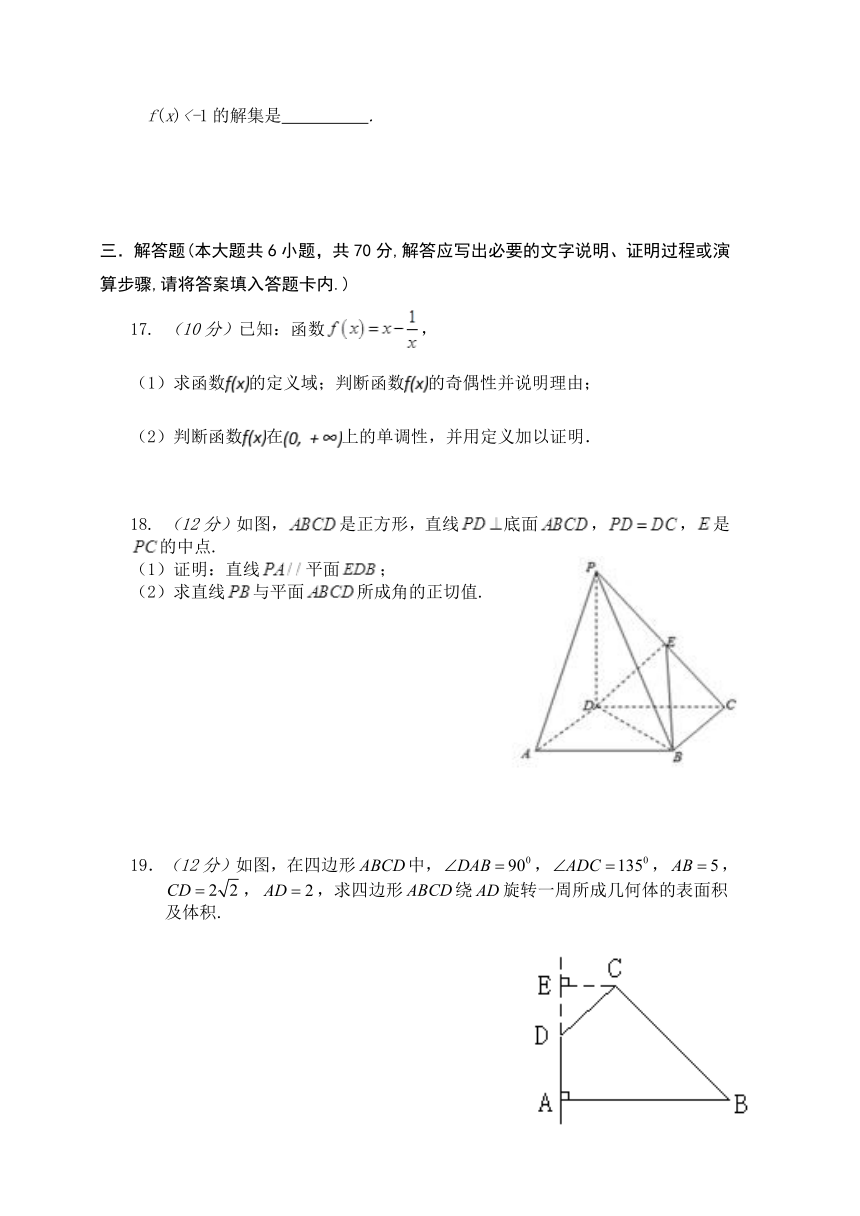
18. (12分)如图,是正方形,直线底面,,是的中点.
(1)证明:直线平面;
(2)求直线与平面所成角的正切值.
19.(12分)如图,在四边形中,,,,,,求四边形绕旋转一周所成几何体的表面积及体积.
20.(12分) 已知幂函数在为减函数,且对数函数满足
(1)求、的解析式
(2)若实数满足,求实数的取值范围.
21. (12分)如图,在三棱锥-中,⊥,⊥,⊥,,为线段的中点,为线段上一点.?
求证:;? 求证:平面⊥平面;
当//平面时,求三棱锥的体积.
22.(12分)如图:在四棱锥V-ABCD中,底面ABCD是边长为2的正方形,其它四个侧面都是侧棱长为的等腰三角形.
求二面角V-AB-C的平面角的大小;
(2)求四棱锥V-ABCD的体积.
2020—2021学年第一学期联片办学期末考试
高一数学参考答案
1 2 3 4 5 6 7 8 9 10 11 12
答案 D D A B D A B D D D C B
14.
16. (-∞,-2)∪
17解:(1)定义域:,定义域关于原点对称,
函数是奇函数;(5分)
(2)判断:函数在上是增函数,
证明:任取
,
因为
函数在上是增函数.(10分)
18.解:(1)连接,交于○,连接
四边形为正方形○为中点,又为中点
:平面平面平面(6分)
(2):平面直线与平面所成角即为
:.
设,则(12分)
19解:S表面=S下底面+S台侧面+S锥侧面
=π×52+π×(2+5)×5+π×2×2
=(60+4)π.(6分)
。.........................................(12分)
20.解:(1)幂函数在为减函数,
∴ ,
解得,
∴ ;
又∵ 是对数函数,且,
∴ 设且,
∴ ,
即,
解得,
∴ ;(6分)
(2)∵ 实数满足,
且在上单调递增,
∴ ,
解得;
即,
∴ 实数的取值范围是.(12分)
21.证明:由,,
平面,平面,
且,
可得平面,
由平面,
可得.?(4分)
证明:由,为线段的中点,
可得,
由平面,平面,
可得平面平面,
又平面平面,
平面,且,
即有平面,
平面,
可得平面平面.?(8分)
解:由平面,平面,
且平面平面,
可得,
又为的中点,
可得为的中点,且,
由平面,
可得平面,
可得,
则三棱锥的体积为:
.(12分)? ? 22.解(1)取AB的中点M,CD的中点N,连MN、VM、VN,
∵底面ABCD是边长为2的正方形,∴MN⊥AB,MN=2???????
又∵VA=VB=,M为AB的中点,∴VM⊥AB?????????????
∴∠VMN是二面角V-AB-C的平面角?
在Rt△VAM中,AM=1,VA=,
∴VM==2,同理可得VN=2?????????? ?
∴△VMN是正三角形,可得∠VMN=60°
即二面角V-AB-C的大小为60°?????????????(6分)
(2)由(1)知AB⊥平面VMN??????????
∵AB?平面ABCD,∴平面ABCD⊥平面VMN??????????
过V作VO⊥MN于点O,
∵平面ABCD⊥平面VMN,平面ABCD∩平面VMN=MN,VO?平面VMN
∴VO⊥平面ABCD,得VO是四棱锥V-ABCD的高?????
∵VM=MN=NV=2,∴VO=????????????????????
因此,四棱锥V-ABCD的体积为
V=SABCD×VO==??????(12分)
高一年级 数学学科
(满分150分 ,考试时间120分钟)
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息;
2.请将答案正确填写在答题卡上对应区域,答在试卷上不得分.
一、选择题(本大题共12小题,每小题5分,共60分,只有一项符合题目要求,请将答案填入答题卡内。)
1.设全集为,集合,,(? )
A. B. C. D.
2.下列函数中,既是奇函数又在定义域上是增函数的为(? )
A. B. C. D.
3.若经过A(3,m),B(1,2)两点的直线的倾斜角为45°,则m=( )
A.4 B.-6 C.6 D.-4
4.函数的零点所在的一个区间是( )
A. B. C. D.
5. ,是空间两条不同的直线,,是两个不同的平面,则下列命题中正确的是(??)
A.若?,,?,则
B.若?,, ,则
C.若?,,?,则
D.若?,, ,则
6.某几何体的三视图如图所示(其中俯视图中的曲线是圆弧),则该几何体的表面积为( )
B.
C. D.
7.函数y=\log2x\-的零点个数是( )
A.0 B.2 C.1 D.3
8.用与球心距离为1的平面去截球,所得截面面积为π,则球的体积为( )
A. B. C.8π D.
9.在△ABC中,,若使绕直线旋转一周,则所形成的几何体的体积是( )
A. B. C. D.
10. 如图,在正方体中,直线与平面所成的角的大小是( )
A. B. C. D.
11.直三棱柱ABC-A1B1C1中,若∠BAC=90°,AB=AC=AA1,则异面直线BA1与AC1所成的角等于( )
A.30° B.45° C.60° D.90°
12.已知正四棱锥的底面是边长为4的正方形,若一个半径为1的球与此四棱锥所有面都相切,则该四棱锥的高是( )
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,共20分,请将答案填入答题卡内.)
13.若三个球的表面积之比是,则它们的体积之比是_____________.
14.正方体 中,是上底面中心,若正方体的棱长为,
则三棱锥的体积为____________.
15.已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为_______.
16.已知定义在R上的奇函数f(x),当x∈(0,+∞)时,f(x)=log2x,则不等式f(x)<-1的解集是 .?
三.解答题(本大题共6小题,共70分,解答应写出必要的文字说明、证明过程或演算步骤,请将答案填入答题卡内.)
17. (10分)已知:函数,
(1)求函数的定义域;判断函数的奇偶性并说明理由;
(2)判断函数在上的单调性,并用定义加以证明.
18. (12分)如图,是正方形,直线底面,,是的中点.
(1)证明:直线平面;
(2)求直线与平面所成角的正切值.
19.(12分)如图,在四边形中,,,,,,求四边形绕旋转一周所成几何体的表面积及体积.
20.(12分) 已知幂函数在为减函数,且对数函数满足
(1)求、的解析式
(2)若实数满足,求实数的取值范围.
21. (12分)如图,在三棱锥-中,⊥,⊥,⊥,,为线段的中点,为线段上一点.?
求证:;? 求证:平面⊥平面;
当//平面时,求三棱锥的体积.
22.(12分)如图:在四棱锥V-ABCD中,底面ABCD是边长为2的正方形,其它四个侧面都是侧棱长为的等腰三角形.
求二面角V-AB-C的平面角的大小;
(2)求四棱锥V-ABCD的体积.
2020—2021学年第一学期联片办学期末考试
高一数学参考答案
1 2 3 4 5 6 7 8 9 10 11 12
答案 D D A B D A B D D D C B
14.
16. (-∞,-2)∪
17解:(1)定义域:,定义域关于原点对称,
函数是奇函数;(5分)
(2)判断:函数在上是增函数,
证明:任取
,
因为
函数在上是增函数.(10分)
18.解:(1)连接,交于○,连接
四边形为正方形○为中点,又为中点
:平面平面平面(6分)
(2):平面直线与平面所成角即为
:.
设,则(12分)
19解:S表面=S下底面+S台侧面+S锥侧面
=π×52+π×(2+5)×5+π×2×2
=(60+4)π.(6分)
。.........................................(12分)
20.解:(1)幂函数在为减函数,
∴ ,
解得,
∴ ;
又∵ 是对数函数,且,
∴ 设且,
∴ ,
即,
解得,
∴ ;(6分)
(2)∵ 实数满足,
且在上单调递增,
∴ ,
解得;
即,
∴ 实数的取值范围是.(12分)
21.证明:由,,
平面,平面,
且,
可得平面,
由平面,
可得.?(4分)
证明:由,为线段的中点,
可得,
由平面,平面,
可得平面平面,
又平面平面,
平面,且,
即有平面,
平面,
可得平面平面.?(8分)
解:由平面,平面,
且平面平面,
可得,
又为的中点,
可得为的中点,且,
由平面,
可得平面,
可得,
则三棱锥的体积为:
.(12分)? ? 22.解(1)取AB的中点M,CD的中点N,连MN、VM、VN,
∵底面ABCD是边长为2的正方形,∴MN⊥AB,MN=2???????
又∵VA=VB=,M为AB的中点,∴VM⊥AB?????????????
∴∠VMN是二面角V-AB-C的平面角?
在Rt△VAM中,AM=1,VA=,
∴VM==2,同理可得VN=2?????????? ?
∴△VMN是正三角形,可得∠VMN=60°
即二面角V-AB-C的大小为60°?????????????(6分)
(2)由(1)知AB⊥平面VMN??????????
∵AB?平面ABCD,∴平面ABCD⊥平面VMN??????????
过V作VO⊥MN于点O,
∵平面ABCD⊥平面VMN,平面ABCD∩平面VMN=MN,VO?平面VMN
∴VO⊥平面ABCD,得VO是四棱锥V-ABCD的高?????
∵VM=MN=NV=2,∴VO=????????????????????
因此,四棱锥V-ABCD的体积为
V=SABCD×VO==??????(12分)
同课章节目录
