青岛版八年级数学上册1.2 怎样判定三角形全等-同步练习(word版含答案)
文档属性
| 名称 | 青岛版八年级数学上册1.2 怎样判定三角形全等-同步练习(word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 205.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 12:38:12 | ||
图片预览



文档简介
1.2
怎样判定三角形全等
基础过关
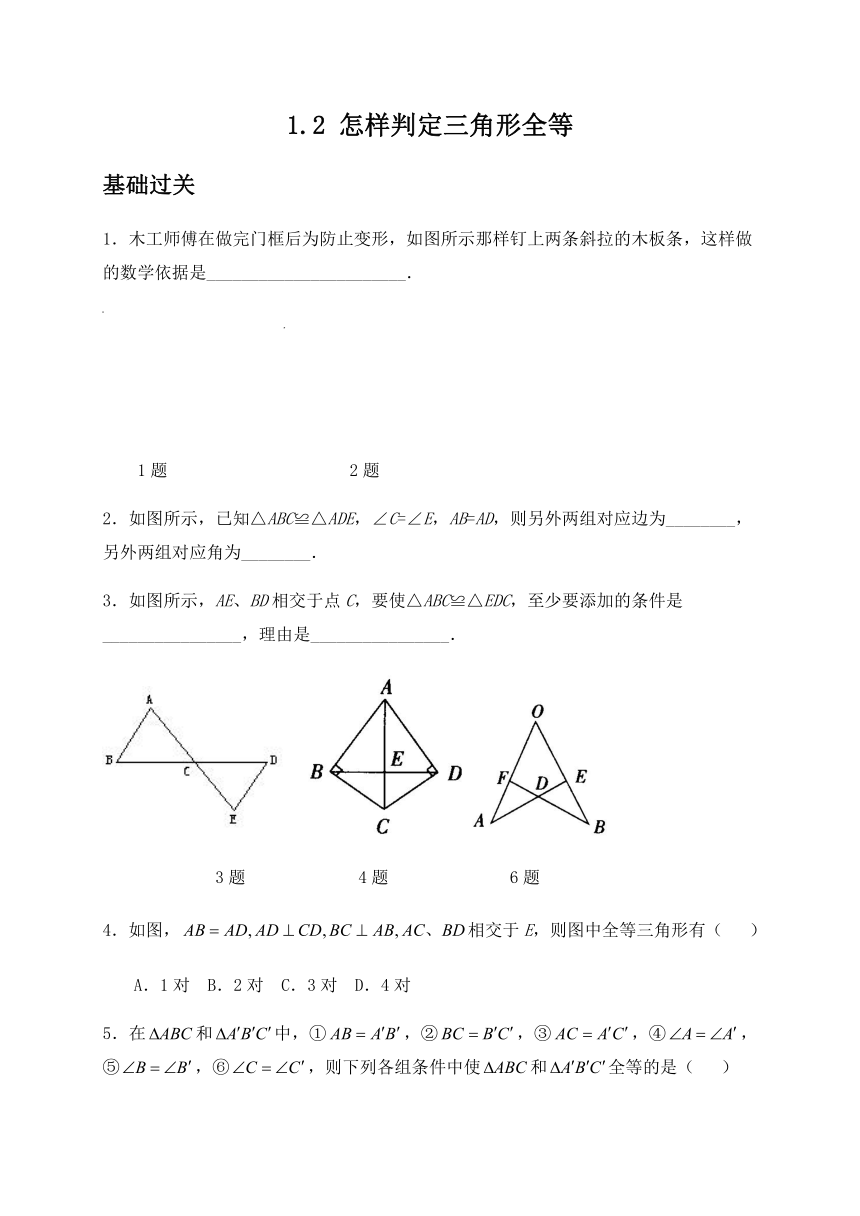
1.木工师傅在做完门框后为防止变形,如图所示那样钉上两条斜拉的木板条,这样做的数学依据是_______________________.
1题
2题
2.如图所示,已知△ABC≌△ADE,∠C=∠E,AB=AD,则另外两组对应边为________,另外两组对应角为________.
3.如图所示,AE、BD相交于点C,要使△ABC≌△EDC,至少要添加的条件是________________,理由是________________.
3题
4题
6题
4.如图,相交于E,则图中全等三角形有(
)
A.1对
B.2对
C.3对
D.4对
5.在和中,①,②,③,④,⑤,⑥,则下列各组条件中使和全等的是(
)
A.④⑤⑥
B.①②⑥
C.①③⑤
D.②⑤⑥
6.如图,已知和BF交于点D,①≌;②≌,③D在的平分线上,则以上结论中正确的是(
)
A.只有①
B.只有①②
C.有①②③
D.①和③
能力提升
7.如图,在中,为BC边中点,那么以下结论不正确的是(
)
A.≌
B.
C.AD平分
D.是等边三角形
7题
8题
8.如图,,则(
)
A.45°
B.55°
C.35°
D.65°
9.已知:如图,AB与DC相交于点,若使≌,则(
)
A.应补充条件
B.应补充条件
C.不用补充条件
D.以上说法都不正确
9题
10题
10.如图,已知,则图中全等三角形的总对数是(
)
A.3
B.4
C.5
D.6
11.如图所示,∠ABC=∠DEF,AB=DE,要说明△ABC≌△DEF.
(1)若以“SAS”为依据,还需添加的一个条件是
;
(2)若以“ASA”为依据,还需添加的一个条件是
;
(3)符以“AAS”为依据,还需添加的一个条件是
.
11题
12题
12.如图所示,∠C=∠D=90°,清你添加一个条件,使得△ABC≌△BAD,并在添加的每一个条件后的括号内,写出添加这个条件后判定三角形全等的理由.
(1)
(
):
(2)
(
);
(3)
(
):
(4)
(
).
应用拓展
13.如图所示,CD⊥AB于点D,BE⊥AC于点E,BE,CD交于点O,且AO平分∠BAC.求证OB=OC.
14.如图,AB=AC,BD=CD,求证:∠1=∠2.
15.如图,已知AB=CD,AC=BD,求证:∠A=∠D.
16.如图,AC与BD交于点O,AD=CB,E、F是BD上两点,且AE=CF,DE=BF.请推导下列结论:
⑴∠D=∠B;⑵AE∥CF.
创新突破
17.如图,已知的交点是E,并且与相等吗?试说明你的答案.
18.如图:已知,,那么≌吗?
19.如图,D是的边AB上一点,DF交AC于点,那么吗?
答案
三角形的稳定性
BC=DE、AC=AE
,∠B=∠ADE、∠BAC=∠DAE
3.
BC=DC或AC=EC
,两个三角形全等至少有一组对应边相等
4.C
5.D
6.C
7.D
8.B
9.C
10.D
11.(1)BC=EF或BE=CF
(2)∠CAB=∠FDE
(3)∠ACB=∠DFE[提示:紧扣三角形全等的判定,特别要注意对应相等.]
12.(1)BC=AD
HL (2)∠CAB=∠DBA
AAS
(3)∠CBA=∠DAB AAS (4)AC=BD HL
13.证明:CD⊥AB,BE⊥AC,∴∠ADO=∠BDO=∠AEO=∠CEO=90°.∵AO平分∠BAC,∴∠OAD=∠OAE,又AO=AO,∴△ADO≌△AEO(AAS).∴OD=OE.又DOB=∠EOC,∴△BOD≌△COE(ASA).∴OB=OC.
14.证明△ABE≌△ACE.
15.连接BC,证明△ABC≌△DCB.
16.⑴证明△ADE≌△CBF;⑵证明∠AEF=∠CFE.
17.相等(提示≌)
18.
∴
即
在和中
∴≌(SSS)
19.
∴
在和中
∴≌(ASA)
∴
怎样判定三角形全等
基础过关
1.木工师傅在做完门框后为防止变形,如图所示那样钉上两条斜拉的木板条,这样做的数学依据是_______________________.
1题
2题
2.如图所示,已知△ABC≌△ADE,∠C=∠E,AB=AD,则另外两组对应边为________,另外两组对应角为________.
3.如图所示,AE、BD相交于点C,要使△ABC≌△EDC,至少要添加的条件是________________,理由是________________.
3题
4题
6题
4.如图,相交于E,则图中全等三角形有(
)
A.1对
B.2对
C.3对
D.4对
5.在和中,①,②,③,④,⑤,⑥,则下列各组条件中使和全等的是(
)
A.④⑤⑥
B.①②⑥
C.①③⑤
D.②⑤⑥
6.如图,已知和BF交于点D,①≌;②≌,③D在的平分线上,则以上结论中正确的是(
)
A.只有①
B.只有①②
C.有①②③
D.①和③
能力提升
7.如图,在中,为BC边中点,那么以下结论不正确的是(
)
A.≌
B.
C.AD平分
D.是等边三角形
7题
8题
8.如图,,则(
)
A.45°
B.55°
C.35°
D.65°
9.已知:如图,AB与DC相交于点,若使≌,则(
)
A.应补充条件
B.应补充条件
C.不用补充条件
D.以上说法都不正确
9题
10题
10.如图,已知,则图中全等三角形的总对数是(
)
A.3
B.4
C.5
D.6
11.如图所示,∠ABC=∠DEF,AB=DE,要说明△ABC≌△DEF.
(1)若以“SAS”为依据,还需添加的一个条件是
;
(2)若以“ASA”为依据,还需添加的一个条件是
;
(3)符以“AAS”为依据,还需添加的一个条件是
.
11题
12题
12.如图所示,∠C=∠D=90°,清你添加一个条件,使得△ABC≌△BAD,并在添加的每一个条件后的括号内,写出添加这个条件后判定三角形全等的理由.
(1)
(
):
(2)
(
);
(3)
(
):
(4)
(
).
应用拓展
13.如图所示,CD⊥AB于点D,BE⊥AC于点E,BE,CD交于点O,且AO平分∠BAC.求证OB=OC.
14.如图,AB=AC,BD=CD,求证:∠1=∠2.
15.如图,已知AB=CD,AC=BD,求证:∠A=∠D.
16.如图,AC与BD交于点O,AD=CB,E、F是BD上两点,且AE=CF,DE=BF.请推导下列结论:
⑴∠D=∠B;⑵AE∥CF.
创新突破
17.如图,已知的交点是E,并且与相等吗?试说明你的答案.
18.如图:已知,,那么≌吗?
19.如图,D是的边AB上一点,DF交AC于点,那么吗?
答案
三角形的稳定性
BC=DE、AC=AE
,∠B=∠ADE、∠BAC=∠DAE
3.
BC=DC或AC=EC
,两个三角形全等至少有一组对应边相等
4.C
5.D
6.C
7.D
8.B
9.C
10.D
11.(1)BC=EF或BE=CF
(2)∠CAB=∠FDE
(3)∠ACB=∠DFE[提示:紧扣三角形全等的判定,特别要注意对应相等.]
12.(1)BC=AD
HL (2)∠CAB=∠DBA
AAS
(3)∠CBA=∠DAB AAS (4)AC=BD HL
13.证明:CD⊥AB,BE⊥AC,∴∠ADO=∠BDO=∠AEO=∠CEO=90°.∵AO平分∠BAC,∴∠OAD=∠OAE,又AO=AO,∴△ADO≌△AEO(AAS).∴OD=OE.又DOB=∠EOC,∴△BOD≌△COE(ASA).∴OB=OC.
14.证明△ABE≌△ACE.
15.连接BC,证明△ABC≌△DCB.
16.⑴证明△ADE≌△CBF;⑵证明∠AEF=∠CFE.
17.相等(提示≌)
18.
∴
即
在和中
∴≌(SSS)
19.
∴
在和中
∴≌(ASA)
∴
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
