青岛版八年级数学上册2.5 角平分线的性质-同步练习(word版含答案)
文档属性
| 名称 | 青岛版八年级数学上册2.5 角平分线的性质-同步练习(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 110.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 00:00:00 | ||
图片预览


文档简介
2.5
角平分线的性质
基础过关
1.
如图,OP平分∠AOB,PC⊥OA,PD⊥OB.垂足分别为C,D,则下列结论中错误的是??(??)
A.
PC=PD??B.
OD=OC??C.
∠DPO=∠CPO????D.
PC=OC???
??
1题
2题
2.
如图,若OP平分∠AOB,PM⊥OA于M点,PM=3,N是OB上一个动点,则线段PN的最小值是??(????)
A.
2????B.
3????C.
4???D.
5?????????????
3.下列各语句中,不是真命题的是(
)
A.直角都相等
B.等角的补角相等
C.点P在角的平分线上
D.对顶角相等
4.下列命题中是真命题的是(
)
A.有两角及其中一角的平分线对应相等的两个三角形全等
B.相等的角是对顶角
C.余角相等的角互余
D.两直线被第三条直线所截,截得的同位角相等
5.∠AOB的平分线上一点M
,M到
OA的距离为1.5
cm,则M到OB的距离为_______.
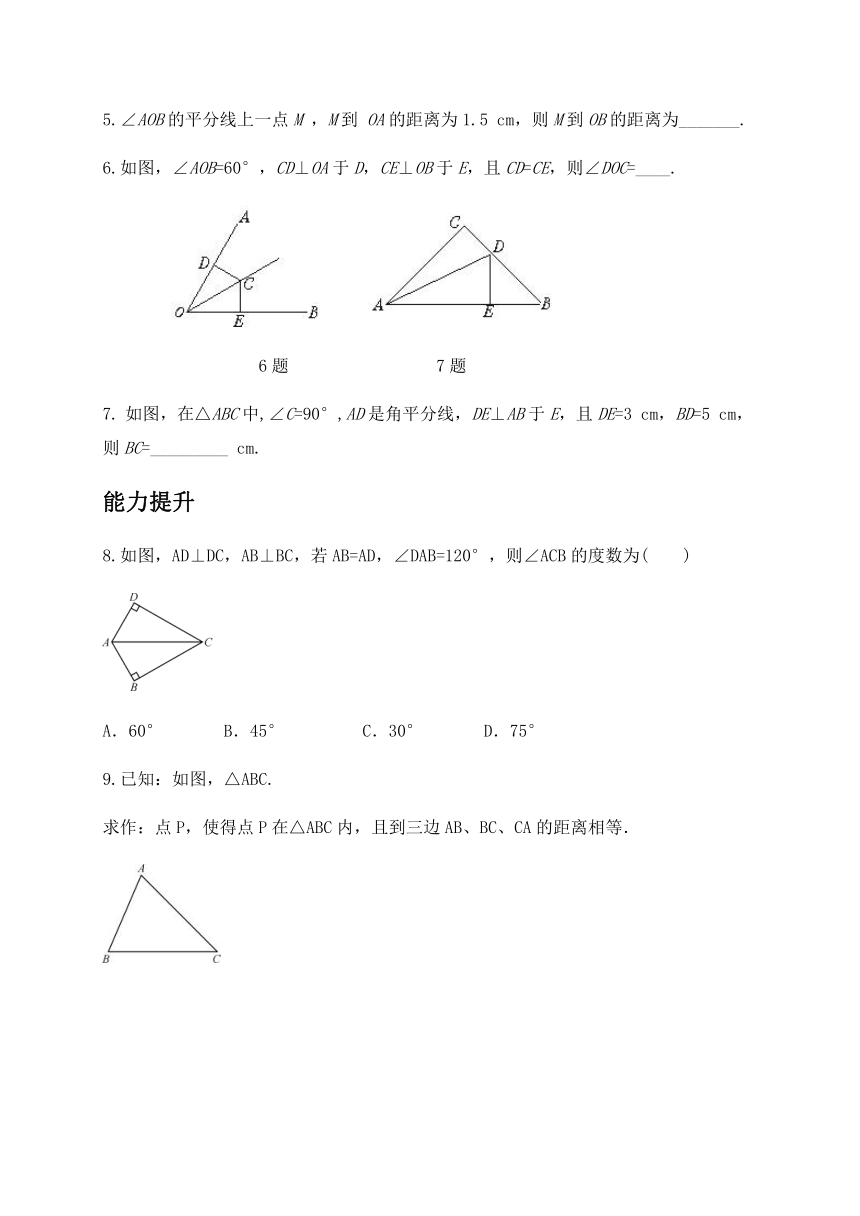
6.如图,∠AOB=60°,CD⊥OA于D,CE⊥OB于E,且CD=CE,则∠DOC=____.
6题
7题
如图,在△ABC中,∠C=90°,AD是角平分线,DE⊥AB于E,且DE=3
cm,BD=5
cm,则BC=_________
cm.
能力提升
8.如图,AD⊥DC,AB⊥BC,若AB=AD,∠DAB=120°,则∠ACB的度数为( )
A.60°
B.45°
C.30°
D.75°
9.已知:如图,△ABC.
求作:点P,使得点P在△ABC内,且到三边AB、BC、CA的距离相等.
10.如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直,若AD=8,则点P到BC的距离是 ( )
?
A.
8?????B.
6???C.
4????D.2?????????????
11.给出下列结论,正确的有(
)
①到角两边距离相等的点,在这个角的平分线上;②角的平分线与三角形平分线都是射线;③任何一个命题都有逆命题;④假命题的逆命题一定是假命题
A.1个
B.2个
C.3个
D.4个
12.下列结论正确的有(
)
①如果(x-1)(x-2)=0,那么x=1;②在△ABC中,若∠B是钝角,则∠A、∠C一定是锐角;③如果两个角相等,那么两个角互为对顶角;④如果在一个角内的点,到这个角的两边距离相等,那么这个点在角的平分线上
A.1个
B.2个
C.3个
D.4个
13.已知,Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D,若BC=32,且BD∶CD=9∶7,则D到AB的距离为(
)
A.18
B.16
C.14
D.12
应用拓展
14.如图,在△ABC中,P,Q分别是BC,AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R,S,若AQ=PQ,PR=PS,则下面三个结论:①AS=AR,②QP∥AR,③△BRP≌△CSP,其中正确的是??(????)
A.
①③???B.
②③??C.
①②????D.
①②③?
???
14题
15题
15.
如图所示,点,分别是,平分线上的点,于点,于点,于点,下列结论错误的是(????)
A.
B.
与互余的角有两个
C.
?D.
点是的中点?????????????
16.如图,在△ACB中,∠ACB=100°,∠A=20°,D是AB上一点.将△ABC沿CD折叠,使B点落在AC边上的B′处,则∠ADB′等于(
)
A.25°
B.30°
C.35°
D.40°
16题
17题
18题
17.如图,OP是∠AOB的平分线,点P到OA的距离为3,点N是OB上的任意一点,则线段PN的取值范围为(
)
A.PN<3
B.PN>3
C.PN≥3
D.PN≤3
18.如图,三条公路把A、B、C三个村庄连成一个三角形区域,某地区决定在这个三角形区域内修建一个集贸市场,要使集贸市场到三个条公路的距离相等,则这个集贸市场应建在( )
A.在AC、BC两边高线的交点处
B.在AC、BC两边中线的交点处
C.在∠A、∠B两内角平分线的交点处
D.在AC、BC两边垂直平分线的交点处
创新突破
19.如图,已知BE⊥AC于E,CF⊥AB于F,BE、CF相交于点D,若BD=CD.求证:AD平分∠BAC
20如图,在△ABC中,CA=CB,,AD平分,于点E,AB=10?cm.求△BED的周长.
?
答案
D
2.
B
3.
C
4.
A
5.
1.5cm
6.
30°
7.
8
8.
C
9.作图略
作法:(提示)作三个内角平分线交于一点P,点P即为所求作的点.
10.
C
11.
B
12.
B
13.
C
14.
C
15.
B
16.
D
17.
C
18.
C
19.证明:在△BDF和△CDE中
∴△BDF≌△CDE,∴DF=DE
∴D在∠A的平分线上,∴AD平分∠BAC.
解:∵,,∴CD=DE.
又∵AD=AD,∴,∴,AC=AE,∴BD+DE=BD+DC=BC.
?∵AC=CB,∴BD+DE=BC=CA=AE,∴BD+DE+BE=AE+BE=AB=10?cm,∴△BED的周长为10?cm.
角平分线的性质
基础过关
1.
如图,OP平分∠AOB,PC⊥OA,PD⊥OB.垂足分别为C,D,则下列结论中错误的是??(??)
A.
PC=PD??B.
OD=OC??C.
∠DPO=∠CPO????D.
PC=OC???
??
1题
2题
2.
如图,若OP平分∠AOB,PM⊥OA于M点,PM=3,N是OB上一个动点,则线段PN的最小值是??(????)
A.
2????B.
3????C.
4???D.
5?????????????
3.下列各语句中,不是真命题的是(
)
A.直角都相等
B.等角的补角相等
C.点P在角的平分线上
D.对顶角相等
4.下列命题中是真命题的是(
)
A.有两角及其中一角的平分线对应相等的两个三角形全等
B.相等的角是对顶角
C.余角相等的角互余
D.两直线被第三条直线所截,截得的同位角相等
5.∠AOB的平分线上一点M
,M到
OA的距离为1.5
cm,则M到OB的距离为_______.
6.如图,∠AOB=60°,CD⊥OA于D,CE⊥OB于E,且CD=CE,则∠DOC=____.
6题
7题
如图,在△ABC中,∠C=90°,AD是角平分线,DE⊥AB于E,且DE=3
cm,BD=5
cm,则BC=_________
cm.
能力提升
8.如图,AD⊥DC,AB⊥BC,若AB=AD,∠DAB=120°,则∠ACB的度数为( )
A.60°
B.45°
C.30°
D.75°
9.已知:如图,△ABC.
求作:点P,使得点P在△ABC内,且到三边AB、BC、CA的距离相等.
10.如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直,若AD=8,则点P到BC的距离是 ( )
?
A.
8?????B.
6???C.
4????D.2?????????????
11.给出下列结论,正确的有(
)
①到角两边距离相等的点,在这个角的平分线上;②角的平分线与三角形平分线都是射线;③任何一个命题都有逆命题;④假命题的逆命题一定是假命题
A.1个
B.2个
C.3个
D.4个
12.下列结论正确的有(
)
①如果(x-1)(x-2)=0,那么x=1;②在△ABC中,若∠B是钝角,则∠A、∠C一定是锐角;③如果两个角相等,那么两个角互为对顶角;④如果在一个角内的点,到这个角的两边距离相等,那么这个点在角的平分线上
A.1个
B.2个
C.3个
D.4个
13.已知,Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D,若BC=32,且BD∶CD=9∶7,则D到AB的距离为(
)
A.18
B.16
C.14
D.12
应用拓展
14.如图,在△ABC中,P,Q分别是BC,AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R,S,若AQ=PQ,PR=PS,则下面三个结论:①AS=AR,②QP∥AR,③△BRP≌△CSP,其中正确的是??(????)
A.
①③???B.
②③??C.
①②????D.
①②③?
???
14题
15题
15.
如图所示,点,分别是,平分线上的点,于点,于点,于点,下列结论错误的是(????)
A.
B.
与互余的角有两个
C.
?D.
点是的中点?????????????
16.如图,在△ACB中,∠ACB=100°,∠A=20°,D是AB上一点.将△ABC沿CD折叠,使B点落在AC边上的B′处,则∠ADB′等于(
)
A.25°
B.30°
C.35°
D.40°
16题
17题
18题
17.如图,OP是∠AOB的平分线,点P到OA的距离为3,点N是OB上的任意一点,则线段PN的取值范围为(
)
A.PN<3
B.PN>3
C.PN≥3
D.PN≤3
18.如图,三条公路把A、B、C三个村庄连成一个三角形区域,某地区决定在这个三角形区域内修建一个集贸市场,要使集贸市场到三个条公路的距离相等,则这个集贸市场应建在( )
A.在AC、BC两边高线的交点处
B.在AC、BC两边中线的交点处
C.在∠A、∠B两内角平分线的交点处
D.在AC、BC两边垂直平分线的交点处
创新突破
19.如图,已知BE⊥AC于E,CF⊥AB于F,BE、CF相交于点D,若BD=CD.求证:AD平分∠BAC
20如图,在△ABC中,CA=CB,,AD平分,于点E,AB=10?cm.求△BED的周长.
?
答案
D
2.
B
3.
C
4.
A
5.
1.5cm
6.
30°
7.
8
8.
C
9.作图略
作法:(提示)作三个内角平分线交于一点P,点P即为所求作的点.
10.
C
11.
B
12.
B
13.
C
14.
C
15.
B
16.
D
17.
C
18.
C
19.证明:在△BDF和△CDE中
∴△BDF≌△CDE,∴DF=DE
∴D在∠A的平分线上,∴AD平分∠BAC.
解:∵,,∴CD=DE.
又∵AD=AD,∴,∴,AC=AE,∴BD+DE=BD+DC=BC.
?∵AC=CB,∴BD+DE=BC=CA=AE,∴BD+DE+BE=AE+BE=AB=10?cm,∴△BED的周长为10?cm.
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
