人教版数学八年级上册导学案:11.1与三角形有关的线段(无答案)
文档属性
| 名称 | 人教版数学八年级上册导学案:11.1与三角形有关的线段(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 513.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 00:00:00 | ||
图片预览



文档简介
与三角形有关的线段
一、目标与策略
明确学习目标及主要的学习方法是提高学习效率的首要条件,要做到心中有数!
学习目标:
认识三角形,以及三角形的边、内角、顶点,能用符号语言表示三角形,
理解并会应用三角形三边间的关系.
理解三角形的高、中线、角平分线的概念,通过作三角形的三条高、中线、角平分线,提高基本作图能力,并能运用图形解决问题.
通过作图、观察、比较、描述图形等数学活动,感受数学的严谨性,图形中蕴含的规律性,提高学习数学的热情及大担探究新知识的创新能力.
通过观察和实地操作知道三角形具有稳定性,知道四边形没有稳定性,了解稳定性与没有稳定性在生产、生活中的广泛应用.
重点:
三角形三边间的关系;
三角形的高、中线、角平分线的概念,并能在具体的三角形中画出它们;
三角形稳定性在生产、生活中的实际应用.
难点:
用三角形三边关系判定三条线段可否组成三角形.
在各种三角形中作出它们的高.
学习策略:
通过观察、画图等实践过程认识三角形的三边间的关系及高、中线与角平分线,经历实地操作得到三角形具有稳定性,四边形没有稳定性.
二、学习与应用
(一)三角形的面积=
(二)两个完全一样的三角形能拼
(三)一个三角形底是5cm,高是7cm,面积是 .
(四)一个三角形的面积是4.8m2,与它等底等高的平行四边形的面积是 .
(五)有一个三角形花坛,想把它平均分成两个相等的三角形,可以怎样分?
(六)直角三角形底3,
高4,
斜边5,
求面积
知识点一:三角形
(一)三角形有关概念
(1)三角形的定义:由不在同一条 上的三条线段 顺次相接组成的图形叫做三角形.
(2)三角形的基本元素:
①三角形的三条边:即组成三角形的 ;
②三角形的角:即相邻两边所组成的角叫做三角形的 ;三角形的一边与另一边的延长线所组成的角叫做三角形的 .
③三角形的顶点:即相邻两边的公共 .
(3)三角形的特征:
①三条线段不在同一直线上,且 顺次相接;
②三角形是一个 的图形.
(4)三角形的符号:
①三角形用符号“ ”表示.顶点是A、B、C的三角形,记作“ ”,读作“三角形ABC”;注意:△ABC是三角形ABC的符号标记,单独的△没有意义
②三角形ABC的边AB可用边AB所对的角C的小写字母c表示,AC可用b表示,BC可用a表示.
(二)三角形的分类
(1)按边分类:
要点诠释:
①不等边三角形:三边都不__________的三角形
②等腰三角形:有两条边 的三角形叫做等腰三角形,相等的两边都叫做 ,另外一边叫做 ,两腰的夹角叫 ,腰与底边夹角叫做 .
③等边三角形:三边都__________的三角形
(2)按角分类:
要点诠释:
①锐角三角形:三个内角都是 的三角形
②钝角三角形:有一个内角为 的三角形
知识点二:三角形三边间的关系
定理:三角形任意两边之和
第三边.
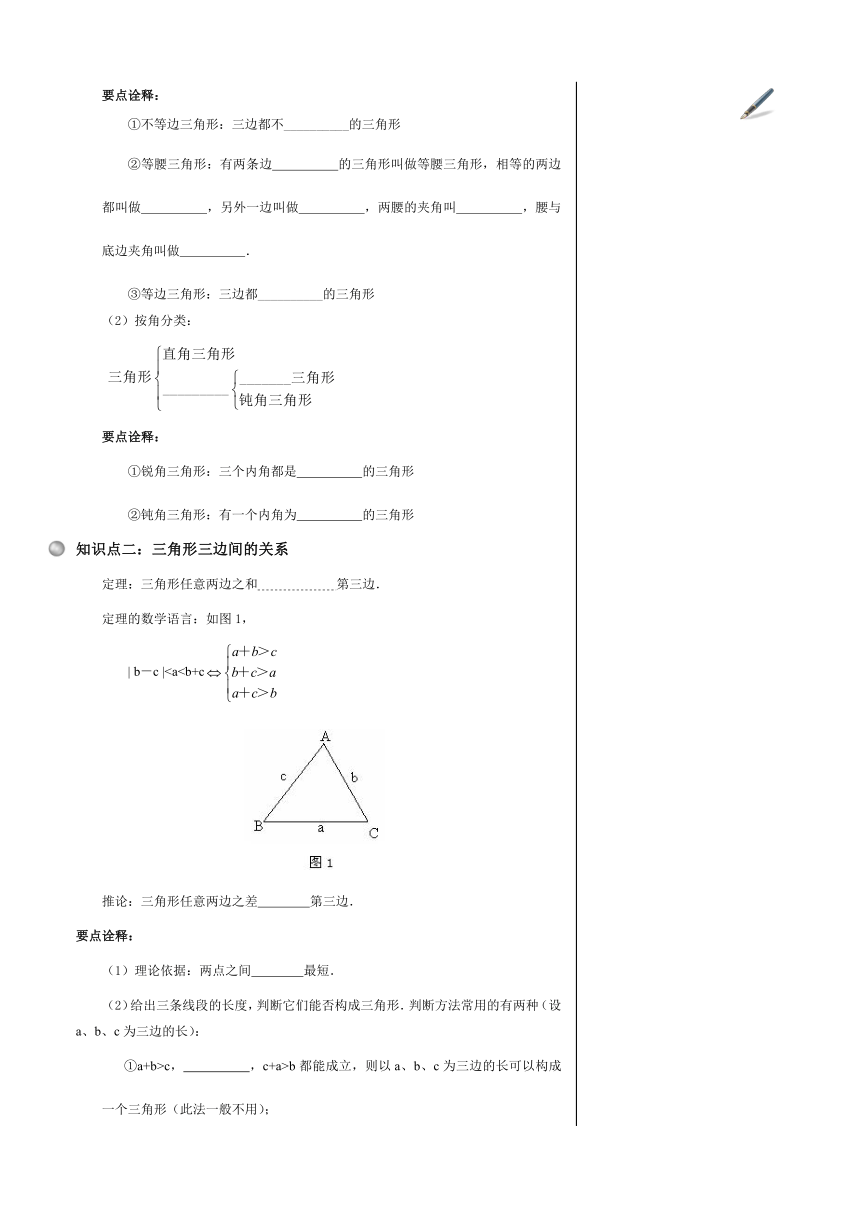
定理的数学语言:如图1,
|
b-c
|推论:三角形任意两边之差 第三边.
要点诠释:
(1)理论依据:两点之间 最短.
(2)给出三条线段的长度,判断它们能否构成三角形.判断方法常用的有两种(设a、b、c为三边的长):
①a+b>c,
,c+a>b都能成立,则以a、b、c为三边的长可以构成一个三角形(此法一般不用);
②|b-c| 长为a,b,c的三条线段可组成三角形;或若c是最长的线段,且 ,则以a、b、c为三边的长可构成一个三角形.
(3)已知三角形两边的长,可以确定第三边的取值范围:设三角形的两边的长为a、b,则第三边的长c的取值范围是 .
(4)证明线段之间的不等关系.
知识点三:三角形的高、中线、角平分线
(一)三角形的高
从三角形的一个顶点向它的
所在直线作垂线, 和 之间的线段叫做三角形的高线,简称三角形的高.
三角形的高的数学语言:
如图2,AD是△ABC的高,或AD是△ABC的BC边上的高,或AD⊥BC于D,或∠ADB=∠ADC=∠90°.
注意:AD是△ABC的高∠ADB=∠ADC= °(或AD⊥BC于D);
要点诠释:
(1)三角形的高是 ;
(2)三角形有三条高,且相交于一点,这一点叫做三角形的_______.
(3)三角形的三条高:
①锐角三角形的三条高在三角形
部,三条高的交点也在三角形
部;
②钝角三角形有两条高在三角形的
部,且三条高的交点在三角形的
部;
③直角三角形三条高的交点是直角三角形的 .
(二)三角形的中线
三角形的一个顶点与它的对边 的连线叫三角形的中线.
三角形的中线的数学语言:
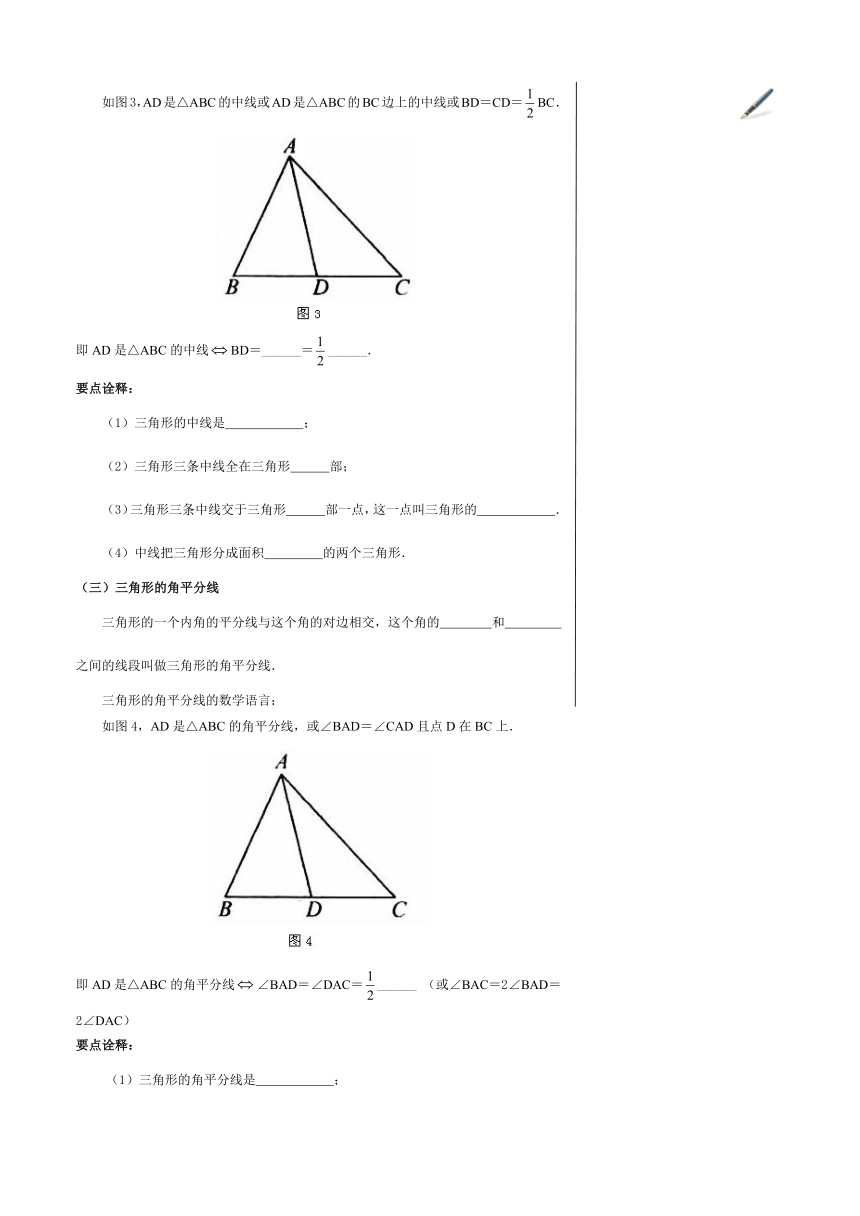
如图3,AD是△ABC的中线或AD是△ABC的BC边上的中线或BD=CD=BC.
即AD是△ABC的中线BD=______=______.
要点诠释:
(1)三角形的中线是 ;
(2)三角形三条中线全在三角形 部;
(3)三角形三条中线交于三角形 部一点,这一点叫三角形的 .
(4)中线把三角形分成面积
的两个三角形.
(三)三角形的角平分线
三角形的一个内角的平分线与这个角的对边相交,这个角的
和
之间的线段叫做三角形的角平分线.
三角形的角平分线的数学语言:
如图4,AD是△ABC的角平分线,或∠BAD=∠CAD且点D在BC上.
即AD是△ABC的角平分线∠BAD=∠DAC=______
(或∠BAC=2∠BAD=2∠DAC)
要点诠释:
(1)三角形的角平分线是 ;
(2)一个三角形有三条角平分线,并且都在三角形的 部;
(3)三角形三条角平分线交于三角形
部一点,这一点叫做三角形的
.
(4)可以用
或
画三角形的角平分线.
知识点四:三角形的稳定性
如果三角形的三边固定,那么三角形的形状大小就完全固定了,这个性质叫做三角形的 .
要点诠释:
(1)三角形的形状固定是指三角形的三个
角不会改变,大小固定指三条
不改变.
(2)三角形的稳定性在生产和生活中很有用.例如,房屋的人字梁具有三角形的结构,它就坚固而稳定;在栅栏门上斜着钉一条(或两条)木板,构成一个三角形,就可以使栅栏门不变形.大桥钢架、输电线支架都采用三角形结构,也是这个道理.
(3)四边形没有稳定性,也就是说,四边形的四条边长确定后,不能确定它的形状,它的各个角的大小可以改变.四边形的不稳定性也有广泛应用,如活动挂架,伸缩尺.有时我们又要克服四边形的不稳定性,如在窗框未安好之前,先在窗框上斜着钉一根木板,使它不变形.
类型一:三角形的概念
例1.图5中以BC为边的三角形有几个?用符号表示这些三角形.
思路点拨:三角形有 个顶点,在给定一条边BC后,只须再找一个顶点就可以了.
解析:
总结升华:
举一反三:
【变式1】在图5中,以A为顶点的三角形有几个?用符号表示这些三角形.
答案:
【变式2】在图5中,具有公共边AB的三角形有几个?用符号表示这些三角形.
答案:
类型二:三角形三边关系
例2.下列长度的各组线段中,能组成三角形的是(
)
A.3cm,12cm,8cm
B.6cm,8cm,15cm
C.2.5cm,3cm,5cm
D.6.3cm,6.3cm,12.6cm
思路点拨:本例可用三角形三边之间的关系判定三角形,结合排除法使问题得以解决.
解析:
总结升华:
举一反三:
【变式1】已知三条线段的比是:①1:3:4;②1:2:3;③1:4:6;④3:3:6;⑤6:6:10;⑥3:4:5.其中可构成三角形的有(
)
A.1个
B.2个
C.3个
D.4个
答案:
【变式2】若五条线段的长分别是1cm、2cm、3cm、4cm、5cm,则以其中三条线段为边可构成 个三角形.
答案:
【变式3】已知三角形的两边长分别4cm和9cm,则下列长度的四条线段中能作为第三边的是(
)
A.13cm
B.6cm
C.5cm
D.4cm
思路点拨:
选取的第三边一定小于 而大于 的绝对值.
解析:
答案:
【变式4】已知a、b、c是△ABC的三边,化简|a+b-c|+|b-a-c|-|c+b-a|.
思路点拨:运用三角形三边的关系确定绝对值内式子的符号,然后根据绝对值的法则去绝对值.
答案:
☆【变式5】用7根火柴棒首尾顺次连结摆成一个三角形,能摆成不同的三角形的个数 .
思路点拨:
解题的关键是确定出最大边的范围.
解析:
答案:
例3.若三角形的两边长分别是2和7,则第三边长c的取值范围是 .
思路点拨:三角形的两边a、b,那么第三边c的取值范围是 .
解析:
三角形的两边长分别是2和7,
则第三边长c的取值范围是
,即 .
总结升华:
举一反三:
【变式1】如果三角形的两边长分别为2和6,则周长L的取值范围是(
)
A.6B.6C.11D.12答案:
【变式2】已知等腰三角形的两边长分别为4cm和7cm,且它的周长大于16cm,则第三边长为 .
答案:
☆例4.已知等腰三角形一腰上的中线将这个三角形的周长分为9cm和15cm两部分,求这个三角形的腰长和底边的长.
思路点拨:本题分 种情况讨论,但讨论的结果不一定有两个正确答案,要加以合理取舍.
解析:
总结升华:
举一反三:
【变式】小芳要画一个有两边长分别为5cm和6cm的等腰三角形,则这个等腰三角形的周长是(
)
A.16cm B.17cm C.16cm或17cm D.11cm
答案:
类型三:三角形的高、中线、角平分线
例5.如图6,在锐角△ABC中,CD、BE分别是AB、AC上的高,且CD、BE交于一点P,若∠A=50°,则∠BPC的度数是(
)
A.150°
B.130°
C.120°
D.100°
思路点拨:本题主要考查对三角形的高的性质、互余和互补角的性质以及小学学过的常识性的问题------三角形的内角和是 .
解析:
答案:
总结升华:
举一反三:
【变式1】如图7所示,在△ABC中,∠C-∠B=90°,AE是∠BAC的平分线,求∠AEC的度数.
答案:
【变式2】在△ABC中,∠B=60°,∠C=40°,AD、AE分别是△ABC的高线和角平分线,
则∠DAE的度数为
.
答案:
【变式3】如图8所示,已知AD,AE分别是△ABC的中线、高,且AB=5cm,AC=3cm,则△ABD与△ACD的周长之差为 ,△ABD与△ACD的面积关系为
.
解析:
答案:
三、总结与测评
要想学习成绩好,总结测评少不了!课后复习是学习不可或缺的环节,它可以帮助我们巩固学习效果,弥补知识缺漏,提高学习能力.
(一)把所学的三角形有关的线段知识与前面已学过的相关知识相结合,形成系统的知识网络.
(二)应用三边关系判断三条线段是否构成三角形,只要两条 的线段长度之和大于第三条线段的长度,即可判定这三
条线段能构成一个三角形.
(三)已知三角形的两边a、b,那么第三边c的取值范围是 .
(四)数形结合是学习数学有效的方法之一,在学习这部分知识的过程中,需要多画图,在图形中理解知识的含义,弄清各部分之间的关系.
我的收获
习题整理
题目或题目出处
所属类型或知识点
分析及注意问题
好题
错题
注:本表格为建议样式,请同学们单独建立错题本
一、目标与策略
明确学习目标及主要的学习方法是提高学习效率的首要条件,要做到心中有数!
学习目标:
认识三角形,以及三角形的边、内角、顶点,能用符号语言表示三角形,
理解并会应用三角形三边间的关系.
理解三角形的高、中线、角平分线的概念,通过作三角形的三条高、中线、角平分线,提高基本作图能力,并能运用图形解决问题.
通过作图、观察、比较、描述图形等数学活动,感受数学的严谨性,图形中蕴含的规律性,提高学习数学的热情及大担探究新知识的创新能力.
通过观察和实地操作知道三角形具有稳定性,知道四边形没有稳定性,了解稳定性与没有稳定性在生产、生活中的广泛应用.
重点:
三角形三边间的关系;
三角形的高、中线、角平分线的概念,并能在具体的三角形中画出它们;
三角形稳定性在生产、生活中的实际应用.
难点:
用三角形三边关系判定三条线段可否组成三角形.
在各种三角形中作出它们的高.
学习策略:
通过观察、画图等实践过程认识三角形的三边间的关系及高、中线与角平分线,经历实地操作得到三角形具有稳定性,四边形没有稳定性.
二、学习与应用
(一)三角形的面积=
(二)两个完全一样的三角形能拼
(三)一个三角形底是5cm,高是7cm,面积是 .
(四)一个三角形的面积是4.8m2,与它等底等高的平行四边形的面积是 .
(五)有一个三角形花坛,想把它平均分成两个相等的三角形,可以怎样分?
(六)直角三角形底3,
高4,
斜边5,
求面积
知识点一:三角形
(一)三角形有关概念
(1)三角形的定义:由不在同一条 上的三条线段 顺次相接组成的图形叫做三角形.
(2)三角形的基本元素:
①三角形的三条边:即组成三角形的 ;
②三角形的角:即相邻两边所组成的角叫做三角形的 ;三角形的一边与另一边的延长线所组成的角叫做三角形的 .
③三角形的顶点:即相邻两边的公共 .
(3)三角形的特征:
①三条线段不在同一直线上,且 顺次相接;
②三角形是一个 的图形.
(4)三角形的符号:
①三角形用符号“ ”表示.顶点是A、B、C的三角形,记作“ ”,读作“三角形ABC”;注意:△ABC是三角形ABC的符号标记,单独的△没有意义
②三角形ABC的边AB可用边AB所对的角C的小写字母c表示,AC可用b表示,BC可用a表示.
(二)三角形的分类
(1)按边分类:
要点诠释:
①不等边三角形:三边都不__________的三角形
②等腰三角形:有两条边 的三角形叫做等腰三角形,相等的两边都叫做 ,另外一边叫做 ,两腰的夹角叫 ,腰与底边夹角叫做 .
③等边三角形:三边都__________的三角形
(2)按角分类:
要点诠释:
①锐角三角形:三个内角都是 的三角形
②钝角三角形:有一个内角为 的三角形
知识点二:三角形三边间的关系
定理:三角形任意两边之和
第三边.
定理的数学语言:如图1,
|
b-c
|
要点诠释:
(1)理论依据:两点之间 最短.
(2)给出三条线段的长度,判断它们能否构成三角形.判断方法常用的有两种(设a、b、c为三边的长):
①a+b>c,
,c+a>b都能成立,则以a、b、c为三边的长可以构成一个三角形(此法一般不用);
②|b-c|
(3)已知三角形两边的长,可以确定第三边的取值范围:设三角形的两边的长为a、b,则第三边的长c的取值范围是 .
(4)证明线段之间的不等关系.
知识点三:三角形的高、中线、角平分线
(一)三角形的高
从三角形的一个顶点向它的
所在直线作垂线, 和 之间的线段叫做三角形的高线,简称三角形的高.
三角形的高的数学语言:
如图2,AD是△ABC的高,或AD是△ABC的BC边上的高,或AD⊥BC于D,或∠ADB=∠ADC=∠90°.
注意:AD是△ABC的高∠ADB=∠ADC= °(或AD⊥BC于D);
要点诠释:
(1)三角形的高是 ;
(2)三角形有三条高,且相交于一点,这一点叫做三角形的_______.
(3)三角形的三条高:
①锐角三角形的三条高在三角形
部,三条高的交点也在三角形
部;
②钝角三角形有两条高在三角形的
部,且三条高的交点在三角形的
部;
③直角三角形三条高的交点是直角三角形的 .
(二)三角形的中线
三角形的一个顶点与它的对边 的连线叫三角形的中线.
三角形的中线的数学语言:
如图3,AD是△ABC的中线或AD是△ABC的BC边上的中线或BD=CD=BC.
即AD是△ABC的中线BD=______=______.
要点诠释:
(1)三角形的中线是 ;
(2)三角形三条中线全在三角形 部;
(3)三角形三条中线交于三角形 部一点,这一点叫三角形的 .
(4)中线把三角形分成面积
的两个三角形.
(三)三角形的角平分线
三角形的一个内角的平分线与这个角的对边相交,这个角的
和
之间的线段叫做三角形的角平分线.
三角形的角平分线的数学语言:
如图4,AD是△ABC的角平分线,或∠BAD=∠CAD且点D在BC上.
即AD是△ABC的角平分线∠BAD=∠DAC=______
(或∠BAC=2∠BAD=2∠DAC)
要点诠释:
(1)三角形的角平分线是 ;
(2)一个三角形有三条角平分线,并且都在三角形的 部;
(3)三角形三条角平分线交于三角形
部一点,这一点叫做三角形的
.
(4)可以用
或
画三角形的角平分线.
知识点四:三角形的稳定性
如果三角形的三边固定,那么三角形的形状大小就完全固定了,这个性质叫做三角形的 .
要点诠释:
(1)三角形的形状固定是指三角形的三个
角不会改变,大小固定指三条
不改变.
(2)三角形的稳定性在生产和生活中很有用.例如,房屋的人字梁具有三角形的结构,它就坚固而稳定;在栅栏门上斜着钉一条(或两条)木板,构成一个三角形,就可以使栅栏门不变形.大桥钢架、输电线支架都采用三角形结构,也是这个道理.
(3)四边形没有稳定性,也就是说,四边形的四条边长确定后,不能确定它的形状,它的各个角的大小可以改变.四边形的不稳定性也有广泛应用,如活动挂架,伸缩尺.有时我们又要克服四边形的不稳定性,如在窗框未安好之前,先在窗框上斜着钉一根木板,使它不变形.
类型一:三角形的概念
例1.图5中以BC为边的三角形有几个?用符号表示这些三角形.
思路点拨:三角形有 个顶点,在给定一条边BC后,只须再找一个顶点就可以了.
解析:
总结升华:
举一反三:
【变式1】在图5中,以A为顶点的三角形有几个?用符号表示这些三角形.
答案:
【变式2】在图5中,具有公共边AB的三角形有几个?用符号表示这些三角形.
答案:
类型二:三角形三边关系
例2.下列长度的各组线段中,能组成三角形的是(
)
A.3cm,12cm,8cm
B.6cm,8cm,15cm
C.2.5cm,3cm,5cm
D.6.3cm,6.3cm,12.6cm
思路点拨:本例可用三角形三边之间的关系判定三角形,结合排除法使问题得以解决.
解析:
总结升华:
举一反三:
【变式1】已知三条线段的比是:①1:3:4;②1:2:3;③1:4:6;④3:3:6;⑤6:6:10;⑥3:4:5.其中可构成三角形的有(
)
A.1个
B.2个
C.3个
D.4个
答案:
【变式2】若五条线段的长分别是1cm、2cm、3cm、4cm、5cm,则以其中三条线段为边可构成 个三角形.
答案:
【变式3】已知三角形的两边长分别4cm和9cm,则下列长度的四条线段中能作为第三边的是(
)
A.13cm
B.6cm
C.5cm
D.4cm
思路点拨:
选取的第三边一定小于 而大于 的绝对值.
解析:
答案:
【变式4】已知a、b、c是△ABC的三边,化简|a+b-c|+|b-a-c|-|c+b-a|.
思路点拨:运用三角形三边的关系确定绝对值内式子的符号,然后根据绝对值的法则去绝对值.
答案:
☆【变式5】用7根火柴棒首尾顺次连结摆成一个三角形,能摆成不同的三角形的个数 .
思路点拨:
解题的关键是确定出最大边的范围.
解析:
答案:
例3.若三角形的两边长分别是2和7,则第三边长c的取值范围是 .
思路点拨:三角形的两边a、b,那么第三边c的取值范围是 .
解析:
三角形的两边长分别是2和7,
则第三边长c的取值范围是
,即 .
总结升华:
举一反三:
【变式1】如果三角形的两边长分别为2和6,则周长L的取值范围是(
)
A.6
【变式2】已知等腰三角形的两边长分别为4cm和7cm,且它的周长大于16cm,则第三边长为 .
答案:
☆例4.已知等腰三角形一腰上的中线将这个三角形的周长分为9cm和15cm两部分,求这个三角形的腰长和底边的长.
思路点拨:本题分 种情况讨论,但讨论的结果不一定有两个正确答案,要加以合理取舍.
解析:
总结升华:
举一反三:
【变式】小芳要画一个有两边长分别为5cm和6cm的等腰三角形,则这个等腰三角形的周长是(
)
A.16cm B.17cm C.16cm或17cm D.11cm
答案:
类型三:三角形的高、中线、角平分线
例5.如图6,在锐角△ABC中,CD、BE分别是AB、AC上的高,且CD、BE交于一点P,若∠A=50°,则∠BPC的度数是(
)
A.150°
B.130°
C.120°
D.100°
思路点拨:本题主要考查对三角形的高的性质、互余和互补角的性质以及小学学过的常识性的问题------三角形的内角和是 .
解析:
答案:
总结升华:
举一反三:
【变式1】如图7所示,在△ABC中,∠C-∠B=90°,AE是∠BAC的平分线,求∠AEC的度数.
答案:
【变式2】在△ABC中,∠B=60°,∠C=40°,AD、AE分别是△ABC的高线和角平分线,
则∠DAE的度数为
.
答案:
【变式3】如图8所示,已知AD,AE分别是△ABC的中线、高,且AB=5cm,AC=3cm,则△ABD与△ACD的周长之差为 ,△ABD与△ACD的面积关系为
.
解析:
答案:
三、总结与测评
要想学习成绩好,总结测评少不了!课后复习是学习不可或缺的环节,它可以帮助我们巩固学习效果,弥补知识缺漏,提高学习能力.
(一)把所学的三角形有关的线段知识与前面已学过的相关知识相结合,形成系统的知识网络.
(二)应用三边关系判断三条线段是否构成三角形,只要两条 的线段长度之和大于第三条线段的长度,即可判定这三
条线段能构成一个三角形.
(三)已知三角形的两边a、b,那么第三边c的取值范围是 .
(四)数形结合是学习数学有效的方法之一,在学习这部分知识的过程中,需要多画图,在图形中理解知识的含义,弄清各部分之间的关系.
我的收获
习题整理
题目或题目出处
所属类型或知识点
分析及注意问题
好题
错题
注:本表格为建议样式,请同学们单独建立错题本
