人教版数学九年级下册 第28章 28.2解直角三角形及其应用同步测试试题(word版含答案)
文档属性
| 名称 | 人教版数学九年级下册 第28章 28.2解直角三角形及其应用同步测试试题(word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 281.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 18:37:05 | ||
图片预览


文档简介
解直角三角形及其应用同步测试试题(一)
一.选择题
1.已知,一轮船以16海里/时的速度从港口A出发向北偏东63°方向航行,另一轮船以8海里/时的速度同时从港口A出发向南偏东57°方向航行.离开港口1小时后,则两船相距( )
A.8海里
B.8海里
C.16海里
D.24海里
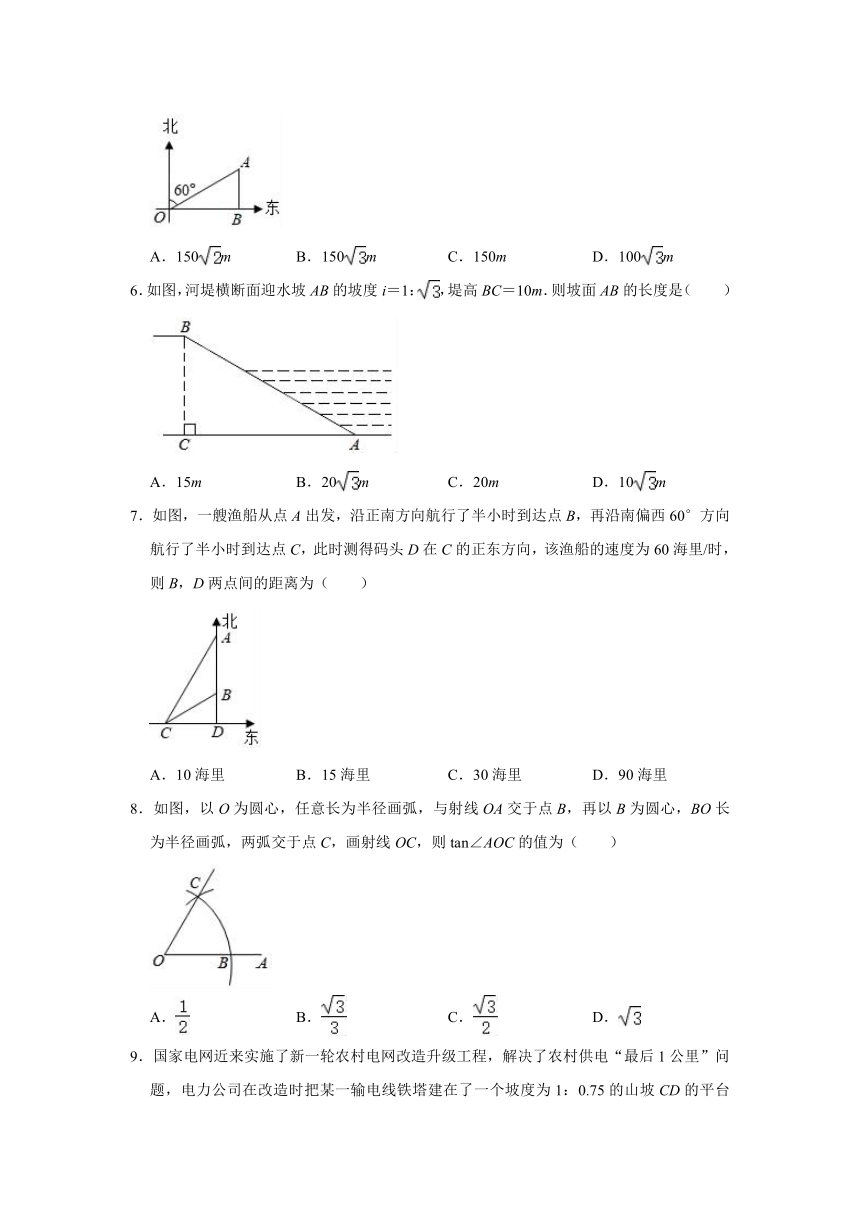
2.如图,在Rt△ABC中,∠ABC=90°,BD⊥AC于点D,AB=2BC,则tan∠ABD的值为( )
A.2
B.
C.
D.
3.如图,小正方形的边长均为1,A、B、C分别是小正方形的三个顶点,则sin∠BAC的值为( )
A.
B.
C.1
D.
4.如图,河坝横断面迎水坡AB的坡比为1:,坝高BC=4m,则AB的长度为( )
A.2m
B.4m
C.4m
D.6m
5.如图,小明在一条东西走向公路的O处,测得图书馆A在他的北偏东60°方向,且与他相距300m,则图书馆A到公路的距离AB为( )
A.150m
B.150m
C.150m
D.100m
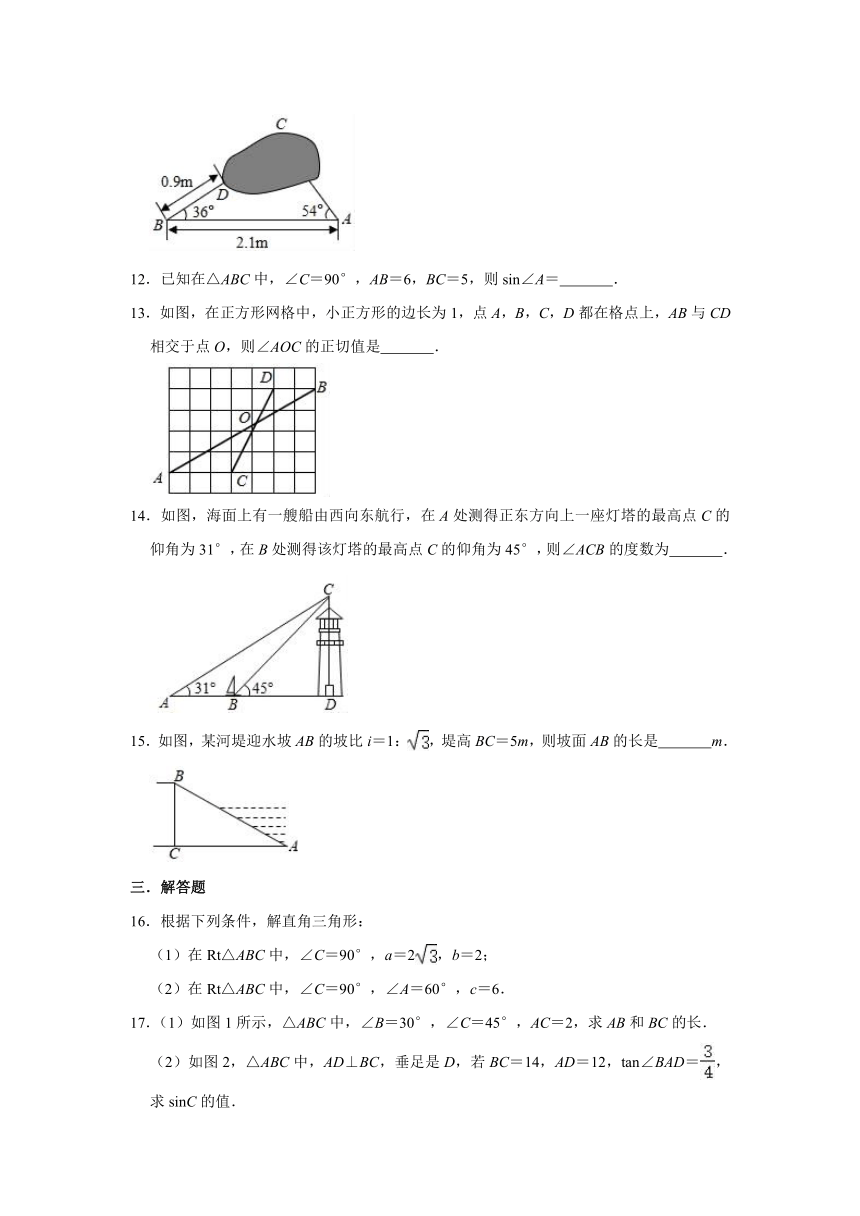
6.如图,河堤横断面迎水坡AB的坡度i=1:,堤高BC=10m.则坡面AB的长度是( )
A.15m
B.20m
C.20m
D.10m
7.如图,一艘渔船从点A出发,沿正南方向航行了半小时到达点B,再沿南偏西60°方向航行了半小时到达点C,此时测得码头D在C的正东方向,该渔船的速度为60海里/时,则B,D两点间的距离为( )
A.10海里
B.15海里
C.30海里
D.90海里
8.如图,以O为圆心,任意长为半径画弧,与射线OA交于点B,再以B为圆心,BO长为半径画弧,两弧交于点C,画射线OC,则tan∠AOC的值为( )
A.
B.
C.
D.
9.国家电网近来实施了新一轮农村电网改造升级工程,解决了农村供电“最后1公里”问题,电力公司在改造时把某一输电线铁塔建在了一个坡度为1:0.75的山坡CD的平台BC上(如图),测得∠AED=52.5°,BC=5米,CD=35米,DE=19米,则铁塔AB的高度约为(参考数据:sin52.5°≈0.79,cos52.5°≈0.61,tan52.5°≈1.30)( )
A.7.6米
B.27.5米
C.30.5米
D.58.5米
10.如图,校园内有两栋教学楼求真楼AB和行知楼CD,已知CD的高度为21米,为测量AB的高度,小诚先在行知楼顶端D处测得求真楼顶端A处的仰角为14°,然后下楼从行知楼底部点C出发,先沿坡度为1:2.4的斜坡行走2.6米到达点E,再沿水平方向前进47.6米到达求真楼底端点B(A,B,C,D,E在同一平面内),则求真楼AB的高度约为( )
(参考数据:sin14°≈0.24,cos14°≈0.97,tan14°≈0.25)
A.31.5米
B.32.5米
C.33.5米
D.34.5米
二.填空题
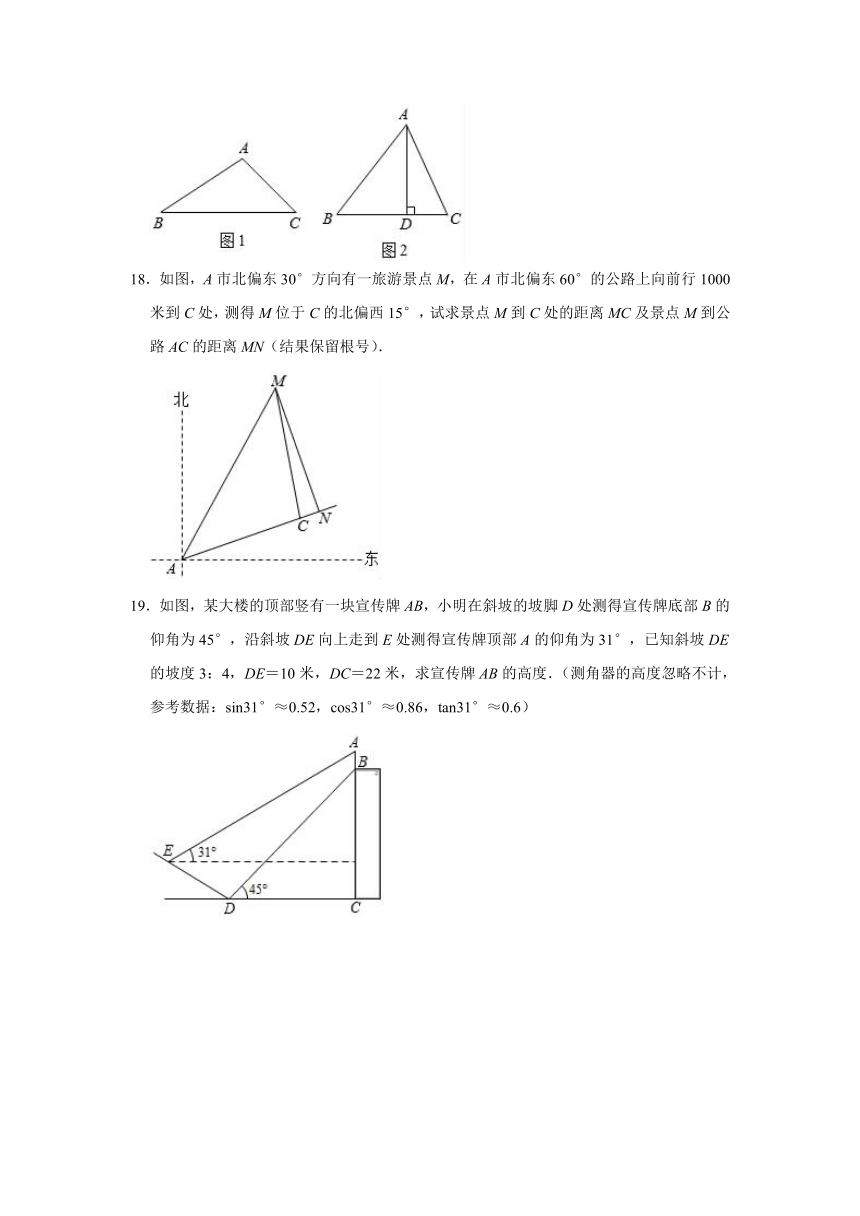
11.平放在地面上的三角形铁板ABC的一部分被沙堆掩埋,其示意图如图所示,量得∠A为54°,∠B为36°,边AB的长为2.1m,BC边上露出部分BD的长为0.9m,则铁板BC边被掩埋部分CD的长是
m.(结果精确到0.1m.参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38).
12.已知在△ABC中,∠C=90°,AB=6,BC=5,则sin∠A=
.
13.如图,在正方形网格中,小正方形的边长为1,点A,B,C,D都在格点上,AB与CD相交于点O,则∠AOC的正切值是
.
14.如图,海面上有一艘船由西向东航行,在A处测得正东方向上一座灯塔的最高点C的仰角为31°,在B处测得该灯塔的最高点C的仰角为45°,则∠ACB的度数为
.
15.如图,某河堤迎水坡AB的坡比i=1:,堤高BC=5m,则坡面AB的长是
m.
三.解答题
16.根据下列条件,解直角三角形:
(1)在Rt△ABC中,∠C=90°,a=2,b=2;
(2)在Rt△ABC中,∠C=90°,∠A=60°,c=6.
17.(1)如图1所示,△ABC中,∠B=30°,∠C=45°,AC=2,求AB和BC的长.
(2)如图2,△ABC中,AD⊥BC,垂足是D,若BC=14,AD=12,tan∠BAD=,求sinC的值.
18.如图,A市北偏东30°方向有一旅游景点M,在A市北偏东60°的公路上向前行1000米到C处,测得M位于C的北偏西15°,试求景点M到C处的距离MC及景点M到公路AC的距离MN(结果保留根号).
19.如图,某大楼的顶部竖有一块宣传牌AB,小明在斜坡的坡脚D处测得宣传牌底部B的仰角为45°,沿斜坡DE向上走到E处测得宣传牌顶部A的仰角为31°,已知斜坡DE的坡度3:4,DE=10米,DC=22米,求宣传牌AB的高度.(测角器的高度忽略不计,参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.6)
参考答案与试题解析
一.选择题
1.【解答】解:轮船以16海里/时的速度从港口A出发向北偏东63°方向航行,1小时后达到B处,
过点B作BC⊥从港口A出发向南偏东57°方向航行的航向于点C,
由题意得,AB=16海里,∠BAC=27°+33°=60°,
在Rt△ABC中,∠ACB=90°,∠BAC=60°,
∴AC=AB×cos∠BAC=8(海里),
∴另一轮船以8海里/时的速度同时从港口A出发向南偏东57°方向航行.离开港口1小时后,达到C处,
∴BC=AB×sin∠BAC=8(海里),
故选:A.
2.【解答】解:∵∠ABC=90°,
∴∠A+∠C=90°,
∵BD⊥AC,
∴∠ADB=90°,
∴∠A+∠ABD=90°,
∴∠ABD=∠C,
∵AB=2BC,
∴tan∠ABD=tan∠C==2,
故选:A.
3.【解答】解:连接BC,如图:
∵每个小正方形的边长均为1,
∴AB==,BC==,AC==,
∵AB2+BC2=AC2,
∴△ABC是直角三角形,
∴sin∠BAC===,
故选:B.
4.【解答】解:∵河坝横断面迎水坡AB的坡比为1:,坝高BC=4m,
∴=,
则AC=4(m),
故AB===4(m).
故选:C.
5.【解答】解:由题意得,∠AOB=90°﹣60°=30°,OA=300m,
∴AB=OA=150(m),
故选:C.
6.【解答】解:∵迎水坡AB的坡度i=1:,
∴=,即=,
解得,AC=10,
由勾股定理得,AB==20(m),
故选:C.
7.【解答】解:由题意可得,AB=BC=60×=30(海里),
在Rt△BCD中,∵∠BDC=90°,∠CBD=60°,
∴∠BCD=30°,
∴BD=BC=15(海里),
即点B、D之间的距离为15海里,
故选:B.
8.【解答】解:连接BC,
由题意可得:OB=OC=BC,
则△OBC是等边三角形,
故tan∠AOC=tan60°=.
故选:D.
9.【解答】解:延长AB交ED于G,过C作CF⊥DE于F,
∴GF=BC=5,
∵山坡CD的坡度为1:0.75,
∴设DF=3k,CF=4k,
∴CD=5k=35,
∴k=7,
∴DF=21,BG=CF=28,
∴EG=GF+DF+DE=5+21+19=45,
∵∠AED=52°,
∴AG=EGtan52°≈45×1.30=58.5,
∴AB=30.5米,
答:铁塔AB的高度约为30.5米.
故选:C.
10.【解答】解:过D作DF⊥AB于F,延长BE交CD于G,如图所示:
由题意得:∠ADF=14°,∠ABG=∠BGD=∠BFD=∠AFD=90°,
∴四边形BGDF是矩形,
∴BF=DG,DF=BG,
∵斜坡CE=2.6米,坡度为1:2.4,
∴CG=HE=1(米),EG=CH=2.4(米),
∴DF=BG=BE+EG=47.6+2.4=50(米),BF=DG=CD﹣CG=21﹣1=20(米),
在Rt△ADF中,tan∠ADF=,
∴AF=DF×tan14°≈50×0.25=12.5(米),
∴AB=AF+BF=12.5+20=32.5(米),
故选:B.
二.填空题(共5小题)
11.【解答】解:在直角三角形中,sinA=,
则BC=ABsinA=2.1sin54°≈2.1×0.81=1.701,
则CD=BC﹣BD=1.701﹣0.9,
=0.801≈0.8(m),
故答案为:0.8.
12.【解答】解:如图,
∵∠C=90°,BC=5,AB=6,
∴sinA==.
故答案为:.
13.【解答】解:如图取格点K,连接BK,过点K作KH⊥AB于H,如图所示:
∵DB=CK=2,DB∥CK,
∴四边形CDBK是平行四边形,
∴CD∥BK,
∴∠AOC=∠ABK,
过点K作KH⊥AB于H.
∵AB==,S△ABK=AK4=ABKH=20,
∴HK==,
∵BK==2,
∴BH===,
∴tan∠AOC=tan∠ABK===,
故答案为:.
14.【解答】解:由题意得:∠BAC=31°,∠CBD=45°,
∵∠CBD=∠BAC+∠ACB,
∴∠ACB=∠CBD﹣∠BAC=45°﹣31°=14°,
故答案为:14°.
15.【解答】解:∵坡比i=tan∠CAB===,∠ACB=90°,
∴∠BAC=30°,
∴AB=2BC,
又∵BC=5m,
∴AB=2BC=10m,
故答案为:10.
三.解答题(共4小题)
16.【解答】解:(1)在Rt△ABC中,∠C=90°,a=2,b=2,
∴c==4,
∴sinA==,sinB==,
∴∠A=60°,∠B=30°.
(2)在Rt△ABC中,∠C=90°,∠A=60°,c=6,
∴∠B=180°﹣∠A﹣∠C=30°,
∴sinA==,sinB==,
∴a=3,b=3.
17.【解答】解:(1)过点A作AH⊥BC于H.
∵∠AHC=90°,∠C=45°,
∴AH=HC=AC=,
∵∠B=30°,∠AHB=90°,
∴AB=2AH=2,
∴BH=AH=,
∴BC=BH+CH=+.
(2)在Rt△BAD中,∵tan∠BAD=,AD=12,
∴=,
∴BD=9,
∵BC=14,
∴CD=BC﹣BD=14﹣9=5,
∴AC===13,
∴sinC==.
18.【解答】解:由题意可知:∠MAC=60°﹣30°=30°,∠MCN=15°+60°=75°,
∴∠AMC=∠MCN﹣∠MAC=75°﹣30°=45°,
过C作CH⊥AM交AM于点H,如图所示:
在Rt△ACH中,∠MAC=30°,AC=1000m,
∴HCAC=500(m),AH=HC=500(m),
在Rt△HMC中,,
∴MN,
即:,
∴,
即MC的长度为米,MN的长度为米.
19.【解答】解:过E分别作CD、AC的垂线,设垂足为F、G,
则CF=EG,CG=EF,
在Rt△EFD中,∵斜坡DE的坡度3:4,DE=10米,
∴设EF=3x米,DF=4x米,
∴DE==5x=10,
∴x=2,
∴EF=6米,DF=8米,
在Rt△BCD中,∠BDC=45°,
∴BC=CD=22米,
∴BG=BC﹣CG=22﹣6=16(米),
在Rt△AEG中,AG=EGtan31°=30×0.6=18(米),
∴AB=AG﹣BG=18﹣16=2(米),
答:宣传牌AB的高度为2米.
一.选择题
1.已知,一轮船以16海里/时的速度从港口A出发向北偏东63°方向航行,另一轮船以8海里/时的速度同时从港口A出发向南偏东57°方向航行.离开港口1小时后,则两船相距( )
A.8海里
B.8海里
C.16海里
D.24海里
2.如图,在Rt△ABC中,∠ABC=90°,BD⊥AC于点D,AB=2BC,则tan∠ABD的值为( )
A.2
B.
C.
D.
3.如图,小正方形的边长均为1,A、B、C分别是小正方形的三个顶点,则sin∠BAC的值为( )
A.
B.
C.1
D.
4.如图,河坝横断面迎水坡AB的坡比为1:,坝高BC=4m,则AB的长度为( )
A.2m
B.4m
C.4m
D.6m
5.如图,小明在一条东西走向公路的O处,测得图书馆A在他的北偏东60°方向,且与他相距300m,则图书馆A到公路的距离AB为( )
A.150m
B.150m
C.150m
D.100m
6.如图,河堤横断面迎水坡AB的坡度i=1:,堤高BC=10m.则坡面AB的长度是( )
A.15m
B.20m
C.20m
D.10m
7.如图,一艘渔船从点A出发,沿正南方向航行了半小时到达点B,再沿南偏西60°方向航行了半小时到达点C,此时测得码头D在C的正东方向,该渔船的速度为60海里/时,则B,D两点间的距离为( )
A.10海里
B.15海里
C.30海里
D.90海里
8.如图,以O为圆心,任意长为半径画弧,与射线OA交于点B,再以B为圆心,BO长为半径画弧,两弧交于点C,画射线OC,则tan∠AOC的值为( )
A.
B.
C.
D.
9.国家电网近来实施了新一轮农村电网改造升级工程,解决了农村供电“最后1公里”问题,电力公司在改造时把某一输电线铁塔建在了一个坡度为1:0.75的山坡CD的平台BC上(如图),测得∠AED=52.5°,BC=5米,CD=35米,DE=19米,则铁塔AB的高度约为(参考数据:sin52.5°≈0.79,cos52.5°≈0.61,tan52.5°≈1.30)( )
A.7.6米
B.27.5米
C.30.5米
D.58.5米
10.如图,校园内有两栋教学楼求真楼AB和行知楼CD,已知CD的高度为21米,为测量AB的高度,小诚先在行知楼顶端D处测得求真楼顶端A处的仰角为14°,然后下楼从行知楼底部点C出发,先沿坡度为1:2.4的斜坡行走2.6米到达点E,再沿水平方向前进47.6米到达求真楼底端点B(A,B,C,D,E在同一平面内),则求真楼AB的高度约为( )
(参考数据:sin14°≈0.24,cos14°≈0.97,tan14°≈0.25)
A.31.5米
B.32.5米
C.33.5米
D.34.5米
二.填空题
11.平放在地面上的三角形铁板ABC的一部分被沙堆掩埋,其示意图如图所示,量得∠A为54°,∠B为36°,边AB的长为2.1m,BC边上露出部分BD的长为0.9m,则铁板BC边被掩埋部分CD的长是
m.(结果精确到0.1m.参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38).
12.已知在△ABC中,∠C=90°,AB=6,BC=5,则sin∠A=
.
13.如图,在正方形网格中,小正方形的边长为1,点A,B,C,D都在格点上,AB与CD相交于点O,则∠AOC的正切值是
.
14.如图,海面上有一艘船由西向东航行,在A处测得正东方向上一座灯塔的最高点C的仰角为31°,在B处测得该灯塔的最高点C的仰角为45°,则∠ACB的度数为
.
15.如图,某河堤迎水坡AB的坡比i=1:,堤高BC=5m,则坡面AB的长是
m.
三.解答题
16.根据下列条件,解直角三角形:
(1)在Rt△ABC中,∠C=90°,a=2,b=2;
(2)在Rt△ABC中,∠C=90°,∠A=60°,c=6.
17.(1)如图1所示,△ABC中,∠B=30°,∠C=45°,AC=2,求AB和BC的长.
(2)如图2,△ABC中,AD⊥BC,垂足是D,若BC=14,AD=12,tan∠BAD=,求sinC的值.
18.如图,A市北偏东30°方向有一旅游景点M,在A市北偏东60°的公路上向前行1000米到C处,测得M位于C的北偏西15°,试求景点M到C处的距离MC及景点M到公路AC的距离MN(结果保留根号).
19.如图,某大楼的顶部竖有一块宣传牌AB,小明在斜坡的坡脚D处测得宣传牌底部B的仰角为45°,沿斜坡DE向上走到E处测得宣传牌顶部A的仰角为31°,已知斜坡DE的坡度3:4,DE=10米,DC=22米,求宣传牌AB的高度.(测角器的高度忽略不计,参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.6)
参考答案与试题解析
一.选择题
1.【解答】解:轮船以16海里/时的速度从港口A出发向北偏东63°方向航行,1小时后达到B处,
过点B作BC⊥从港口A出发向南偏东57°方向航行的航向于点C,
由题意得,AB=16海里,∠BAC=27°+33°=60°,
在Rt△ABC中,∠ACB=90°,∠BAC=60°,
∴AC=AB×cos∠BAC=8(海里),
∴另一轮船以8海里/时的速度同时从港口A出发向南偏东57°方向航行.离开港口1小时后,达到C处,
∴BC=AB×sin∠BAC=8(海里),
故选:A.
2.【解答】解:∵∠ABC=90°,
∴∠A+∠C=90°,
∵BD⊥AC,
∴∠ADB=90°,
∴∠A+∠ABD=90°,
∴∠ABD=∠C,
∵AB=2BC,
∴tan∠ABD=tan∠C==2,
故选:A.
3.【解答】解:连接BC,如图:
∵每个小正方形的边长均为1,
∴AB==,BC==,AC==,
∵AB2+BC2=AC2,
∴△ABC是直角三角形,
∴sin∠BAC===,
故选:B.
4.【解答】解:∵河坝横断面迎水坡AB的坡比为1:,坝高BC=4m,
∴=,
则AC=4(m),
故AB===4(m).
故选:C.
5.【解答】解:由题意得,∠AOB=90°﹣60°=30°,OA=300m,
∴AB=OA=150(m),
故选:C.
6.【解答】解:∵迎水坡AB的坡度i=1:,
∴=,即=,
解得,AC=10,
由勾股定理得,AB==20(m),
故选:C.
7.【解答】解:由题意可得,AB=BC=60×=30(海里),
在Rt△BCD中,∵∠BDC=90°,∠CBD=60°,
∴∠BCD=30°,
∴BD=BC=15(海里),
即点B、D之间的距离为15海里,
故选:B.
8.【解答】解:连接BC,
由题意可得:OB=OC=BC,
则△OBC是等边三角形,
故tan∠AOC=tan60°=.
故选:D.
9.【解答】解:延长AB交ED于G,过C作CF⊥DE于F,
∴GF=BC=5,
∵山坡CD的坡度为1:0.75,
∴设DF=3k,CF=4k,
∴CD=5k=35,
∴k=7,
∴DF=21,BG=CF=28,
∴EG=GF+DF+DE=5+21+19=45,
∵∠AED=52°,
∴AG=EGtan52°≈45×1.30=58.5,
∴AB=30.5米,
答:铁塔AB的高度约为30.5米.
故选:C.
10.【解答】解:过D作DF⊥AB于F,延长BE交CD于G,如图所示:
由题意得:∠ADF=14°,∠ABG=∠BGD=∠BFD=∠AFD=90°,
∴四边形BGDF是矩形,
∴BF=DG,DF=BG,
∵斜坡CE=2.6米,坡度为1:2.4,
∴CG=HE=1(米),EG=CH=2.4(米),
∴DF=BG=BE+EG=47.6+2.4=50(米),BF=DG=CD﹣CG=21﹣1=20(米),
在Rt△ADF中,tan∠ADF=,
∴AF=DF×tan14°≈50×0.25=12.5(米),
∴AB=AF+BF=12.5+20=32.5(米),
故选:B.
二.填空题(共5小题)
11.【解答】解:在直角三角形中,sinA=,
则BC=ABsinA=2.1sin54°≈2.1×0.81=1.701,
则CD=BC﹣BD=1.701﹣0.9,
=0.801≈0.8(m),
故答案为:0.8.
12.【解答】解:如图,
∵∠C=90°,BC=5,AB=6,
∴sinA==.
故答案为:.
13.【解答】解:如图取格点K,连接BK,过点K作KH⊥AB于H,如图所示:
∵DB=CK=2,DB∥CK,
∴四边形CDBK是平行四边形,
∴CD∥BK,
∴∠AOC=∠ABK,
过点K作KH⊥AB于H.
∵AB==,S△ABK=AK4=ABKH=20,
∴HK==,
∵BK==2,
∴BH===,
∴tan∠AOC=tan∠ABK===,
故答案为:.
14.【解答】解:由题意得:∠BAC=31°,∠CBD=45°,
∵∠CBD=∠BAC+∠ACB,
∴∠ACB=∠CBD﹣∠BAC=45°﹣31°=14°,
故答案为:14°.
15.【解答】解:∵坡比i=tan∠CAB===,∠ACB=90°,
∴∠BAC=30°,
∴AB=2BC,
又∵BC=5m,
∴AB=2BC=10m,
故答案为:10.
三.解答题(共4小题)
16.【解答】解:(1)在Rt△ABC中,∠C=90°,a=2,b=2,
∴c==4,
∴sinA==,sinB==,
∴∠A=60°,∠B=30°.
(2)在Rt△ABC中,∠C=90°,∠A=60°,c=6,
∴∠B=180°﹣∠A﹣∠C=30°,
∴sinA==,sinB==,
∴a=3,b=3.
17.【解答】解:(1)过点A作AH⊥BC于H.
∵∠AHC=90°,∠C=45°,
∴AH=HC=AC=,
∵∠B=30°,∠AHB=90°,
∴AB=2AH=2,
∴BH=AH=,
∴BC=BH+CH=+.
(2)在Rt△BAD中,∵tan∠BAD=,AD=12,
∴=,
∴BD=9,
∵BC=14,
∴CD=BC﹣BD=14﹣9=5,
∴AC===13,
∴sinC==.
18.【解答】解:由题意可知:∠MAC=60°﹣30°=30°,∠MCN=15°+60°=75°,
∴∠AMC=∠MCN﹣∠MAC=75°﹣30°=45°,
过C作CH⊥AM交AM于点H,如图所示:
在Rt△ACH中,∠MAC=30°,AC=1000m,
∴HCAC=500(m),AH=HC=500(m),
在Rt△HMC中,,
∴MN,
即:,
∴,
即MC的长度为米,MN的长度为米.
19.【解答】解:过E分别作CD、AC的垂线,设垂足为F、G,
则CF=EG,CG=EF,
在Rt△EFD中,∵斜坡DE的坡度3:4,DE=10米,
∴设EF=3x米,DF=4x米,
∴DE==5x=10,
∴x=2,
∴EF=6米,DF=8米,
在Rt△BCD中,∠BDC=45°,
∴BC=CD=22米,
∴BG=BC﹣CG=22﹣6=16(米),
在Rt△AEG中,AG=EGtan31°=30×0.6=18(米),
∴AB=AG﹣BG=18﹣16=2(米),
答:宣传牌AB的高度为2米.
