人教版数学九年级下册 29.3课题学习 制作立体模型同步测试试题(一)(Word版 含解析)
文档属性
| 名称 | 人教版数学九年级下册 29.3课题学习 制作立体模型同步测试试题(一)(Word版 含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 238.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 20:13:37 | ||
图片预览


文档简介
课题学习
制作立体模型同步测试试题(一)
一.选择题
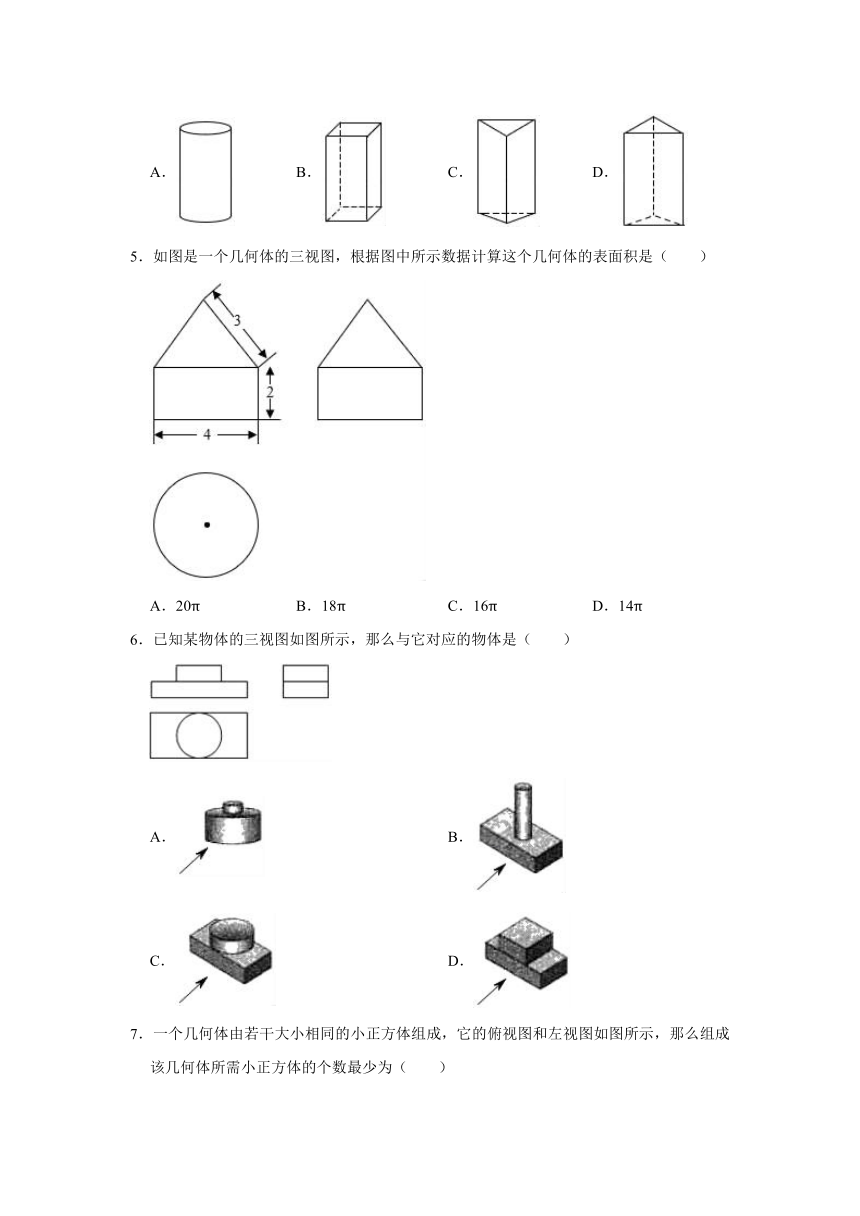
1.图中为某几何体的分别从上面、前面、左边看到的三个图形,该几何体是( )
A.圆锥
B.圆柱
C.正三棱柱
D.正三棱锥
2.如图,是由大小一样的小立方块摆成的立体图形的三视图,则摆成这个立体图形所需的小立方块的个数为( )
A.3
B.4
C.5
D.6
3.如图,某糕点包装盒的俯视图是正五边形,则正五边形的每一内角的度数为( )
A.72°
B.108°
C.120°
D.540°
4.如图,是一个几何体的主视图和左视图,则这个几何体可能为( )
A.
B.
C.
D.
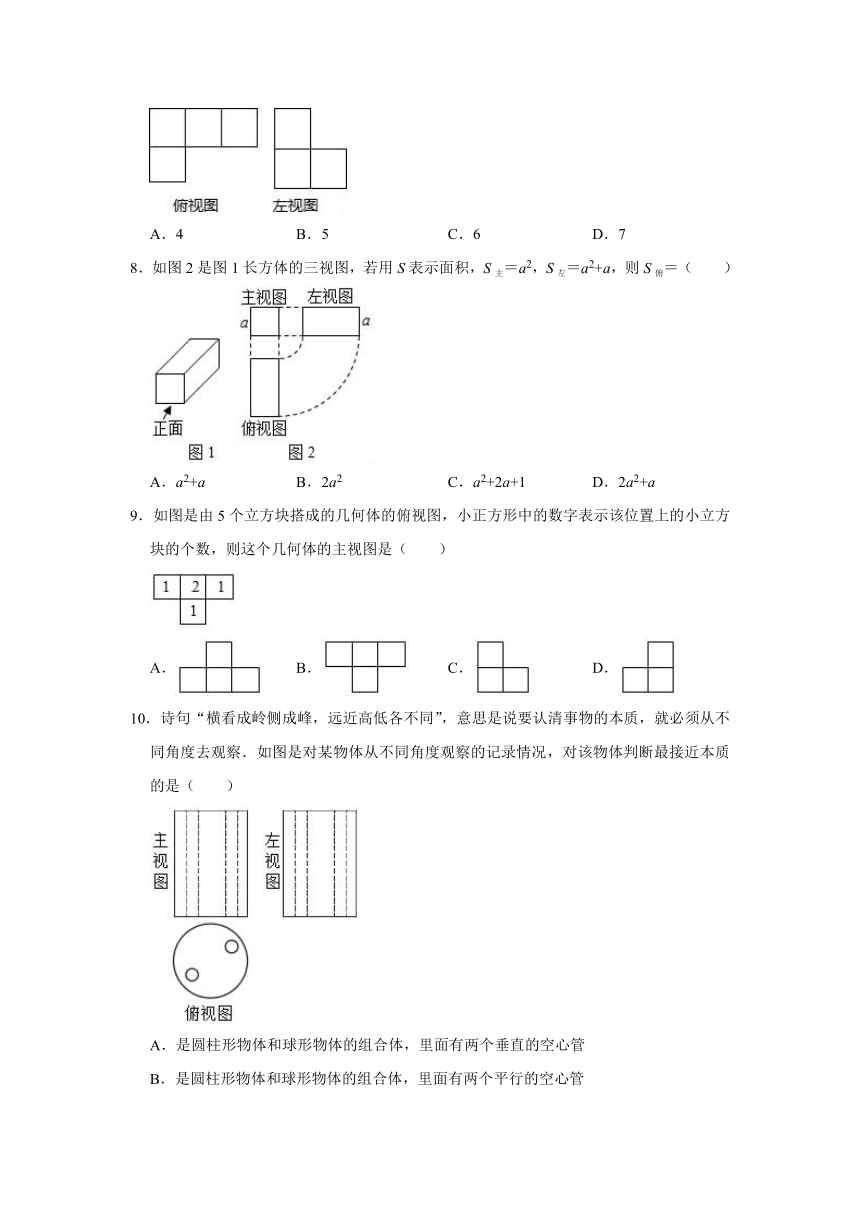
5.如图是一个几何体的三视图,根据图中所示数据计算这个几何体的表面积是( )
A.20π
B.18π
C.16π
D.14π
6.已知某物体的三视图如图所示,那么与它对应的物体是( )
A.
B.
C.
D.
7.一个几何体由若干大小相同的小正方体组成,它的俯视图和左视图如图所示,那么组成该几何体所需小正方体的个数最少为( )
A.4
B.5
C.6
D.7
8.如图2是图1长方体的三视图,若用S表示面积,S主=a2,S左=a2+a,则S俯=( )
A.a2+a
B.2a2
C.a2+2a+1
D.2a2+a
9.如图是由5个立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上的小立方块的个数,则这个几何体的主视图是( )
A.
B.
C.
D.
10.诗句“横看成岭侧成峰,远近高低各不同”,意思是说要认清事物的本质,就必须从不同角度去观察.如图是对某物体从不同角度观察的记录情况,对该物体判断最接近本质的是( )
A.是圆柱形物体和球形物体的组合体,里面有两个垂直的空心管
B.是圆柱形物体和球形物体的组合体,里面有两个平行的空心管
C.是圆柱形物体,里面有两个垂直的空心管
D.是圆柱形物体,里面有两个平行的空心管
二.填空题
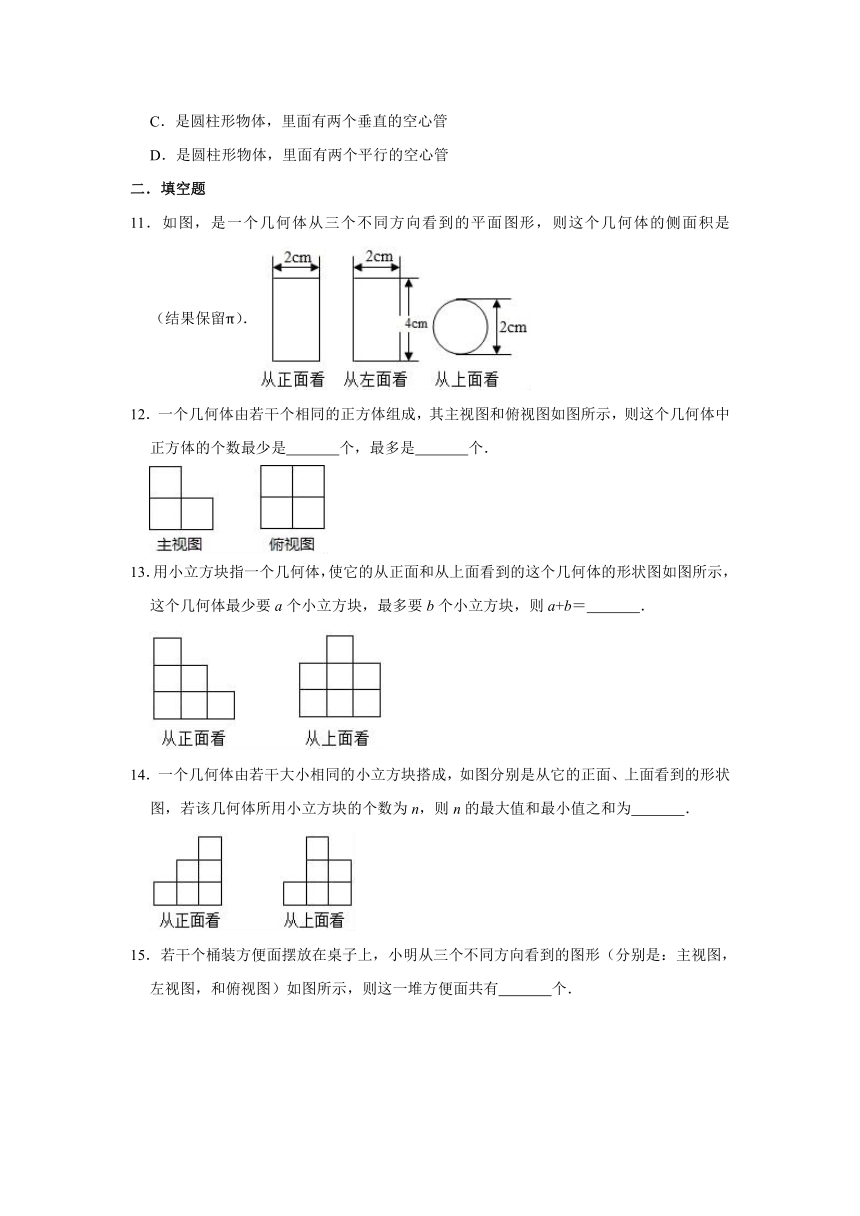
11.如图,是一个几何体从三个不同方向看到的平面图形,则这个几何体的侧面积是
(结果保留π).
12.一个几何体由若干个相同的正方体组成,其主视图和俯视图如图所示,则这个几何体中正方体的个数最少是
个,最多是
个.
13.用小立方块指一个几何体,使它的从正面和从上面看到的这个几何体的形状图如图所示,这个几何体最少要a个小立方块,最多要b个小立方块,则a+b=
.
14.一个几何体由若干大小相同的小立方块搭成,如图分别是从它的正面、上面看到的形状图,若该几何体所用小立方块的个数为n,则n的最大值和最小值之和为
.
15.若干个桶装方便面摆放在桌子上,小明从三个不同方向看到的图形(分别是:主视图,左视图,和俯视图)如图所示,则这一堆方便面共有
个.
三.解答题
16.如图是由若干个相同的小正方体组成的几何体从正面、上面看到的形状图.
(1)组成这个物体的小正方体的个数可能是多少?
(2)求这个几何体的最大表面积.
17.如图是分别从正面、左面、上面观察一个几何体得到的图形,请解答以下问题:
(1)这个几何体的名称为
;
(2)若从正面看到的是长方形,其长为10cm;从上面看到的是等边三角形,其边长为4cm,求这个几何体的侧面积.
18.如图,已知一个几何体的主视图与俯视图,求该几何体的体积.(π取3.14,单位:cm)
19.如图①是一个组合几何体,右边是它的两种视图,在右边横线上填写出两种视图名称;根据两种视图中尺寸,计算这个组合几何体的表面积和体积.
参考答案与试题解析
一.选择题
1.【解答】解:根据主视图和左视图为矩形判断出是柱体,根据俯视图是三角形可判断出这个几何体应该是正三棱柱.
故选:C.
2.【解答】解:由俯视图易得最底层有2个正方体,第二层有1个正方体,
那么共有2+1=3个正方体组成.
故选:A.
3.【解答】解:∵正多边形的内角和公式为:(n﹣2)×180°,
∴正五边形的内角和是:(5﹣2)×180°=540°,
则每个内角是:540°÷5=108°.
故选:B.
4.【解答】解:分别画出各个几何体的主视图和左视图,
故选:B.
5.【解答】解:这个几何体的表面积=π22+π32+2π22=18π,
故选:B.
6.【解答】解:由三视图知,该几何体是下面是长方体,上面是一个圆柱体,且长方体的宽与圆柱底面直径相等,
符合这一条件的是C选项几何体,
故选:C.
7.【解答】解:由俯视图与左视图知,该几何体所需小正方体个数最少分布情况如下图所示:
所以组成该几何体所需小正方体的个数最少为5,
故选:B.
8.【解答】解:∵,
∴俯视图的长为a+1,宽为a,
∴,
故选:A.
9.【解答】解:从正面看去,一共三列,左边有1个小正方形,中间有2个小正方形,右边有1个小正方形,主视图是.
故选:A.
10.【解答】解:由图可得,该物体是圆柱形物体,里面有两个平行的空心管,
故选:D.
二.填空题(共5小题)
11.【解答】解:该几何体是圆柱.
其侧面积为:π×2×4=8π(cm2).
答:这个几何体的侧面积是8πcm2.
故答案为:8πcm2.
12.【解答】解:综合俯视图和主视图,这个几何体的左边一列最少有3个正方体,最多有4个正方体,右边一列有2个正方体,
所以这个几何体中正方体的个数最少是5个,最多是6个.
故答案为:5;6.
13.【解答】解:由主视图和俯视图可知,第1列小立方体的个数最多为6,最少为4;第2列小立方体的个数最多为6,最少为4;第3列小正方体的个数为2;
则a=4+4+2=10,b=6+6+2=14;
则a+b=10+14=24.
故答案为:24.
14.【解答】解:根据主视图、俯视图,可以得出最少时、最多时,在俯视图的相应位置上所摆放的个数如下:
最少时需要9个,最多时需要13个,
因此n=9+13=22,
故答案为:22.
15.【解答】解:根据三视图的形状,可得到,俯视图上每个位置上放置的个数,进而得出总数量,
俯视图中的数,表示该位置放的数量,
故这一堆方便面共有2+2+1=5(个).
故答案为:5.
三.解答题(共4小题)
16.【解答】解:(1)组成这个物体的小正方体的个数可能是4或5;
(2)这个几何体的最大表面积是3×2+3×2+5×2=22.
17.【解答】解:(1)这个几何体是三棱柱.
故答案为:三棱柱;
(2)三棱柱的侧面展开图形是长方形,长方形的长是等边三角形的周长,宽是三棱柱的高,
所以三棱柱侧面展开图形的面积为:
S=3×4×10=120(cm2).
答:这个几何体的侧面积为120cm2.
18.【解答】解:3.14×(20÷2)2×32+30×25×40
=3.14×100×32+30000
=10048+30000
=40048(cm3).
故该几何体的体积是40048cm3.
19.【解答】解:两个视图分别为主视图、俯视图,
体积为:8×5×2+π×22×6=80+24π,
表面积为:(8×5+8×2+5×2)×2+4π×6=132+24π,
答:这个几何体的表面积为132+24π,体积为80+24π.
制作立体模型同步测试试题(一)
一.选择题
1.图中为某几何体的分别从上面、前面、左边看到的三个图形,该几何体是( )
A.圆锥
B.圆柱
C.正三棱柱
D.正三棱锥
2.如图,是由大小一样的小立方块摆成的立体图形的三视图,则摆成这个立体图形所需的小立方块的个数为( )
A.3
B.4
C.5
D.6
3.如图,某糕点包装盒的俯视图是正五边形,则正五边形的每一内角的度数为( )
A.72°
B.108°
C.120°
D.540°
4.如图,是一个几何体的主视图和左视图,则这个几何体可能为( )
A.
B.
C.
D.
5.如图是一个几何体的三视图,根据图中所示数据计算这个几何体的表面积是( )
A.20π
B.18π
C.16π
D.14π
6.已知某物体的三视图如图所示,那么与它对应的物体是( )
A.
B.
C.
D.
7.一个几何体由若干大小相同的小正方体组成,它的俯视图和左视图如图所示,那么组成该几何体所需小正方体的个数最少为( )
A.4
B.5
C.6
D.7
8.如图2是图1长方体的三视图,若用S表示面积,S主=a2,S左=a2+a,则S俯=( )
A.a2+a
B.2a2
C.a2+2a+1
D.2a2+a
9.如图是由5个立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上的小立方块的个数,则这个几何体的主视图是( )
A.
B.
C.
D.
10.诗句“横看成岭侧成峰,远近高低各不同”,意思是说要认清事物的本质,就必须从不同角度去观察.如图是对某物体从不同角度观察的记录情况,对该物体判断最接近本质的是( )
A.是圆柱形物体和球形物体的组合体,里面有两个垂直的空心管
B.是圆柱形物体和球形物体的组合体,里面有两个平行的空心管
C.是圆柱形物体,里面有两个垂直的空心管
D.是圆柱形物体,里面有两个平行的空心管
二.填空题
11.如图,是一个几何体从三个不同方向看到的平面图形,则这个几何体的侧面积是
(结果保留π).
12.一个几何体由若干个相同的正方体组成,其主视图和俯视图如图所示,则这个几何体中正方体的个数最少是
个,最多是
个.
13.用小立方块指一个几何体,使它的从正面和从上面看到的这个几何体的形状图如图所示,这个几何体最少要a个小立方块,最多要b个小立方块,则a+b=
.
14.一个几何体由若干大小相同的小立方块搭成,如图分别是从它的正面、上面看到的形状图,若该几何体所用小立方块的个数为n,则n的最大值和最小值之和为
.
15.若干个桶装方便面摆放在桌子上,小明从三个不同方向看到的图形(分别是:主视图,左视图,和俯视图)如图所示,则这一堆方便面共有
个.
三.解答题
16.如图是由若干个相同的小正方体组成的几何体从正面、上面看到的形状图.
(1)组成这个物体的小正方体的个数可能是多少?
(2)求这个几何体的最大表面积.
17.如图是分别从正面、左面、上面观察一个几何体得到的图形,请解答以下问题:
(1)这个几何体的名称为
;
(2)若从正面看到的是长方形,其长为10cm;从上面看到的是等边三角形,其边长为4cm,求这个几何体的侧面积.
18.如图,已知一个几何体的主视图与俯视图,求该几何体的体积.(π取3.14,单位:cm)
19.如图①是一个组合几何体,右边是它的两种视图,在右边横线上填写出两种视图名称;根据两种视图中尺寸,计算这个组合几何体的表面积和体积.
参考答案与试题解析
一.选择题
1.【解答】解:根据主视图和左视图为矩形判断出是柱体,根据俯视图是三角形可判断出这个几何体应该是正三棱柱.
故选:C.
2.【解答】解:由俯视图易得最底层有2个正方体,第二层有1个正方体,
那么共有2+1=3个正方体组成.
故选:A.
3.【解答】解:∵正多边形的内角和公式为:(n﹣2)×180°,
∴正五边形的内角和是:(5﹣2)×180°=540°,
则每个内角是:540°÷5=108°.
故选:B.
4.【解答】解:分别画出各个几何体的主视图和左视图,
故选:B.
5.【解答】解:这个几何体的表面积=π22+π32+2π22=18π,
故选:B.
6.【解答】解:由三视图知,该几何体是下面是长方体,上面是一个圆柱体,且长方体的宽与圆柱底面直径相等,
符合这一条件的是C选项几何体,
故选:C.
7.【解答】解:由俯视图与左视图知,该几何体所需小正方体个数最少分布情况如下图所示:
所以组成该几何体所需小正方体的个数最少为5,
故选:B.
8.【解答】解:∵,
∴俯视图的长为a+1,宽为a,
∴,
故选:A.
9.【解答】解:从正面看去,一共三列,左边有1个小正方形,中间有2个小正方形,右边有1个小正方形,主视图是.
故选:A.
10.【解答】解:由图可得,该物体是圆柱形物体,里面有两个平行的空心管,
故选:D.
二.填空题(共5小题)
11.【解答】解:该几何体是圆柱.
其侧面积为:π×2×4=8π(cm2).
答:这个几何体的侧面积是8πcm2.
故答案为:8πcm2.
12.【解答】解:综合俯视图和主视图,这个几何体的左边一列最少有3个正方体,最多有4个正方体,右边一列有2个正方体,
所以这个几何体中正方体的个数最少是5个,最多是6个.
故答案为:5;6.
13.【解答】解:由主视图和俯视图可知,第1列小立方体的个数最多为6,最少为4;第2列小立方体的个数最多为6,最少为4;第3列小正方体的个数为2;
则a=4+4+2=10,b=6+6+2=14;
则a+b=10+14=24.
故答案为:24.
14.【解答】解:根据主视图、俯视图,可以得出最少时、最多时,在俯视图的相应位置上所摆放的个数如下:
最少时需要9个,最多时需要13个,
因此n=9+13=22,
故答案为:22.
15.【解答】解:根据三视图的形状,可得到,俯视图上每个位置上放置的个数,进而得出总数量,
俯视图中的数,表示该位置放的数量,
故这一堆方便面共有2+2+1=5(个).
故答案为:5.
三.解答题(共4小题)
16.【解答】解:(1)组成这个物体的小正方体的个数可能是4或5;
(2)这个几何体的最大表面积是3×2+3×2+5×2=22.
17.【解答】解:(1)这个几何体是三棱柱.
故答案为:三棱柱;
(2)三棱柱的侧面展开图形是长方形,长方形的长是等边三角形的周长,宽是三棱柱的高,
所以三棱柱侧面展开图形的面积为:
S=3×4×10=120(cm2).
答:这个几何体的侧面积为120cm2.
18.【解答】解:3.14×(20÷2)2×32+30×25×40
=3.14×100×32+30000
=10048+30000
=40048(cm3).
故该几何体的体积是40048cm3.
19.【解答】解:两个视图分别为主视图、俯视图,
体积为:8×5×2+π×22×6=80+24π,
表面积为:(8×5+8×2+5×2)×2+4π×6=132+24π,
答:这个几何体的表面积为132+24π,体积为80+24π.
