6.4数据的离散程度-北师大版八年级数学上册假期同步测试(Word版含答案)
文档属性
| 名称 | 6.4数据的离散程度-北师大版八年级数学上册假期同步测试(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 164.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 08:09:22 | ||
图片预览



文档简介
北师大版八年级数学上册第六章6.4数据的离散程度 同步测试
一.选择题
1.随着长株潭一体化进程不断推进,湘潭在交通方面越来越让人期待.将要实施的“两干一轨”项目中的“一轨”,是将长沙市地铁3号线南延至湘潭北站,往返长潭两地又将多“地铁”这一选择.为了解人们选择交通工具的意愿,随机抽取了部分市民进行调查,并根据调查结果绘制如下统计图,关于交通工具选择的人数数据,以下结论正确的是( )
A.平均数是8 B.众数是11 C.中位数是2 D.极差是10
2.在一次艺术作品制作比赛中,某小组八件作品的成绩(单位:分)分别是:7、9、8、9、8、10、9、7,下列说法不正确的是( )
A.中位数是8.5 B.平均数是8.4
C.众数是9 D.极差是3
3.压岁钱由来已久,古称“厌胜钱”、“压祟钱”等.铛铛同学在2019年春节共收到10位长辈给的压岁钱,分别是:100元、200元、100元、50元、400元、300元、50元、100元、200元、400元,关于这组数据,下列说法正确的是( )
A.中位数是200元 B.众数是100元
C.平均数是200元 D.极差是300元
4.一组数据﹣3,a,5,3,b,其中a>0,b>0,平均数为3,极差为10,则这组数据的众数为( )
A.7 B.5 C.3 D.﹣3
5.一组数据3,﹣2,8,3,x的极差是10,那么x的取值有( )
A.1个 B.2个 C.3个 D.无数个
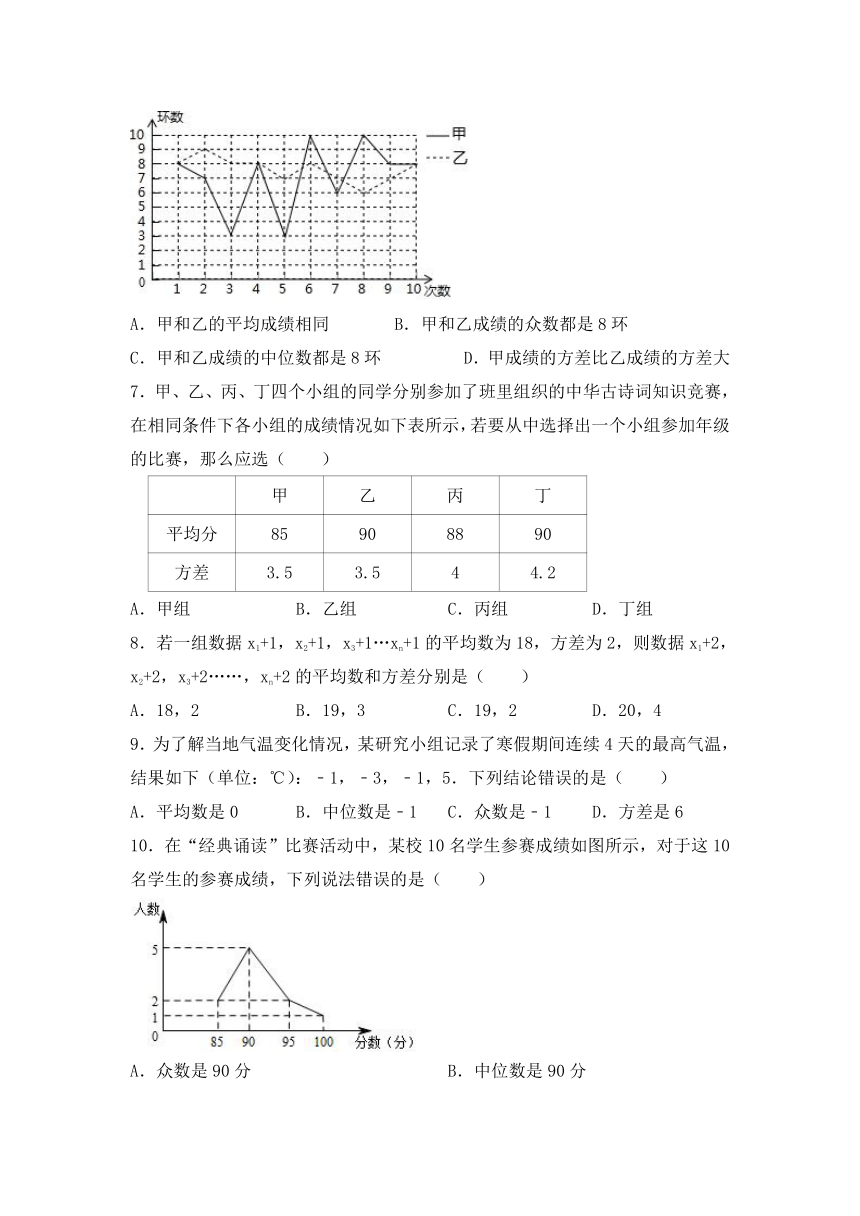
6.如图是甲、乙两人射击成绩的统计图,两人都射击了10次,下列说法错误的是( )
A.甲和乙的平均成绩相同 B.甲和乙成绩的众数都是8环
C.甲和乙成绩的中位数都是8环 D.甲成绩的方差比乙成绩的方差大
7.甲、乙、丙、丁四个小组的同学分别参加了班里组织的中华古诗词知识竞赛,在相同条件下各小组的成绩情况如下表所示,若要从中选择出一个小组参加年级的比赛,那么应选( )
甲 乙 丙 丁
平均分 85 90 88 90
方差 3.5 3.5 4 4.2
A.甲组 B.乙组 C.丙组 D.丁组
8.若一组数据x1+1,x2+1,x3+1…xn+1的平均数为18,方差为2,则数据x1+2,x2+2,x3+2……,xn+2的平均数和方差分别是( )
A.18,2 B.19,3 C.19,2 D.20,4
9.为了解当地气温变化情况,某研究小组记录了寒假期间连续4天的最高气温,结果如下(单位:℃):﹣1,﹣3,﹣1,5.下列结论错误的是( )
A.平均数是0 B.中位数是﹣1 C.众数是﹣1 D.方差是6
10.在“经典诵读”比赛活动中,某校10名学生参赛成绩如图所示,对于这10名学生的参赛成绩,下列说法错误的是( )
A.众数是90分 B.中位数是90分
C.平均数是91分 D.方差是1
11.已知数据1,2,3,3,4,5,则下列关于这组数据的说法,错误的是( )
A.平均数是3 B.中位数和众数都是3
C.方差为10 D.标准差是
12.一样本的各数据都减少4,则新数据的( )
A.平均数与标准差都不变 B.平均数减少4,标准差减少2
C.平均数减少4,标准差不变 D.平均数减少4,方差减少2
二.填空题
13.一组数据﹣1,0,2,4,x的极差为7,则x= .
14.已知一组数据的标准差是2,则这组数据的方差是 .
15.甲、乙两人各进行10次射击比赛,平均成绩均为9环,方差分别是:S甲2=2,S乙2=4,则射击成绩较稳定的是 (选填“甲”或“乙”).
16.如果一组数据x1,x2,x3,x4,x5的方差是1,那么数x1﹣10,x2﹣10,x3﹣10,x4﹣10,x5﹣10的方差是 .
17.已知数据3,2,4,6,5,则这组数据的方差是 .
18.已知一组数据x1,x2,x3的平均数和方差分别为5和2,则数据x1+1,x2+1,x3+1的平均数是 ,标准差是 .
19.某样本方差的计算公式是S2=[(x1﹣3)2+(x2﹣3)2+…+(x16﹣3)2],则它的样本容量是 ,样本的平均数是 ,样本的平方和是176时,标准差是 .
20.一组数据2,4,5,1,a的平均数为a,这组数据的方差为 .
三.解答题
21.我市开展了“寻找雷锋足迹”的活动,某中学为了了解七年级800名学生在“学雷锋活动月”中做好事的情况,随机调查了七年级50名学生在一个月内做好事的次数,并将所得数据绘制成统计图,请根据图中提供的信息解答下列问题:
①本次抽样调查的样本容量是 ,样本平均数是 ,众数是 ,极差是 :
②根据样本数据,估计该校七年级800名学生在“学雷锋活动月”中做好事不少于4次的人数.
22.武侯区某学校开展了该校八年级部分学生的综合素质测评活动,随机选取了该校八年级的50名学生进行测评,统计数据如下表:
测评成绩 (单位:分) 80 85 90 95 100
人数 5 10 10 20 5
(1)这50名学生的测评成绩的众数是 分,中位数是 分,极差是 分;
(2)求这50名学生的测评成绩的平均数;
(3)若该校八年级共有学生300名,测评成绩在90分以上(包含90分)为优秀,试估计该校八年级优秀学生共有多少名?
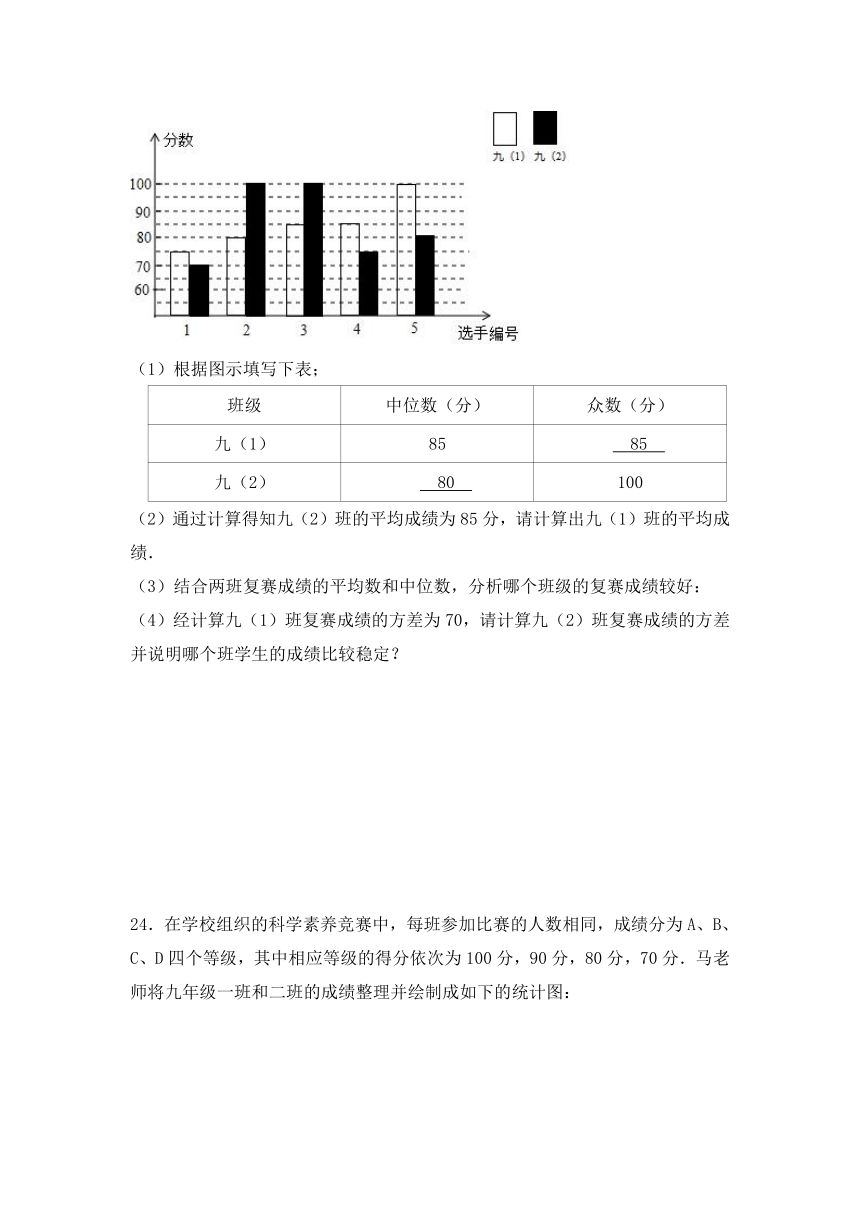
23.某中学开展“唱歌”比赛活动,九年级(1)、(2)班各选出5名选手参加复赛,5名选手的复赛成绩(满分为100分)如图所示:
(1)根据图示填写下表;
班级 中位数(分) 众数(分)
九(1) 85 85
九(2) 80 100
(2)通过计算得知九(2)班的平均成绩为85分,请计算出九(1)班的平均成绩.
(3)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好:
(4)经计算九(1)班复赛成绩的方差为70,请计算九(2)班复赛成绩的方差并说明哪个班学生的成绩比较稳定?
24.在学校组织的科学素养竞赛中,每班参加比赛的人数相同,成绩分为A、B、C、D四个等级,其中相应等级的得分依次为100分,90分,80分,70分.马老师将九年级一班和二班的成绩整理并绘制成如下的统计图:
请你根据以上提供的信息解答下列问题:
(1)此次竞赛中二班成绩在80分及其以上的人数是 人;
(2)求出下表中a、b、c的值;
平均数(分) 中位数(分) 众数(分) 方差
一班 87.6 b 90 106.24
二班 a 80 c 138.24
(3)学校准备在这两个班中选一个班参加市级科学素养竞赛,你建议学校选哪个班参加?说说你的理由.
25.甲、乙两名同学进入八年级后某科6次考试成绩如图所示:
平均数 方差 中位数 众数
甲 75 75
乙 33.3 70
(1)请根据图填写上表;
(2)从平均数和方差结合看,你认为谁的成绩稳定性更好些?
26.某市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了四次测试,测试成绩如表(单位:环):
第一次 第二次 第三次 第四次
甲 9 8 8 7
乙 10 6 7 9
(1)根据表格中的数据,分别计算甲、乙两名运动员的平均成绩;
(2)分别计算甲、乙两人四次测试成绩的方差;根据计算的结果,你认为推荐谁参加省比赛更合适?请说明理由.
27.一次期中考试中,A、B、C、D、E五位同学的数学、语文成绩等有关信息如下表所示:(单位:分)
A B C D E 极差 平均数 标准差
数学 71 72 69 68 70 70
语文 88 82 94 85 76 18 85
其中,表格中的“标准差”是方差的算术平方根.
(1)填写表格中的空档;
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式是:标准分=(个人成绩一平均成绩)÷成绩标准差.从标准分看,标准分大的考试成绩更好.请问A同学在本次考试中,数学与语文哪个学科考得更好?
答案提示
1.A.2.B.3.B.4.C.5.D.6.A.7.B.8.C.9.D.10.D.11.C.12.C.
13.6或﹣3. 14.4. 15.甲. 16.1. 17.2. 18.6,.19. 16,3,. 20.2.
21.解:①根据题意知,样本容量为50;平均数(2×5+3×6+4×13+5×16+6×10)÷50=4.4次;
众数:5次;极差:6﹣2=4次,
故答案为:50、4.4次、5次、4次;
②估计做好事不少于4次的人数:800×=624人.
22.解:(1)这50名学生的测评成绩的众数是95分,中位数是分,极差是100﹣80=20分;
(2)这50名学生的测评成绩的平均数是=91分;
(3)该校八年级优秀学生共有300×=210人,
故答案为:(1)95;92.5;20
23.解:(1)九(1)众数为85分,九(2)班的中位数为80分,
故答案为:80,85;
(2)(分);
(3)从平均数上看,均为85(分),水平相当,
从中位数上看,(1)班85(分)(2)班80分,(1)班好于(2)班,
所以(1)班较好.
(4)=,
∵70<160,
∴(1)班稳定.
24.解:(1)此次竞赛中二班成绩在80分及其以上的人数是:(6+12+2+5)×(1﹣16%)=21(人),
故答案为:21;
(2)由一班竞赛成绩统计图可知,b=90,
二班参加的总人数和一班一样多,二班参加的人数是:6+12+2+5=25,
a=100×44%+90×4%+80×36%+70×16%=87.6,
c=100,
即a=87.6,b=90,c=100;
(3)选择一班参加,
理由:由表格可知,两个班的平均数相同,但一班的中位数高于二班,并且一班的方差小于二班,学生成绩发挥比较稳定,故选择一班.
25.解:(1)乙的平均数:=(85+70+70+75+70+80)=75分,
S=[(60﹣75)2+(65﹣75)2+(75﹣75)2+(75﹣75)2+(80﹣75)2+(95﹣75)2]=125,
乙的中位数为:(70+75)÷2=72.5,甲的众数75,乙的众数为70,
填写表格如下:
平均数 方差 中位数 众数
甲 75 125 75 75
乙 75 33.3 72.5 70
故答案为:75,125,72,5,75;
(2)从平均数上看家、乙两人的成绩相同,但乙的方差较小,说明乙的成绩比较稳定,单从是否稳定上看,乙的成绩较稳定.
26.解:(1)甲的平均成绩是:
(9+8+8+7)÷4=8,
乙的平均成绩是:
(10+6+7+9)÷4=8,
(2)甲的方差是:
[(9﹣8)2+(8﹣8)2+(8﹣8)2+(7﹣8)2]=,
乙的方差是:
[(10﹣8)2+(6﹣8)2+(7﹣8)2+(9﹣8)2]=.
所以推荐甲参加省比赛更合适.理由如下:
两人的平均成绩相等,说明实力相当;
但是甲的四次测试成绩的方差比乙小,说明甲发挥较为稳定,
故推荐甲参加省比赛更合适.
27.解:(1)极差=72﹣68=4,平均分=(71+72+…+70)÷5=70,标准差=6,
故答案为:4;6;
(2)∵数学标准分=,英语标准分=0.5,
∴数学更好.
一.选择题
1.随着长株潭一体化进程不断推进,湘潭在交通方面越来越让人期待.将要实施的“两干一轨”项目中的“一轨”,是将长沙市地铁3号线南延至湘潭北站,往返长潭两地又将多“地铁”这一选择.为了解人们选择交通工具的意愿,随机抽取了部分市民进行调查,并根据调查结果绘制如下统计图,关于交通工具选择的人数数据,以下结论正确的是( )
A.平均数是8 B.众数是11 C.中位数是2 D.极差是10
2.在一次艺术作品制作比赛中,某小组八件作品的成绩(单位:分)分别是:7、9、8、9、8、10、9、7,下列说法不正确的是( )
A.中位数是8.5 B.平均数是8.4
C.众数是9 D.极差是3
3.压岁钱由来已久,古称“厌胜钱”、“压祟钱”等.铛铛同学在2019年春节共收到10位长辈给的压岁钱,分别是:100元、200元、100元、50元、400元、300元、50元、100元、200元、400元,关于这组数据,下列说法正确的是( )
A.中位数是200元 B.众数是100元
C.平均数是200元 D.极差是300元
4.一组数据﹣3,a,5,3,b,其中a>0,b>0,平均数为3,极差为10,则这组数据的众数为( )
A.7 B.5 C.3 D.﹣3
5.一组数据3,﹣2,8,3,x的极差是10,那么x的取值有( )
A.1个 B.2个 C.3个 D.无数个
6.如图是甲、乙两人射击成绩的统计图,两人都射击了10次,下列说法错误的是( )
A.甲和乙的平均成绩相同 B.甲和乙成绩的众数都是8环
C.甲和乙成绩的中位数都是8环 D.甲成绩的方差比乙成绩的方差大
7.甲、乙、丙、丁四个小组的同学分别参加了班里组织的中华古诗词知识竞赛,在相同条件下各小组的成绩情况如下表所示,若要从中选择出一个小组参加年级的比赛,那么应选( )
甲 乙 丙 丁
平均分 85 90 88 90
方差 3.5 3.5 4 4.2
A.甲组 B.乙组 C.丙组 D.丁组
8.若一组数据x1+1,x2+1,x3+1…xn+1的平均数为18,方差为2,则数据x1+2,x2+2,x3+2……,xn+2的平均数和方差分别是( )
A.18,2 B.19,3 C.19,2 D.20,4
9.为了解当地气温变化情况,某研究小组记录了寒假期间连续4天的最高气温,结果如下(单位:℃):﹣1,﹣3,﹣1,5.下列结论错误的是( )
A.平均数是0 B.中位数是﹣1 C.众数是﹣1 D.方差是6
10.在“经典诵读”比赛活动中,某校10名学生参赛成绩如图所示,对于这10名学生的参赛成绩,下列说法错误的是( )
A.众数是90分 B.中位数是90分
C.平均数是91分 D.方差是1
11.已知数据1,2,3,3,4,5,则下列关于这组数据的说法,错误的是( )
A.平均数是3 B.中位数和众数都是3
C.方差为10 D.标准差是
12.一样本的各数据都减少4,则新数据的( )
A.平均数与标准差都不变 B.平均数减少4,标准差减少2
C.平均数减少4,标准差不变 D.平均数减少4,方差减少2
二.填空题
13.一组数据﹣1,0,2,4,x的极差为7,则x= .
14.已知一组数据的标准差是2,则这组数据的方差是 .
15.甲、乙两人各进行10次射击比赛,平均成绩均为9环,方差分别是:S甲2=2,S乙2=4,则射击成绩较稳定的是 (选填“甲”或“乙”).
16.如果一组数据x1,x2,x3,x4,x5的方差是1,那么数x1﹣10,x2﹣10,x3﹣10,x4﹣10,x5﹣10的方差是 .
17.已知数据3,2,4,6,5,则这组数据的方差是 .
18.已知一组数据x1,x2,x3的平均数和方差分别为5和2,则数据x1+1,x2+1,x3+1的平均数是 ,标准差是 .
19.某样本方差的计算公式是S2=[(x1﹣3)2+(x2﹣3)2+…+(x16﹣3)2],则它的样本容量是 ,样本的平均数是 ,样本的平方和是176时,标准差是 .
20.一组数据2,4,5,1,a的平均数为a,这组数据的方差为 .
三.解答题
21.我市开展了“寻找雷锋足迹”的活动,某中学为了了解七年级800名学生在“学雷锋活动月”中做好事的情况,随机调查了七年级50名学生在一个月内做好事的次数,并将所得数据绘制成统计图,请根据图中提供的信息解答下列问题:
①本次抽样调查的样本容量是 ,样本平均数是 ,众数是 ,极差是 :
②根据样本数据,估计该校七年级800名学生在“学雷锋活动月”中做好事不少于4次的人数.
22.武侯区某学校开展了该校八年级部分学生的综合素质测评活动,随机选取了该校八年级的50名学生进行测评,统计数据如下表:
测评成绩 (单位:分) 80 85 90 95 100
人数 5 10 10 20 5
(1)这50名学生的测评成绩的众数是 分,中位数是 分,极差是 分;
(2)求这50名学生的测评成绩的平均数;
(3)若该校八年级共有学生300名,测评成绩在90分以上(包含90分)为优秀,试估计该校八年级优秀学生共有多少名?
23.某中学开展“唱歌”比赛活动,九年级(1)、(2)班各选出5名选手参加复赛,5名选手的复赛成绩(满分为100分)如图所示:
(1)根据图示填写下表;
班级 中位数(分) 众数(分)
九(1) 85 85
九(2) 80 100
(2)通过计算得知九(2)班的平均成绩为85分,请计算出九(1)班的平均成绩.
(3)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好:
(4)经计算九(1)班复赛成绩的方差为70,请计算九(2)班复赛成绩的方差并说明哪个班学生的成绩比较稳定?
24.在学校组织的科学素养竞赛中,每班参加比赛的人数相同,成绩分为A、B、C、D四个等级,其中相应等级的得分依次为100分,90分,80分,70分.马老师将九年级一班和二班的成绩整理并绘制成如下的统计图:
请你根据以上提供的信息解答下列问题:
(1)此次竞赛中二班成绩在80分及其以上的人数是 人;
(2)求出下表中a、b、c的值;
平均数(分) 中位数(分) 众数(分) 方差
一班 87.6 b 90 106.24
二班 a 80 c 138.24
(3)学校准备在这两个班中选一个班参加市级科学素养竞赛,你建议学校选哪个班参加?说说你的理由.
25.甲、乙两名同学进入八年级后某科6次考试成绩如图所示:
平均数 方差 中位数 众数
甲 75 75
乙 33.3 70
(1)请根据图填写上表;
(2)从平均数和方差结合看,你认为谁的成绩稳定性更好些?
26.某市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了四次测试,测试成绩如表(单位:环):
第一次 第二次 第三次 第四次
甲 9 8 8 7
乙 10 6 7 9
(1)根据表格中的数据,分别计算甲、乙两名运动员的平均成绩;
(2)分别计算甲、乙两人四次测试成绩的方差;根据计算的结果,你认为推荐谁参加省比赛更合适?请说明理由.
27.一次期中考试中,A、B、C、D、E五位同学的数学、语文成绩等有关信息如下表所示:(单位:分)
A B C D E 极差 平均数 标准差
数学 71 72 69 68 70 70
语文 88 82 94 85 76 18 85
其中,表格中的“标准差”是方差的算术平方根.
(1)填写表格中的空档;
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式是:标准分=(个人成绩一平均成绩)÷成绩标准差.从标准分看,标准分大的考试成绩更好.请问A同学在本次考试中,数学与语文哪个学科考得更好?
答案提示
1.A.2.B.3.B.4.C.5.D.6.A.7.B.8.C.9.D.10.D.11.C.12.C.
13.6或﹣3. 14.4. 15.甲. 16.1. 17.2. 18.6,.19. 16,3,. 20.2.
21.解:①根据题意知,样本容量为50;平均数(2×5+3×6+4×13+5×16+6×10)÷50=4.4次;
众数:5次;极差:6﹣2=4次,
故答案为:50、4.4次、5次、4次;
②估计做好事不少于4次的人数:800×=624人.
22.解:(1)这50名学生的测评成绩的众数是95分,中位数是分,极差是100﹣80=20分;
(2)这50名学生的测评成绩的平均数是=91分;
(3)该校八年级优秀学生共有300×=210人,
故答案为:(1)95;92.5;20
23.解:(1)九(1)众数为85分,九(2)班的中位数为80分,
故答案为:80,85;
(2)(分);
(3)从平均数上看,均为85(分),水平相当,
从中位数上看,(1)班85(分)(2)班80分,(1)班好于(2)班,
所以(1)班较好.
(4)=,
∵70<160,
∴(1)班稳定.
24.解:(1)此次竞赛中二班成绩在80分及其以上的人数是:(6+12+2+5)×(1﹣16%)=21(人),
故答案为:21;
(2)由一班竞赛成绩统计图可知,b=90,
二班参加的总人数和一班一样多,二班参加的人数是:6+12+2+5=25,
a=100×44%+90×4%+80×36%+70×16%=87.6,
c=100,
即a=87.6,b=90,c=100;
(3)选择一班参加,
理由:由表格可知,两个班的平均数相同,但一班的中位数高于二班,并且一班的方差小于二班,学生成绩发挥比较稳定,故选择一班.
25.解:(1)乙的平均数:=(85+70+70+75+70+80)=75分,
S=[(60﹣75)2+(65﹣75)2+(75﹣75)2+(75﹣75)2+(80﹣75)2+(95﹣75)2]=125,
乙的中位数为:(70+75)÷2=72.5,甲的众数75,乙的众数为70,
填写表格如下:
平均数 方差 中位数 众数
甲 75 125 75 75
乙 75 33.3 72.5 70
故答案为:75,125,72,5,75;
(2)从平均数上看家、乙两人的成绩相同,但乙的方差较小,说明乙的成绩比较稳定,单从是否稳定上看,乙的成绩较稳定.
26.解:(1)甲的平均成绩是:
(9+8+8+7)÷4=8,
乙的平均成绩是:
(10+6+7+9)÷4=8,
(2)甲的方差是:
[(9﹣8)2+(8﹣8)2+(8﹣8)2+(7﹣8)2]=,
乙的方差是:
[(10﹣8)2+(6﹣8)2+(7﹣8)2+(9﹣8)2]=.
所以推荐甲参加省比赛更合适.理由如下:
两人的平均成绩相等,说明实力相当;
但是甲的四次测试成绩的方差比乙小,说明甲发挥较为稳定,
故推荐甲参加省比赛更合适.
27.解:(1)极差=72﹣68=4,平均分=(71+72+…+70)÷5=70,标准差=6,
故答案为:4;6;
(2)∵数学标准分=,英语标准分=0.5,
∴数学更好.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
