北师大版八年级下册寒假衔接专题讲义第3章 图形的平移与旋转( pdf 无答案)
文档属性
| 名称 | 北师大版八年级下册寒假衔接专题讲义第3章 图形的平移与旋转( pdf 无答案) |  | |
| 格式 | |||
| 文件大小 | 419.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 22:32:35 | ||
图片预览



文档简介
第三章:图形的平移与旋转
第 1 讲:图形的平移与旋转
知识精讲
一.平移与旋转
平移的特征:平移只改变图形的位置,不改变图形的形状与大小
旋转的特征:旋转只改变图形的位置,不改变图形的形状、大小,旋转角都相等
二.角度和线段的计算
1.角度计算:通过旋转角和旋转前后对应角相等并结合题目中给定的特殊条件进行求
解;
2.线段计算:通过旋转前后对应点与旋转中心连线相等的条件构造出等腰三角形,结合
对应边相等和题中特殊条件进行求解.
三.扫过的路径与面积问题
1.路径计算:通过计算旋转角并结合弧长公式得到某一顶点的路径长度;
2.面积计算:通过计算旋转角并结合扇形面积公式得到顶点与其对应点所构成扇形面
积.
四.最值问题
旋转最值的问题一般涉及的是线段长度问题,主要是结合三角形三边关系、两点间直线
段最短、轴对称和圆等知识将所求线段进行转化,一种是转化到一个三角形中,另一种是将
线段转化为可求的直线段或直角三角形中.
五.规律探究
此类问题重点要抓住图形旋转过程中顶点的变化规律,点坐标、线段长度、旋转角等关
键信息的循环规律,再结合平面直角坐标系、勾股定理以及全等的知识去求解.
题模精讲
题模一:角度和线段的计算
例1.1.1如图,△ODC是由△OAB绕点O顺时针旋转31°后得到的图形,若点D恰好落在
AB上,且∠AOC的度数为100°,则∠DOB的度数是( )
第 1 页
A.34° B.36° C.38° D.40°
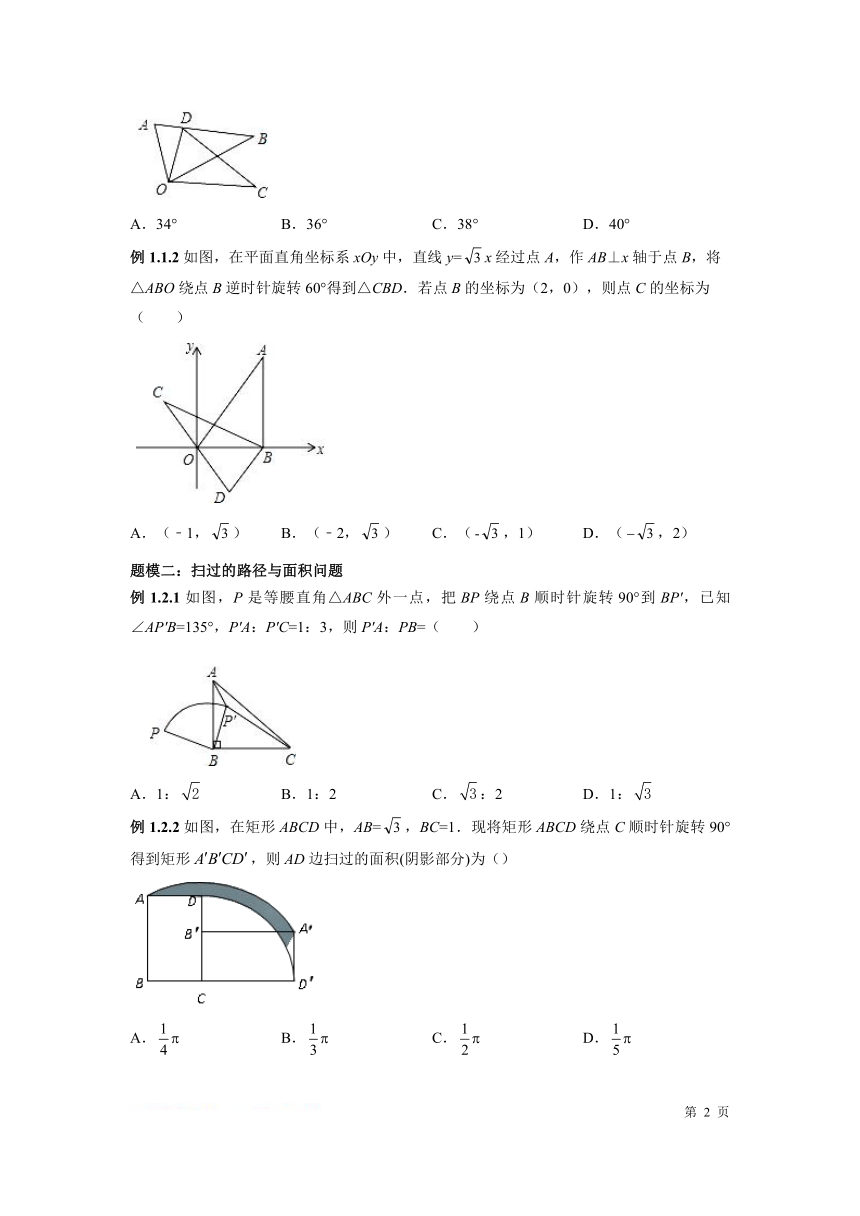
例1.1.2如图,在平面直角坐标系xOy中,直线y= 3x经过点A,作AB⊥x轴于点B,将
△ABO绕点B逆时针旋转60°得到△CBD.若点B的坐标为(2,0),则点C的坐标为
( )
A.(﹣1, 3) B.(﹣2, 3) C.(- 3,1) D.(? 3,2)
题模二:扫过的路径与面积问题
例 1.2.1 如图,P 是等腰直角△ABC 外一点,把 BP 绕点 B 顺时针旋转 90°到 BP′,已知
∠AP′B=135°,P′A:P′C=1:3,则P′A:PB=( )
A.1: 2 B.1:2 C. 3:2 D.1: 3
例1.2.2如图,在矩形ABCD中,AB= 3,BC=1.现将矩形ABCD绕点C顺时针旋转90°
得到矩形A?B?CD?,则AD边扫过的面积(阴影部分)为()
1 1 1 1
A. ? B. ? C. ? D. ?
4 3 2 5
第 2 页
题模三:最值问题
例1.3.1如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足
∠PAB=∠PBC,则线段CP长的最小值为( )
3 8 13 12 13
A. B.2 C. D.
2 13 13
例1.3.2在平面直角坐标系中,点O为坐标原点,A、B、C三点的坐标分别为A(2,0),
B(4,0),C(0,5),点D在第一象限内,且∠ADB=45°.线段CD的长的最小值为 .
题模四:规律探究
例1.4.1观察下列图形,并判断照此规律从左向右第2007个图形是____
A.A选项 B.B选项 C.C选项 D.D选项
例1.4.2如图,在平面直角坐标系xOy中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…
的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4=…=30°.若点A1的坐标为(3,
0),OA1=OC2,OA2=OC3,OA3=OC4…,则依此规律,点A2014的纵坐标为( )
3 3
A.0 B.-3×( )2013
2
第 3 页
2 3
C.(2 3)2014 D.3×( )2013
3
随堂练习
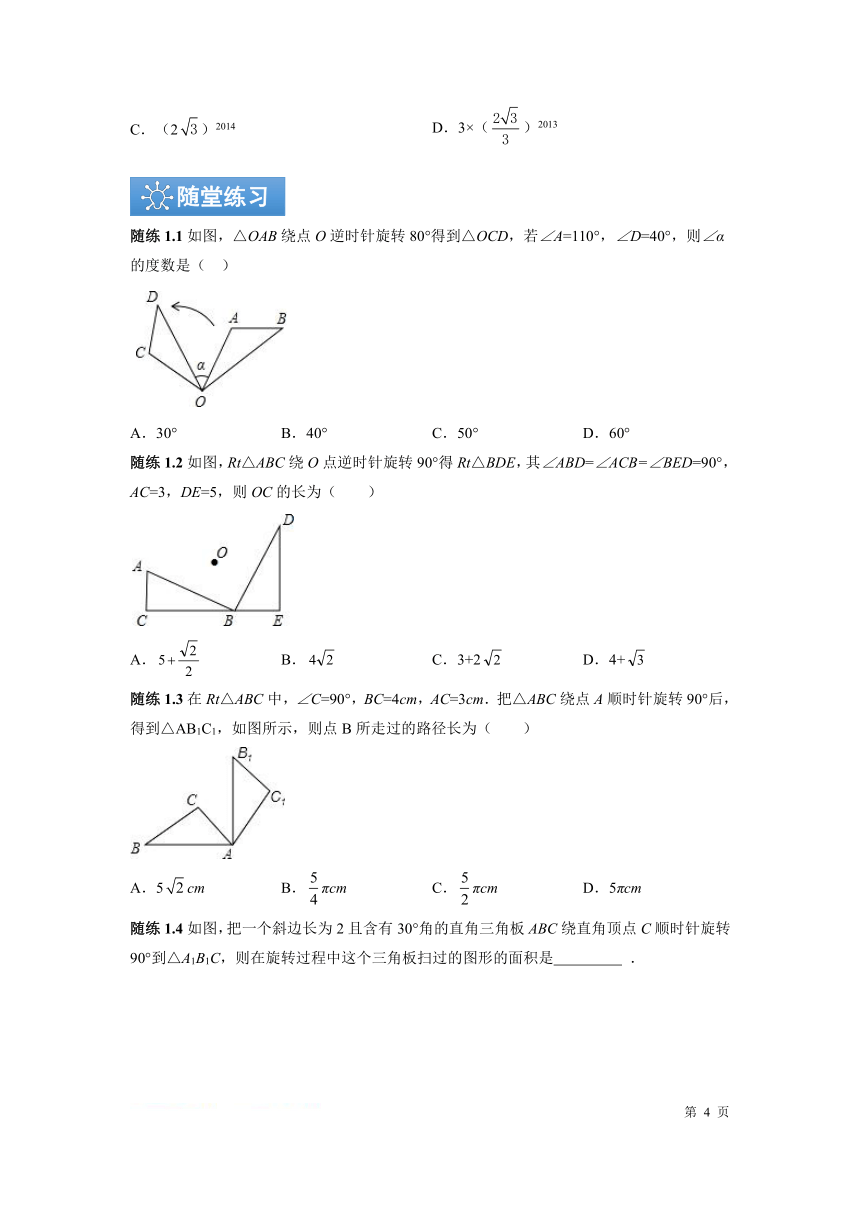
随练1.1如图,△OAB绕点O逆时针旋转80°得到△OCD,若∠A=110°,∠D=40°,则∠α
的度数是( )
A.30° B.40° C.50° D.60°
随练1.2如图,Rt△ABC绕O点逆时针旋转90°得Rt△BDE,其∠ABD=∠ACB=∠BED=90°,
AC=3,DE=5,则OC的长为( )
A. 2
5? B.4 2 C.3+2 2 D.4+ 3
2
随练1.3在Rt△ABC中,∠C=90°,BC=4cm,AC=3cm.把△ABC绕点A顺时针旋转90°后,
得到△AB1C1,如图所示,则点B所走过的路径长为( )
5 5
A.5 2cm B. πcm C. πcm D.5πcm
4 2
随练1.4如图,把一个斜边长为2且含有30°角的直角三角板ABC绕直角顶点C顺时针旋转
90°到△A1B1C,则在旋转过程中这个三角板扫过的图形的面积是 .
第 4 页
随练1.5在Rt△POQ中,OP=OQ=4,M是PQ的中点,把一三角尺的直角顶点放在点M处,
以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.
(1)求证:MA=MB;
(2)连接AB,探究:在旋转三角尺的过程中,△AOB的周长是否存在最小值?若存在,
求出最小值;若不存在,请说明理由.
随练1.6如图Rt△ABC中,∠ACB=90°,∠B=30°,AC=1,且AC在直线l上,将△ABC绕
点A顺时针旋转到①,可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到
位置②,可得到点P2,此时AP2=2+ 3;将位置②的三角形绕点P2顺时针旋转到位置③,
可得到点P3,此时AP3=3+ 3;…按此规律继续旋转,直到点P2012为止,则AP2012等于( )
第 5 页
A.2011?671 3 B.2012?671 3
C.2013?671 3 D.2014?671 3
随练1.7将△ABC放在每个小正方形的边长为1的网格中,点B、C落在格点上,点A在
BC的垂直平分线上,∠ABC=30°,点P为平面内一点.
(1)∠ACB= 度;
(2)如图,将△APC绕点C顺时针旋转60°,画出旋转后的图形(尺规作图,保留痕迹);
(3)AP+BP+CP的最小值为 .
成实外专题
1.(成外)iz已h知:如图1,Rt△ABC中,∠ACB=90? ,D为AB中点,DE、DF分别交AC于E,
交BC于F,且DE⊥DF.
(1)如果CA=CB,求证:AE2+BF2=EF2;
(2)如图2,如果CA说明理由.
第 6 页
2.(实外)变长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,边B1C1
与CD交与点D,则四边形AB1D1D的面积是 .
3.(成外)P为等边△ABC内任意一点,且PA=3,PB=4,PC=5,求∠APB的度数 ___.
4.(自编)如图,AB两村之间有两条平行的河,一河宽a;另一个宽为b现欲在两条河上各
造一座桥(桥必须与河岸垂直),使得A、B之间的路程最短,试找出造桥位置.
5.(培优)如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴
上,连接AC,将矩形纸片OABC沿AC折叠,使点B落在点D的位置,若B(1,2),则点D的横坐标
是 .
3
6. (培优)如图,在平面直角坐标系中,已知直线 y ?? x?3与x轴、y轴分别交于A、B
4
两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,使点B刚好落在x轴上B'处,则点C
的坐标是 .
第 7 页
7. (培优) 如图,在矩形纸片ABCD中,AB=5cm,BC=10cm,CD上有一点E,ED=2cm,
AD上有一点P,PD=3cm,过P作PF⊥AD交BC于F,将纸片折叠,使P点与E点重合,
折痕与PF交于Q点,则PQ的长是 cm.
8.(培优)在三角形纸片ABC中,已知∠ABC=90°,AB=6,BC=8.过点A作直线l平行于
BC,折叠三角形纸片ABC,使直角顶点B落在直线l上的T处,折痕为MN.当点T在直
线l上移动时,折痕的端点M、N也随之移动.若限定端点M、N分别在AB、BC边上移动,
则线段AT长度的最大值与最小值之和为________(计算结果不取近似值)
课后作业
作业1如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△AB′C′的位置,使
得CC′∥AB,则∠BAB′的度数是( )
A.70° B.35° C.40° D.50°
第 8 页
作业2如图,在△ABC中,∠C=90°,AC=BC= 2 ,将△ABC绕点 A顺时针方向旋转
60°到△AB′C′的位置,连接 C′B,则 C′B= .
作业3如图,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2.将△ABC绕直角顶点C逆时
针旋转60°得△A′B′C,则点B转过的路径长为( )
?
A. B. 3 2
? C. ? D.π
3 3 3
作业4如图,在矩形ABCD中,AB=3,AD=4,将矩形ABCD绕点D顺时针旋转90°得到矩
形A′B′C′D′,则点B经过的路径与BA,AC′,C′B′所围成封闭图形的面积是____________(结
果保留π).
作业5如图,在直角坐标系中,已知点A(-3,0)、B(0,4),对△OAB连续作旋转变换,
依次得到△1、△2、△3、△4…,则△2013的直角顶点的坐标为____.
作业6(2015.重庆)在△ABC中,AB=AC,∠A=60°,点D是线段BC的中点,∠EDF=120°,
第 9 页
DE与线段AB相交于点E,DF与线段AC(或AC的延长线)相交于点F.
(1)如图1,若DF⊥AC,垂足为F,AB=4,求BE的长;
(2)如图2,将(1)中的∠EDF绕点D顺时针旋转一定的角度,DF仍与线段AC相交于
点F.求证: 1
BE+CF= AB
2
(3)如图3,将(2)中的∠EDF继续绕点D顺时针旋转一定的角度,使DF与线段AC的
延长线交与点F,作DN⊥AC于点N,若DN=FN,求证:BE+CF= 3(BE-CF)
第 10 页
第 1 讲:图形的平移与旋转
知识精讲
一.平移与旋转
平移的特征:平移只改变图形的位置,不改变图形的形状与大小
旋转的特征:旋转只改变图形的位置,不改变图形的形状、大小,旋转角都相等
二.角度和线段的计算
1.角度计算:通过旋转角和旋转前后对应角相等并结合题目中给定的特殊条件进行求
解;
2.线段计算:通过旋转前后对应点与旋转中心连线相等的条件构造出等腰三角形,结合
对应边相等和题中特殊条件进行求解.
三.扫过的路径与面积问题
1.路径计算:通过计算旋转角并结合弧长公式得到某一顶点的路径长度;
2.面积计算:通过计算旋转角并结合扇形面积公式得到顶点与其对应点所构成扇形面
积.
四.最值问题
旋转最值的问题一般涉及的是线段长度问题,主要是结合三角形三边关系、两点间直线
段最短、轴对称和圆等知识将所求线段进行转化,一种是转化到一个三角形中,另一种是将
线段转化为可求的直线段或直角三角形中.
五.规律探究
此类问题重点要抓住图形旋转过程中顶点的变化规律,点坐标、线段长度、旋转角等关
键信息的循环规律,再结合平面直角坐标系、勾股定理以及全等的知识去求解.
题模精讲
题模一:角度和线段的计算
例1.1.1如图,△ODC是由△OAB绕点O顺时针旋转31°后得到的图形,若点D恰好落在
AB上,且∠AOC的度数为100°,则∠DOB的度数是( )
第 1 页
A.34° B.36° C.38° D.40°
例1.1.2如图,在平面直角坐标系xOy中,直线y= 3x经过点A,作AB⊥x轴于点B,将
△ABO绕点B逆时针旋转60°得到△CBD.若点B的坐标为(2,0),则点C的坐标为
( )
A.(﹣1, 3) B.(﹣2, 3) C.(- 3,1) D.(? 3,2)
题模二:扫过的路径与面积问题
例 1.2.1 如图,P 是等腰直角△ABC 外一点,把 BP 绕点 B 顺时针旋转 90°到 BP′,已知
∠AP′B=135°,P′A:P′C=1:3,则P′A:PB=( )
A.1: 2 B.1:2 C. 3:2 D.1: 3
例1.2.2如图,在矩形ABCD中,AB= 3,BC=1.现将矩形ABCD绕点C顺时针旋转90°
得到矩形A?B?CD?,则AD边扫过的面积(阴影部分)为()
1 1 1 1
A. ? B. ? C. ? D. ?
4 3 2 5
第 2 页
题模三:最值问题
例1.3.1如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足
∠PAB=∠PBC,则线段CP长的最小值为( )
3 8 13 12 13
A. B.2 C. D.
2 13 13
例1.3.2在平面直角坐标系中,点O为坐标原点,A、B、C三点的坐标分别为A(2,0),
B(4,0),C(0,5),点D在第一象限内,且∠ADB=45°.线段CD的长的最小值为 .
题模四:规律探究
例1.4.1观察下列图形,并判断照此规律从左向右第2007个图形是____
A.A选项 B.B选项 C.C选项 D.D选项
例1.4.2如图,在平面直角坐标系xOy中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…
的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4=…=30°.若点A1的坐标为(3,
0),OA1=OC2,OA2=OC3,OA3=OC4…,则依此规律,点A2014的纵坐标为( )
3 3
A.0 B.-3×( )2013
2
第 3 页
2 3
C.(2 3)2014 D.3×( )2013
3
随堂练习
随练1.1如图,△OAB绕点O逆时针旋转80°得到△OCD,若∠A=110°,∠D=40°,则∠α
的度数是( )
A.30° B.40° C.50° D.60°
随练1.2如图,Rt△ABC绕O点逆时针旋转90°得Rt△BDE,其∠ABD=∠ACB=∠BED=90°,
AC=3,DE=5,则OC的长为( )
A. 2
5? B.4 2 C.3+2 2 D.4+ 3
2
随练1.3在Rt△ABC中,∠C=90°,BC=4cm,AC=3cm.把△ABC绕点A顺时针旋转90°后,
得到△AB1C1,如图所示,则点B所走过的路径长为( )
5 5
A.5 2cm B. πcm C. πcm D.5πcm
4 2
随练1.4如图,把一个斜边长为2且含有30°角的直角三角板ABC绕直角顶点C顺时针旋转
90°到△A1B1C,则在旋转过程中这个三角板扫过的图形的面积是 .
第 4 页
随练1.5在Rt△POQ中,OP=OQ=4,M是PQ的中点,把一三角尺的直角顶点放在点M处,
以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.
(1)求证:MA=MB;
(2)连接AB,探究:在旋转三角尺的过程中,△AOB的周长是否存在最小值?若存在,
求出最小值;若不存在,请说明理由.
随练1.6如图Rt△ABC中,∠ACB=90°,∠B=30°,AC=1,且AC在直线l上,将△ABC绕
点A顺时针旋转到①,可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到
位置②,可得到点P2,此时AP2=2+ 3;将位置②的三角形绕点P2顺时针旋转到位置③,
可得到点P3,此时AP3=3+ 3;…按此规律继续旋转,直到点P2012为止,则AP2012等于( )
第 5 页
A.2011?671 3 B.2012?671 3
C.2013?671 3 D.2014?671 3
随练1.7将△ABC放在每个小正方形的边长为1的网格中,点B、C落在格点上,点A在
BC的垂直平分线上,∠ABC=30°,点P为平面内一点.
(1)∠ACB= 度;
(2)如图,将△APC绕点C顺时针旋转60°,画出旋转后的图形(尺规作图,保留痕迹);
(3)AP+BP+CP的最小值为 .
成实外专题
1.(成外)iz已h知:如图1,Rt△ABC中,∠ACB=90? ,D为AB中点,DE、DF分别交AC于E,
交BC于F,且DE⊥DF.
(1)如果CA=CB,求证:AE2+BF2=EF2;
(2)如图2,如果CA
第 6 页
2.(实外)变长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,边B1C1
与CD交与点D,则四边形AB1D1D的面积是 .
3.(成外)P为等边△ABC内任意一点,且PA=3,PB=4,PC=5,求∠APB的度数 ___.
4.(自编)如图,AB两村之间有两条平行的河,一河宽a;另一个宽为b现欲在两条河上各
造一座桥(桥必须与河岸垂直),使得A、B之间的路程最短,试找出造桥位置.
5.(培优)如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴
上,连接AC,将矩形纸片OABC沿AC折叠,使点B落在点D的位置,若B(1,2),则点D的横坐标
是 .
3
6. (培优)如图,在平面直角坐标系中,已知直线 y ?? x?3与x轴、y轴分别交于A、B
4
两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,使点B刚好落在x轴上B'处,则点C
的坐标是 .
第 7 页
7. (培优) 如图,在矩形纸片ABCD中,AB=5cm,BC=10cm,CD上有一点E,ED=2cm,
AD上有一点P,PD=3cm,过P作PF⊥AD交BC于F,将纸片折叠,使P点与E点重合,
折痕与PF交于Q点,则PQ的长是 cm.
8.(培优)在三角形纸片ABC中,已知∠ABC=90°,AB=6,BC=8.过点A作直线l平行于
BC,折叠三角形纸片ABC,使直角顶点B落在直线l上的T处,折痕为MN.当点T在直
线l上移动时,折痕的端点M、N也随之移动.若限定端点M、N分别在AB、BC边上移动,
则线段AT长度的最大值与最小值之和为________(计算结果不取近似值)
课后作业
作业1如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△AB′C′的位置,使
得CC′∥AB,则∠BAB′的度数是( )
A.70° B.35° C.40° D.50°
第 8 页
作业2如图,在△ABC中,∠C=90°,AC=BC= 2 ,将△ABC绕点 A顺时针方向旋转
60°到△AB′C′的位置,连接 C′B,则 C′B= .
作业3如图,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2.将△ABC绕直角顶点C逆时
针旋转60°得△A′B′C,则点B转过的路径长为( )
?
A. B. 3 2
? C. ? D.π
3 3 3
作业4如图,在矩形ABCD中,AB=3,AD=4,将矩形ABCD绕点D顺时针旋转90°得到矩
形A′B′C′D′,则点B经过的路径与BA,AC′,C′B′所围成封闭图形的面积是____________(结
果保留π).
作业5如图,在直角坐标系中,已知点A(-3,0)、B(0,4),对△OAB连续作旋转变换,
依次得到△1、△2、△3、△4…,则△2013的直角顶点的坐标为____.
作业6(2015.重庆)在△ABC中,AB=AC,∠A=60°,点D是线段BC的中点,∠EDF=120°,
第 9 页
DE与线段AB相交于点E,DF与线段AC(或AC的延长线)相交于点F.
(1)如图1,若DF⊥AC,垂足为F,AB=4,求BE的长;
(2)如图2,将(1)中的∠EDF绕点D顺时针旋转一定的角度,DF仍与线段AC相交于
点F.求证: 1
BE+CF= AB
2
(3)如图3,将(2)中的∠EDF继续绕点D顺时针旋转一定的角度,使DF与线段AC的
延长线交与点F,作DN⊥AC于点N,若DN=FN,求证:BE+CF= 3(BE-CF)
第 10 页
同课章节目录
