多边形的内角和习题(无答案)
图片预览
文档简介
第一讲 多边形的内(外)角和
试求8边形、19边形、199边形的内角和。
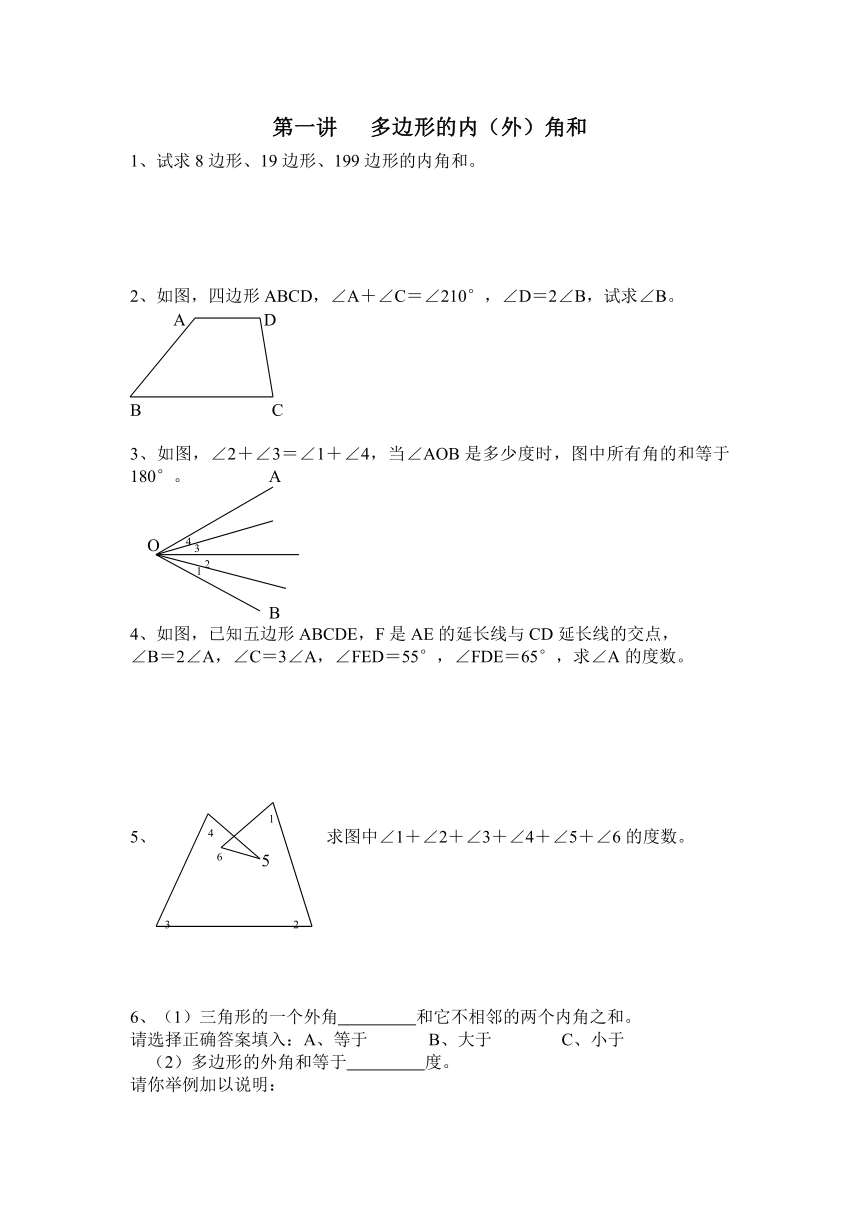
如图,四边形ABCD,∠A+∠C=∠210°,∠D=2∠B,试求∠B。
A D
B C
3、如图,∠2+∠3=∠1+∠4,当∠AOB是多少度时,图中所有角的和等于180°。 A
O 4 3
1 2
B
4、如图,已知五边形ABCDE,F是AE的延长线与CD延长线的交点,
∠B=2∠A,∠C=3∠A,∠FED=55°,∠FDE=65°,求∠A的度数。
1
5、 4 求图中∠1+∠2+∠3+∠4+∠5+∠6的度数。
6 5
3 2
6、(1)三角形的一个外角 和它不相邻的两个内角之和。
请选择正确答案填入:A、等于 B、大于 C、小于
(2)多边形的外角和等于 度。
请你举例加以说明:
7、 3 如图,求∠1,∠2,∠3分别是多少度?
70°
1 40°2
8、图形里的学问
8-1 8-2 8-3
图8-1看上去很简单,你若从不同的角度去观察,学问就大哪!
图8-2中用粗线隔开,隔开后的小方格的个数分别是:1、3、5、9…根据正方形中小方格的计算方法,把数和形结合起来思考就可以得到:
1=12
1+3=22
1+3+5=32
1+3+5+7=42
……
你概括出一个结论:
根据这个结论,你一定能很快求出下列各式的值。
1+3+5+7+……+19=( )2=( )
51+53+55+………+199=( )2-( )2=( )
若像图8-3那样划分,你又能得到什么规律呢?
试求8边形、19边形、199边形的内角和。
如图,四边形ABCD,∠A+∠C=∠210°,∠D=2∠B,试求∠B。
A D
B C
3、如图,∠2+∠3=∠1+∠4,当∠AOB是多少度时,图中所有角的和等于180°。 A
O 4 3
1 2
B
4、如图,已知五边形ABCDE,F是AE的延长线与CD延长线的交点,
∠B=2∠A,∠C=3∠A,∠FED=55°,∠FDE=65°,求∠A的度数。
1
5、 4 求图中∠1+∠2+∠3+∠4+∠5+∠6的度数。
6 5
3 2
6、(1)三角形的一个外角 和它不相邻的两个内角之和。
请选择正确答案填入:A、等于 B、大于 C、小于
(2)多边形的外角和等于 度。
请你举例加以说明:
7、 3 如图,求∠1,∠2,∠3分别是多少度?
70°
1 40°2
8、图形里的学问
8-1 8-2 8-3
图8-1看上去很简单,你若从不同的角度去观察,学问就大哪!
图8-2中用粗线隔开,隔开后的小方格的个数分别是:1、3、5、9…根据正方形中小方格的计算方法,把数和形结合起来思考就可以得到:
1=12
1+3=22
1+3+5=32
1+3+5+7=42
……
你概括出一个结论:
根据这个结论,你一定能很快求出下列各式的值。
1+3+5+7+……+19=( )2=( )
51+53+55+………+199=( )2-( )2=( )
若像图8-3那样划分,你又能得到什么规律呢?
