北师大版七年级上册第三章整式及其加减总复习(学案)
文档属性
| 名称 | 北师大版七年级上册第三章整式及其加减总复习(学案) | 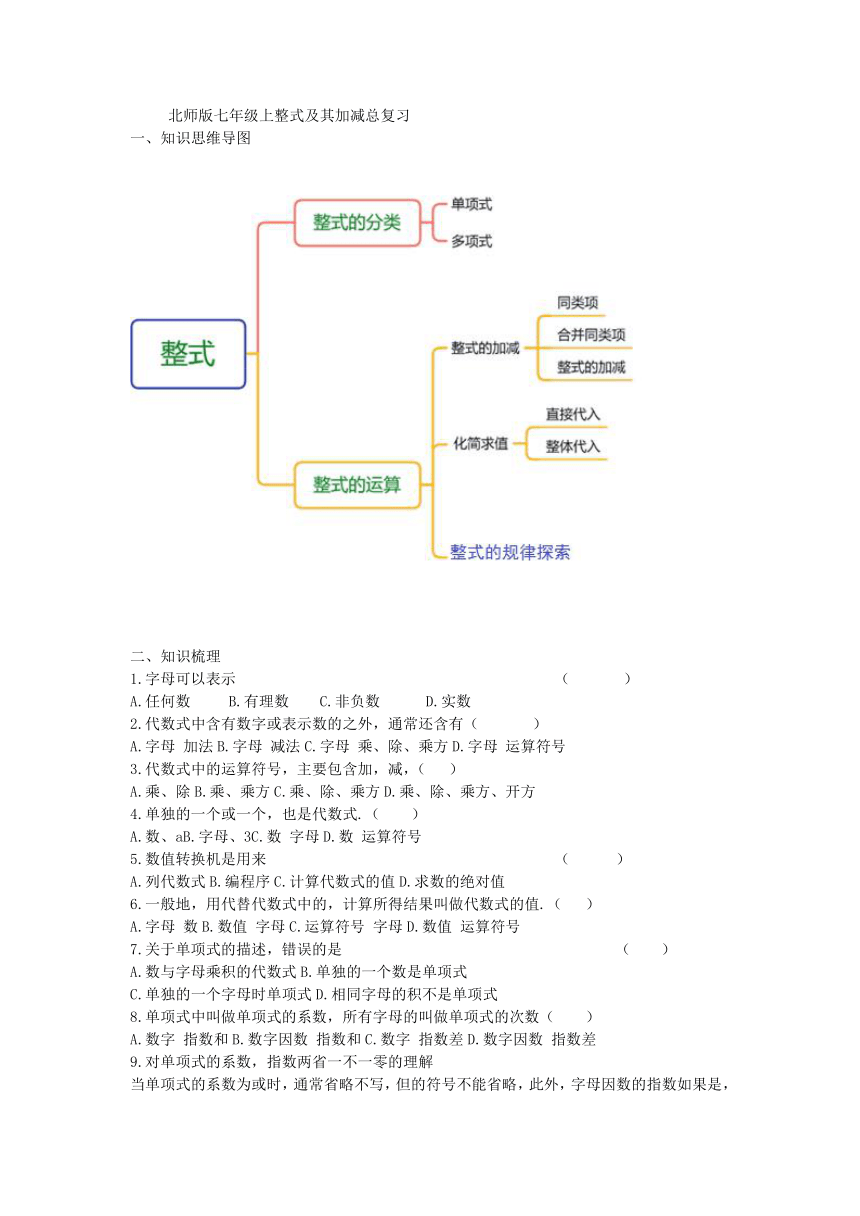 | |
| 格式 | zip | ||
| 文件大小 | 456.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 23:14:08 | ||
图片预览





文档简介
北师版七年级上整式及其加减总复习
知识思维导图
二、知识梳理
1.字母可以表示
(
)
A.任何数
B.有理数
C.非负数
D.实数
2.代数式中含有数字或表示数的之外,通常还含有(
)
A.字母
加法B.字母
减法C.字母
乘、除、乘方D.字母
运算符号
3.代数式中的运算符号,主要包含加,减,(
)
A.乘、除B.乘、乘方C.乘、除、乘方D.乘、除、乘方、开方
4.单独的一个或一个,也是代数式.(
)
A.数、aB.字母、3C.数
字母D.数
运算符号
5.数值转换机是用来
(
)
A.列代数式B.编程序C.计算代数式的值D.求数的绝对值
6.一般地,用代替代数式中的,计算所得结果叫做代数式的值.(
)
A.字母
数B.数值
字母C.运算符号
字母D.数值
运算符号
7.关于单项式的描述,错误的是
(
)
A.数与字母乘积的代数式B.单独的一个数是单项式
C.单独的一个字母时单项式D.相同字母的积不是单项式
8.单项式中叫做单项式的系数,所有字母的叫做单项式的次数(
)
A.数字
指数和B.数字因数
指数和C.数字
指数差D.数字因数
指数差
9.对单项式的系数,指数两省一不一零的理解
当单项式的系数为或时,通常省略不写,但的符号不能省略,此外,字母因数的指数如果是,通常也省略不写;单独的一个非零数的次数是.
10.几个单项式的叫做多项式.(
)
A.和B.差C.积D.商
11.在多项式中,每个叫做多项式的项,不含的项叫做常数项.(
)
A.代数式
字母B.单项式
字母C.字母
字母D.单项式
单项式
12.和统称整式.
(
)
A.单项式
代数式B.多项式
代数式C.单项式多项式D.代数式
代数式
13.所含相同,并且的指数也的项叫做同类项.(
)
A.字母
相同字母
相同B.字母
相同字母不相同
C.字母
不同字母
相同
D.字母
不同字母不相同
14.下列说法,正确的是
(
)
A.所有字母都是同类项B.所有多项式都是同类项
C.所有常数项都是同类项D.所有单项式都是同类项
15.把合并成一项,叫做合并同类项.
(
)
A.单项式B.多项式C.整式D.同类项
16.合并同类项的依据是
(
)
A.乘法对加法的结合律B.乘法对加法的分配律C.加法的交换律D.加法的结合律
17.合并同类项时,把同类项的相加,字母和字母的不变.(
)
A.项
次数B.系数
指数C.指数
指数D.系数,系数
18.括号前是“+”号,把和它前面的“+”号去掉后,原来括号里各项的符号都(
)
A.括号
改变B.括号
不改变C.系数
改变D.指数
不改变
19.括号前是“-”号,把和它前面的“-”号去掉后,原来括号里各项的符号都(
)
A.括号
改变
B.括号
不改变C.系数
改变
D.指数
不改变
20.进行整式加减运算时,如果遇到括号,要先,再
(
)
A.去掉括号
把指数相加B.去掉括号
把系数相加
C.去掉括号
合并同类项D.去掉括号
合并单项式
三、知识应用
考点
1:布列代数式
例1(2020长沙).某数学老师在课外活动中做了一个有趣的游戏:首先发给A,B,C三个同学相同数量的扑克牌(假定发到每个同学手中的扑克牌数量足够多),然后依次完成下列三个步骤:
第一步,A同学拿出三张扑克牌给B同学;
第二步,C同学拿出三张扑克牌给B同学;
第三步,A同学手中此时有多少张扑克牌,B同学就拿出多少张扑克牌给A同学,
请你确定,最终B同学手中剩余的扑克牌的张数为___________________.
题意剖析:
以扑克游戏为问题背景,让学生感到亲切,不反感,反映了数学源于生活的思想,同时,为了解决问题,需要用到字母表示数的思想,学会熟练规范进行代数式的布列,巩固了相应的数学知识,落实了让学生在玩中学的课标学习目标,值得点赞!
解法直播:
解法1:设每个同学扑克牌的数量都是;
第一步,A同学的扑克牌的数量是,B同学的扑克牌的数量是;
第二步,B同学的扑克牌的数量是,C同学的扑克牌的数量是;
第三步,A同学的扑克牌的数量是2(),B同学的扑克牌的数量是();
∴B同学手中剩余的扑克牌的数量是:().故答案为:.
点评:按照题目的操作顺序,步步为营,紧紧指向目标,是常用的求解思路.
解法2:设每个同学扑克牌的数量都是,列表如下:
所以答案为9.
点评:列表法是数学解题的一种非常实用有效的解题方法,最大特点是简洁,直观,易懂易操作,是值得同学们熟练掌握的好解题方法.
考点2:求代数式的值
(1)整体代入
例2(2020重庆B卷)已知a+b=4,则代数式1+的值为
(
)
A.3
B.1
C.0
D.-1
解析:因为=,a+b=4,所以原式=1+=3,所以选A.
点评:把握已知条件,梳理所求代数式的特点,选择整体代入求值是正确的选择.
(2)单一代入
例3(2020年黄岗)若|x-2|+=0,则-xy=
.
解:,,,,,
,故答案为:2.
点评:活用实数的非负性质,求得每个字母的值,为代数式的值计算提供支撑.
考点3:单项式
活动1:确定单项式的系数
例4(2019湖南怀化)单项式﹣5ab的系数是
( )
5
B.﹣5
C.2
D.﹣2
分析:单项式的一般结构是数字因数+字母因数,其中的数字因数叫做单项式的系数,注意系数一定要包含数的符号.特别地,单纯的数不能称系数,单独的字母其系数为1或-1,通常数字“1”省略不写,只写其符号代替.
解:-5ab的数字因数为-5,所以单项式-5ab的系数为-5,所以选B.
活动2:确定单项式的次数
例5(2019,山东淄博)单项式的次数是
.
分析:单项式的次数是所有字母指数的和,就现阶段的内容看,单项式的次数一定是正整数.
谨记字母的指数最小是1,如a的指数是1,绝对不是0,否则计算的结果一定是错误的.
解:因为a的次数是3,b的次数为2,所以单项式的次数为3+2=5,所以填5.
活动3:探索单项式中的变化规律
例6(2019?云南)按一定规律排列的单项式:,-,,-,,……第n个单项式是
(
)
A.
B.
C.
D.
分析:观察各单项式,发现奇数项系数为正,偶数项系数为负,所以可以用或(为大于等于1的整数)来控制系数的正负,指数为从3开始的奇数,所以指数部分规律为2n+1.整体处理即可得到答案.
解:观察可知,奇数项系数为正,偶数项系数为负,所以可以用或
(为大于等于1的整数)来控制系数的正负,指数为从3开始的奇数,所以指数部分规律为2n+1,所以选C.
活动4:阅读创新,提高自学能力
例7(2019湖南张家界)阅读下面的材料:
按照一定顺序排列着的一列数称为数列,数列中的每一个数叫做这个数列的项.排在第一位的数称为第一项,记为,排在第二位的数称为第二项,记为,依此类推,排在第n位的数称为第n项,记为.所以,数列的一般形式可以写成:,,,…,,….
一般地,如果一个数列从第二项起,每一项与它前一项的差等于同一个常数,那么这个数列叫做等差数列,这个常数叫做等差数列的公差,公差通常用d表示.如:数列1,3,5,7,…为等差数列,其中=1,=3,公差为d=2.根据以上材料,解答下列问题:
(1)等差数列5,10,15,…的公差d为 ,第5项是 .
(2)如果一个数列,,,…,,…,是等差数列,且公差为d,那么根据定义可得到-=d,﹣=d,-=d,…,-=d,….所以=+d,
=+d=(+d)+d=+2d,=+d=(+2d)+d=+3d,……
由此,请你填空完成等差数列的通项公式:=+( )d.
(3)﹣4041是不是等差数列﹣5,﹣7,﹣9…的项?如果是,是第几项?
分析:这是一道高中基础知识下移生成的阅读型考题,其意义有五:一是培养学生的阅读能力,这是解题的基础,题意都读不懂,更难说解题;二是培养学生的自学能力,学会理解题意,学会寻找解题方法;三是培养自我接受新鲜事物的能力,特别是接受新知识的能力,这是全面数学素养提升的基础;四是培养寻找系数与序号之间的变化规律的探索能力;培养学生学以致用的问题解决能力.
解:(1)根据题意得,d=10﹣5=5;因为=15,所以=+d=15+5=20,所以=+d=20+5=25,
所以应该填5;25.
(2)因为=+(2-1)d,=+d=(+d)+d=+2d=+(3-1)d,
=+d=(+2d)+d=+3d=+(4-1)d,……所以=+(n﹣1)d,所以应该填
n﹣1.
(3)因为等差数列﹣5,﹣7,﹣9…中,=-5,d=-7-(-5)=﹣2,所以=+(n﹣1)d=-5-2(n-1),因为﹣5﹣2(n﹣1)=﹣4041,解得:n=2019,符合题意,所以﹣4041是等差数列﹣5,﹣7,﹣9…的项,且它是此数列的第2019项.
考点4
同类型型
例8(2020贵州黔西南)若7与﹣的和为单项式,则=
.
解析:因为7与﹣的和为单项式,所以7与﹣是同类型,
所以x=3,y=2,所以==8.
点评:这是单项式与同类型两个基本概念之间的内在联系,抓住联系,将概念题目化,不仅考查了对单个概念的理解与应用,更注重了概念间的联系,实现了培养数学综合能力的解题的目标.
例9(2020苏州)若单项式与单项式是同类项,则________.
解析:因为单项式与单项式是同类项,所以m-1=2,n+1=2,
所以m=3,n=1,所以m+n=3+1=4;(2)所以m-1+n+1=2+2,所以m+n=4.
点评:同类项型概念题是中考的常考题型,也是基础性考题之一,解答时,注意如下几点:1.落实好两个对应即明确对应字母,后根据对应字母的指数对应相等构造出解题需要的等式;2.根据等式,完成对字母值的确定;3.化归为代数式的值问题求解思路,确定最终的结果.解答时,要注意用好两种求解思路:单字母值确定法,这是解题的同法,也是同学们最常用的方法;整体求值法,根据条件的特点,可将两个等式求和或求差,得到答案.
考点5多项式型
例10(2020年绵阳)若多项式x+(n-2)+1是关于x,y的三次多项式,则mn=.
解析:因为多项式x+(n-2)+1是关于x,y的三次多项式,所以n-2=0,
且|m-n|=2,所以n=2,|m-2|=2,所以m=4,n=2,或m=0,n=2,所以mn=8或mn=0.
点评:抓住多项式的次数定义是完成解题的根本依据,解答时,注意如下几点:
1.多项式的次数是多项式中每一个单项式次数的最高次数,具备最高次数的单项式可以不唯一;
2.熟记单项式次数的确定方法,各字母指数的和,为解题构造等式提供支撑;
3.掌握消除高于最高次数的项的基本方法:令该项的系数为0,0与任何数,任何式的积均为0,从而实现消项的目标.
考点6编程计算
1.以“0”为参照标准的单一代数式的编程计算
例11(2020江苏连云港)按照如图1所示的计算程序,若x=2,则输出的结果是
.
分析:编程计算,简洁但内涵丰富,解答时,需要准确理解编程计算的意义和计算原理,其基本结构为:输入值→代数式→转化为代数式的值→对照标准→符合→输出,不符合,代数式的值作为新输入值,进行再次流程计算,直到符合标准为止.
解析:
当x=2时,10-=10-=6>0,不符合标准,当x=6时,10-=10-=10-36=-26<0,符合标准,可以输出,所以输出的结果是-26.
点评:编程计算的实质是求代数式的值,是一种符合标准输出,不符合标准,代数式的值转化为输入值重新计算值的重复型计算题,理解编程计算的实质和意义是解题的关键.
2.分类输入两代数式的规律探索型编程计算
例12(2020贵州黔西南)如图2,是一个运算程序的示意图,若开始输入x的值为625,则
第2020次输出的结果为
.
分析:程序的基本特点,对输入数按照等于1和不等于1进行分类,后进行分类计算,通过反复的输入计算,寻找其中的基本规律,利用循环节的思想方法求解即可.
解析:当x=625时≠1,所以x=125;当x=125时≠1,所以x=25;
当x=25时≠1,所以x=5;当x=5时≠1,所以x=1;
当x=1时,x+4=5,当x=5时≠1,所以x=1;…依此类推,以5,1值进行循环,循环节为2,因为(2020﹣2)÷2=1010,所以第2020次的结果为1即输出的结果是1.
点评:解答时,不要急躁,通过进行多步计算,将问题转化为循环节问题,这是解题的关键.确定从第几步开始,循环节是多少,循环值的对应变化规律都是解题时必须要解决的问题,要熟练掌握.
考点7
规律探索
1.黑色三角形拼图摆放中寻找规律
例13(2020重庆A卷)把黑色三角形按如图所示的规律拼图案,其中第①个图案中有1个黑色三角形,第②个图案中有3个黑色三角形,第③个图案中有6个黑色三角形,…,按此规律排列下去,则第⑤个图案中黑色三角形的个数为
(
)
A.
10
B.
15
C.
18
D.
21
解析:∵第①个图案中黑色三角形的个数为1,第②个图案中黑色三角形的个数3=1+2,
第③个图案中黑色三角形的个数6=1+2+3,……,∴第⑤个图案中黑色三角形的个数为1+2+3+4+5=15,故选:B.
点评:选择正确的试题角度是解题的关键.从上而下,分层数,分别加,是解题的根本.
其一般性规律为:第n个图案中,黑三角形的个数:1+2+3+……+n=.
其计算思想恰好是高斯计算思想的再现,在寻找规律中,缅怀了数学名人.
2.正三角形拼图摆放中寻找规律
例14(2020山西)(3分)如图是一组有规律的图案,它们是由边长相等的正三角形组合而成,第1个图案有4个三角形,第2个图案有7个三角形,第3个图案有10个三角形…按此规律摆下去,第n个图案有
个三角形(用含n的代数式表示).
解法1:整体元分割法,列表思索如下:
所以第n个图案有(3n+1)个三角形.故答案为:(3n+1).
点评:此法采用图形整体元分解法,准确实施图形分割是解题的关键.这里也体现局部整体思维的智慧,实现了整体变化,局部稳定的解题探索.
解法2:上、下二层分割法
第一个图案数:2+1+1=4;第二个图案数:2×2+2+1=7;第三个图案数:3×2+3+1=10;
第四个图案数:4×2+4+1=13;…,第n个图案数:n×2+n+1=3n+1,.故答案为:(3n+1).
点评:合理分层使得规律发现更容易,更容易总结,这也体现了数学创新精神的课标要求,培养自我数学创新意识.
3.实心圆点摆放中寻找规律
例15(2020重庆B卷)下列图形都是由同样大小的实心圆点按一定规律组成的,其中第①个图形一共有5个实心圆点,第②个图形一共有8个实心圆点,第③个图形一共有11个实心圆点,?,按此规律排列下去,第⑥个图形中实心圆点的个数为
(
)
A.18
B.
19
C.20
D.21
解析:横、纵二层分割法探索列表如下:
所以第n个图案中,圆点数为(3n+2)个,当n=6时,3n+2=20,所以选C.
点评:科学分割图案,用序号分别表示横,纵圆点数是解题的关键.
4.菱形摆放中寻找规律
例16(2020贵州黔西南)如图图形都是由同样大小的菱形按照一定规律所组成的,其中第①
个图形中一共有3个菱形,第②个图形中一共有7个菱形,第③个图形中一共有13个菱形,…,
按此规律排列下去,第⑦个图形中菱形的个数为
.
解析:继续采用二层分割法
第①个图形中上层1,下层1+1,即1+1+1=3,一共有3个菱形;
第②个图形中上层1+2+1,下层2+1,即+2+1=7,一共有7个菱形;
第③个图形中上层1+2+3+2+1下层3+1,即+3+1=13,一共有33个菱形;
…,按此规律排列下去,
第n个图形中上层1+2+…+n+…+2+1,下层n+1,即+n+1,一共有(+n+1)个菱形;
所以第⑦个图形中菱形的个数为:+n+1=+7+1=57.所以答案为:57.
点评:上下二层分割法是解题的方法引领,代数式变形为序号为底数的自然数完全平方,是解题的关键,灵活变形是解题的创新灵魂所在.
例17(2020海南)海南黎锦有着悠久的历史,已被列入世界非物质文化遗产名录.如图是黎锦上的图案,每个图案都是由相同菱形构成的,若按照第1个图至第4个图中的规律编织图案,则第5个图中有 个菱形,第n个图中有
个菱形(用含n的代数式表示).
解析:∵第1个图中菱形的个数1=+;第2个图中菱形的个数5=+;
第3个图中菱形的个数13=+;第4个图中菱形的个数25=+
∴第5个图中菱形的个数为+=41,
第n个图中菱形的个数为+=2-2n+1,故答案为:41,2-2n+1.
点评:这个图示,实际上是勾股数的变式,这启示同学们,在常态学习时,不仅要注意式子的学习,更要掌握式子的形的意义,这样才能全面掌握,全面学习,继而实现数形结合的思想的提炼与渗透,实现培养数学核心素养的数学学习目标.
5.恒等式中寻找规律
例18(2020青海)(4分)观察下列各式的规律:
①1×3﹣22=3﹣4=﹣1;②2×4﹣32=8﹣9=﹣1;③3×5﹣42=15﹣16=﹣1.
请按以上规律写出第4个算式
.
用含有字母的式子表示第n个算式为
.
解析:④4×6﹣52=24﹣25=﹣1.
第n个算式为:n(n+2)﹣(n+1)2=﹣1.
故答案为:4×6﹣52=24﹣25=﹣1;n(n+2)﹣(n+1)2=﹣1.
考点8
整式加减
例19(2020河北)有一电脑程序:每按一次按键,屏幕的区就会自动加上,同时区就会自动减去,且均显示化简后的结果.已知,两区初始显示的分别是25和-16,如图.
如,第一次按键后,,两区分别显示:
(1)从初始状态按2次后,分别求,两区显示的结果;
(2)从初始状态按4次后,计算,两区代数式的和,请判断这个和能为负数吗?说明理由.
解析:(1)A区显示结果为:,
B区显示结果为:;
(2)初始状态按4次后A显示为:
B显示为:
∴A+B=
=
=
∵恒成立,
∴和不能为负数.
四、易错点剖析
1、对单项式的定义理解不准致错
例1 下列式子中,是单项式的有( )(只填序号)
①a;②-2;③x+3y;④;⑤;⑥
错解: ①②④.
剖析:单项式的存在形式有以下几种:(1)单独的数;(2)单独的字母;(3)数与字母的乘积;(4)单独的字母或字母的乘积与数字的商.当有分母时,分母中出现了字母就一定不是单项式,注意π是一个数字而不是一个字母,这一点同学们一定要记清楚.
正解:①②⑥.
2、对单项式的系数理解不准致错
例2 单项式-y的系数为 .
错解: 1或0.
剖析:确定单项式的系数时,我们按照规范+省略的眼光来分析:
所谓的规范是指:(1)把单项式分成数×字母的形式;(2)省略字母后的因数就是系数.
所谓的省略是指:当系数时1时,数字1省略不写;当系数时-1时,数字1省略不写但是“-”却不能省略.所以-y=(-1)×(y),所以单项式-y的系数为-1.
正解:-1.
3、对单项式的次数理解不准致错
例3 在下列代数式中,次数为3的单项式是( )
A.x
B. C. D.3xy
错解:
选B或选C.
剖析: 确定单项式的次数时,我们的思考顺序是:
(1)首先确定它是单项式;(2)确定单项式中字母的种数;
(3)确定每种字母的指数;(4)确定每种字母指数的和.解答时,一定要严格落实上面的要求.因为是多项式,不是单项式,所以不符合题意.其余如下:
所以符合的是A.
正解: 选A.
4、对同类项的定义理解不准致错
例4 下列各式是同类项的是(
)
①2和2;②-25和;③2和4;④-和5
A.②③④.
B. ②③.
C. ②④.
D.①②③.
错解: 选A或选B.
剖析:判断两个式子是同类项时,一定注意以下几点:
1.两个式子必须都是单项式;2.
两个单项式中的字母种数必须相同;
3.
同一个字母在单项式中的指数必须相同;
4.同类项与单项式的系数无
;5.
同类项与字母顺序无关;
6.
具体的数,不论其呈现形式如何,都是特殊的同类项.
正解:①中的两个单项式中字母的种数不同,所以一定不是同类项;②中的两个式子都标示的是数,所以一定是同类项;③中字母的种数相同,但是相同字母的指数不同,所以一定不是同类项;④中字母的种数相同,相同的字母的指数也相同,只是顺序不同,根据乘法交换律可以变形为-和5,所以一定是同类项.所以应该选C.
5、对合并同类项的实质把握不准致错
例5 下列合并同类项的结果是错误的有 .(只填序号)
①2a+3=5;②3x+4x=7;③5xy-4xy=1;
④ax-xa=0;⑤4y-5y=-1y;⑥3a-a=2a.
错解: ③.
剖析:合并同类项的实质是把同类项的系数相加或相减,同类项中的字母及其指数保持不变.①中的两个式子根本不是同类项,谈不上合并同类项,所以其计算结果必然是错误的;②中的两个式子是同类项,可以进行合并,系数相加为7没有错,错在把字母的指数也进行了加法运算,正确的结果应该是3x+4x=7x;③中的两个式子也是同类项,因此可以进行合并,系数相减为1也是正确的,但是不能把字母省去,正确的结果是5xy-4xy=xy,系数1要省去;④正确;⑤计算的结果没有错,错在没有按照课本的要求去记结果,当系数的绝对值是1时,数字1要省略不写,所以正确结果为4y-5y=-y;⑥中的结果是正确的,但是错在结果的书写上,当带分数与字母相乘时,带分数一定要化成假分数,所以正确结果为a.
正解:①②③⑤⑥.
6、对去括号的法则理解不准致错
例6 计算-3(x-2y-1)的结果正确的是( )
A.-3x-2y-1
B. -3x-6y-1
C.-3x+6y-3
D.-3x+6y+3
错解: 选A或选B或选C.
剖析:当括号前面有系数,去括号时,要先把系数逐项乘进括号中,特别是当系数是负数时,一定要用这个负数去乘以括号里的每一项,不能漏项,把"-( )"型去括号转化成"+(
)”型去括号,这样就可避免一些错误的出现.
正解:-3(x-2y-1)={[(-3)×1]x+[(-3)×(-2)]y+[(-3)×(-1)]=(-3x+6y+3)=-3x+6y+3,所以选择D.
知识思维导图
二、知识梳理
1.字母可以表示
(
)
A.任何数
B.有理数
C.非负数
D.实数
2.代数式中含有数字或表示数的之外,通常还含有(
)
A.字母
加法B.字母
减法C.字母
乘、除、乘方D.字母
运算符号
3.代数式中的运算符号,主要包含加,减,(
)
A.乘、除B.乘、乘方C.乘、除、乘方D.乘、除、乘方、开方
4.单独的一个或一个,也是代数式.(
)
A.数、aB.字母、3C.数
字母D.数
运算符号
5.数值转换机是用来
(
)
A.列代数式B.编程序C.计算代数式的值D.求数的绝对值
6.一般地,用代替代数式中的,计算所得结果叫做代数式的值.(
)
A.字母
数B.数值
字母C.运算符号
字母D.数值
运算符号
7.关于单项式的描述,错误的是
(
)
A.数与字母乘积的代数式B.单独的一个数是单项式
C.单独的一个字母时单项式D.相同字母的积不是单项式
8.单项式中叫做单项式的系数,所有字母的叫做单项式的次数(
)
A.数字
指数和B.数字因数
指数和C.数字
指数差D.数字因数
指数差
9.对单项式的系数,指数两省一不一零的理解
当单项式的系数为或时,通常省略不写,但的符号不能省略,此外,字母因数的指数如果是,通常也省略不写;单独的一个非零数的次数是.
10.几个单项式的叫做多项式.(
)
A.和B.差C.积D.商
11.在多项式中,每个叫做多项式的项,不含的项叫做常数项.(
)
A.代数式
字母B.单项式
字母C.字母
字母D.单项式
单项式
12.和统称整式.
(
)
A.单项式
代数式B.多项式
代数式C.单项式多项式D.代数式
代数式
13.所含相同,并且的指数也的项叫做同类项.(
)
A.字母
相同字母
相同B.字母
相同字母不相同
C.字母
不同字母
相同
D.字母
不同字母不相同
14.下列说法,正确的是
(
)
A.所有字母都是同类项B.所有多项式都是同类项
C.所有常数项都是同类项D.所有单项式都是同类项
15.把合并成一项,叫做合并同类项.
(
)
A.单项式B.多项式C.整式D.同类项
16.合并同类项的依据是
(
)
A.乘法对加法的结合律B.乘法对加法的分配律C.加法的交换律D.加法的结合律
17.合并同类项时,把同类项的相加,字母和字母的不变.(
)
A.项
次数B.系数
指数C.指数
指数D.系数,系数
18.括号前是“+”号,把和它前面的“+”号去掉后,原来括号里各项的符号都(
)
A.括号
改变B.括号
不改变C.系数
改变D.指数
不改变
19.括号前是“-”号,把和它前面的“-”号去掉后,原来括号里各项的符号都(
)
A.括号
改变
B.括号
不改变C.系数
改变
D.指数
不改变
20.进行整式加减运算时,如果遇到括号,要先,再
(
)
A.去掉括号
把指数相加B.去掉括号
把系数相加
C.去掉括号
合并同类项D.去掉括号
合并单项式
三、知识应用
考点
1:布列代数式
例1(2020长沙).某数学老师在课外活动中做了一个有趣的游戏:首先发给A,B,C三个同学相同数量的扑克牌(假定发到每个同学手中的扑克牌数量足够多),然后依次完成下列三个步骤:
第一步,A同学拿出三张扑克牌给B同学;
第二步,C同学拿出三张扑克牌给B同学;
第三步,A同学手中此时有多少张扑克牌,B同学就拿出多少张扑克牌给A同学,
请你确定,最终B同学手中剩余的扑克牌的张数为___________________.
题意剖析:
以扑克游戏为问题背景,让学生感到亲切,不反感,反映了数学源于生活的思想,同时,为了解决问题,需要用到字母表示数的思想,学会熟练规范进行代数式的布列,巩固了相应的数学知识,落实了让学生在玩中学的课标学习目标,值得点赞!
解法直播:
解法1:设每个同学扑克牌的数量都是;
第一步,A同学的扑克牌的数量是,B同学的扑克牌的数量是;
第二步,B同学的扑克牌的数量是,C同学的扑克牌的数量是;
第三步,A同学的扑克牌的数量是2(),B同学的扑克牌的数量是();
∴B同学手中剩余的扑克牌的数量是:().故答案为:.
点评:按照题目的操作顺序,步步为营,紧紧指向目标,是常用的求解思路.
解法2:设每个同学扑克牌的数量都是,列表如下:
所以答案为9.
点评:列表法是数学解题的一种非常实用有效的解题方法,最大特点是简洁,直观,易懂易操作,是值得同学们熟练掌握的好解题方法.
考点2:求代数式的值
(1)整体代入
例2(2020重庆B卷)已知a+b=4,则代数式1+的值为
(
)
A.3
B.1
C.0
D.-1
解析:因为=,a+b=4,所以原式=1+=3,所以选A.
点评:把握已知条件,梳理所求代数式的特点,选择整体代入求值是正确的选择.
(2)单一代入
例3(2020年黄岗)若|x-2|+=0,则-xy=
.
解:,,,,,
,故答案为:2.
点评:活用实数的非负性质,求得每个字母的值,为代数式的值计算提供支撑.
考点3:单项式
活动1:确定单项式的系数
例4(2019湖南怀化)单项式﹣5ab的系数是
( )
5
B.﹣5
C.2
D.﹣2
分析:单项式的一般结构是数字因数+字母因数,其中的数字因数叫做单项式的系数,注意系数一定要包含数的符号.特别地,单纯的数不能称系数,单独的字母其系数为1或-1,通常数字“1”省略不写,只写其符号代替.
解:-5ab的数字因数为-5,所以单项式-5ab的系数为-5,所以选B.
活动2:确定单项式的次数
例5(2019,山东淄博)单项式的次数是
.
分析:单项式的次数是所有字母指数的和,就现阶段的内容看,单项式的次数一定是正整数.
谨记字母的指数最小是1,如a的指数是1,绝对不是0,否则计算的结果一定是错误的.
解:因为a的次数是3,b的次数为2,所以单项式的次数为3+2=5,所以填5.
活动3:探索单项式中的变化规律
例6(2019?云南)按一定规律排列的单项式:,-,,-,,……第n个单项式是
(
)
A.
B.
C.
D.
分析:观察各单项式,发现奇数项系数为正,偶数项系数为负,所以可以用或(为大于等于1的整数)来控制系数的正负,指数为从3开始的奇数,所以指数部分规律为2n+1.整体处理即可得到答案.
解:观察可知,奇数项系数为正,偶数项系数为负,所以可以用或
(为大于等于1的整数)来控制系数的正负,指数为从3开始的奇数,所以指数部分规律为2n+1,所以选C.
活动4:阅读创新,提高自学能力
例7(2019湖南张家界)阅读下面的材料:
按照一定顺序排列着的一列数称为数列,数列中的每一个数叫做这个数列的项.排在第一位的数称为第一项,记为,排在第二位的数称为第二项,记为,依此类推,排在第n位的数称为第n项,记为.所以,数列的一般形式可以写成:,,,…,,….
一般地,如果一个数列从第二项起,每一项与它前一项的差等于同一个常数,那么这个数列叫做等差数列,这个常数叫做等差数列的公差,公差通常用d表示.如:数列1,3,5,7,…为等差数列,其中=1,=3,公差为d=2.根据以上材料,解答下列问题:
(1)等差数列5,10,15,…的公差d为 ,第5项是 .
(2)如果一个数列,,,…,,…,是等差数列,且公差为d,那么根据定义可得到-=d,﹣=d,-=d,…,-=d,….所以=+d,
=+d=(+d)+d=+2d,=+d=(+2d)+d=+3d,……
由此,请你填空完成等差数列的通项公式:=+( )d.
(3)﹣4041是不是等差数列﹣5,﹣7,﹣9…的项?如果是,是第几项?
分析:这是一道高中基础知识下移生成的阅读型考题,其意义有五:一是培养学生的阅读能力,这是解题的基础,题意都读不懂,更难说解题;二是培养学生的自学能力,学会理解题意,学会寻找解题方法;三是培养自我接受新鲜事物的能力,特别是接受新知识的能力,这是全面数学素养提升的基础;四是培养寻找系数与序号之间的变化规律的探索能力;培养学生学以致用的问题解决能力.
解:(1)根据题意得,d=10﹣5=5;因为=15,所以=+d=15+5=20,所以=+d=20+5=25,
所以应该填5;25.
(2)因为=+(2-1)d,=+d=(+d)+d=+2d=+(3-1)d,
=+d=(+2d)+d=+3d=+(4-1)d,……所以=+(n﹣1)d,所以应该填
n﹣1.
(3)因为等差数列﹣5,﹣7,﹣9…中,=-5,d=-7-(-5)=﹣2,所以=+(n﹣1)d=-5-2(n-1),因为﹣5﹣2(n﹣1)=﹣4041,解得:n=2019,符合题意,所以﹣4041是等差数列﹣5,﹣7,﹣9…的项,且它是此数列的第2019项.
考点4
同类型型
例8(2020贵州黔西南)若7与﹣的和为单项式,则=
.
解析:因为7与﹣的和为单项式,所以7与﹣是同类型,
所以x=3,y=2,所以==8.
点评:这是单项式与同类型两个基本概念之间的内在联系,抓住联系,将概念题目化,不仅考查了对单个概念的理解与应用,更注重了概念间的联系,实现了培养数学综合能力的解题的目标.
例9(2020苏州)若单项式与单项式是同类项,则________.
解析:因为单项式与单项式是同类项,所以m-1=2,n+1=2,
所以m=3,n=1,所以m+n=3+1=4;(2)所以m-1+n+1=2+2,所以m+n=4.
点评:同类项型概念题是中考的常考题型,也是基础性考题之一,解答时,注意如下几点:1.落实好两个对应即明确对应字母,后根据对应字母的指数对应相等构造出解题需要的等式;2.根据等式,完成对字母值的确定;3.化归为代数式的值问题求解思路,确定最终的结果.解答时,要注意用好两种求解思路:单字母值确定法,这是解题的同法,也是同学们最常用的方法;整体求值法,根据条件的特点,可将两个等式求和或求差,得到答案.
考点5多项式型
例10(2020年绵阳)若多项式x+(n-2)+1是关于x,y的三次多项式,则mn=.
解析:因为多项式x+(n-2)+1是关于x,y的三次多项式,所以n-2=0,
且|m-n|=2,所以n=2,|m-2|=2,所以m=4,n=2,或m=0,n=2,所以mn=8或mn=0.
点评:抓住多项式的次数定义是完成解题的根本依据,解答时,注意如下几点:
1.多项式的次数是多项式中每一个单项式次数的最高次数,具备最高次数的单项式可以不唯一;
2.熟记单项式次数的确定方法,各字母指数的和,为解题构造等式提供支撑;
3.掌握消除高于最高次数的项的基本方法:令该项的系数为0,0与任何数,任何式的积均为0,从而实现消项的目标.
考点6编程计算
1.以“0”为参照标准的单一代数式的编程计算
例11(2020江苏连云港)按照如图1所示的计算程序,若x=2,则输出的结果是
.
分析:编程计算,简洁但内涵丰富,解答时,需要准确理解编程计算的意义和计算原理,其基本结构为:输入值→代数式→转化为代数式的值→对照标准→符合→输出,不符合,代数式的值作为新输入值,进行再次流程计算,直到符合标准为止.
解析:
当x=2时,10-=10-=6>0,不符合标准,当x=6时,10-=10-=10-36=-26<0,符合标准,可以输出,所以输出的结果是-26.
点评:编程计算的实质是求代数式的值,是一种符合标准输出,不符合标准,代数式的值转化为输入值重新计算值的重复型计算题,理解编程计算的实质和意义是解题的关键.
2.分类输入两代数式的规律探索型编程计算
例12(2020贵州黔西南)如图2,是一个运算程序的示意图,若开始输入x的值为625,则
第2020次输出的结果为
.
分析:程序的基本特点,对输入数按照等于1和不等于1进行分类,后进行分类计算,通过反复的输入计算,寻找其中的基本规律,利用循环节的思想方法求解即可.
解析:当x=625时≠1,所以x=125;当x=125时≠1,所以x=25;
当x=25时≠1,所以x=5;当x=5时≠1,所以x=1;
当x=1时,x+4=5,当x=5时≠1,所以x=1;…依此类推,以5,1值进行循环,循环节为2,因为(2020﹣2)÷2=1010,所以第2020次的结果为1即输出的结果是1.
点评:解答时,不要急躁,通过进行多步计算,将问题转化为循环节问题,这是解题的关键.确定从第几步开始,循环节是多少,循环值的对应变化规律都是解题时必须要解决的问题,要熟练掌握.
考点7
规律探索
1.黑色三角形拼图摆放中寻找规律
例13(2020重庆A卷)把黑色三角形按如图所示的规律拼图案,其中第①个图案中有1个黑色三角形,第②个图案中有3个黑色三角形,第③个图案中有6个黑色三角形,…,按此规律排列下去,则第⑤个图案中黑色三角形的个数为
(
)
A.
10
B.
15
C.
18
D.
21
解析:∵第①个图案中黑色三角形的个数为1,第②个图案中黑色三角形的个数3=1+2,
第③个图案中黑色三角形的个数6=1+2+3,……,∴第⑤个图案中黑色三角形的个数为1+2+3+4+5=15,故选:B.
点评:选择正确的试题角度是解题的关键.从上而下,分层数,分别加,是解题的根本.
其一般性规律为:第n个图案中,黑三角形的个数:1+2+3+……+n=.
其计算思想恰好是高斯计算思想的再现,在寻找规律中,缅怀了数学名人.
2.正三角形拼图摆放中寻找规律
例14(2020山西)(3分)如图是一组有规律的图案,它们是由边长相等的正三角形组合而成,第1个图案有4个三角形,第2个图案有7个三角形,第3个图案有10个三角形…按此规律摆下去,第n个图案有
个三角形(用含n的代数式表示).
解法1:整体元分割法,列表思索如下:
所以第n个图案有(3n+1)个三角形.故答案为:(3n+1).
点评:此法采用图形整体元分解法,准确实施图形分割是解题的关键.这里也体现局部整体思维的智慧,实现了整体变化,局部稳定的解题探索.
解法2:上、下二层分割法
第一个图案数:2+1+1=4;第二个图案数:2×2+2+1=7;第三个图案数:3×2+3+1=10;
第四个图案数:4×2+4+1=13;…,第n个图案数:n×2+n+1=3n+1,.故答案为:(3n+1).
点评:合理分层使得规律发现更容易,更容易总结,这也体现了数学创新精神的课标要求,培养自我数学创新意识.
3.实心圆点摆放中寻找规律
例15(2020重庆B卷)下列图形都是由同样大小的实心圆点按一定规律组成的,其中第①个图形一共有5个实心圆点,第②个图形一共有8个实心圆点,第③个图形一共有11个实心圆点,?,按此规律排列下去,第⑥个图形中实心圆点的个数为
(
)
A.18
B.
19
C.20
D.21
解析:横、纵二层分割法探索列表如下:
所以第n个图案中,圆点数为(3n+2)个,当n=6时,3n+2=20,所以选C.
点评:科学分割图案,用序号分别表示横,纵圆点数是解题的关键.
4.菱形摆放中寻找规律
例16(2020贵州黔西南)如图图形都是由同样大小的菱形按照一定规律所组成的,其中第①
个图形中一共有3个菱形,第②个图形中一共有7个菱形,第③个图形中一共有13个菱形,…,
按此规律排列下去,第⑦个图形中菱形的个数为
.
解析:继续采用二层分割法
第①个图形中上层1,下层1+1,即1+1+1=3,一共有3个菱形;
第②个图形中上层1+2+1,下层2+1,即+2+1=7,一共有7个菱形;
第③个图形中上层1+2+3+2+1下层3+1,即+3+1=13,一共有33个菱形;
…,按此规律排列下去,
第n个图形中上层1+2+…+n+…+2+1,下层n+1,即+n+1,一共有(+n+1)个菱形;
所以第⑦个图形中菱形的个数为:+n+1=+7+1=57.所以答案为:57.
点评:上下二层分割法是解题的方法引领,代数式变形为序号为底数的自然数完全平方,是解题的关键,灵活变形是解题的创新灵魂所在.
例17(2020海南)海南黎锦有着悠久的历史,已被列入世界非物质文化遗产名录.如图是黎锦上的图案,每个图案都是由相同菱形构成的,若按照第1个图至第4个图中的规律编织图案,则第5个图中有 个菱形,第n个图中有
个菱形(用含n的代数式表示).
解析:∵第1个图中菱形的个数1=+;第2个图中菱形的个数5=+;
第3个图中菱形的个数13=+;第4个图中菱形的个数25=+
∴第5个图中菱形的个数为+=41,
第n个图中菱形的个数为+=2-2n+1,故答案为:41,2-2n+1.
点评:这个图示,实际上是勾股数的变式,这启示同学们,在常态学习时,不仅要注意式子的学习,更要掌握式子的形的意义,这样才能全面掌握,全面学习,继而实现数形结合的思想的提炼与渗透,实现培养数学核心素养的数学学习目标.
5.恒等式中寻找规律
例18(2020青海)(4分)观察下列各式的规律:
①1×3﹣22=3﹣4=﹣1;②2×4﹣32=8﹣9=﹣1;③3×5﹣42=15﹣16=﹣1.
请按以上规律写出第4个算式
.
用含有字母的式子表示第n个算式为
.
解析:④4×6﹣52=24﹣25=﹣1.
第n个算式为:n(n+2)﹣(n+1)2=﹣1.
故答案为:4×6﹣52=24﹣25=﹣1;n(n+2)﹣(n+1)2=﹣1.
考点8
整式加减
例19(2020河北)有一电脑程序:每按一次按键,屏幕的区就会自动加上,同时区就会自动减去,且均显示化简后的结果.已知,两区初始显示的分别是25和-16,如图.
如,第一次按键后,,两区分别显示:
(1)从初始状态按2次后,分别求,两区显示的结果;
(2)从初始状态按4次后,计算,两区代数式的和,请判断这个和能为负数吗?说明理由.
解析:(1)A区显示结果为:,
B区显示结果为:;
(2)初始状态按4次后A显示为:
B显示为:
∴A+B=
=
=
∵恒成立,
∴和不能为负数.
四、易错点剖析
1、对单项式的定义理解不准致错
例1 下列式子中,是单项式的有( )(只填序号)
①a;②-2;③x+3y;④;⑤;⑥
错解: ①②④.
剖析:单项式的存在形式有以下几种:(1)单独的数;(2)单独的字母;(3)数与字母的乘积;(4)单独的字母或字母的乘积与数字的商.当有分母时,分母中出现了字母就一定不是单项式,注意π是一个数字而不是一个字母,这一点同学们一定要记清楚.
正解:①②⑥.
2、对单项式的系数理解不准致错
例2 单项式-y的系数为 .
错解: 1或0.
剖析:确定单项式的系数时,我们按照规范+省略的眼光来分析:
所谓的规范是指:(1)把单项式分成数×字母的形式;(2)省略字母后的因数就是系数.
所谓的省略是指:当系数时1时,数字1省略不写;当系数时-1时,数字1省略不写但是“-”却不能省略.所以-y=(-1)×(y),所以单项式-y的系数为-1.
正解:-1.
3、对单项式的次数理解不准致错
例3 在下列代数式中,次数为3的单项式是( )
A.x
B. C. D.3xy
错解:
选B或选C.
剖析: 确定单项式的次数时,我们的思考顺序是:
(1)首先确定它是单项式;(2)确定单项式中字母的种数;
(3)确定每种字母的指数;(4)确定每种字母指数的和.解答时,一定要严格落实上面的要求.因为是多项式,不是单项式,所以不符合题意.其余如下:
所以符合的是A.
正解: 选A.
4、对同类项的定义理解不准致错
例4 下列各式是同类项的是(
)
①2和2;②-25和;③2和4;④-和5
A.②③④.
B. ②③.
C. ②④.
D.①②③.
错解: 选A或选B.
剖析:判断两个式子是同类项时,一定注意以下几点:
1.两个式子必须都是单项式;2.
两个单项式中的字母种数必须相同;
3.
同一个字母在单项式中的指数必须相同;
4.同类项与单项式的系数无
;5.
同类项与字母顺序无关;
6.
具体的数,不论其呈现形式如何,都是特殊的同类项.
正解:①中的两个单项式中字母的种数不同,所以一定不是同类项;②中的两个式子都标示的是数,所以一定是同类项;③中字母的种数相同,但是相同字母的指数不同,所以一定不是同类项;④中字母的种数相同,相同的字母的指数也相同,只是顺序不同,根据乘法交换律可以变形为-和5,所以一定是同类项.所以应该选C.
5、对合并同类项的实质把握不准致错
例5 下列合并同类项的结果是错误的有 .(只填序号)
①2a+3=5;②3x+4x=7;③5xy-4xy=1;
④ax-xa=0;⑤4y-5y=-1y;⑥3a-a=2a.
错解: ③.
剖析:合并同类项的实质是把同类项的系数相加或相减,同类项中的字母及其指数保持不变.①中的两个式子根本不是同类项,谈不上合并同类项,所以其计算结果必然是错误的;②中的两个式子是同类项,可以进行合并,系数相加为7没有错,错在把字母的指数也进行了加法运算,正确的结果应该是3x+4x=7x;③中的两个式子也是同类项,因此可以进行合并,系数相减为1也是正确的,但是不能把字母省去,正确的结果是5xy-4xy=xy,系数1要省去;④正确;⑤计算的结果没有错,错在没有按照课本的要求去记结果,当系数的绝对值是1时,数字1要省略不写,所以正确结果为4y-5y=-y;⑥中的结果是正确的,但是错在结果的书写上,当带分数与字母相乘时,带分数一定要化成假分数,所以正确结果为a.
正解:①②③⑤⑥.
6、对去括号的法则理解不准致错
例6 计算-3(x-2y-1)的结果正确的是( )
A.-3x-2y-1
B. -3x-6y-1
C.-3x+6y-3
D.-3x+6y+3
错解: 选A或选B或选C.
剖析:当括号前面有系数,去括号时,要先把系数逐项乘进括号中,特别是当系数是负数时,一定要用这个负数去乘以括号里的每一项,不能漏项,把"-( )"型去括号转化成"+(
)”型去括号,这样就可避免一些错误的出现.
正解:-3(x-2y-1)={[(-3)×1]x+[(-3)×(-2)]y+[(-3)×(-1)]=(-3x+6y+3)=-3x+6y+3,所以选择D.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
