江西省赣县第三中学2020-2021学年高二上学期12月月考数学(理)试卷 Word含答案
文档属性
| 名称 | 江西省赣县第三中学2020-2021学年高二上学期12月月考数学(理)试卷 Word含答案 | 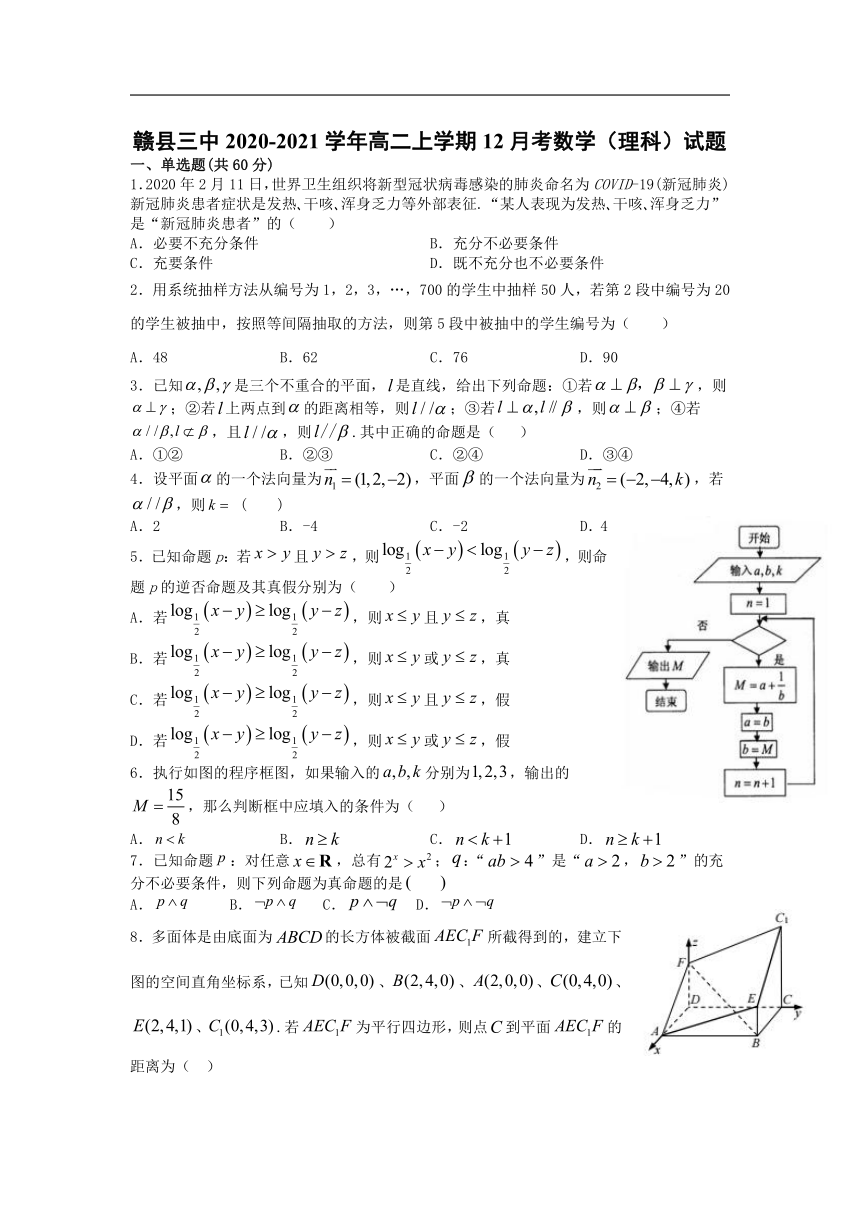 | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 09:28:00 | ||
图片预览




文档简介
赣县三中2020-2021学年高二上学期12月考数学(理科)试题
一、单选题(共60分)
1.2020年2月11日,世界卫生组织将新型冠状病毒感染的肺炎命名为COVID-19(新冠肺炎)新冠肺炎患者症状是发热?干咳?浑身乏力等外部表征.“某人表现为发热?干咳?浑身乏力”是“新冠肺炎患者”的( )
A.必要不充分条件 B.充分不必要条件
C.充要条件 D.既不充分也不必要条件
2.用系统抽样方法从编号为1,2,3,…,700的学生中抽样50人,若第2段中编号为20的学生被抽中,按照等间隔抽取的方法,则第5段中被抽中的学生编号为( )
A.48 B.62 C.76 D.90
3.已知是三个不重合的平面,是直线,给出下列命题:①若,则;②若上两点到的距离相等,则;③若,则;④若,且,则.其中正确的命题是( )
A.①② B.②③ C.②④ D.③④
4.设平面的一个法向量为,平面的一个法向量为,若,则 ( )
A.2 B.-4 C.-2 D.4
5.已知命题p:若且,则,则命题p的逆否命题及其真假分别为( )
A.若,则且,真
B.若,则或,真
C.若,则且,假
D.若,则或,假
6.执行如图的程序框图,如果输入的分别为,输出的,那么判断框中应填入的条件为( )
A. B. C. D.
7.已知命题:对任意,总有;:“”是“,”的充分不必要条件,则下列命题为真命题的是
A. B. C. D.
8.多面体是由底面为的长方体被截面所截得到的,建立下图的空间直角坐标系,已知、、、、、.若为平行四边形,则点到平面的距离为( )
A. B. C. D.
9.齐王有上等、中等、下等马各一匹,田忌也有上等、中等、下等马各一匹.田忌的上等马优于齐王的中等马,劣于齐王的上等马;田忌的中等马优于齐王的下等马,劣于齐王的中等马,田忌的下等马劣于齐王的下等马.现在从双方的马匹中随机各选一匹进行一场比赛,若有优势的马一定获胜,则齐王的马获胜得概率为( )
A. B. C. D.
10.将半径为,圆心角为的扇形围成一个圆锥,则该圆锥的内切球的体积为( )
A. B. C. D.
11.如图,在正四棱柱中, 是侧面内的动点,且记与平面所成的角为,则的最大值为( )
A. B. C. D.
12.设、、…、为平面内的个点,在平面内的所有点中,若点到、、…、点的距离之和最小,则称点为、、…、点的一个“中位点”,有下列命题:①、、三个点共线,在线段上,则是、、的中位点;②直角三角形斜边的中点是该直线三角形三个顶点的中位点;③若四个点、、、共线,则它们的中位点存在且唯一;④梯形对角线的交点是该梯形四个顶点的唯一中位点;其中的真命题是( )
A.②④ B.①② C.①④ D.①③④
二、填空题(共20分)
13.在空间直角坐标系中,点关系平面对称的坐标为,关于轴对称的点坐标为,则_____.
14.若在区间上随机取一个数,则事件“”发生的概率是______.
15.有以下命题:
①存在实数,,使得;
②“,”的否定是“存在,”;
③掷一枚质地均匀的正方体骰子,向上的点数不小于3的概率为;
④在闭区间上取一个随机数,则的概率为.
其中所有的真命题为________.(填写所有正确的结论序号)
16.已知三棱锥的各顶点都在球面上,,平面,,,若该球的体积为,则三棱锥的表面积为__________.
三、解答题(共70分)
17.(本题10分) 已知向量,.
(1)若,求实数;
(2)若向量与所成角为锐角,求实数的范围.
18.(本题12分)设命题:实数满足,其中;命题:实数满足.
(1)若,且为真,求实数的取值范围;
(2)若是的充分不必要条件,求实数的取值范围.
19.每年8月8日是我国全民健身日,其主题是:新时代全民健身动起来.某市为了解全民健身情况,随机从某小区居民中抽取了40人,将他们的年龄分成7段:[10,20),[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]后得到如图所示的频率分布直方图.
(1)试求这40人年龄的平均数、中位数的估计值;
(2)(i)若从样本中年龄在[50,70)的居民中任取2人赠送健身卡,求这2人中至少有1人年龄不低于60岁的概率;
(ⅱ)已知该小区年龄在[10,80]内的总人数为2000,若18岁以上(含18岁)为成年人,试估计该小区年龄不超过80岁的成年人人数.
20.如图,在梯形中,,,,现将沿翻折成直二面角.
(Ⅰ)证明:;
(Ⅱ)若异面直线与所成角的余弦值为,求二面角余弦值的大小.
21.已知,命題对任意,不等式恒成立;命题存在,使得成立.
(1)若为真命题,求的取值范围;
(2)若为假,为真,求的取值范围.
22.在四棱锥中,平面,,,,,,是的中点,在线段上,且满足.
(1)求证:平面;
(2)求二面角的余弦值;
(3)在线段上是否存在点,使得与平面所成角的余弦值是,若存在,求出的长;若不存在,请说明理由.
高二上学期12月考数学(理科)参考答案
A 2.B 3.D 4.D 5.D 6.C 7.D 8.C 9.D 10.A 11.B
12.C ①若三个点共线,在线段上,根据两点之间线段最短,
则是的中位点,正确;
②举一个反例,如边长为的直角三角形,此直角三角形的斜边的中点到三个顶点的距离之和为,而直角顶点到三个顶点的距离之和为7,
∴直角三角形斜边的中点不是该直角三角形三个顶点的中位点;故错误;
③若四个点共线,则它们的中位点是中间两点连线段上的任意一个点,故它们的中位点存在但不唯一;故错误;
④如图,在梯形中,对角线的交点是任意一点,则根据三角形两边之和大于第三边得,
∴梯形对角线的交点是该梯形四个顶点的唯一中位点.正确.
故①④正确.故选:C
13. 14. 15.①②④
16.27 如图所示,因为平面,所以,,,
因为,,所以平面,所以,
设的中点为,则,所以为三棱锥外接球的球心,
由题知,解得,所以,
在中,,,所以,
在中,,
在中,,
所以三棱锥的表面积为
.故答案为27.
17.(1);(2)且.
(1)由已知可得,,,因为,所以,可得.
(2)由(1)知,,,因为向量与所成角为锐角,所以,解得,
又当时,,可得实数的范围为且.
18.(1); (2).
(Ⅰ)对于命题:由得,
又,∴,当时,,即为真时实数x的取值范围是.
由已知为真时实数的取值范围是.
若为真,则真且真,∴实数的取值范围是.
(Ⅱ)是的充分不必要条件,即,且,
设,,则,
又,,
则且,∴实数的取值范围是.
19.(1) 平均数37,中位数为35;(2) (ⅰ);(ⅱ)该小区年龄不超过80岁的成年人人数约为2000×0.88=1760.
(1)平均数.
前三组的频率之和为0.15+0.2+0.3=0.65,故中位数落在第3组,设中位数为x,
则(x-30)×0.03+0.15+0.2=0.5,解得x=35,即中位数为35.
(2)(ⅰ)样本中,年龄在[50,70)的人共有40×0.15=6人,其中年龄在[50,60)的有4人,设为a,b,c,d,年龄在[60,70)的有2人,设为x,y.
则从中任选2人共有如下15个基本事件:(a,b),(a,c),(a,d),(a,x),(a,y),(b,c),(b,d),(b,x),(b,y),(c,d),(c,x),(c,y),(d,x),(d,y),(x,y).
至少有1人年龄不低于60岁的共有如下9个基本事件:
(a,x),(a,y),(b,x),(b,y),(c,x),(c,y),(d,x),(d,y),(x,y).
记“这2人中至少有1人年龄不低于60岁”为事件A,
故所求概率.
(ⅱ)样本中年龄在18岁以上的居民所占频率为1-(18-10)×0.015=0.88,
故可以估计,该小区年龄不超过80岁的成年人人数约为2000×0.88=1760.
20. (Ⅰ)详见解析(Ⅱ)
(Ⅰ)取的中点,连结.∵,,
∴,,∴四边形是平行四边形,
∴,∴,∴,即.
又平面平面,且两平面的交线为,∴平面,
又平面,∴.
(Ⅱ)取的中点,连结,则.
∴,且,∴,,两两互相垂直.
以为原点,,,为,,轴的正方向建立空间直角坐标系.设,则,,,,∴,.
由异面直线与所成角的余弦值为,得,解得.
易得平面的一个法向量为,∴设平面的一个法向量为,
又,,由,得,
取,得,,故,,
∴二面角的余弦值.
21.(1);(2)
(1)对任意,不等式恒成立,
当,由对数函数的性质可知当时,的最小值为,
,解得.
因此,若为真命题时,的取值范围是.
(2)存在,使得成立,.
命题为真时,,且为假,或为真,
,中一个是真命题,一个是假命题.
当真假时,则解得;
当假真时,,即.
综上所述,的取值范围为.
22.(1)见解析;(2);(3)
(1)由题意可得,,两两互相垂直,如果,以为原点,,,分别是,,轴建立空间直角坐标系,则,,,,设平面的法向量为,
∴,令∴又,∴,∴平面∴ 平面
(2)设点坐标为则,,
由得,∴设平面的法向量为,
由得即令∴
又由图可知,该二面角为锐角故二面角的余弦值为
(3)设,,∴
∴∴
∵与平面所成角的余弦值是∴其正弦值为∴,整理得:
,解得:,(舍)
∴存在满足条件的点,,且
一、单选题(共60分)
1.2020年2月11日,世界卫生组织将新型冠状病毒感染的肺炎命名为COVID-19(新冠肺炎)新冠肺炎患者症状是发热?干咳?浑身乏力等外部表征.“某人表现为发热?干咳?浑身乏力”是“新冠肺炎患者”的( )
A.必要不充分条件 B.充分不必要条件
C.充要条件 D.既不充分也不必要条件
2.用系统抽样方法从编号为1,2,3,…,700的学生中抽样50人,若第2段中编号为20的学生被抽中,按照等间隔抽取的方法,则第5段中被抽中的学生编号为( )
A.48 B.62 C.76 D.90
3.已知是三个不重合的平面,是直线,给出下列命题:①若,则;②若上两点到的距离相等,则;③若,则;④若,且,则.其中正确的命题是( )
A.①② B.②③ C.②④ D.③④
4.设平面的一个法向量为,平面的一个法向量为,若,则 ( )
A.2 B.-4 C.-2 D.4
5.已知命题p:若且,则,则命题p的逆否命题及其真假分别为( )
A.若,则且,真
B.若,则或,真
C.若,则且,假
D.若,则或,假
6.执行如图的程序框图,如果输入的分别为,输出的,那么判断框中应填入的条件为( )
A. B. C. D.
7.已知命题:对任意,总有;:“”是“,”的充分不必要条件,则下列命题为真命题的是
A. B. C. D.
8.多面体是由底面为的长方体被截面所截得到的,建立下图的空间直角坐标系,已知、、、、、.若为平行四边形,则点到平面的距离为( )
A. B. C. D.
9.齐王有上等、中等、下等马各一匹,田忌也有上等、中等、下等马各一匹.田忌的上等马优于齐王的中等马,劣于齐王的上等马;田忌的中等马优于齐王的下等马,劣于齐王的中等马,田忌的下等马劣于齐王的下等马.现在从双方的马匹中随机各选一匹进行一场比赛,若有优势的马一定获胜,则齐王的马获胜得概率为( )
A. B. C. D.
10.将半径为,圆心角为的扇形围成一个圆锥,则该圆锥的内切球的体积为( )
A. B. C. D.
11.如图,在正四棱柱中, 是侧面内的动点,且记与平面所成的角为,则的最大值为( )
A. B. C. D.
12.设、、…、为平面内的个点,在平面内的所有点中,若点到、、…、点的距离之和最小,则称点为、、…、点的一个“中位点”,有下列命题:①、、三个点共线,在线段上,则是、、的中位点;②直角三角形斜边的中点是该直线三角形三个顶点的中位点;③若四个点、、、共线,则它们的中位点存在且唯一;④梯形对角线的交点是该梯形四个顶点的唯一中位点;其中的真命题是( )
A.②④ B.①② C.①④ D.①③④
二、填空题(共20分)
13.在空间直角坐标系中,点关系平面对称的坐标为,关于轴对称的点坐标为,则_____.
14.若在区间上随机取一个数,则事件“”发生的概率是______.
15.有以下命题:
①存在实数,,使得;
②“,”的否定是“存在,”;
③掷一枚质地均匀的正方体骰子,向上的点数不小于3的概率为;
④在闭区间上取一个随机数,则的概率为.
其中所有的真命题为________.(填写所有正确的结论序号)
16.已知三棱锥的各顶点都在球面上,,平面,,,若该球的体积为,则三棱锥的表面积为__________.
三、解答题(共70分)
17.(本题10分) 已知向量,.
(1)若,求实数;
(2)若向量与所成角为锐角,求实数的范围.
18.(本题12分)设命题:实数满足,其中;命题:实数满足.
(1)若,且为真,求实数的取值范围;
(2)若是的充分不必要条件,求实数的取值范围.
19.每年8月8日是我国全民健身日,其主题是:新时代全民健身动起来.某市为了解全民健身情况,随机从某小区居民中抽取了40人,将他们的年龄分成7段:[10,20),[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]后得到如图所示的频率分布直方图.
(1)试求这40人年龄的平均数、中位数的估计值;
(2)(i)若从样本中年龄在[50,70)的居民中任取2人赠送健身卡,求这2人中至少有1人年龄不低于60岁的概率;
(ⅱ)已知该小区年龄在[10,80]内的总人数为2000,若18岁以上(含18岁)为成年人,试估计该小区年龄不超过80岁的成年人人数.
20.如图,在梯形中,,,,现将沿翻折成直二面角.
(Ⅰ)证明:;
(Ⅱ)若异面直线与所成角的余弦值为,求二面角余弦值的大小.
21.已知,命題对任意,不等式恒成立;命题存在,使得成立.
(1)若为真命题,求的取值范围;
(2)若为假,为真,求的取值范围.
22.在四棱锥中,平面,,,,,,是的中点,在线段上,且满足.
(1)求证:平面;
(2)求二面角的余弦值;
(3)在线段上是否存在点,使得与平面所成角的余弦值是,若存在,求出的长;若不存在,请说明理由.
高二上学期12月考数学(理科)参考答案
A 2.B 3.D 4.D 5.D 6.C 7.D 8.C 9.D 10.A 11.B
12.C ①若三个点共线,在线段上,根据两点之间线段最短,
则是的中位点,正确;
②举一个反例,如边长为的直角三角形,此直角三角形的斜边的中点到三个顶点的距离之和为,而直角顶点到三个顶点的距离之和为7,
∴直角三角形斜边的中点不是该直角三角形三个顶点的中位点;故错误;
③若四个点共线,则它们的中位点是中间两点连线段上的任意一个点,故它们的中位点存在但不唯一;故错误;
④如图,在梯形中,对角线的交点是任意一点,则根据三角形两边之和大于第三边得,
∴梯形对角线的交点是该梯形四个顶点的唯一中位点.正确.
故①④正确.故选:C
13. 14. 15.①②④
16.27 如图所示,因为平面,所以,,,
因为,,所以平面,所以,
设的中点为,则,所以为三棱锥外接球的球心,
由题知,解得,所以,
在中,,,所以,
在中,,
在中,,
所以三棱锥的表面积为
.故答案为27.
17.(1);(2)且.
(1)由已知可得,,,因为,所以,可得.
(2)由(1)知,,,因为向量与所成角为锐角,所以,解得,
又当时,,可得实数的范围为且.
18.(1); (2).
(Ⅰ)对于命题:由得,
又,∴,当时,,即为真时实数x的取值范围是.
由已知为真时实数的取值范围是.
若为真,则真且真,∴实数的取值范围是.
(Ⅱ)是的充分不必要条件,即,且,
设,,则,
又,,
则且,∴实数的取值范围是.
19.(1) 平均数37,中位数为35;(2) (ⅰ);(ⅱ)该小区年龄不超过80岁的成年人人数约为2000×0.88=1760.
(1)平均数.
前三组的频率之和为0.15+0.2+0.3=0.65,故中位数落在第3组,设中位数为x,
则(x-30)×0.03+0.15+0.2=0.5,解得x=35,即中位数为35.
(2)(ⅰ)样本中,年龄在[50,70)的人共有40×0.15=6人,其中年龄在[50,60)的有4人,设为a,b,c,d,年龄在[60,70)的有2人,设为x,y.
则从中任选2人共有如下15个基本事件:(a,b),(a,c),(a,d),(a,x),(a,y),(b,c),(b,d),(b,x),(b,y),(c,d),(c,x),(c,y),(d,x),(d,y),(x,y).
至少有1人年龄不低于60岁的共有如下9个基本事件:
(a,x),(a,y),(b,x),(b,y),(c,x),(c,y),(d,x),(d,y),(x,y).
记“这2人中至少有1人年龄不低于60岁”为事件A,
故所求概率.
(ⅱ)样本中年龄在18岁以上的居民所占频率为1-(18-10)×0.015=0.88,
故可以估计,该小区年龄不超过80岁的成年人人数约为2000×0.88=1760.
20. (Ⅰ)详见解析(Ⅱ)
(Ⅰ)取的中点,连结.∵,,
∴,,∴四边形是平行四边形,
∴,∴,∴,即.
又平面平面,且两平面的交线为,∴平面,
又平面,∴.
(Ⅱ)取的中点,连结,则.
∴,且,∴,,两两互相垂直.
以为原点,,,为,,轴的正方向建立空间直角坐标系.设,则,,,,∴,.
由异面直线与所成角的余弦值为,得,解得.
易得平面的一个法向量为,∴设平面的一个法向量为,
又,,由,得,
取,得,,故,,
∴二面角的余弦值.
21.(1);(2)
(1)对任意,不等式恒成立,
当,由对数函数的性质可知当时,的最小值为,
,解得.
因此,若为真命题时,的取值范围是.
(2)存在,使得成立,.
命题为真时,,且为假,或为真,
,中一个是真命题,一个是假命题.
当真假时,则解得;
当假真时,,即.
综上所述,的取值范围为.
22.(1)见解析;(2);(3)
(1)由题意可得,,两两互相垂直,如果,以为原点,,,分别是,,轴建立空间直角坐标系,则,,,,设平面的法向量为,
∴,令∴又,∴,∴平面∴ 平面
(2)设点坐标为则,,
由得,∴设平面的法向量为,
由得即令∴
又由图可知,该二面角为锐角故二面角的余弦值为
(3)设,,∴
∴∴
∵与平面所成角的余弦值是∴其正弦值为∴,整理得:
,解得:,(舍)
∴存在满足条件的点,,且
同课章节目录
