利用空间向量求二面角
图片预览




文档简介
(共21张PPT)
课题:利用法向量求二面角
茂名市第十六中学:高二数学理科备课组
主讲人:吕宇云
四、教学过程的设计与实施
l
A
B
O
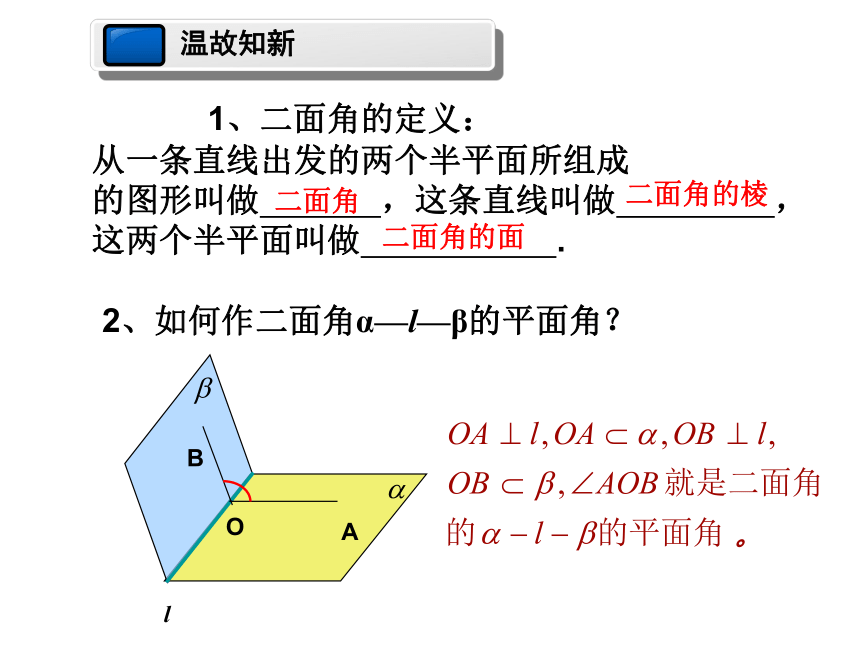
2、如何作二面角α—l—β的平面角?
温故知新
从一条直线出发的两个半平面所组成
的图形叫做 ,这条直线叫做 ,
这两个半平面叫做 .
二面角
二面角的棱
二面角的面
1、二面角的定义:
与面
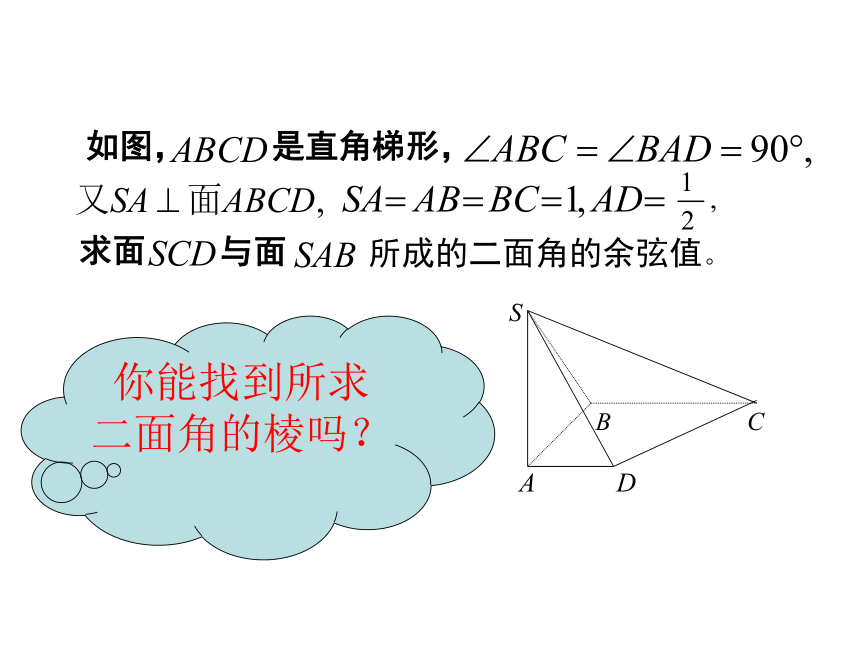
如图, 是直角梯形,
所成的二面角的余弦值。
求面
你能找到所求二面角的棱吗?
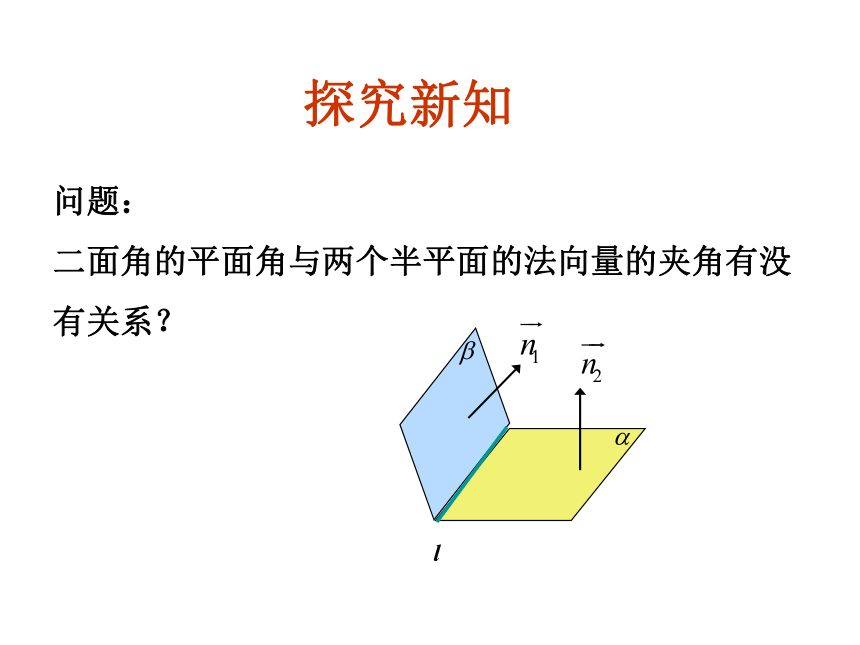
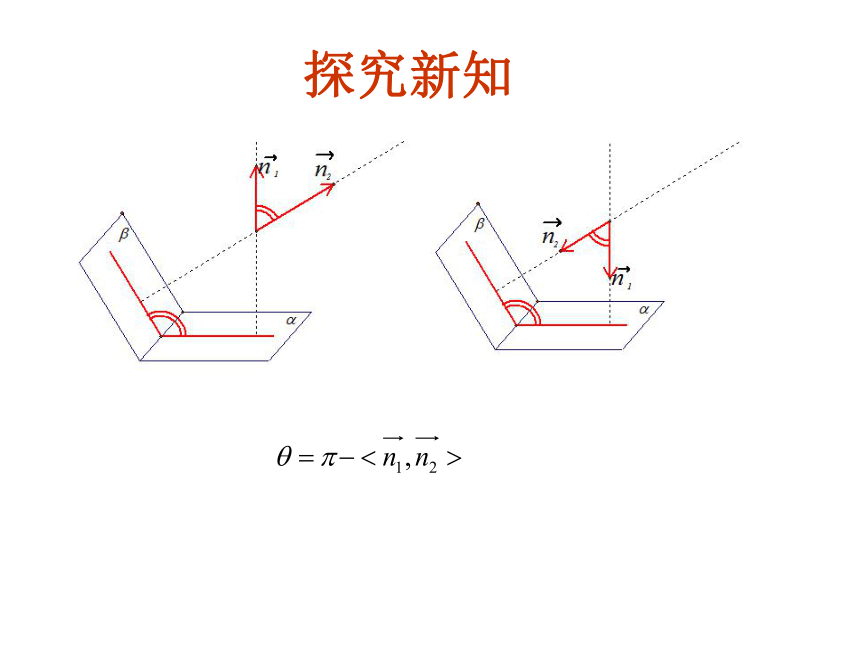
探究新知
问题: 二面角的平面角与两个半平面的法向量的夹角有没有关系?
l
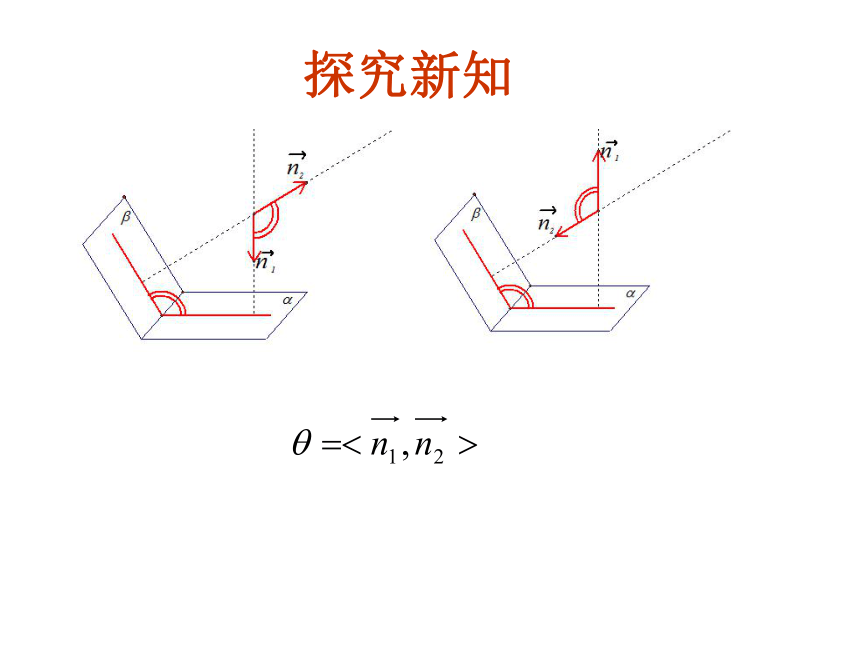
探究新知
探究新知
问题: 法向量的夹角与二面角的大小是相等或互补。
再次演示课件
探究新知
细心想一想,
你将有新发现!!
尝试:已知两平面的法向量分别为m=(0,1,0),
n=(0,1,1),则两平面所成的二面角为( )
A.45° B.135°
C.45°或135° D.90°
解析
即〈m,n〉=45°,其补角为135°.
∴两平面所成二面角为45°或135°.
C
练一练
与面
如图, 是直角梯形,
所成的锐二面角的余弦值。
求面
例题精讲
【审题指导】本题是求二面角的余弦值,可重点关注向量法求二面角的余弦值.本题的特点是图中没有出现两个平面的交线,不能直接利用二面角的平面角或者垂直于棱的向量的夹角解决,利用法向量的夹角解决体现了向量求解立体几何问题的优越性
解:
则
设
是面SCD的法向量,
与面
如图,ABCD是直角梯形,
所成的二面角的余弦值。
求面
建立如图所示的空间直角坐标系
则
启示:
求二面角的平面角可转化为求两法向量的夹角。
是平面SAB的法向量,
就是二面角的平面角,
所求锐二面角的余弦值为:
令z=1解之得
结论:
利用法向量求二面角的平面角避免了繁难的作、证二面角的过程。解题的关键是确定相关平面的法向量,如果图中的法向量没有直接给出,那么必须先创设法向量。
利用法向量求二面角的平面角的一般步骤:
建立坐标系
找点坐标
求法向量坐标
求两法向量夹角
定值
正方体ABCD—A1B1C1D1的棱长为2,点Q是BC的中点,求锐二面角A—DQ—A1的余弦值.
巩固练习:
x
y
z
小结:
1.利用法向量求二面角大小的优势:
避免了繁难的作、证二面角的过程,将几何问题转化为数值计算。
2.利用法向量求二面角大小的关键:
确定相关平面的法向量。
3.利用法向量求二面角大小的缺点:
计算量相对比较大。
课后思考 (2009·天津理,19)
如图,在五面体ABCDEF中,FA⊥
平面ABCD,AD∥BC∥FE,AB⊥
AD,M为EC的中点,AF=AB=BC=FE= .
(1)求异面直线BF与DE所成的角的大小;
(2)证明:平面AMD⊥平面CDE;
(3)求锐二面角A—CD—E的余弦值.
(1)解 如图所示,建立空间直
角坐标系,点A为坐标原点,设
AB=1,依题意得B(1,0,0),
C(1,1,0),D(0,2,0),E(0,1,1),F(0,0,1),
所以异面直线BF与DE所成的角的大小为60°.
(2)证明
又AM∩AD=A,故CE⊥平面AMD.而CE?平面
CDE,所以平面AMD⊥平面CDE.
(3)解 设平面CDE的法向量为u=(x,y,z),
令x=1,可得u=(1,1,1).
又由题设,平面ACD的一个法向量v=(0,0,1).
因为二面角A—CD—E为锐角,所以其余弦值为
课后作业:第111页A组:6、8
谢谢
课题:利用法向量求二面角
茂名市第十六中学:高二数学理科备课组
主讲人:吕宇云
四、教学过程的设计与实施
l
A
B
O
2、如何作二面角α—l—β的平面角?
温故知新
从一条直线出发的两个半平面所组成
的图形叫做 ,这条直线叫做 ,
这两个半平面叫做 .
二面角
二面角的棱
二面角的面
1、二面角的定义:
与面
如图, 是直角梯形,
所成的二面角的余弦值。
求面
你能找到所求二面角的棱吗?
探究新知
问题: 二面角的平面角与两个半平面的法向量的夹角有没有关系?
l
探究新知
探究新知
问题: 法向量的夹角与二面角的大小是相等或互补。
再次演示课件
探究新知
细心想一想,
你将有新发现!!
尝试:已知两平面的法向量分别为m=(0,1,0),
n=(0,1,1),则两平面所成的二面角为( )
A.45° B.135°
C.45°或135° D.90°
解析
即〈m,n〉=45°,其补角为135°.
∴两平面所成二面角为45°或135°.
C
练一练
与面
如图, 是直角梯形,
所成的锐二面角的余弦值。
求面
例题精讲
【审题指导】本题是求二面角的余弦值,可重点关注向量法求二面角的余弦值.本题的特点是图中没有出现两个平面的交线,不能直接利用二面角的平面角或者垂直于棱的向量的夹角解决,利用法向量的夹角解决体现了向量求解立体几何问题的优越性
解:
则
设
是面SCD的法向量,
与面
如图,ABCD是直角梯形,
所成的二面角的余弦值。
求面
建立如图所示的空间直角坐标系
则
启示:
求二面角的平面角可转化为求两法向量的夹角。
是平面SAB的法向量,
就是二面角的平面角,
所求锐二面角的余弦值为:
令z=1解之得
结论:
利用法向量求二面角的平面角避免了繁难的作、证二面角的过程。解题的关键是确定相关平面的法向量,如果图中的法向量没有直接给出,那么必须先创设法向量。
利用法向量求二面角的平面角的一般步骤:
建立坐标系
找点坐标
求法向量坐标
求两法向量夹角
定值
正方体ABCD—A1B1C1D1的棱长为2,点Q是BC的中点,求锐二面角A—DQ—A1的余弦值.
巩固练习:
x
y
z
小结:
1.利用法向量求二面角大小的优势:
避免了繁难的作、证二面角的过程,将几何问题转化为数值计算。
2.利用法向量求二面角大小的关键:
确定相关平面的法向量。
3.利用法向量求二面角大小的缺点:
计算量相对比较大。
课后思考 (2009·天津理,19)
如图,在五面体ABCDEF中,FA⊥
平面ABCD,AD∥BC∥FE,AB⊥
AD,M为EC的中点,AF=AB=BC=FE= .
(1)求异面直线BF与DE所成的角的大小;
(2)证明:平面AMD⊥平面CDE;
(3)求锐二面角A—CD—E的余弦值.
(1)解 如图所示,建立空间直
角坐标系,点A为坐标原点,设
AB=1,依题意得B(1,0,0),
C(1,1,0),D(0,2,0),E(0,1,1),F(0,0,1),
所以异面直线BF与DE所成的角的大小为60°.
(2)证明
又AM∩AD=A,故CE⊥平面AMD.而CE?平面
CDE,所以平面AMD⊥平面CDE.
(3)解 设平面CDE的法向量为u=(x,y,z),
令x=1,可得u=(1,1,1).
又由题设,平面ACD的一个法向量v=(0,0,1).
因为二面角A—CD—E为锐角,所以其余弦值为
课后作业:第111页A组:6、8
谢谢
