八年级数学下册第十九章一次函数章末复习四作业课件新版新人教版(共15张ppt)
文档属性
| 名称 | 八年级数学下册第十九章一次函数章末复习四作业课件新版新人教版(共15张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 613.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
第十九章 一次函数
章末复习(四) 一次函数
知识点一 函数图象的应用
1.(齐齐哈尔中考)“六一”儿童节前夕,某部队战士到福利院慰问儿童.战士们从营地出发,匀速步行前往文具店选购礼物,停留一段时间后,继续按原速步行到达福利院(营地、文具店、福利院三地依次在同一直线上).到达后因接到紧急任务,立即按原路匀速跑步返回营地(赠送礼物的时间忽略不计),下列图象能大致反映战士们离营地的距离S与时间x之间函数关系的是( B )
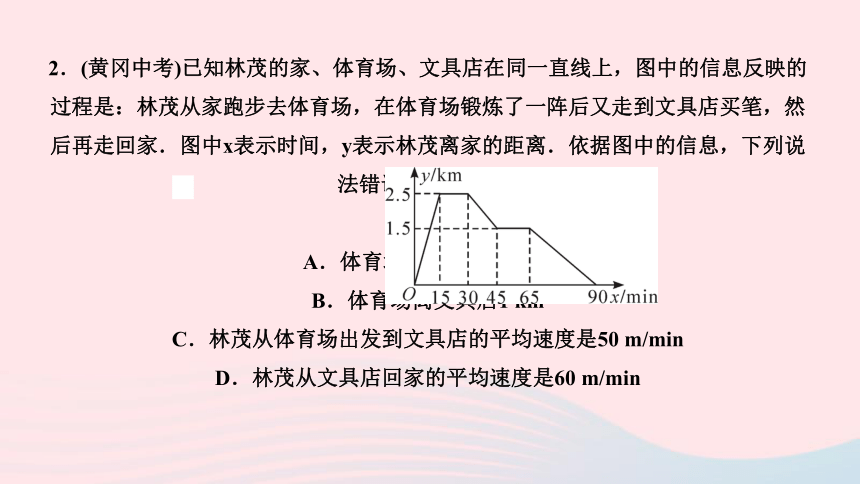
2.(黄冈中考)已知林茂的家、体育场、文具店在同一直线上,图中的信息反映的过程是:林茂从家跑步去体育场,在体育场锻炼了一阵后又走到文具店买笔,然后再走回家.图中x表示时间,y表示林茂离家的距离.依据图中的信息,下列说法错误的是( C )
A.体育场离林茂家2.5
km
B.体育场离文具店1
km
C.林茂从体育场出发到文具店的平均速度是50
m/min
D.林茂从文具店回家的平均速度是60
m/min
知识点二 求自变量的取值范围
3.下列函数中,自变量x的取值范围选取错误的是( D )
A.y=2x2中,x取全体实数
内江中考
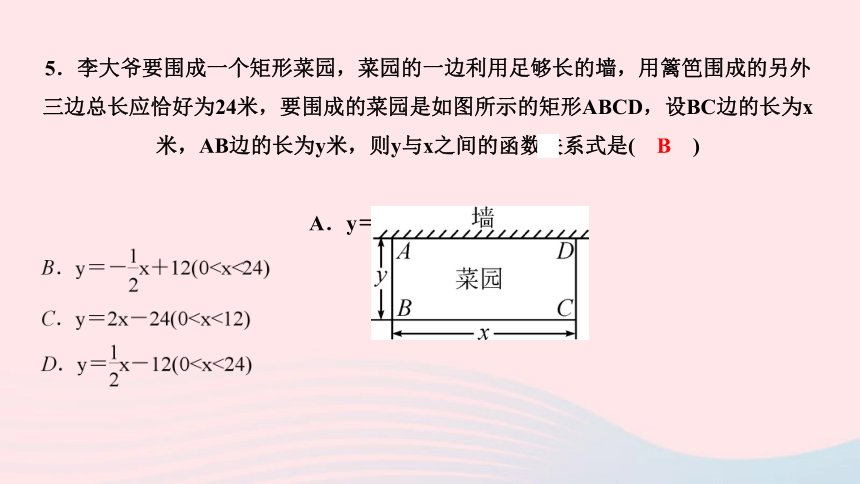
5.李大爷要围成一个矩形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长应恰好为24米,要围成的菜园是如图所示的矩形ABCD,设BC边的长为x米,AB边的长为y米,则y与x之间的函数关系式是( B )
A.y=-2x+24(0知识点三 确定函数解析式
6.把正比例函数y=2x的图象向右平移1个单位长度得到直线( B )
A.y=2x-1
B.y=2x-2
C.y=2x+1
D.y=2x+2
7.某一次函数的图象经过点(2,1),且与直线y=-2x+3相交于y轴上的同一点,求此一次函数的解析式.
解:设此一次函数的解析式为y=kx+b,∵y=kx+b与直线y=-2x+3相交于y轴上一点,∴交点坐标为(0,3),将(2,1),(0,3)代入y=kx+b,求得k=-1,b=3,∴此一次函数解析式为y=-x+3
知识点四 一次函数的图象与性质
8.(大庆中考)正比例函数y=kx(k≠0)的函数值y随着x增大而减小,则一次函数y=x+k的图象大致是( A )
9.(荆州中考)已知:将直线y=x-1向上平移2个单位长度后得到直线y=kx+b,则下列关于直线y=kx+b的说法正确的是( C )
A.经过第一、二、四象限
B.与x轴交于(1,0)
C.与y轴交于(0,1)
D.y随x的增大而减小
10.(绍兴中考)若三点(1,4),(2,7),(a,10)在同一直线上,则a的值等于( C )
A.-1
B.0
C.3
D.4
11.(苏州中考)若一次函数y=kx+b(k,b为常数,且k≠0)的图象经过点A(0,-1),B(1,1),则不等式kx+b>1的解为( D )
A.x<0
B.x>0
C.x<1
D.x>1
12.如图,已知函数y=x+1和y=ax+3图象交于点P,点P的横坐标为1,
13.(潍坊中考)当直线y=(2-2k)x+k-3经过第二、三、四象限时,则k的取值范围是__114.如图所示,一次函数y=x+5的图象经过点P(a,b)和Q(c,d),则a(c-d)-b(c-d)的值为__25__.
15.直线y=k1x+b1(k1>0)与y=k2x+b2(k2<0)相交于点(-2,0),且两直线与y轴围成的三角形的面积为4,那么b1-b2等于__4__.
知识点五 一次函数的应用
16.(东营中考)甲、乙两队参加了“端午情,龙舟韵”赛龙舟比赛,两队在比赛时的路程s(米)与时间t(秒)之间的函数图象如图所示,请你根据图象判断,下列说法正确的是( C )
A.乙队率先到达终点
B.甲队比乙队多走了126米
C.在47.8秒时,两队所走路程相等
D.从出发到13.7秒的时间段内,乙队的速度慢
17.(长春中考)已知A,B两地之间有一条270千米的长公路,甲、乙两车同时出发,甲车以60千米/时的速度沿此公路从A地匀速开往B地,乙车从B地沿此公路匀速开往A地,两车分别到达目的地后停止.甲、乙两车相距的路程y(千米)与甲车的行驶时间x(时)之间的函数关系如图所示.
(1)乙车的速度为__75__千米/时,a=__3.6__,b=__4.5__.
(2)求甲、乙两车相遇后,y与x之间的函数关系式.
(3)当甲车到达距B地70千米处时,求甲、乙两车之间的路程.
解:(1)乙车的速度为(270-60×2)÷2=75(千米/时),a=270÷75=3.6,b=270÷60=4.5;
(2)60×3.6=216(千米),当2<x≤3.6时,
18.为响应市政府“创建国家森林城市”的号召,某小区计划购进A,B两种树苗共17棵,已知A种树苗每棵80元,B种树苗每棵60元.
(1)若购进A,B两种树苗刚好用去1
220元,问购进A,B两种树苗各多少棵?
(2)若购进A种树苗a棵,所需费用为W元,求W与x的函数关系式;
(3)若购买B种树苗的数量少于A种树苗的数量,请你给出一种费用最省的方案,并求出该方案所需费用.
解:(1)设购进A种树苗x棵,则购进B种树苗(17-x)棵,根据题意,得80x+60(17-x
)=1
220,解得x=10,∴17-x=7,答:购进A种树苗10棵,B种树苗7棵
(2)W与a的函数关系式为W=80a+60(17-a)=20a+1
020
(3)由题意,得17-x<x,解得x>8.5且a为整数.∵W=20a+1
020,20>0,W随x的增大而增大,∴x=9时,W取最小值,即购买9棵A种树苗,8棵B种树苗时,费用最少,W=20×9+1
020=1
200,答:购买9棵A种树苗,8棵B种树苗时,费用最少,需要1
200元
第十九章 一次函数
章末复习(四) 一次函数
知识点一 函数图象的应用
1.(齐齐哈尔中考)“六一”儿童节前夕,某部队战士到福利院慰问儿童.战士们从营地出发,匀速步行前往文具店选购礼物,停留一段时间后,继续按原速步行到达福利院(营地、文具店、福利院三地依次在同一直线上).到达后因接到紧急任务,立即按原路匀速跑步返回营地(赠送礼物的时间忽略不计),下列图象能大致反映战士们离营地的距离S与时间x之间函数关系的是( B )
2.(黄冈中考)已知林茂的家、体育场、文具店在同一直线上,图中的信息反映的过程是:林茂从家跑步去体育场,在体育场锻炼了一阵后又走到文具店买笔,然后再走回家.图中x表示时间,y表示林茂离家的距离.依据图中的信息,下列说法错误的是( C )
A.体育场离林茂家2.5
km
B.体育场离文具店1
km
C.林茂从体育场出发到文具店的平均速度是50
m/min
D.林茂从文具店回家的平均速度是60
m/min
知识点二 求自变量的取值范围
3.下列函数中,自变量x的取值范围选取错误的是( D )
A.y=2x2中,x取全体实数
内江中考
5.李大爷要围成一个矩形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长应恰好为24米,要围成的菜园是如图所示的矩形ABCD,设BC边的长为x米,AB边的长为y米,则y与x之间的函数关系式是( B )
A.y=-2x+24(0
6.把正比例函数y=2x的图象向右平移1个单位长度得到直线( B )
A.y=2x-1
B.y=2x-2
C.y=2x+1
D.y=2x+2
7.某一次函数的图象经过点(2,1),且与直线y=-2x+3相交于y轴上的同一点,求此一次函数的解析式.
解:设此一次函数的解析式为y=kx+b,∵y=kx+b与直线y=-2x+3相交于y轴上一点,∴交点坐标为(0,3),将(2,1),(0,3)代入y=kx+b,求得k=-1,b=3,∴此一次函数解析式为y=-x+3
知识点四 一次函数的图象与性质
8.(大庆中考)正比例函数y=kx(k≠0)的函数值y随着x增大而减小,则一次函数y=x+k的图象大致是( A )
9.(荆州中考)已知:将直线y=x-1向上平移2个单位长度后得到直线y=kx+b,则下列关于直线y=kx+b的说法正确的是( C )
A.经过第一、二、四象限
B.与x轴交于(1,0)
C.与y轴交于(0,1)
D.y随x的增大而减小
10.(绍兴中考)若三点(1,4),(2,7),(a,10)在同一直线上,则a的值等于( C )
A.-1
B.0
C.3
D.4
11.(苏州中考)若一次函数y=kx+b(k,b为常数,且k≠0)的图象经过点A(0,-1),B(1,1),则不等式kx+b>1的解为( D )
A.x<0
B.x>0
C.x<1
D.x>1
12.如图,已知函数y=x+1和y=ax+3图象交于点P,点P的横坐标为1,
13.(潍坊中考)当直线y=(2-2k)x+k-3经过第二、三、四象限时,则k的取值范围是__1
15.直线y=k1x+b1(k1>0)与y=k2x+b2(k2<0)相交于点(-2,0),且两直线与y轴围成的三角形的面积为4,那么b1-b2等于__4__.
知识点五 一次函数的应用
16.(东营中考)甲、乙两队参加了“端午情,龙舟韵”赛龙舟比赛,两队在比赛时的路程s(米)与时间t(秒)之间的函数图象如图所示,请你根据图象判断,下列说法正确的是( C )
A.乙队率先到达终点
B.甲队比乙队多走了126米
C.在47.8秒时,两队所走路程相等
D.从出发到13.7秒的时间段内,乙队的速度慢
17.(长春中考)已知A,B两地之间有一条270千米的长公路,甲、乙两车同时出发,甲车以60千米/时的速度沿此公路从A地匀速开往B地,乙车从B地沿此公路匀速开往A地,两车分别到达目的地后停止.甲、乙两车相距的路程y(千米)与甲车的行驶时间x(时)之间的函数关系如图所示.
(1)乙车的速度为__75__千米/时,a=__3.6__,b=__4.5__.
(2)求甲、乙两车相遇后,y与x之间的函数关系式.
(3)当甲车到达距B地70千米处时,求甲、乙两车之间的路程.
解:(1)乙车的速度为(270-60×2)÷2=75(千米/时),a=270÷75=3.6,b=270÷60=4.5;
(2)60×3.6=216(千米),当2<x≤3.6时,
18.为响应市政府“创建国家森林城市”的号召,某小区计划购进A,B两种树苗共17棵,已知A种树苗每棵80元,B种树苗每棵60元.
(1)若购进A,B两种树苗刚好用去1
220元,问购进A,B两种树苗各多少棵?
(2)若购进A种树苗a棵,所需费用为W元,求W与x的函数关系式;
(3)若购买B种树苗的数量少于A种树苗的数量,请你给出一种费用最省的方案,并求出该方案所需费用.
解:(1)设购进A种树苗x棵,则购进B种树苗(17-x)棵,根据题意,得80x+60(17-x
)=1
220,解得x=10,∴17-x=7,答:购进A种树苗10棵,B种树苗7棵
(2)W与a的函数关系式为W=80a+60(17-a)=20a+1
020
(3)由题意,得17-x<x,解得x>8.5且a为整数.∵W=20a+1
020,20>0,W随x的增大而增大,∴x=9时,W取最小值,即购买9棵A种树苗,8棵B种树苗时,费用最少,W=20×9+1
020=1
200,答:购买9棵A种树苗,8棵B种树苗时,费用最少,需要1
200元
