1.5.1.2 【教案+测评】2019人教A版 必修 第一册 第五章 三角函数 第一节 任意角和弧度制 第二课时 弧度制
文档属性
| 名称 | 1.5.1.2 【教案+测评】2019人教A版 必修 第一册 第五章 三角函数 第一节 任意角和弧度制 第二课时 弧度制 |  | |
| 格式 | doc | ||
| 文件大小 | 866.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 20:45:05 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
教材考点
学习目标
核心素养
弧度制、角度制与弧度制的换算
了解弧度制的概念能进行角度与弧度之间的互化
数学抽象、数学运算
用弧度制表示终边相同的角
能用弧度制表示终边相同的角
数学运算
扇形的弧长与面积公式
理解弧度制下扇形的弧长与面积公式
数学运算
问题导学
预习教材P172-P175,并思考以下问题:
1.1弧度的角是如何定义的?
2.如何进行弧度与角度的换算?
3.以弧度为单位的扇形弧长、面积公式是什么?
1.度量角的两种制度
角度制
定义
用度作为单位来度量角的单位制
1度的角
1度的角等于周角的,记作1°
弧度制
定义
以弧度为单位来度量角的单位制
1弧度的角
长度等于半径长的圆弧所对的圆心角叫做1弧度的角.1弧度记作1
rad(rad可省略不写)
■微思考1
在大小不同的圆中,长度为1的弧所对的圆心角相等吗?
提示:不相等.这是因为长度为1的弧是指弧的长度为1,在大小不同的圆中,由于半径不同,所以圆心角也不同.
2.弧度数的计算与互化
(1)弧度数的计算
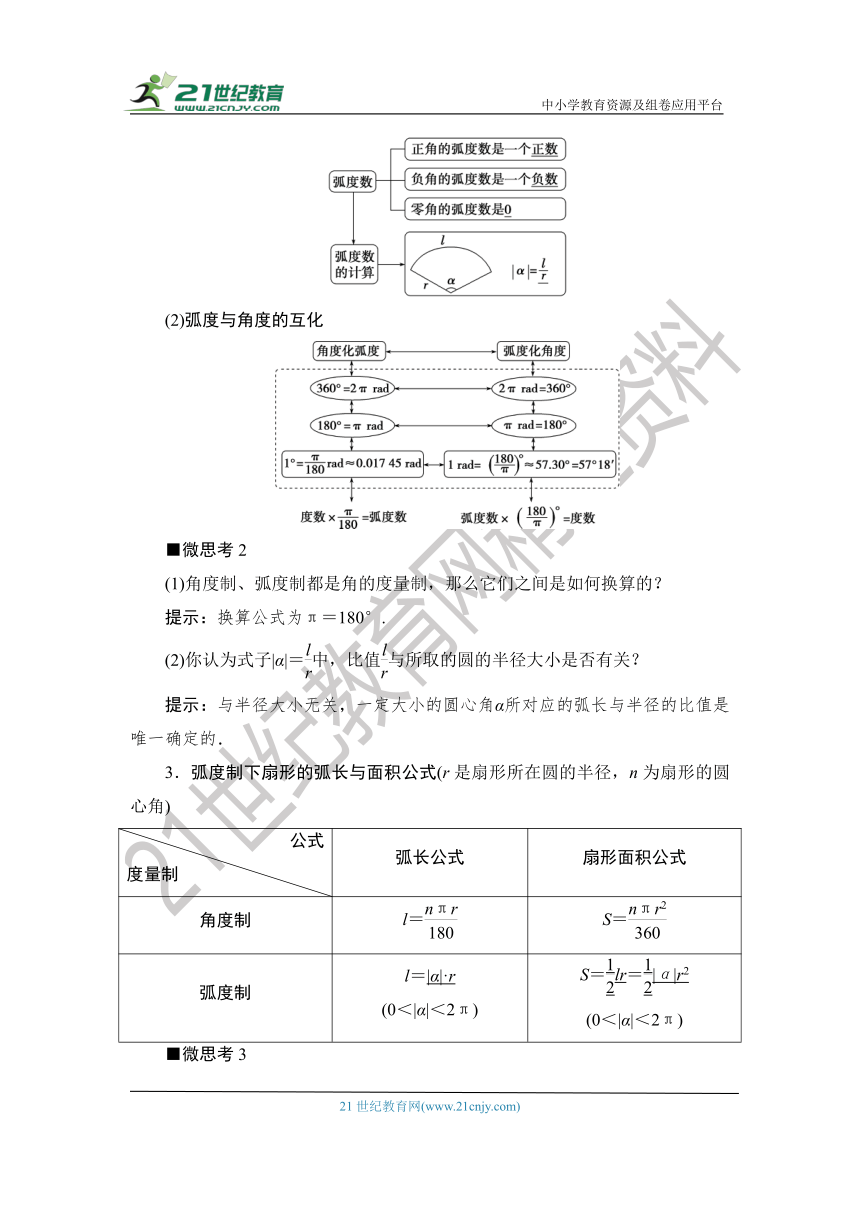
(2)弧度与角度的互化
■微思考2
(1)角度制、弧度制都是角的度量制,那么它们之间是如何换算的?
提示:换算公式为π=180°.
(2)你认为式子|α|=中,比值与所取的圆的半径大小是否有关?
提示:与半径大小无关,一定大小的圆心角α所对应的弧长与半径的比值是唯一确定的.
3.弧度制下扇形的弧长与面积公式(r是扇形所在圆的半径,n为扇形的圆心角)
公式 度量制
弧长公式
扇形面积公式
角度制
l=
S=
弧度制
l=|α|·r(0<|α|<2π)
S=lr=|α|r2(0<|α|<2π)
■微思考3
在应用扇形的面积公式S=|α|r2时,α的单位能是角度吗?
提示:不能,α的单位必须是弧度.
1.判断正误(正确的打“√”,错误的打“×”)
(1)1
rad的角比1°的角要大.( )
(2)用角度制和弧度制度量角,都与圆的半径有关.( )
(3)每个弧度制的角,都有唯一的角度制的角与之对应.( )
(4)1°的角是周角的,1
rad的角是周角的.( )
答案:(1)√ (2)× (3)√ (4)√
2.弧度化为角度是( )
A.278°
B.280°
C.288°
D.318°
答案:C
3.半径为2,圆心角为的扇形的面积是( )
A.
B.π
C.
D.
答案:C
4.(1)18°=________rad;(2)π=________.
答案:(1) (2)54°
探究点1 角度制与弧度制的互化
将下列角度与弧度进行互化:
(1)37°30′;(2)-216°;(3);(4)-.
【解】 (1)37°30′=37.5°=°=×=.
(2)-216°=-216×=-.
(3)=°=°=105°.
(4)-π=°=-396°.
角度制与弧度制的互化原则
(1)原则:牢记180°=π
rad,充分利用1°=
rad和1
rad=°进行换算.
(2)方法:设一个角的弧度数为α,角度数为n,则α
rad=°;n°=n·rad.
1.把下列角度化为弧度.
(1)-1
500°=________.
(2)67°30′=________.
解析:(1)-1
500°=-1
500×=-π.
(2)67°30′=67.5°=67.5×=.
答案:(1)- (2)
2.把下列弧度化为角度.
(1)=________.
(2)-=________.
解析:(1)=°=690°.
(2)-=-°=-390°.
答案:(1)690° (2)-390°
探究点2 用弧度制表示终边相同的角
把-1
480°写成2kπ+α(k∈Z)的形式,其中0≤α<2π,并判断它是第几象限角?
【解】 -1
480°=-1
480×=-=-10π+,其中0≤<2π,因为是第四象限角,
所以-1
480°是第四象限角.
(变问法)若本例的条件不变,在[-4π,4π)范围内找出与α终边相同的角的集合.
解:与α终边相同的角为2kπ+π(k∈Z).
由-4π≤2kπ+π<4π知
k=-2,-1,0,1.所以所求角的集合为
.
用弧度制表示终边相同角的两个关注点
(1)用弧度制表示终边相同的角2kπ+α(k∈Z)时,其中2kπ是π的偶数倍,而不是整数倍.
(2)注意角度制与弧度制不能混用.
1.若角θ的终边与角的终边相同,则在[0,2π]内终边与角的终边相同的角是____________.
解析:因为θ=+2kπ,k∈Z,所以=+,k∈Z.当k=0,1,2,3时,=,,,且∈[0,2π].
答案:,,,
2.如图所示:
(1)分别写出终边落在OA,OB位置上的角的集合;
(2)写出终边落在阴影部分(包括边界)的角的集合.
解:(1)终边在OA上的角的集合为
.
终边在OB上的角的集合为
.
(2).
探究点3 扇形的弧长与面积的计算
(1)已知扇形的圆心角为120°,半径为
cm,则此扇形的面积为________
cm2.
(2)已知扇形的周长为10
cm,面积为4
cm2,求扇形圆心角的弧度数.
【解】 (1)设扇形的弧长为l,
因为120°=120×
rad=(rad),
所以l=αR=×=(cm).
所以S=lR=××=π(cm2).故填π.
(2)设扇形圆心角的弧度数为θ(0<θ<2π),弧长为l,
半径为R,依题意有
①代入②得R2-5R+4=0,解得R1=1,R2=4.
当R=1时,l=8(cm),此时,θ=8
rad>2π
rad舍去.
当R=4时,l=2(cm),此时,
θ==
(rad).
综上可知,扇形圆心角的弧度数为
rad.
扇形的弧长和面积的求解策略
(1)记公式:弧度制下扇形的面积公式是S=lR=αR2(其中l是扇形的弧长,α是扇形圆心角的弧度数,0<α<2π).
(2)找关键:涉及扇形的半径、周长、弧长、圆心角、面积等计算问题,关键是分析题目中已知哪些量、求哪些量,然后灵活运用扇形弧长公式、面积公式直接求解或列方程(组)求解.
1.已知一个扇形的弧所对的圆心角为54°,半径r=20
cm,则该扇形的周长为________cm.
解析:因为1°=rad,所以54°=×54=,则扇形的弧长l=×20=6π(cm),故扇形的周长为(40+6π)cm.
答案:(40+6π)
2.已知一扇形的周长为40
cm,当它的半径和圆心角取什么值时,才能使扇形的面积最大?最大面积是多少?
解:设扇形的圆心角为θ,半径为r,弧长为l,面积为S,
则l+2r=40,
所以l=40-2r,
所以S=lr=×(40-2r)r=-(r-10)2+100.
所以当半径r=10
cm时,扇形的面积最大,最大值为100
cm2,这时θ===2
rad.
1.与60°终边相同的角可表示为( )
A.k·360°+(k∈Z)
B.2kπ+60°(k∈Z)
C.2k·360°+60°(k∈Z)
D.2kπ+(k∈Z)
解析:选D.选项A,B中角度的表示混合用到了角度制和弧度制,不符合要求;选项C错误,故选D.
2.(多选)下列转化结果正确的是( )
A.240°化成弧度是
B.-化成角度是-600°
C.-150°化成弧度是-
D.化成角度是15°
解析:选ABD.对于A,240°=240×=,正确;
对于B,-=-×°=-600°,正确;
对于C,-150°=-150×=-,错误;
对于D,=×°=15°,正确.
3.若角α的终边落在如图所示的阴影部分内,则角α的取值范围是( )
A.
B.
C.
D.(k∈Z)
解析:选D.阴影部分的两条边界分别是和角的终边,
所以α的取值范围是(k∈Z).
4.在半径为8
cm的圆中,的圆心角所对的弧长为________cm.
解析:根据弧长公式,得l=×8=
(cm).
答案:
5.把下列各角化成2kπ+α(0≤α<2π,k∈Z)的形式,并指出是第几象限角.
(1)-1
725°;(2).
解:(1)因为-1
725°=-5×360°+75°,
所以-1
725°=-10π+.
所以-1
725°角与角的终边相同.
又因为是第一象限角,所以-1
725°是第一象限角.
(2)因为=20π+,所以角与角的终边相同.
又因为是第三象限角,所以是第三象限角.
[A 基础达标]
1.对应的角度为( )
A.75°
B.125°
C.135°
D.155°
解析:选C.由于1
rad=°,
所以=π×°=135°,故选C.
2.用弧度制表示与150°角的终边相同的角的集合为( )
A.
B.
C.
D.
解析:选D.150°=150×=,故与150°角终边相同的角的集合为.
3.角的终边所在的象限是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
解析:选A.因为=2π+,角是第一象限角,所以角的终边所在的象限是第一象限.
4.钟表的分针在1点到3点20分这段时间里转过的弧度为( )
A.
π
B.-π
C.
π
D.-π
解析:选B.分针在1点到3点20分这段时间里,顺时针转过了周,转过的弧度为-×2π=-π.
5.如图,把八个等圆按相邻两两外切摆放,其圆心连线构成一个正八边形,设正八边形内侧八个扇形(无阴影部分)面积之和为S1,正八边形外侧八个扇形(阴影部分)面积之和为S2,则=( )
A.
B.
C.
D.1
解析:选B.因为正八边形的内角和为α1=(8-2)×180°=6×180°=1
080°=6π,
正八边形外侧八个扇形(阴影部分)的内角和为α2=360°×8-1
080°=2
880°-1
080°=1
800°=10π,
所以===.
6.用弧度制表示终边落在x轴上方的角α的集合为________.
解析:若角α的终边落在x轴上方,则2kπ<α<2kπ+π(k∈Z).
答案:{α|2kπ<α<2kπ+π,k∈Z}
7.(一题两空)在扇形中,已知半径为8,弧长为12,则圆心角α是________弧度,扇形面积S是________.
解析:|α|===rad,
S=lr=×12×8=48.
答案: 48
8.圆的半径变为原来的3倍,而所对弧长不变,则该弧所对圆心角是原来圆弧所对圆心角的____________.
解析:设原来圆的半径为r,弧长为l,弧所对的圆心角为α(0<α<2π),则现在的圆的半径为3r,弧长为l,设弧所对的圆心角为β(0<β<2π),于是l=αr=β·3r,所以β=α.
答案:
9.已知α=-800°.
(1)把α改写成β+2kπ(k∈Z,0≤β<2π)的形式,并指出α是第几象限角;
(2)求角γ,使γ与角α的终边相同,且γ∈.
解:(1)因为-800°=-3×360°+280°,280°=,
所以α=+(-3)×2π.
因为角α与终边相同,所以角α是第四象限角.
(2)因为与角α终边相同的角可写为2kπ+,k∈Z的形式,而γ与α终边相同,所以γ=2kπ+,k∈Z.
又γ∈,所以-<2kπ+<,k∈Z,
解得k=-1.所以γ=-2π+=-.
10.用弧度表示终边落在如图所示阴影部分内(不包括边界)的角θ的集合.
解:如题图(1),330°角的终边与-30°角的终边相同,
将-30°化为弧度,即-,而75°=75×=,
所以终边落在阴影部分内(不包括边界)的角的集合为
.
如题图(2),因为30°=,210°=,这两个角的终边所在的直线相同,
因此终边在直线AB上的角为α=kπ+,k∈Z,
又终边在y轴上的角为β=kπ+,k∈Z,
从而终边落在阴影部分内(不包括边界)的角的集合为
.
[B 能力提升]
11.若=2kπ+(k∈Z),则的终边在( )
A.第一象限
B.第四象限
C.x轴上
D.y轴上
解析:选D.因为=2kπ+(k∈Z),因为α=6kπ+π(k∈Z),所以=3kπ+(k∈Z).当k为奇数时,的终边在y轴的非正半轴上;当k为偶数时,的终边在y轴的非负半轴上.综上,的终边在y轴上,故选D.
12.(多选)扇形周长为6
cm,面积为2
cm2,则其圆心角的弧度数可能是( )
A.1
B.2
C.4
D.5
解析:选AC.设扇形的半径为r
cm,圆心角为α(0<α<2π),则
解得或故选AC.
13.(一题两空)已知圆的一段弧长等于该圆外切正三角形的边长,则这段弧所对圆心角的弧度数的绝对值为________;若圆弧长等于其所在圆的内接正方形的周长,那么这段弧所对圆心角的弧度数的绝对值为________.
解析:设圆的半径为r,这段弧所对圆心角的弧度数为θ,则圆外切正三角形的边长为2r,
所以|θ|==2;
又圆内接正方形的边长为r,圆弧长为4r,
所以|θ|==4.
答案:2 4
14.某企业欲做一个介绍企业发展史的铭牌,铭牌的截面形状是如图所示的扇形环面(由扇形OAD挖去扇形OBC后构成的).已知OA=10,OB=x(0m,设圆心角为θ弧度.
(1)求θ关于x的函数解析式;
(2)记铭牌的截面面积为y,试问x取何值时,y的值最大?并求出最大值.
解:(1)根据题意,可算得弧BC=xθ(m),弧AD=10θ(m).
因为BA+CD+l+l=30,
所以(10-x)+(10-x)+xθ+10θ=30,
所以θ=(0(2)根据题意,可知y=S扇形OAD-S扇形OBC=θ×102-θx2,
化简得y=-x2+5x+50=-+.
所以当x=(满足条件0综上所述,当x=m时铭牌的面积最大,
且最大面积为m2.
[C 拓展探究]
15.如图,一长为
dm,宽为1
dm的长方形木块在桌面上作无滑动翻滚,翻滚到第四次时被一小木块挡住,使木块底面与桌面所成角为,试求点A走过的路程及走过的弧所在的扇形的总面积.(圆心角为正)
解:在扇形ABA1中,圆心角恰为,弧长l1=·AB=·=π,面积S1=··AB2=··4=π.在扇形A1CA2中,圆心角也为,弧长l2=·A1C=·1=,面积S2=··A1C2=··12=.在扇形A2DA3中,圆心角为π--=,弧长l3=·A2D=·=π,面积S3=··A2D2=··()2=,所以点A走过的路程长l=l1+l2+l3=π++=,点A走过的弧所在的扇形的总面积S=S1+S2+S3=π++=.
HYPERLINK
"http://www.21cnjy.com/"
21世纪教育网(www.21cnjy.com)
教材考点
学习目标
核心素养
弧度制、角度制与弧度制的换算
了解弧度制的概念能进行角度与弧度之间的互化
数学抽象、数学运算
用弧度制表示终边相同的角
能用弧度制表示终边相同的角
数学运算
扇形的弧长与面积公式
理解弧度制下扇形的弧长与面积公式
数学运算
问题导学
预习教材P172-P175,并思考以下问题:
1.1弧度的角是如何定义的?
2.如何进行弧度与角度的换算?
3.以弧度为单位的扇形弧长、面积公式是什么?
1.度量角的两种制度
角度制
定义
用度作为单位来度量角的单位制
1度的角
1度的角等于周角的,记作1°
弧度制
定义
以弧度为单位来度量角的单位制
1弧度的角
长度等于半径长的圆弧所对的圆心角叫做1弧度的角.1弧度记作1
rad(rad可省略不写)
■微思考1
在大小不同的圆中,长度为1的弧所对的圆心角相等吗?
提示:不相等.这是因为长度为1的弧是指弧的长度为1,在大小不同的圆中,由于半径不同,所以圆心角也不同.
2.弧度数的计算与互化
(1)弧度数的计算
(2)弧度与角度的互化
■微思考2
(1)角度制、弧度制都是角的度量制,那么它们之间是如何换算的?
提示:换算公式为π=180°.
(2)你认为式子|α|=中,比值与所取的圆的半径大小是否有关?
提示:与半径大小无关,一定大小的圆心角α所对应的弧长与半径的比值是唯一确定的.
3.弧度制下扇形的弧长与面积公式(r是扇形所在圆的半径,n为扇形的圆心角)
公式 度量制
弧长公式
扇形面积公式
角度制
l=
S=
弧度制
l=|α|·r(0<|α|<2π)
S=lr=|α|r2(0<|α|<2π)
■微思考3
在应用扇形的面积公式S=|α|r2时,α的单位能是角度吗?
提示:不能,α的单位必须是弧度.
1.判断正误(正确的打“√”,错误的打“×”)
(1)1
rad的角比1°的角要大.( )
(2)用角度制和弧度制度量角,都与圆的半径有关.( )
(3)每个弧度制的角,都有唯一的角度制的角与之对应.( )
(4)1°的角是周角的,1
rad的角是周角的.( )
答案:(1)√ (2)× (3)√ (4)√
2.弧度化为角度是( )
A.278°
B.280°
C.288°
D.318°
答案:C
3.半径为2,圆心角为的扇形的面积是( )
A.
B.π
C.
D.
答案:C
4.(1)18°=________rad;(2)π=________.
答案:(1) (2)54°
探究点1 角度制与弧度制的互化
将下列角度与弧度进行互化:
(1)37°30′;(2)-216°;(3);(4)-.
【解】 (1)37°30′=37.5°=°=×=.
(2)-216°=-216×=-.
(3)=°=°=105°.
(4)-π=°=-396°.
角度制与弧度制的互化原则
(1)原则:牢记180°=π
rad,充分利用1°=
rad和1
rad=°进行换算.
(2)方法:设一个角的弧度数为α,角度数为n,则α
rad=°;n°=n·rad.
1.把下列角度化为弧度.
(1)-1
500°=________.
(2)67°30′=________.
解析:(1)-1
500°=-1
500×=-π.
(2)67°30′=67.5°=67.5×=.
答案:(1)- (2)
2.把下列弧度化为角度.
(1)=________.
(2)-=________.
解析:(1)=°=690°.
(2)-=-°=-390°.
答案:(1)690° (2)-390°
探究点2 用弧度制表示终边相同的角
把-1
480°写成2kπ+α(k∈Z)的形式,其中0≤α<2π,并判断它是第几象限角?
【解】 -1
480°=-1
480×=-=-10π+,其中0≤<2π,因为是第四象限角,
所以-1
480°是第四象限角.
(变问法)若本例的条件不变,在[-4π,4π)范围内找出与α终边相同的角的集合.
解:与α终边相同的角为2kπ+π(k∈Z).
由-4π≤2kπ+π<4π知
k=-2,-1,0,1.所以所求角的集合为
.
用弧度制表示终边相同角的两个关注点
(1)用弧度制表示终边相同的角2kπ+α(k∈Z)时,其中2kπ是π的偶数倍,而不是整数倍.
(2)注意角度制与弧度制不能混用.
1.若角θ的终边与角的终边相同,则在[0,2π]内终边与角的终边相同的角是____________.
解析:因为θ=+2kπ,k∈Z,所以=+,k∈Z.当k=0,1,2,3时,=,,,且∈[0,2π].
答案:,,,
2.如图所示:
(1)分别写出终边落在OA,OB位置上的角的集合;
(2)写出终边落在阴影部分(包括边界)的角的集合.
解:(1)终边在OA上的角的集合为
.
终边在OB上的角的集合为
.
(2).
探究点3 扇形的弧长与面积的计算
(1)已知扇形的圆心角为120°,半径为
cm,则此扇形的面积为________
cm2.
(2)已知扇形的周长为10
cm,面积为4
cm2,求扇形圆心角的弧度数.
【解】 (1)设扇形的弧长为l,
因为120°=120×
rad=(rad),
所以l=αR=×=(cm).
所以S=lR=××=π(cm2).故填π.
(2)设扇形圆心角的弧度数为θ(0<θ<2π),弧长为l,
半径为R,依题意有
①代入②得R2-5R+4=0,解得R1=1,R2=4.
当R=1时,l=8(cm),此时,θ=8
rad>2π
rad舍去.
当R=4时,l=2(cm),此时,
θ==
(rad).
综上可知,扇形圆心角的弧度数为
rad.
扇形的弧长和面积的求解策略
(1)记公式:弧度制下扇形的面积公式是S=lR=αR2(其中l是扇形的弧长,α是扇形圆心角的弧度数,0<α<2π).
(2)找关键:涉及扇形的半径、周长、弧长、圆心角、面积等计算问题,关键是分析题目中已知哪些量、求哪些量,然后灵活运用扇形弧长公式、面积公式直接求解或列方程(组)求解.
1.已知一个扇形的弧所对的圆心角为54°,半径r=20
cm,则该扇形的周长为________cm.
解析:因为1°=rad,所以54°=×54=,则扇形的弧长l=×20=6π(cm),故扇形的周长为(40+6π)cm.
答案:(40+6π)
2.已知一扇形的周长为40
cm,当它的半径和圆心角取什么值时,才能使扇形的面积最大?最大面积是多少?
解:设扇形的圆心角为θ,半径为r,弧长为l,面积为S,
则l+2r=40,
所以l=40-2r,
所以S=lr=×(40-2r)r=-(r-10)2+100.
所以当半径r=10
cm时,扇形的面积最大,最大值为100
cm2,这时θ===2
rad.
1.与60°终边相同的角可表示为( )
A.k·360°+(k∈Z)
B.2kπ+60°(k∈Z)
C.2k·360°+60°(k∈Z)
D.2kπ+(k∈Z)
解析:选D.选项A,B中角度的表示混合用到了角度制和弧度制,不符合要求;选项C错误,故选D.
2.(多选)下列转化结果正确的是( )
A.240°化成弧度是
B.-化成角度是-600°
C.-150°化成弧度是-
D.化成角度是15°
解析:选ABD.对于A,240°=240×=,正确;
对于B,-=-×°=-600°,正确;
对于C,-150°=-150×=-,错误;
对于D,=×°=15°,正确.
3.若角α的终边落在如图所示的阴影部分内,则角α的取值范围是( )
A.
B.
C.
D.(k∈Z)
解析:选D.阴影部分的两条边界分别是和角的终边,
所以α的取值范围是(k∈Z).
4.在半径为8
cm的圆中,的圆心角所对的弧长为________cm.
解析:根据弧长公式,得l=×8=
(cm).
答案:
5.把下列各角化成2kπ+α(0≤α<2π,k∈Z)的形式,并指出是第几象限角.
(1)-1
725°;(2).
解:(1)因为-1
725°=-5×360°+75°,
所以-1
725°=-10π+.
所以-1
725°角与角的终边相同.
又因为是第一象限角,所以-1
725°是第一象限角.
(2)因为=20π+,所以角与角的终边相同.
又因为是第三象限角,所以是第三象限角.
[A 基础达标]
1.对应的角度为( )
A.75°
B.125°
C.135°
D.155°
解析:选C.由于1
rad=°,
所以=π×°=135°,故选C.
2.用弧度制表示与150°角的终边相同的角的集合为( )
A.
B.
C.
D.
解析:选D.150°=150×=,故与150°角终边相同的角的集合为.
3.角的终边所在的象限是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
解析:选A.因为=2π+,角是第一象限角,所以角的终边所在的象限是第一象限.
4.钟表的分针在1点到3点20分这段时间里转过的弧度为( )
A.
π
B.-π
C.
π
D.-π
解析:选B.分针在1点到3点20分这段时间里,顺时针转过了周,转过的弧度为-×2π=-π.
5.如图,把八个等圆按相邻两两外切摆放,其圆心连线构成一个正八边形,设正八边形内侧八个扇形(无阴影部分)面积之和为S1,正八边形外侧八个扇形(阴影部分)面积之和为S2,则=( )
A.
B.
C.
D.1
解析:选B.因为正八边形的内角和为α1=(8-2)×180°=6×180°=1
080°=6π,
正八边形外侧八个扇形(阴影部分)的内角和为α2=360°×8-1
080°=2
880°-1
080°=1
800°=10π,
所以===.
6.用弧度制表示终边落在x轴上方的角α的集合为________.
解析:若角α的终边落在x轴上方,则2kπ<α<2kπ+π(k∈Z).
答案:{α|2kπ<α<2kπ+π,k∈Z}
7.(一题两空)在扇形中,已知半径为8,弧长为12,则圆心角α是________弧度,扇形面积S是________.
解析:|α|===rad,
S=lr=×12×8=48.
答案: 48
8.圆的半径变为原来的3倍,而所对弧长不变,则该弧所对圆心角是原来圆弧所对圆心角的____________.
解析:设原来圆的半径为r,弧长为l,弧所对的圆心角为α(0<α<2π),则现在的圆的半径为3r,弧长为l,设弧所对的圆心角为β(0<β<2π),于是l=αr=β·3r,所以β=α.
答案:
9.已知α=-800°.
(1)把α改写成β+2kπ(k∈Z,0≤β<2π)的形式,并指出α是第几象限角;
(2)求角γ,使γ与角α的终边相同,且γ∈.
解:(1)因为-800°=-3×360°+280°,280°=,
所以α=+(-3)×2π.
因为角α与终边相同,所以角α是第四象限角.
(2)因为与角α终边相同的角可写为2kπ+,k∈Z的形式,而γ与α终边相同,所以γ=2kπ+,k∈Z.
又γ∈,所以-<2kπ+<,k∈Z,
解得k=-1.所以γ=-2π+=-.
10.用弧度表示终边落在如图所示阴影部分内(不包括边界)的角θ的集合.
解:如题图(1),330°角的终边与-30°角的终边相同,
将-30°化为弧度,即-,而75°=75×=,
所以终边落在阴影部分内(不包括边界)的角的集合为
.
如题图(2),因为30°=,210°=,这两个角的终边所在的直线相同,
因此终边在直线AB上的角为α=kπ+,k∈Z,
又终边在y轴上的角为β=kπ+,k∈Z,
从而终边落在阴影部分内(不包括边界)的角的集合为
.
[B 能力提升]
11.若=2kπ+(k∈Z),则的终边在( )
A.第一象限
B.第四象限
C.x轴上
D.y轴上
解析:选D.因为=2kπ+(k∈Z),因为α=6kπ+π(k∈Z),所以=3kπ+(k∈Z).当k为奇数时,的终边在y轴的非正半轴上;当k为偶数时,的终边在y轴的非负半轴上.综上,的终边在y轴上,故选D.
12.(多选)扇形周长为6
cm,面积为2
cm2,则其圆心角的弧度数可能是( )
A.1
B.2
C.4
D.5
解析:选AC.设扇形的半径为r
cm,圆心角为α(0<α<2π),则
解得或故选AC.
13.(一题两空)已知圆的一段弧长等于该圆外切正三角形的边长,则这段弧所对圆心角的弧度数的绝对值为________;若圆弧长等于其所在圆的内接正方形的周长,那么这段弧所对圆心角的弧度数的绝对值为________.
解析:设圆的半径为r,这段弧所对圆心角的弧度数为θ,则圆外切正三角形的边长为2r,
所以|θ|==2;
又圆内接正方形的边长为r,圆弧长为4r,
所以|θ|==4.
答案:2 4
14.某企业欲做一个介绍企业发展史的铭牌,铭牌的截面形状是如图所示的扇形环面(由扇形OAD挖去扇形OBC后构成的).已知OA=10,OB=x(0
(1)求θ关于x的函数解析式;
(2)记铭牌的截面面积为y,试问x取何值时,y的值最大?并求出最大值.
解:(1)根据题意,可算得弧BC=xθ(m),弧AD=10θ(m).
因为BA+CD+l+l=30,
所以(10-x)+(10-x)+xθ+10θ=30,
所以θ=(0
化简得y=-x2+5x+50=-+.
所以当x=(满足条件0
且最大面积为m2.
[C 拓展探究]
15.如图,一长为
dm,宽为1
dm的长方形木块在桌面上作无滑动翻滚,翻滚到第四次时被一小木块挡住,使木块底面与桌面所成角为,试求点A走过的路程及走过的弧所在的扇形的总面积.(圆心角为正)
解:在扇形ABA1中,圆心角恰为,弧长l1=·AB=·=π,面积S1=··AB2=··4=π.在扇形A1CA2中,圆心角也为,弧长l2=·A1C=·1=,面积S2=··A1C2=··12=.在扇形A2DA3中,圆心角为π--=,弧长l3=·A2D=·=π,面积S3=··A2D2=··()2=,所以点A走过的路程长l=l1+l2+l3=π++=,点A走过的弧所在的扇形的总面积S=S1+S2+S3=π++=.
HYPERLINK
"http://www.21cnjy.com/"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
