1.5.3.1 【教案+测评】2019人教A版 必修 第一册 第五章 三角函数 第三节 诱导公式 第一课时 诱导公式二、三、四
文档属性
| 名称 | 1.5.3.1 【教案+测评】2019人教A版 必修 第一册 第五章 三角函数 第三节 诱导公式 第一课时 诱导公式二、三、四 |  | |
| 格式 | doc | ||
| 文件大小 | 871.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 20:49:31 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
教材考点
学习目标
核心素养
诱导公式二、三、四
理解诱导公式的推导方法
逻辑推理
诱导公式二、三、四的应用
能运用公式进行三角函数式的求值、化简以及证明
数学运算、逻辑推理
问题导学
预习教材P188-P190,并思考以下问题:
1.π±α,-α的终边与α的终边有怎样的对称关系?
2.诱导公式二、三、四的内容是什么?
1.公式二
终边关系
图示
角π+α与角α的终边关于原点对称
公式
sin(π+α)=-sin__α,cos(π+α)=-cos__α,tan(π+α)=tan__α
2.公式三
终边关系
图示
角-α与角α的终边关于x轴对称
公式
sin(-α)=-sin__α,cos(-α)=cos__α,tan(-α)=-tan
α
3.公式四
终边关系
图示
角π-α与角α的终边关于y轴对称
公式
sin(π-α)=sin__α,cos(π-α)=-cos__α,tan(π-α)=-tan__α
■微思考
这几组公式有什么统一的记忆方法吗?
提示:(1)记忆方法:2kπ+α,-α,π±α的三角函数值等于α的同名函数值,前面加上一个把α看成锐角时原函数值的符号.
(2)记忆口诀:“函数名不变,符号看象限”.
“口诀”的正确理解:“函数名不变”是指等式两边的三角函数同名;“符号”是指等号右边是正号还是负号;“看象限”是指假设α是锐角,要看原函数名在本公式中角的终边所在象限是取正值还是负值,如sin(π+α),若α看成锐角,则π+α在第三象限,正弦在第三象限取负值,故sin(π+α)=-sin
α.
1.判断正误(正确的打“√”,错误的打“×”)
(1)诱导公式三可以将任意负角的三角函数值转化为正角的三角函数值.( )
(2)对于诱导公式中的角α一定是锐角.( )
(3)由诱导公式三知cos[-(α-β)]=-cos(α-β).( )
(4)在△ABC中,sin(A+B)=sin
C.( )
答案:(1)√ (2)× (3)× (4)√
2.下列式子中正确的是( )
A.sin(π-α)=-sin
α
B.cos(π+α)=cos
α
C.cos
α=sin
α
D.sin(2π+α)=sin
α
答案:D
3.已知tan
α=6,则tan(π-α)=________.
答案:-6
4.cos
120°=________,sin=________.
答案:- -
探究点1 给角求值问题
利用公式求下列三角函数值:
(1)cos
π;(2)tan(-855°);
(3)sin(-945°)+cos(-π);
(4)tan
π+sin
π.
【解】 (1)cos
π=cos(π+6π)=cosπ=cos(2π-)=cos=.
(2)tan(-855°)=-tan
855°=-tan(2×360°+135°)=-tan
135°=-tan(180°-45°)=-tan(-45°)=tan
45°=1.
(3)原式=sin(-2×360°-225°)+cos
=sin(-225°)+cos
=-sin(180°+45°)+cos
=sin
45°-cos=-=.
(4)原式=tan(π-)+sin(2π-)
=-tan
-sin
=-1-
=-.
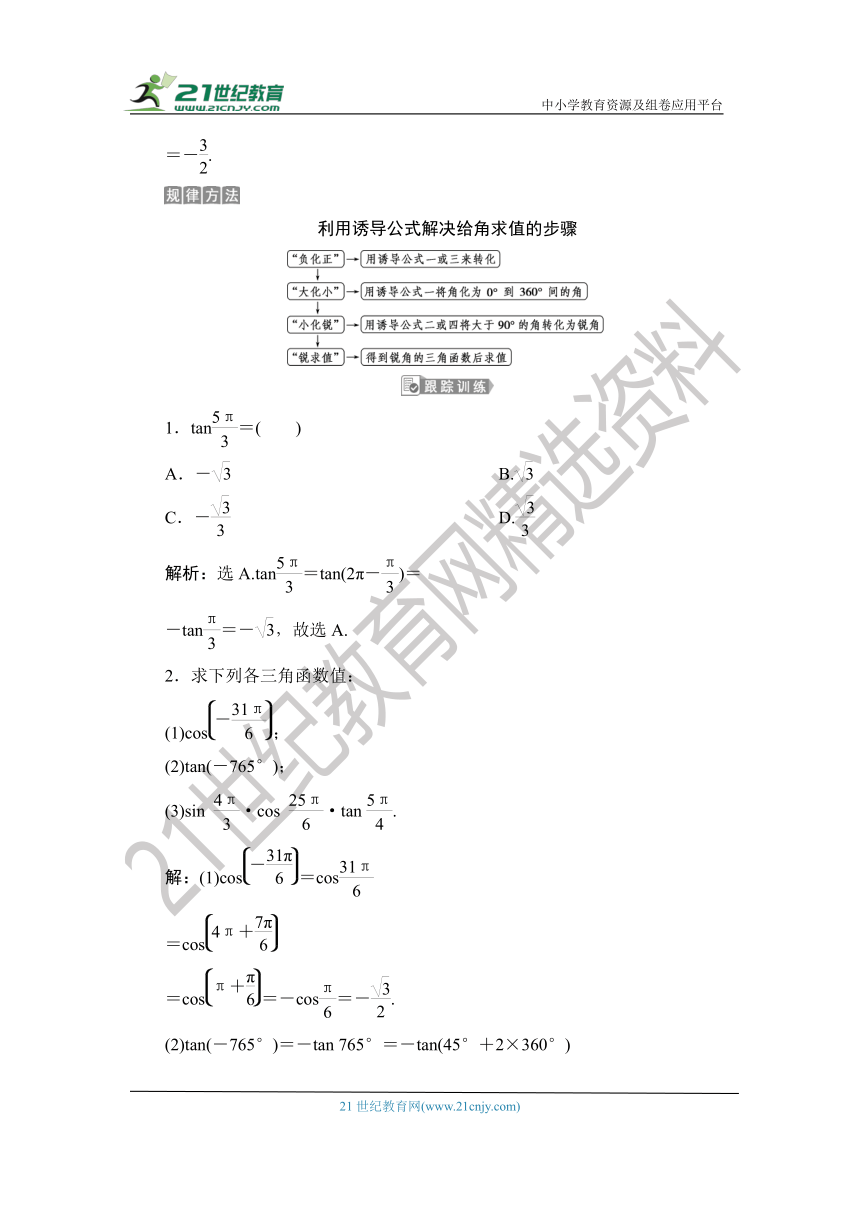
利用诱导公式解决给角求值的步骤
1.tan=( )
A.-
B.
C.-
D.
解析:选A.tan=tan(2π-)=
-tan=-,故选A.
2.求下列各三角函数值:
(1)cos;
(2)tan(-765°);
(3)sin
·cos
·tan
.
解:(1)cos=cos
=cos
=cos=-cos=-.
(2)tan(-765°)=-tan
765°=-tan(45°+2×360°)
=-tan
45°=-1.
(3)sin
·cos
·tan
=sincos·
tan
=-sin
cos
tan
=-××1=-.
探究点2 化简求值问题
化简下列各式.
(1);
(2).
【解】 (1)原式=
=
=-=-tan
α.
(2)原式=
===-1.
三角函数式化简的常用方法
(1)利用诱导公式,将任意角的三角函数转化为锐角三角函数.
(2)切化弦:一般需将表达式中的切函数转化为弦函数.
(3)注意“1”的应用:1=sin2α+cos2α=tan
.
1.化简:=________.
解析:=
===1.
答案:1
2.化简=________.
解析:原式=
==1.
答案:1
探究点3 给值(式)求值问题
(1)若cos(2π-α)=且α∈,则sin(π-α)=( )
A.-
B.-
C.-
D.±
(2)已知cos=,则cos=________.
【解析】 (1)因为cos(2π-α)=cos
α=,
且α∈,所以sin
α=-=-,
所以sin(π-α)=sin
α=-.
(2)cos=cos
=-cos=-.
【答案】 (1)B (2)-
1.(变问法)若本例(2)中的条件不变,求cos.
解:cos=cos=cos
=cos=.
2.(变问法)若本例(2)中的条件不变,求cos-sin2的值.
解:因为cos=cos
=-cos=-,
sin2=sin2=1-cos2=1-=,
所以cos-sin2=--=-.
解决条件求值问题的策略
(1)解决条件求值问题,首先要仔细观察条件与所求式之间的角、函数名称及有关运算之间的差异及联系.
(2)可以将已知式进行变形向所求式转化,或将所求式进行变形向已知式转化.
1.若sin(π+α)=,α∈,则tan(π-α)等于( )
A.-
B.-
C.-
D.-
解析:选D.因为sin(π+α)=-sin
α,
根据条件得sin
α=-,又α∈,
所以cos
α=-=-.
所以tan
α===.
所以tan(π-α)=-tan
α=-.
2.已知tan(π+α)=3,求的值.
解:因为tan(π+α)=3,
所以tan
α=3.
故
=
===7.
1.计算cos(-600°)=( )
A.
B.-
C.
D.-
解析:选D.cos(-600°)=cos
600°=cos(360°+240°)=cos
240°=cos(180°+60°)=-cos
60°=-.
2.已知cos(α-π)=-,且α是第四象限角,则sin(-2π+α)等于( )
A.-
B.
C.±
D.
解析:选A.由cos(α-π)=-,得cos
α=.又α为第四象限角,所以sin(-2π+α)=sin
α=-=-.
3.计算tan
690°=________.
解析:tan
690°=tan(2×360°-30°)=tan(-30°)
=-tan
30°=-.
答案:-
4.可化简为________.
解析:
==
=|1-sin
θ|=1-sin
θ.
答案:1-sin
θ
5.化简:.
解:原式=
=
==-cos2α.
[A 基础达标]
1.cos的值为( )
A.-
B.-
C.
D.
解析:选C.cos=cos(2π-)=cos(-)=cos=.
2.已知角α和β的终边关于x轴对称,则下列各式中正确的是( )
A.sin
α=sin
β
B.sin(α-2π)=sin
β
C.cos
α=cos
β
D.cos(2π-α)=-cos
β
解析:选C.由角α和β的终边关于x轴对称,可知β=-α+2kπ(k∈Z),故cos
α=cos
β.
3.sin
600°+tan(-300°)的值是( )
A.-
B.
C.-+
D.+
解析:选B.原式=sin(360°+180°+60°)+tan(-360°+60°)=-sin
60°+tan
60°=.
4.若sin(π+α)+sin(-α)=-m,则sin(3π+α)+2sin(2π-α)等于( )
A.-m
B.-m
C.m
D.m
解析:选B.因为sin(π+α)+sin(-α)=-2sin
α=-m,
所以sin
α=,则sin(3π+α)+2sin(2π-α)=-sin
α-2sin
α=-3sin
α=-m.故选B.
5.设f(α)=,则f的值为( )
A.
B.-
C.
D.-
解析:选D.f(α)=
==-.
所以f=-=-=-.
6.sin=________.
解析:sin=-sin
=-sin=sin
=sin=-sin
=-.
答案:-
7.化简:·tan(2π-α)=________.
解析:原式=·tan(-α)
=·=-1.
答案:-1
8.当θ=时,(k∈Z)的值等于________.
解析:原式==-.
当θ=时,原式=-=2.
答案:2
9.已知sin(α-π)=2cos(2π-α),求证:
=-.
证明:因为sin(α-π)=2cos(2π-α),
所以-sin
α=2cos
α,所以sin
α=-2cos
α.
所以左边=
===-=右边,
所以原式得证.
10.求值:sin(-1
200°)×cos
1
290°+cos(-1
020°)×sin(-1
050°)+tan
855°.
解:原式=-sin(120°+3×360°)×cos(210°+3×360°)+cos(300°+2×360°)×[-sin(330°+2×360°)]+tan(135°+2×360°)
=-sin
120°×cos
210°-cos
300°×sin
330°+tan
135°
=-sin
(180°-60°)×cos
(180°+30°)-cos(360°-60°)×sin(360°-30°)+tan(180°-45°)
=sin
60°×cos
30°+cos
60°×sin
30°-tan
45°
=×+×-1
=0.
[B 能力提升]
11.已知tan=,则tan=( )
A.
B.-
C.
D.-
解析:选B.因为tan=tan=-tan,
所以tan=-.
12.(多选)定义:角θ与φ都是任意角,若满足θ+φ=,则称θ与φ“广义互余”.已知sin(π+α)=-,下列角β中,可能与角α“广义互余”的是( )
A.sin
β=
B.cos(π+β)=
C.tan
β=
D.cos(2π-β)=
解析:选ACD.因为sin(π+α)=-sin
α=-,
所以sin
α=,
若α+β=,则β=-α.
A中sin
β=sin=cos
α=±,故A符合条件;
B中,cos(π+β)=-cos=-sin
α=-,故B不符合条件;
C中,tan
β=,即sin
β=cos
β,
又sin2β+cos2
β=1,故sin
β=±,即C符合条件;
D中,cos(2π-β)=cos
β=,
所以sin
β=±,故D符合条件.故选ACD.
13.(一题两空)已知sin(α+π)=,且sin
αcos
α<0,
则
(1)tan
α=________;
(2)=________.
解析:(1)因为sin(α+π)=,
所以sin
α=-,
又因为sin
αcos
α<0,
所以cos
α>0,cos
α==,
所以tan
α=-.
(2)原式=
==-.
答案:(1)- (2)-
14.已知f(n)=sin(n∈Z),
求f(1)+f(2)+f(3)+…+f(2
020)的值.
解:f(1)=sin=,f(2)=sin=,f(3)=sin
π=0,f(4)=sin=-,f(5)=sin=-,f(6)=sin
2π=0,f(7)=sin=sin
=f(1),f(8)=f(2),…,
因为f(1)+f(2)+f(3)+…+f(6)=0,所以f(1)+f(2)+f(3)+…+f(2
020)=f(1)+f(2)+f(3)+f(4)+336×0=.
[C 拓展探究]
15.化简下列各式.
(1)(k∈Z);
(2).
解:(1)当k=2n(n∈Z)时,
原式=
=
==-1;
当k=2n+1(n∈Z)时,
原式=
===-1.
综上,原式=-1.
(2)原式=
=
=
==-1.
HYPERLINK
"http://www.21cnjy.com/"
21世纪教育网(www.21cnjy.com)
教材考点
学习目标
核心素养
诱导公式二、三、四
理解诱导公式的推导方法
逻辑推理
诱导公式二、三、四的应用
能运用公式进行三角函数式的求值、化简以及证明
数学运算、逻辑推理
问题导学
预习教材P188-P190,并思考以下问题:
1.π±α,-α的终边与α的终边有怎样的对称关系?
2.诱导公式二、三、四的内容是什么?
1.公式二
终边关系
图示
角π+α与角α的终边关于原点对称
公式
sin(π+α)=-sin__α,cos(π+α)=-cos__α,tan(π+α)=tan__α
2.公式三
终边关系
图示
角-α与角α的终边关于x轴对称
公式
sin(-α)=-sin__α,cos(-α)=cos__α,tan(-α)=-tan
α
3.公式四
终边关系
图示
角π-α与角α的终边关于y轴对称
公式
sin(π-α)=sin__α,cos(π-α)=-cos__α,tan(π-α)=-tan__α
■微思考
这几组公式有什么统一的记忆方法吗?
提示:(1)记忆方法:2kπ+α,-α,π±α的三角函数值等于α的同名函数值,前面加上一个把α看成锐角时原函数值的符号.
(2)记忆口诀:“函数名不变,符号看象限”.
“口诀”的正确理解:“函数名不变”是指等式两边的三角函数同名;“符号”是指等号右边是正号还是负号;“看象限”是指假设α是锐角,要看原函数名在本公式中角的终边所在象限是取正值还是负值,如sin(π+α),若α看成锐角,则π+α在第三象限,正弦在第三象限取负值,故sin(π+α)=-sin
α.
1.判断正误(正确的打“√”,错误的打“×”)
(1)诱导公式三可以将任意负角的三角函数值转化为正角的三角函数值.( )
(2)对于诱导公式中的角α一定是锐角.( )
(3)由诱导公式三知cos[-(α-β)]=-cos(α-β).( )
(4)在△ABC中,sin(A+B)=sin
C.( )
答案:(1)√ (2)× (3)× (4)√
2.下列式子中正确的是( )
A.sin(π-α)=-sin
α
B.cos(π+α)=cos
α
C.cos
α=sin
α
D.sin(2π+α)=sin
α
答案:D
3.已知tan
α=6,则tan(π-α)=________.
答案:-6
4.cos
120°=________,sin=________.
答案:- -
探究点1 给角求值问题
利用公式求下列三角函数值:
(1)cos
π;(2)tan(-855°);
(3)sin(-945°)+cos(-π);
(4)tan
π+sin
π.
【解】 (1)cos
π=cos(π+6π)=cosπ=cos(2π-)=cos=.
(2)tan(-855°)=-tan
855°=-tan(2×360°+135°)=-tan
135°=-tan(180°-45°)=-tan(-45°)=tan
45°=1.
(3)原式=sin(-2×360°-225°)+cos
=sin(-225°)+cos
=-sin(180°+45°)+cos
=sin
45°-cos=-=.
(4)原式=tan(π-)+sin(2π-)
=-tan
-sin
=-1-
=-.
利用诱导公式解决给角求值的步骤
1.tan=( )
A.-
B.
C.-
D.
解析:选A.tan=tan(2π-)=
-tan=-,故选A.
2.求下列各三角函数值:
(1)cos;
(2)tan(-765°);
(3)sin
·cos
·tan
.
解:(1)cos=cos
=cos
=cos=-cos=-.
(2)tan(-765°)=-tan
765°=-tan(45°+2×360°)
=-tan
45°=-1.
(3)sin
·cos
·tan
=sincos·
tan
=-sin
cos
tan
=-××1=-.
探究点2 化简求值问题
化简下列各式.
(1);
(2).
【解】 (1)原式=
=
=-=-tan
α.
(2)原式=
===-1.
三角函数式化简的常用方法
(1)利用诱导公式,将任意角的三角函数转化为锐角三角函数.
(2)切化弦:一般需将表达式中的切函数转化为弦函数.
(3)注意“1”的应用:1=sin2α+cos2α=tan
.
1.化简:=________.
解析:=
===1.
答案:1
2.化简=________.
解析:原式=
==1.
答案:1
探究点3 给值(式)求值问题
(1)若cos(2π-α)=且α∈,则sin(π-α)=( )
A.-
B.-
C.-
D.±
(2)已知cos=,则cos=________.
【解析】 (1)因为cos(2π-α)=cos
α=,
且α∈,所以sin
α=-=-,
所以sin(π-α)=sin
α=-.
(2)cos=cos
=-cos=-.
【答案】 (1)B (2)-
1.(变问法)若本例(2)中的条件不变,求cos.
解:cos=cos=cos
=cos=.
2.(变问法)若本例(2)中的条件不变,求cos-sin2的值.
解:因为cos=cos
=-cos=-,
sin2=sin2=1-cos2=1-=,
所以cos-sin2=--=-.
解决条件求值问题的策略
(1)解决条件求值问题,首先要仔细观察条件与所求式之间的角、函数名称及有关运算之间的差异及联系.
(2)可以将已知式进行变形向所求式转化,或将所求式进行变形向已知式转化.
1.若sin(π+α)=,α∈,则tan(π-α)等于( )
A.-
B.-
C.-
D.-
解析:选D.因为sin(π+α)=-sin
α,
根据条件得sin
α=-,又α∈,
所以cos
α=-=-.
所以tan
α===.
所以tan(π-α)=-tan
α=-.
2.已知tan(π+α)=3,求的值.
解:因为tan(π+α)=3,
所以tan
α=3.
故
=
===7.
1.计算cos(-600°)=( )
A.
B.-
C.
D.-
解析:选D.cos(-600°)=cos
600°=cos(360°+240°)=cos
240°=cos(180°+60°)=-cos
60°=-.
2.已知cos(α-π)=-,且α是第四象限角,则sin(-2π+α)等于( )
A.-
B.
C.±
D.
解析:选A.由cos(α-π)=-,得cos
α=.又α为第四象限角,所以sin(-2π+α)=sin
α=-=-.
3.计算tan
690°=________.
解析:tan
690°=tan(2×360°-30°)=tan(-30°)
=-tan
30°=-.
答案:-
4.可化简为________.
解析:
==
=|1-sin
θ|=1-sin
θ.
答案:1-sin
θ
5.化简:.
解:原式=
=
==-cos2α.
[A 基础达标]
1.cos的值为( )
A.-
B.-
C.
D.
解析:选C.cos=cos(2π-)=cos(-)=cos=.
2.已知角α和β的终边关于x轴对称,则下列各式中正确的是( )
A.sin
α=sin
β
B.sin(α-2π)=sin
β
C.cos
α=cos
β
D.cos(2π-α)=-cos
β
解析:选C.由角α和β的终边关于x轴对称,可知β=-α+2kπ(k∈Z),故cos
α=cos
β.
3.sin
600°+tan(-300°)的值是( )
A.-
B.
C.-+
D.+
解析:选B.原式=sin(360°+180°+60°)+tan(-360°+60°)=-sin
60°+tan
60°=.
4.若sin(π+α)+sin(-α)=-m,则sin(3π+α)+2sin(2π-α)等于( )
A.-m
B.-m
C.m
D.m
解析:选B.因为sin(π+α)+sin(-α)=-2sin
α=-m,
所以sin
α=,则sin(3π+α)+2sin(2π-α)=-sin
α-2sin
α=-3sin
α=-m.故选B.
5.设f(α)=,则f的值为( )
A.
B.-
C.
D.-
解析:选D.f(α)=
==-.
所以f=-=-=-.
6.sin=________.
解析:sin=-sin
=-sin=sin
=sin=-sin
=-.
答案:-
7.化简:·tan(2π-α)=________.
解析:原式=·tan(-α)
=·=-1.
答案:-1
8.当θ=时,(k∈Z)的值等于________.
解析:原式==-.
当θ=时,原式=-=2.
答案:2
9.已知sin(α-π)=2cos(2π-α),求证:
=-.
证明:因为sin(α-π)=2cos(2π-α),
所以-sin
α=2cos
α,所以sin
α=-2cos
α.
所以左边=
===-=右边,
所以原式得证.
10.求值:sin(-1
200°)×cos
1
290°+cos(-1
020°)×sin(-1
050°)+tan
855°.
解:原式=-sin(120°+3×360°)×cos(210°+3×360°)+cos(300°+2×360°)×[-sin(330°+2×360°)]+tan(135°+2×360°)
=-sin
120°×cos
210°-cos
300°×sin
330°+tan
135°
=-sin
(180°-60°)×cos
(180°+30°)-cos(360°-60°)×sin(360°-30°)+tan(180°-45°)
=sin
60°×cos
30°+cos
60°×sin
30°-tan
45°
=×+×-1
=0.
[B 能力提升]
11.已知tan=,则tan=( )
A.
B.-
C.
D.-
解析:选B.因为tan=tan=-tan,
所以tan=-.
12.(多选)定义:角θ与φ都是任意角,若满足θ+φ=,则称θ与φ“广义互余”.已知sin(π+α)=-,下列角β中,可能与角α“广义互余”的是( )
A.sin
β=
B.cos(π+β)=
C.tan
β=
D.cos(2π-β)=
解析:选ACD.因为sin(π+α)=-sin
α=-,
所以sin
α=,
若α+β=,则β=-α.
A中sin
β=sin=cos
α=±,故A符合条件;
B中,cos(π+β)=-cos=-sin
α=-,故B不符合条件;
C中,tan
β=,即sin
β=cos
β,
又sin2β+cos2
β=1,故sin
β=±,即C符合条件;
D中,cos(2π-β)=cos
β=,
所以sin
β=±,故D符合条件.故选ACD.
13.(一题两空)已知sin(α+π)=,且sin
αcos
α<0,
则
(1)tan
α=________;
(2)=________.
解析:(1)因为sin(α+π)=,
所以sin
α=-,
又因为sin
αcos
α<0,
所以cos
α>0,cos
α==,
所以tan
α=-.
(2)原式=
==-.
答案:(1)- (2)-
14.已知f(n)=sin(n∈Z),
求f(1)+f(2)+f(3)+…+f(2
020)的值.
解:f(1)=sin=,f(2)=sin=,f(3)=sin
π=0,f(4)=sin=-,f(5)=sin=-,f(6)=sin
2π=0,f(7)=sin=sin
=f(1),f(8)=f(2),…,
因为f(1)+f(2)+f(3)+…+f(6)=0,所以f(1)+f(2)+f(3)+…+f(2
020)=f(1)+f(2)+f(3)+f(4)+336×0=.
[C 拓展探究]
15.化简下列各式.
(1)(k∈Z);
(2).
解:(1)当k=2n(n∈Z)时,
原式=
=
==-1;
当k=2n+1(n∈Z)时,
原式=
===-1.
综上,原式=-1.
(2)原式=
=
=
==-1.
HYPERLINK
"http://www.21cnjy.com/"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
