1.1.1.1 【教案+测评】2019人教A版 必修 第一册 第一章 集合与常用逻辑用语 第一节 集合的概念 第一课时 集合的概念
文档属性
| 名称 | 1.1.1.1 【教案+测评】2019人教A版 必修 第一册 第一章 集合与常用逻辑用语 第一节 集合的概念 第一课时 集合的概念 |

|
|
| 格式 | doc | ||
| 文件大小 | 567.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 21:00:58 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
教材考点
学习目标
核心素养
集合的概念
了解集合与元素的概念
数学抽象
元素与集合的关系
理解元素与集合的关系,掌握数学中一些常见的数集及其记法
数学抽象、逻辑推理
集合中元素的特性及应用
理解集合中元素的特性,并能利用它们进行解题
数学运算、数学抽象
INCLUDEPICTURE"温馨提示ALLL.TIF"问题导学
预习教材P2-P3,并思考以下问题:
1.集合和元素的概念是什么?
2.如何用字母表示集合和元素?
3.元素和集合之间有哪两种关系?
4.常见的数集有哪些?分别用什么符号表示?
INCLUDEPICTURE"新知初探LLL.TIF"
1.元素与集合的概念
(1)元素:一般地,我们把研究对象统称为元素.元素通常用小写拉丁字母a,b,c,…表示.
(2)集合:把一些元素组成的总体叫做集合(简称为集).集合通常用大写拉丁字母A,B,C,…表示.
(3)集合相等:只要构成两个集合的元素是一样的,我们就称这两个集合是相等的.
(4)元素的特性:确定性、无序性、互异性.
■微思考1
(1)集合中的元素只能是数学中的数、点、代数式吗?
提示:集合中的元素所指的范围非常广泛,可以是数学中的数、点、代数式,也可以是现实生活中的各种各样的事物或人等.
(2)“很瘦的人”能构成集合吗?为什么?
提示:“很瘦的人”不能构成集合.因为它没有确定的标准.如果给定一个集合A,一个研究对象a是不是这个集合中的元素就确定了.
2.元素与集合的关系
关系
语言描述
记法
读法
属于
a是集合A中的元素
a∈A
a属于集合A
不属于
a不是集合A中的元素
a?A
a不属于集合A
■微思考2
(1)元素与集合之间有第三种关系吗?
提示:对于一个元素a与一个集合A而言,只有“a∈A”与“a?A”这两种结果.
(2)符号“∈”“?”的左边可以是集合吗?
提示:∈和?具有方向性,左边是元素,右边是集合,形如R∈0是错误的.
3.常用的数集及其记法
常用的数集
自然数集
正整数集
整数集
有理数集
实数集
记法
N
N
或N+
Z
Q
R
■微思考3
N与N+(或N
)有何区别?
提示:N+是所有正整数组成的集合,而N是由0和所有的正整数组成的集合,所以N比N+(或N
)多一个元素0.
INCLUDEPICTURE"自我检测LLL.TIF"
INCLUDEPICTURE
"../../../../自我检测LLL.TIF"
\
MERGEFORMAT
1.判断正误(正确的打“√”,错误的打“×”)
(1)集合中的元素一定是数.( )
(2)由1,2,3构成的集合与由3,2,1构成的集合是同一个集合. ( )
(3)一个集合中可以找到两个相同的元素.( )
(4)集合N中的最小元素为0.( )
(5)若a∈Q,则一定有a∈R.( )
答案:(1)× (2)√ (3)× (4)√ (5)√
2.由“title”中的字母构成的集合中元素的个数为( )
A.2
B.3
C.4
D.5
解析:选C.由“title”中的字母构成的集合中元素为t,i,l,e,共4个.
3.下列关系①0.21∈Q;②?N
;③-∈N
;④∈N.其中正确的个数是( )
A.0
B.1
C.2
D.3
解析:选C.①是正确的,②中=2∈N
,③中-=-2?N
,④=2∈N是正确的,故①④正确.
4.已知集合M有两个元素3和a+1,且4∈M,则实数a=________.
解析:由题意知a+1=4,即a=3.
答案:3
INCLUDEPICTURE"探究案讲练互动LLL.TIF"
探究点1 集合的概念
INCLUDEPICTURE"例1LLL.TIF"
INCLUDEPICTURE
"../../../../例1LLL.TIF"
\
MERGEFORMAT
2020年9月,我们踏入了心仪的高中校园,找到了自己的班级.则下列对象中能构成一个集合的是哪些?并说明你的理由.
(1)你所在班级中的全体同学;
(2)班级中比较高的同学;
(3)班级中身高超过178
cm的同学;
(4)班级中比较胖的同学;
(5)班级中体重超过75
kg的同学;
(6)学习成绩比较好的同学
【解】 (1)班级中的全体同学是确定的,所以可以构成一个集合.
(2)因为“比较高”无法衡量,所以对象不确定,所以不能构成一个集合.
(3)因为“身高超过178
cm”是确定的,所以可以构成一个集合.
(4)“比较胖”无法衡量,所以对象不确定,所以不能构成一个集合.
(5)“体重超过75
kg”是确定的,所以可以构成一个集合.
(6)“学习成绩比较好”无法衡量,所以对象不确定,所以不能构成一个集合.
判断一组对象能否构成集合的方法
一般地,确认一组对象a1,a2,a3,…,an(a1,a2,…,an均不相同)能否构成集合的过程为:
INCLUDEPICTURE
"../../../../ab4.TIF"
\
MERGEFORMAT
INCLUDEPICTURE"跟踪训练LLL.TIF"
1.(多选)下列各组对象能构成集合的是( )
A.拥有手机的人
B.2020年高考数学难题
C.所有有理数
D.小于π的正整数
解析:选ACD.B选项中“难题”的标准不明确,不符合确定性,显然A,C,D选项中能构成集合,故选ACD.
2.中国男子篮球职业联赛(China
Basketball
Association),简称中职篮(CBA),是由中国篮球协会所主办的跨年度主客场制篮球联赛,是中国最高等级的篮球联赛.下列对象能构成一个集合的是________(填序号).
①2019~2020赛季,CBA的所有队伍;
②CBA中比较著名的队员;
③CBA中得分前五位的球员;
④CBA中比较高的球员.
解析:①CBA的所有队伍是确定的,所以可以构成一个集合.
②“比较著名”没有衡量的标准,对象不确定,所以不能构成一个集合.
③“得分前五位”是确定的,所以可以构成一个集合.
④“比较高”没有衡量的标准,对象不确定,所以不能构成一个集合.
答案:①③
探究点2 元素与集合的关系
(1)集合M是由大于-2且小于1的实数构成的,则下列关系式正确的是( )
A.∈M
B.0?M
C.1∈M
D.-∈M
(2)用符号∈和?填空.
①设集合A是正整数的集合,则0________A,________A,(-1)0________A;
②设集合D是由满足y=x2的有序实数对(x,y)组成的,则-1________D,(-1,1)________D;
③设集合M由可表示为a+b(a∈Z,b∈Z)的实数构成,则0________M,________M,________M.
【解析】 (1)>1,故?M;-2<0<1,故0∈M;1不小于1,故1?M;-2<-<1,故-∈M.故选D.
(2)①0不是正整数,不是正整数,(-1)0=1是正整数;②-1不是有序实数对,所以-1?D,(-1,1)满足y=x2,故(-1,1)∈D;③因为0=0+0×,所以0∈M,因为=1+1×,所以∈M,因为=+1×,?Z,所以?M.
【答案】 (1)D (2)①? ? ∈ ②? ∈ ③∈ ∈ ?
判断元素和集合关系的两种方法
(1)直接法:如果集合中的元素是直接给出的,只要判断该元素在已知集合中是否给出即可.
此时应首先明确集合是由哪些元素构成的.
(2)推理法:对于某些不便直接表示的集合,判断元素与集合的关系时,只要判断该元素是否满足集合中元素所具有的特征即可.此时应首先明确已知集合的元素具有什么属性,即该集合中元素要符合哪种表达式或满足哪些条件.
1.下列关系中,正确的有( )
①∈R;②?Q;③|-3|∈N;④|-|∈Q.
A.1个
B.2个
C.3个
D.4个
解析:选C.是实数,是无理数,|-3|=3是非负整数,|-|=是无理数.
因此①②③正确,④错误.
2.已知集合A中元素满足2x+a>0,a∈R.若1?A,2∈A,则实数a的取值范围为________.
解析:因为1?A,2∈A,
所以
即-4答案:-4探究点3 集合中元素的特征及应用
INCLUDEPICTURE"例3LLL.TIF"
已知集合A中含有两个元素a和a2,若1∈A,则实数a的值为________.
【解析】 若1∈A,则a=1或a2=1,
即a=±1.
当a=1时,集合A中有重复元素,
所以a≠1;
当a=-1时,集合A含有两个元素1,-1,符合元素的互异性,所以a=-1.
【答案】 -1
1.(变条件)若去掉本例中的条件“1∈A”,则实数a的取值范围是什么?
解:因为集合A中含有两个元素a和a2,
所以a≠a2,
即a≠0且a≠1.
2.(变条件)若将本例中的“1∈A”改为“2∈A”,则a为何值?
解:因为2∈A,
所以a=2或a2=2,
即a=2或a=±.
3.(变条件)若由a和a2构成的集合只有一个元素,则a为何值?
解:因为由a和a2构成的集合只有一个元素,所以a=a2,即a=0或a=1.
由集合中元素的特征求解字母取值(范围)的步骤
INCLUDEPICTURE
"../../../../MF1.TIF"
\
MERGEFORMAT
INCLUDEPICTURE"跟踪训练LLL.TIF"
1.若集合M中的三个元素是△ABC的三边长,则△ABC一定不是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形
解析:选D.由集合中元素的互异性可知,集合中的任何两个元素都不相同,故选D.
2.若集合A中有三个元素x,x+1,1,集合B中也有三个元素x,x+x2,x2,且A=B,求实数x的值.
解:因为A=B,
所以或
解得x=±1.经检验,x=1不适合集合元素的互异性,而x=-1适合,
所以x=-1.
INCLUDEPICTURE"自测案当堂达标LLL.TIF"
1.考察下列每组对象,能组成一个集合的是( )
①一中高一年级聪明的学生;②直角坐标系中横、纵坐标相等的点;③不小于3的正整数;④的近似值.
A.①②
B.③④
C.②③
D.①③
解析:选C.①“一中高一年级聪明的学生”的标准不确定,因而不能构成集合;②“直角坐标系中横、纵坐标相等的点”的标准确定,能构成集合;③“不小于3的正整数”的标准确定,能构成集合;④“的近似值”的标准不确定,不能构成集合.
2.下列结论中,不正确的是( )
A.若a∈N,则?N
B.若a∈Z,则a2∈Z
C.若a∈Q,则|a|∈Q
D.若a∈R,则∈R
解析:选A.A不正确.反例a=1∈N,=1∈N.
3.若以方程x2-5x+6=0和x2-x-2=0的解为元素组成集合M,则M中元素的个数为( )
A.1
B.2
C.3
D.4
解析:选C.方程x2-5x+6=0的解为x=2或x=3,x2-x-2=0的解为x=2或x=-1,所以集合M中含有3个元素.
4.用适当的符号填空:
已知集合A中的元素x是被3除余2的整数,则有:
17________A;-5________A.
解析:由题意可设x=3k+2,k∈Z,
令3k+2=17得,k=5∈Z
.
所以17∈A.令3k+2=-5得,
k=-?Z.所以-5?A.
答案:∈ ?
5.已知集合A是由0,m,m2-3m+2三个元素构成的集合,且2∈A,则实数m=________.
解析:由题意知,m=2或m2-3m+2=2,
解得m=2或m=0或m=3,经验证,
当m=0或m=2时,
不满足集合中元素的互异性,
当m=3时,满足题意,
故m=3.
答案:3INCLUDEPICTURE"应用案巩固提升LLL.TIF"
[A 基础达标]
1.有以下说法,其中正确的是( )
①接近于0的数的全体构成一个集合;
②正方体的全体构成一个集合;
③未来世界的高科技产品构成一个集合;
④不大于3的所有自然数构成一个集合.
A.①②
B.②③
C.③④
D.②④
解析:选D.在①中,接近于0的数的全体不能构成一个集合,故①错误;在②中,正方体的全体能构成一个集合,故②正确;在③中,未来世界的高科技产品不能构成一个集合,故③错误;在④中,不大于3的所有自然数能构成一个集合,故④正确.
2.给出下列关系:①∈R;②∈Q;③-3?Z;④-?N,其中正确的个数为( )
A.1
B.2
C.3
D.4
解析:选B.是实数,①正确;是无理数,②错误;-3是整数,③错误;-是无理数,④正确.故选B.
3.设A是方程2x2+ax+2=0的解集,且2∈A,则实数a的值为( )
A.-5
B.-4
C.4
D.5
解析:选A.因为2∈A,
所以2×22+2a+2=0,
解得a=-5.
4.设集合M是由不小于2的数组成的集合,a=,则下列关系中正确的是( )
A.a∈M
B.a?M
C.a=M
D.a≠M
解析:选B.因为集合M是由不小于2的数组成的集合,a=,所以a不是集合M中的元素,故a?M.
5.由实数x,-x,|x|,,-所组成的集合,最多含有( )
A.2个元素
B.3个元素
C.4个元素
D.5个元素
解析:选A.=|x|,-=-x.
当x=0时,它们均为0;
当x>0时,它们分别为x,-x,x,x,-x;
当x<0时,它们分别为x,-x,-x,-x,-x.
通过以上分析,它们最多表示两个不同的数,故集合中元素最多含有2个.
6.(一题两空)已知集合A是由偶数组成的,集合B是由奇数组成的,若a∈A,b∈B,则a+b________A,ab________A.(填“∈”或“?”)
解析:因为a是偶数,b是奇数,所以a+b是奇数,ab是偶数,故a+b?A,ab∈A.
答案:? ∈
7.集合A中的元素y满足y∈N且y=-x2+1,若t∈A,则t的值为________.
解析:由y∈N且y=-x2+1≤1,所以y=0或y=1,所以A={0,1}.又因为t∈A,所以t=0或t=1.
答案:0或1
8.已知集合P中的元素x满足:x∈N,且2解析:因为集合P中恰有三个不同元素,且元素x满足x∈N,且2答案:6
9.已知集合A含有两个元素a-3和2a-1,a∈R.
(1)若-3∈A,试求实数a的值;
(2)若a∈A,试求实数a的值.
解:(1)因为-3∈A,所以-3=a-3或-3=2a-1.
若-3=a-3,则a=0.此时集合A含有两个元素-3,-1,符合题意;
若-3=2a-1,则a=-1.此时集合A含有两个元素-4,-3,符合题意.
综上所述,实数a的值为0或-1.
(2)因为a∈A,所以a=a-3或a=2a-1.
当a=a-3时,有0=-3,不成立;
当a=2a-1时,有a=1,此时A中有两个元素-2,1,符合题意.综上知a=1.
10.设集合A中的元素是实数,且满足1?A,且若a∈A,则∈A.若2∈A,写出集合A中的元素.
解:因为2∈A,所以=-1∈A,
所以=∈A,
所以=2,
再求下去仍然只得到2,-1,这三个数,
所以集合A中的元素只有三个:-1,,2.
[B 能力提升]
11.(多选)已知x,y,z为非零实数,代数式+++的值所组成的集合是M,则下列判断正确的是( )
A.0?M
B.2∈M
C.-4∈M
D.4∈M
解析:选CD.x,y,z同为正数时,代数式的值为4,所以4∈M;当x,y,z中只有一个负数或有两个负数时,代数式的值为0;当x,y,z同为负数时,代数式的值为-4.故选CD.
12.若集合A的元素y满足y=x2+1,集合B的元素(x,y)满足y=x2+1(A,B中x∈R,y∈R).则下列选项中元素与集合的关系都正确的是( )
A.2∈A,且2∈B
B.(1,2)∈A,且(1,2)∈B
C.2∈A,且(3,10)∈B
D.(3,10)∈A,且2∈B
解析:选C.集合A中的元素为y,是数集,又y=x2+1≥1,故2∈A,集合B中的元素为点(x,y),且满足y=x2+1,经验证,(3,10)∈B,故选C.
13.(一题两空)已知a∈A且4-a∈A,a∈N且4-a∈N.
(1)若A中只有1个元素,则a=________;
(2)若A中有2个元素,则a=________.
解析:因为a∈A且4-a∈A,
a∈N且4-a∈N,
若a=0,则4-a=4,
此时A含两个元素;
若a=1,则4-a=3,
此时A含两个元素;
若a=2,则4-a=2,
此时A含1个元素.
答案:(1)2 (2)0或1
14.由a,,1组成的集合与由a2,a+b,0组成的集合是同一个集合,求a2
020+b2
020的值.
解:由a,,1组成一个集合,可知a≠0,a≠1,由题意可得=0,即b=0,此时两集合中的元素分别为a,0,1和a2,a,0,因此a2=1,解得a=-1或a=1(不满足集合中元素的互异性,舍去),因此a=-1,且b=0,所以a2
020+b2
020=(-1)2
020+0=1.
[C 拓展探究]
15.定义满足“如果a∈A,b∈A,那么a±b∈A,且ab∈A,且∈A(b≠0)”的集合A为“闭集”.试问数集N,Z,Q,R是否分别为“闭集”?若是,请说明理由;若不是,请举反例说明.
解:①数集N,Z不是“闭集”,例如,3∈N,2∈N,而=1.5?N;3∈Z,-2∈Z,而=-1.5?Z,故N,Z不是闭集.
②数集Q,R是“闭集”.
由于两个有理数a与b的和,差,积,商,
即a±b,ab,(b≠0)仍是有理数,
所以Q是闭集,同理R也是闭集.
HYPERLINK
"http://www.21cnjy.com/"
21世纪教育网(www.21cnjy.com)
教材考点
学习目标
核心素养
集合的概念
了解集合与元素的概念
数学抽象
元素与集合的关系
理解元素与集合的关系,掌握数学中一些常见的数集及其记法
数学抽象、逻辑推理
集合中元素的特性及应用
理解集合中元素的特性,并能利用它们进行解题
数学运算、数学抽象
INCLUDEPICTURE"温馨提示ALLL.TIF"问题导学
预习教材P2-P3,并思考以下问题:
1.集合和元素的概念是什么?
2.如何用字母表示集合和元素?
3.元素和集合之间有哪两种关系?
4.常见的数集有哪些?分别用什么符号表示?
INCLUDEPICTURE"新知初探LLL.TIF"
1.元素与集合的概念
(1)元素:一般地,我们把研究对象统称为元素.元素通常用小写拉丁字母a,b,c,…表示.
(2)集合:把一些元素组成的总体叫做集合(简称为集).集合通常用大写拉丁字母A,B,C,…表示.
(3)集合相等:只要构成两个集合的元素是一样的,我们就称这两个集合是相等的.
(4)元素的特性:确定性、无序性、互异性.
■微思考1
(1)集合中的元素只能是数学中的数、点、代数式吗?
提示:集合中的元素所指的范围非常广泛,可以是数学中的数、点、代数式,也可以是现实生活中的各种各样的事物或人等.
(2)“很瘦的人”能构成集合吗?为什么?
提示:“很瘦的人”不能构成集合.因为它没有确定的标准.如果给定一个集合A,一个研究对象a是不是这个集合中的元素就确定了.
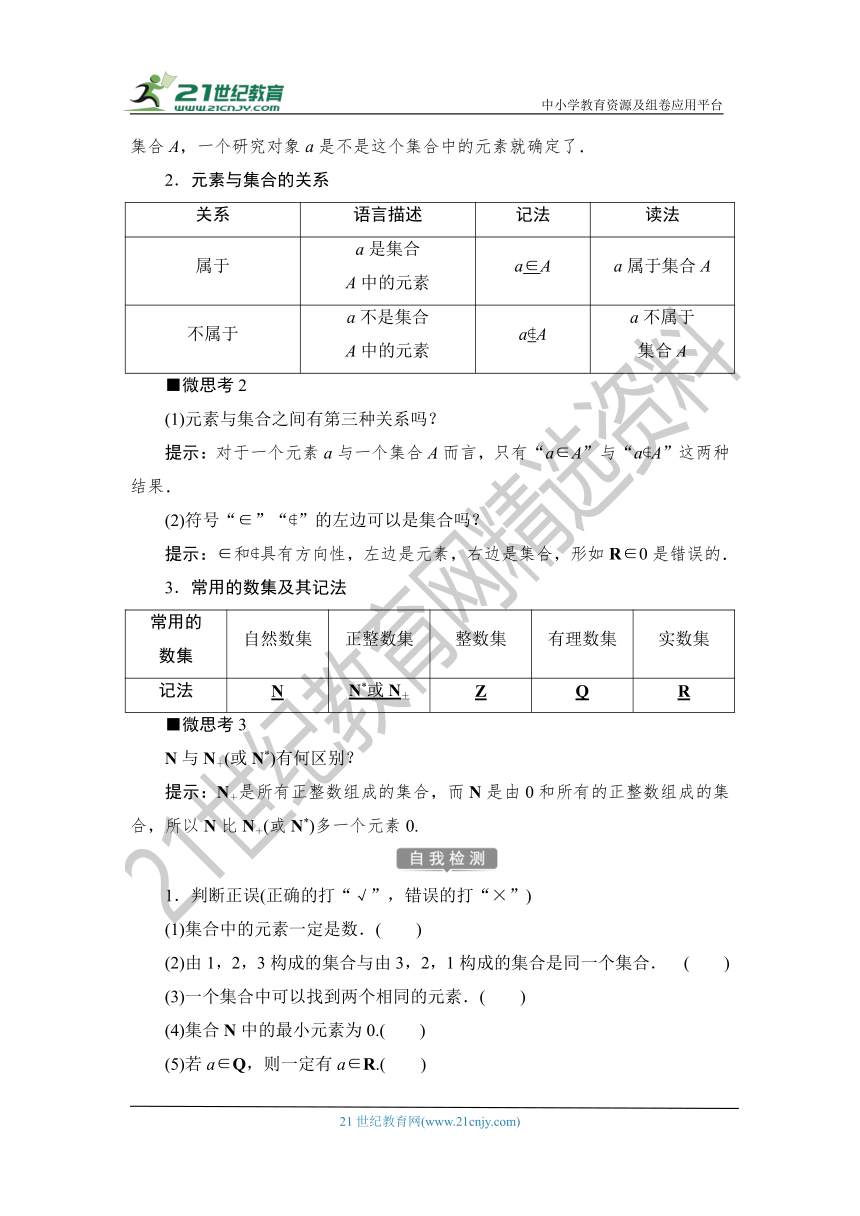
2.元素与集合的关系
关系
语言描述
记法
读法
属于
a是集合A中的元素
a∈A
a属于集合A
不属于
a不是集合A中的元素
a?A
a不属于集合A
■微思考2
(1)元素与集合之间有第三种关系吗?
提示:对于一个元素a与一个集合A而言,只有“a∈A”与“a?A”这两种结果.
(2)符号“∈”“?”的左边可以是集合吗?
提示:∈和?具有方向性,左边是元素,右边是集合,形如R∈0是错误的.
3.常用的数集及其记法
常用的数集
自然数集
正整数集
整数集
有理数集
实数集
记法
N
N
或N+
Z
Q
R
■微思考3
N与N+(或N
)有何区别?
提示:N+是所有正整数组成的集合,而N是由0和所有的正整数组成的集合,所以N比N+(或N
)多一个元素0.
INCLUDEPICTURE"自我检测LLL.TIF"
INCLUDEPICTURE
"../../../../自我检测LLL.TIF"
\
MERGEFORMAT
1.判断正误(正确的打“√”,错误的打“×”)
(1)集合中的元素一定是数.( )
(2)由1,2,3构成的集合与由3,2,1构成的集合是同一个集合. ( )
(3)一个集合中可以找到两个相同的元素.( )
(4)集合N中的最小元素为0.( )
(5)若a∈Q,则一定有a∈R.( )
答案:(1)× (2)√ (3)× (4)√ (5)√
2.由“title”中的字母构成的集合中元素的个数为( )
A.2
B.3
C.4
D.5
解析:选C.由“title”中的字母构成的集合中元素为t,i,l,e,共4个.
3.下列关系①0.21∈Q;②?N
;③-∈N
;④∈N.其中正确的个数是( )
A.0
B.1
C.2
D.3
解析:选C.①是正确的,②中=2∈N
,③中-=-2?N
,④=2∈N是正确的,故①④正确.
4.已知集合M有两个元素3和a+1,且4∈M,则实数a=________.
解析:由题意知a+1=4,即a=3.
答案:3
INCLUDEPICTURE"探究案讲练互动LLL.TIF"
探究点1 集合的概念
INCLUDEPICTURE"例1LLL.TIF"
INCLUDEPICTURE
"../../../../例1LLL.TIF"
\
MERGEFORMAT
2020年9月,我们踏入了心仪的高中校园,找到了自己的班级.则下列对象中能构成一个集合的是哪些?并说明你的理由.
(1)你所在班级中的全体同学;
(2)班级中比较高的同学;
(3)班级中身高超过178
cm的同学;
(4)班级中比较胖的同学;
(5)班级中体重超过75
kg的同学;
(6)学习成绩比较好的同学
【解】 (1)班级中的全体同学是确定的,所以可以构成一个集合.
(2)因为“比较高”无法衡量,所以对象不确定,所以不能构成一个集合.
(3)因为“身高超过178
cm”是确定的,所以可以构成一个集合.
(4)“比较胖”无法衡量,所以对象不确定,所以不能构成一个集合.
(5)“体重超过75
kg”是确定的,所以可以构成一个集合.
(6)“学习成绩比较好”无法衡量,所以对象不确定,所以不能构成一个集合.
判断一组对象能否构成集合的方法
一般地,确认一组对象a1,a2,a3,…,an(a1,a2,…,an均不相同)能否构成集合的过程为:
INCLUDEPICTURE
"../../../../ab4.TIF"
\
MERGEFORMAT
INCLUDEPICTURE"跟踪训练LLL.TIF"
1.(多选)下列各组对象能构成集合的是( )
A.拥有手机的人
B.2020年高考数学难题
C.所有有理数
D.小于π的正整数
解析:选ACD.B选项中“难题”的标准不明确,不符合确定性,显然A,C,D选项中能构成集合,故选ACD.
2.中国男子篮球职业联赛(China
Basketball
Association),简称中职篮(CBA),是由中国篮球协会所主办的跨年度主客场制篮球联赛,是中国最高等级的篮球联赛.下列对象能构成一个集合的是________(填序号).
①2019~2020赛季,CBA的所有队伍;
②CBA中比较著名的队员;
③CBA中得分前五位的球员;
④CBA中比较高的球员.
解析:①CBA的所有队伍是确定的,所以可以构成一个集合.
②“比较著名”没有衡量的标准,对象不确定,所以不能构成一个集合.
③“得分前五位”是确定的,所以可以构成一个集合.
④“比较高”没有衡量的标准,对象不确定,所以不能构成一个集合.
答案:①③
探究点2 元素与集合的关系
(1)集合M是由大于-2且小于1的实数构成的,则下列关系式正确的是( )
A.∈M
B.0?M
C.1∈M
D.-∈M
(2)用符号∈和?填空.
①设集合A是正整数的集合,则0________A,________A,(-1)0________A;
②设集合D是由满足y=x2的有序实数对(x,y)组成的,则-1________D,(-1,1)________D;
③设集合M由可表示为a+b(a∈Z,b∈Z)的实数构成,则0________M,________M,________M.
【解析】 (1)>1,故?M;-2<0<1,故0∈M;1不小于1,故1?M;-2<-<1,故-∈M.故选D.
(2)①0不是正整数,不是正整数,(-1)0=1是正整数;②-1不是有序实数对,所以-1?D,(-1,1)满足y=x2,故(-1,1)∈D;③因为0=0+0×,所以0∈M,因为=1+1×,所以∈M,因为=+1×,?Z,所以?M.
【答案】 (1)D (2)①? ? ∈ ②? ∈ ③∈ ∈ ?
判断元素和集合关系的两种方法
(1)直接法:如果集合中的元素是直接给出的,只要判断该元素在已知集合中是否给出即可.
此时应首先明确集合是由哪些元素构成的.
(2)推理法:对于某些不便直接表示的集合,判断元素与集合的关系时,只要判断该元素是否满足集合中元素所具有的特征即可.此时应首先明确已知集合的元素具有什么属性,即该集合中元素要符合哪种表达式或满足哪些条件.
1.下列关系中,正确的有( )
①∈R;②?Q;③|-3|∈N;④|-|∈Q.
A.1个
B.2个
C.3个
D.4个
解析:选C.是实数,是无理数,|-3|=3是非负整数,|-|=是无理数.
因此①②③正确,④错误.
2.已知集合A中元素满足2x+a>0,a∈R.若1?A,2∈A,则实数a的取值范围为________.
解析:因为1?A,2∈A,
所以
即-4
INCLUDEPICTURE"例3LLL.TIF"
已知集合A中含有两个元素a和a2,若1∈A,则实数a的值为________.
【解析】 若1∈A,则a=1或a2=1,
即a=±1.
当a=1时,集合A中有重复元素,
所以a≠1;
当a=-1时,集合A含有两个元素1,-1,符合元素的互异性,所以a=-1.
【答案】 -1
1.(变条件)若去掉本例中的条件“1∈A”,则实数a的取值范围是什么?
解:因为集合A中含有两个元素a和a2,
所以a≠a2,
即a≠0且a≠1.
2.(变条件)若将本例中的“1∈A”改为“2∈A”,则a为何值?
解:因为2∈A,
所以a=2或a2=2,
即a=2或a=±.
3.(变条件)若由a和a2构成的集合只有一个元素,则a为何值?
解:因为由a和a2构成的集合只有一个元素,所以a=a2,即a=0或a=1.
由集合中元素的特征求解字母取值(范围)的步骤
INCLUDEPICTURE
"../../../../MF1.TIF"
\
MERGEFORMAT
INCLUDEPICTURE"跟踪训练LLL.TIF"
1.若集合M中的三个元素是△ABC的三边长,则△ABC一定不是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形
解析:选D.由集合中元素的互异性可知,集合中的任何两个元素都不相同,故选D.
2.若集合A中有三个元素x,x+1,1,集合B中也有三个元素x,x+x2,x2,且A=B,求实数x的值.
解:因为A=B,
所以或
解得x=±1.经检验,x=1不适合集合元素的互异性,而x=-1适合,
所以x=-1.
INCLUDEPICTURE"自测案当堂达标LLL.TIF"
1.考察下列每组对象,能组成一个集合的是( )
①一中高一年级聪明的学生;②直角坐标系中横、纵坐标相等的点;③不小于3的正整数;④的近似值.
A.①②
B.③④
C.②③
D.①③
解析:选C.①“一中高一年级聪明的学生”的标准不确定,因而不能构成集合;②“直角坐标系中横、纵坐标相等的点”的标准确定,能构成集合;③“不小于3的正整数”的标准确定,能构成集合;④“的近似值”的标准不确定,不能构成集合.
2.下列结论中,不正确的是( )
A.若a∈N,则?N
B.若a∈Z,则a2∈Z
C.若a∈Q,则|a|∈Q
D.若a∈R,则∈R
解析:选A.A不正确.反例a=1∈N,=1∈N.
3.若以方程x2-5x+6=0和x2-x-2=0的解为元素组成集合M,则M中元素的个数为( )
A.1
B.2
C.3
D.4
解析:选C.方程x2-5x+6=0的解为x=2或x=3,x2-x-2=0的解为x=2或x=-1,所以集合M中含有3个元素.
4.用适当的符号填空:
已知集合A中的元素x是被3除余2的整数,则有:
17________A;-5________A.
解析:由题意可设x=3k+2,k∈Z,
令3k+2=17得,k=5∈Z
.
所以17∈A.令3k+2=-5得,
k=-?Z.所以-5?A.
答案:∈ ?
5.已知集合A是由0,m,m2-3m+2三个元素构成的集合,且2∈A,则实数m=________.
解析:由题意知,m=2或m2-3m+2=2,
解得m=2或m=0或m=3,经验证,
当m=0或m=2时,
不满足集合中元素的互异性,
当m=3时,满足题意,
故m=3.
答案:3INCLUDEPICTURE"应用案巩固提升LLL.TIF"
[A 基础达标]
1.有以下说法,其中正确的是( )
①接近于0的数的全体构成一个集合;
②正方体的全体构成一个集合;
③未来世界的高科技产品构成一个集合;
④不大于3的所有自然数构成一个集合.
A.①②
B.②③
C.③④
D.②④
解析:选D.在①中,接近于0的数的全体不能构成一个集合,故①错误;在②中,正方体的全体能构成一个集合,故②正确;在③中,未来世界的高科技产品不能构成一个集合,故③错误;在④中,不大于3的所有自然数能构成一个集合,故④正确.
2.给出下列关系:①∈R;②∈Q;③-3?Z;④-?N,其中正确的个数为( )
A.1
B.2
C.3
D.4
解析:选B.是实数,①正确;是无理数,②错误;-3是整数,③错误;-是无理数,④正确.故选B.
3.设A是方程2x2+ax+2=0的解集,且2∈A,则实数a的值为( )
A.-5
B.-4
C.4
D.5
解析:选A.因为2∈A,
所以2×22+2a+2=0,
解得a=-5.
4.设集合M是由不小于2的数组成的集合,a=,则下列关系中正确的是( )
A.a∈M
B.a?M
C.a=M
D.a≠M
解析:选B.因为集合M是由不小于2的数组成的集合,a=,所以a不是集合M中的元素,故a?M.
5.由实数x,-x,|x|,,-所组成的集合,最多含有( )
A.2个元素
B.3个元素
C.4个元素
D.5个元素
解析:选A.=|x|,-=-x.
当x=0时,它们均为0;
当x>0时,它们分别为x,-x,x,x,-x;
当x<0时,它们分别为x,-x,-x,-x,-x.
通过以上分析,它们最多表示两个不同的数,故集合中元素最多含有2个.
6.(一题两空)已知集合A是由偶数组成的,集合B是由奇数组成的,若a∈A,b∈B,则a+b________A,ab________A.(填“∈”或“?”)
解析:因为a是偶数,b是奇数,所以a+b是奇数,ab是偶数,故a+b?A,ab∈A.
答案:? ∈
7.集合A中的元素y满足y∈N且y=-x2+1,若t∈A,则t的值为________.
解析:由y∈N且y=-x2+1≤1,所以y=0或y=1,所以A={0,1}.又因为t∈A,所以t=0或t=1.
答案:0或1
8.已知集合P中的元素x满足:x∈N,且2
9.已知集合A含有两个元素a-3和2a-1,a∈R.
(1)若-3∈A,试求实数a的值;
(2)若a∈A,试求实数a的值.
解:(1)因为-3∈A,所以-3=a-3或-3=2a-1.
若-3=a-3,则a=0.此时集合A含有两个元素-3,-1,符合题意;
若-3=2a-1,则a=-1.此时集合A含有两个元素-4,-3,符合题意.
综上所述,实数a的值为0或-1.
(2)因为a∈A,所以a=a-3或a=2a-1.
当a=a-3时,有0=-3,不成立;
当a=2a-1时,有a=1,此时A中有两个元素-2,1,符合题意.综上知a=1.
10.设集合A中的元素是实数,且满足1?A,且若a∈A,则∈A.若2∈A,写出集合A中的元素.
解:因为2∈A,所以=-1∈A,
所以=∈A,
所以=2,
再求下去仍然只得到2,-1,这三个数,
所以集合A中的元素只有三个:-1,,2.
[B 能力提升]
11.(多选)已知x,y,z为非零实数,代数式+++的值所组成的集合是M,则下列判断正确的是( )
A.0?M
B.2∈M
C.-4∈M
D.4∈M
解析:选CD.x,y,z同为正数时,代数式的值为4,所以4∈M;当x,y,z中只有一个负数或有两个负数时,代数式的值为0;当x,y,z同为负数时,代数式的值为-4.故选CD.
12.若集合A的元素y满足y=x2+1,集合B的元素(x,y)满足y=x2+1(A,B中x∈R,y∈R).则下列选项中元素与集合的关系都正确的是( )
A.2∈A,且2∈B
B.(1,2)∈A,且(1,2)∈B
C.2∈A,且(3,10)∈B
D.(3,10)∈A,且2∈B
解析:选C.集合A中的元素为y,是数集,又y=x2+1≥1,故2∈A,集合B中的元素为点(x,y),且满足y=x2+1,经验证,(3,10)∈B,故选C.
13.(一题两空)已知a∈A且4-a∈A,a∈N且4-a∈N.
(1)若A中只有1个元素,则a=________;
(2)若A中有2个元素,则a=________.
解析:因为a∈A且4-a∈A,
a∈N且4-a∈N,
若a=0,则4-a=4,
此时A含两个元素;
若a=1,则4-a=3,
此时A含两个元素;
若a=2,则4-a=2,
此时A含1个元素.
答案:(1)2 (2)0或1
14.由a,,1组成的集合与由a2,a+b,0组成的集合是同一个集合,求a2
020+b2
020的值.
解:由a,,1组成一个集合,可知a≠0,a≠1,由题意可得=0,即b=0,此时两集合中的元素分别为a,0,1和a2,a,0,因此a2=1,解得a=-1或a=1(不满足集合中元素的互异性,舍去),因此a=-1,且b=0,所以a2
020+b2
020=(-1)2
020+0=1.
[C 拓展探究]
15.定义满足“如果a∈A,b∈A,那么a±b∈A,且ab∈A,且∈A(b≠0)”的集合A为“闭集”.试问数集N,Z,Q,R是否分别为“闭集”?若是,请说明理由;若不是,请举反例说明.
解:①数集N,Z不是“闭集”,例如,3∈N,2∈N,而=1.5?N;3∈Z,-2∈Z,而=-1.5?Z,故N,Z不是闭集.
②数集Q,R是“闭集”.
由于两个有理数a与b的和,差,积,商,
即a±b,ab,(b≠0)仍是有理数,
所以Q是闭集,同理R也是闭集.
HYPERLINK
"http://www.21cnjy.com/"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
