1.1.3.1 【教案+测评】2019人教A版 必修 第一册 第一章 集合与常用逻辑用语 第三节 集合的基本运算 第一课时 并集与交集
文档属性
| 名称 | 1.1.3.1 【教案+测评】2019人教A版 必修 第一册 第一章 集合与常用逻辑用语 第三节 集合的基本运算 第一课时 并集与交集 |
|
|
| 格式 | doc | ||
| 文件大小 | 670.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 21:05:48 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
INCLUDEPICTURE"导学聚焦LLL.TIF"
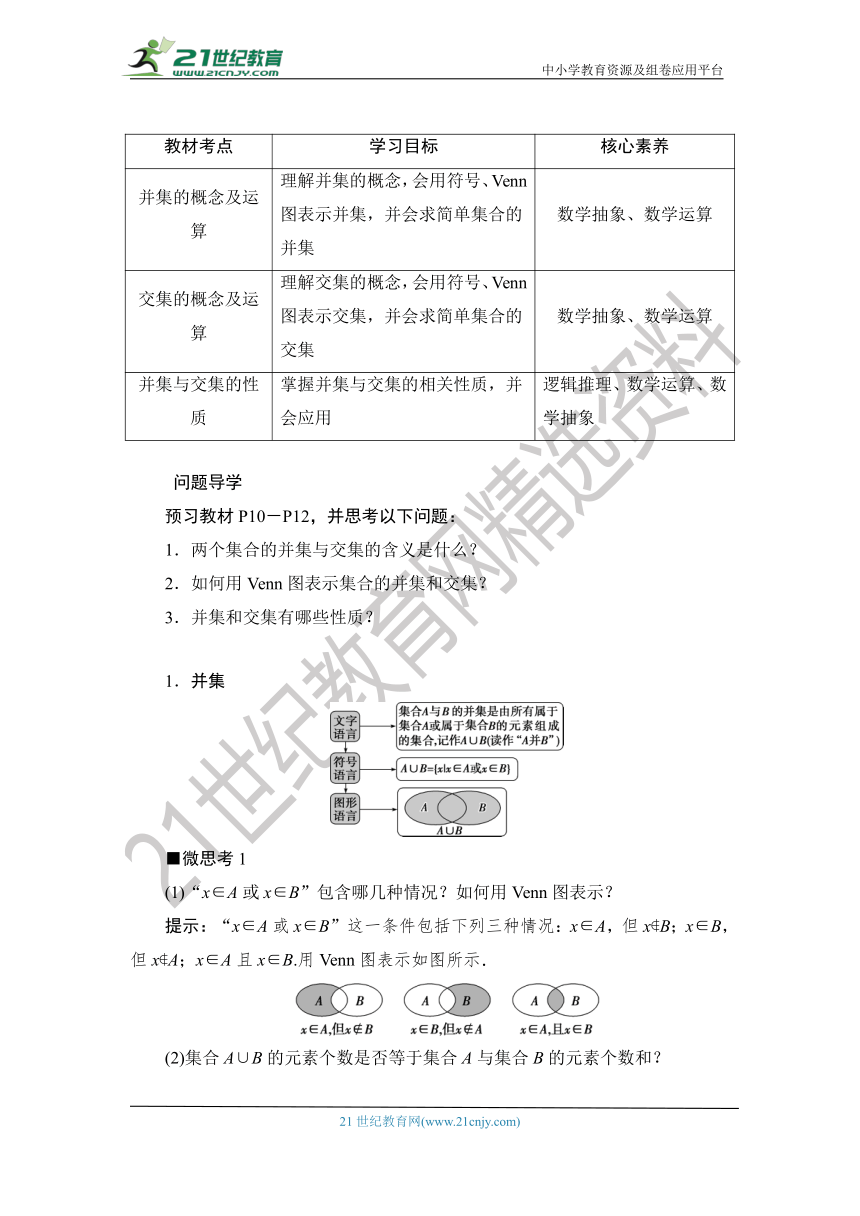
教材考点
学习目标
核心素养
并集的概念及运算
理解并集的概念,会用符号、Venn图表示并集,并会求简单集合的并集
数学抽象、数学运算
交集的概念及运算
理解交集的概念,会用符号、Venn图表示交集,并会求简单集合的交集
数学抽象、数学运算
并集与交集的性质
掌握并集与交集的相关性质,并会应用
逻辑推理、数学运算、数学抽象
INCLUDEPICTURE"预习案自主学习LLL.TIF"
INCLUDEPICTURE"温馨提示ALLL.TIF"
问题导学
预习教材P10-P12,并思考以下问题:
1.两个集合的并集与交集的含义是什么?
2.如何用Venn图表示集合的并集和交集?
3.并集和交集有哪些性质?
INCLUDEPICTURE"新知初探LLL.TIF"
1.并集
INCLUDEPICTURE
"../../../../C1-7.TIF"
\
MERGEFORMAT
■微思考1
(1)“x∈A或x∈B”包含哪几种情况?如何用Venn图表示?
提示:“x∈A或x∈B”这一条件包括下列三种情况:x∈A,但x?B;x∈B,但x?A;x∈A且x∈B.用Venn图表示如图所示.
INCLUDEPICTURE
"../../../../JN4.tif"
\
MERGEFORMAT
(2)集合A∪B的元素个数是否等于集合A与集合B的元素个数和?
提示:不一定等于.A∪B的元素个数小于或等于集合A与集合B的元素个数和.
2.交集
INCLUDEPICTURE
"../../../../C1-8.TIF"
\
MERGEFORMAT
■微思考2
当集合A,B无公共元素时,A与B有交集吗?
提示:当集合A,B无公共元素时,A与B有交集,它们的交集是空集.
3.并集与交集的运算性质
并集的运算性质
交集的运算性质
A∪B=B∪A
A∩B=B∩A
A∪A=A
A∩A=A
A∪?=A
A∩?=?
■微思考3
对于任意两个集合A,B.
(1)A∩B与A有什么关系?A∪B与A有什么关系?
提示:(A∩B)?A;A?(A∪B).
(2)若A∩B=A,则A与B有什么关系?
若A∪B=A,则A与B有什么关系?
提示:若A∩B=A,则A?B;若A∪B=A,则B?A.
INCLUDEPICTURE"自我检测LLL.TIF"
INCLUDEPICTURE
"../../../../自我检测LLL.TIF"
\
MERGEFORMAT
1.判断正误(正确的打“√”,错误的打“×”)
(1)A∪B的元素个数等于集合A中元素的个数与集合B中元素个数的和.( )
(2)并集定义中的“或”能改为“和”.( )
(3)A∩B是由属于A且属于B的所有元素组成的集合.( )
(4)交集的元素个数一定比任何一个集合的元素个数都少.( )
(5)若A∩B=A∩C,则必有B=C.( )
答案:(1)× (2)× (3)√ (4)× (5)×
2.已知集合M={-1,0,1},N={0,1,2},则M∪N=( )
A.{-1,0,1}
B.{-1,0,1,2}
C.{-1,0,2}
D.{0,1}
解析:选B.M∪N表示属于M或属于N的元素组成的集合,故M∪N={-1,0,1,2}.
3.设集合A={1,3,5,7},B={x|2≤x≤5},则A∩B=( )
A.{1,3}
B.{3,5}
C.{5,7}
D.{1,7}
解析:选B.因为A={1,3,5,7},B={x|2≤x≤5},所以A∩B={3,5}.
4.已知集合M={x|-1解析:在数轴上表示出集合,如图所示,
INCLUDEPICTURE
"../../../../C1-9.TIF"
\
MERGEFORMAT
由图知M∩N={x|-1答案:{x|-1INCLUDEPICTURE"探究案讲练互动LLL.TIF"
INCLUDEPICTURE
"../../../../探究案讲练互动LLL.TIF"
\
MERGEFORMAT
探究点1 集合并集的运算
INCLUDEPICTURE"例1LLL.TIF"
INCLUDEPICTURE
"../../../../例1LLL.TIF"
\
MERGEFORMAT
(1)设集合A={1,2,3},B={2,3,4},则A∪B=( )
A.{1,2,3,4}
B.{1,2,3}
C.{2,3,4}
D.{1,3,4}
(2)已知集合P={x|-1A.{x|-1B.{x|0C.{x|-1D.{x|1【解析】 (1)由题意A∪B={1,2,3,4}.
(2)因为P={x|-1Q={x|0INCLUDEPICTURE
"../../../../ab21.TIF"
\
MERGEFORMAT
所以P∪Q={x|-1【答案】 (1)A (2)A
INCLUDEPICTURE
"../../../../CK2.TIF"
\
MERGEFORMAT
INCLUDEPICTURE"跟踪训练LLL.TIF"
INCLUDEPICTURE
"../../../../跟踪训练LLL.TIF"
\
MERGEFORMAT
1.(多选)满足{1,3}∪A={1,3,5}的集合A可能是( )
A.{5}
B.{1,5}
C.{3}
D.{1,3}
解析:选AB.由{1,3}∪A={1,3,5}知,A?{1,3,5},且A中至少有1个元素5,故选AB.
2.若集合M={x|-3<x≤5},N={x|x<-5或x>5},则M∪N=________.
解析:将-3<x≤5,x<-5或x>5在数轴上表示出来.
INCLUDEPICTURE
"../../../../MF15.TIF"
\
MERGEFORMAT
所以M∪N={x|x<-5或x>-3}.
答案:{x|x<-5或x>-3}
探究点2 集合交集的运算
INCLUDEPICTURE"例2LLL.TIF"
INCLUDEPICTURE
"../../../../例2LLL.TIF"
\
MERGEFORMAT
(1)设集合M={m∈Z|-3<m<2},N={n∈Z|-1≤n≤3},则M∩N=( )
A.{0,1}
B.{-1,0,1}
C.{0,1,2}
D.{-1,0,1,2}
(2)已知集合A={x|2<x<4},B={x|x<3或x>5},则A∩B=( )
A.{x|2<x<5}
B.{x|x<4或x>5}
C.{x|2<x<3}
D.{x|x<2或x>5}
【解析】 (1)易知M={-2,-1,0,1},N={-1,0,1,2,3},据交集定义可知M∩N={-1,0,1},故选B.
(2)将集合A、B画在数轴上,如图.
INCLUDEPICTURE
"../../../../C1-10.TIF"
\
MERGEFORMAT
由图可知A∩B={x|2【答案】 (1)B (2)C
求两个集合的交集的方法
(1)对于元素个数有限的集合,逐个挑出两个集合的公共元素即可.
(2)对于元素个数无限的集合,一般借助数轴求交集,两个集合的交集等于两个集合在数轴上的相应图形所覆盖的公共范围,要注意端点值的取舍.
INCLUDEPICTURE"跟踪训练LLL.TIF"
INCLUDEPICTURE
"../../../../跟踪训练LLL.TIF"
\
MERGEFORMAT
1.若集合A={x|-2A.{x|-1B.{x|-2C.{x|-2D.{x|0解析:选D.如图,
INCLUDEPICTURE
"../../../../S1-16.TIF"
\
MERGEFORMAT
因为A={x|-2B={x|0所以A∩B={x|02.(多选)已知全集U=R,集合M={x|-2≤x-1≤2}和N={x|x=2k-1,k∈N
}关系的Venn图如图所示,则阴影部分表示的集合中的元素有( )
INCLUDEPICTURE
"../../../../JN5.tif"
\
MERGEFORMAT
A.-1
B.0
C.1
D.3
解析:选CD.因为M={x|-1≤x≤3},N={x|x=2k-1,k∈N
},所以M∩N={1,3},故选CD.
探究点3 交集、并集性质的应用
INCLUDEPICTURE"例3LLL.TIF"
INCLUDEPICTURE
"../../../../例3LLL.TIF"
\
MERGEFORMAT
已知集合A={x|20)}.
(1)若A∪B=B,求a的取值范围;
(2)若A∩B=?,求a的取值范围.
【解】 (1)因为A∪B=B,所以A?B,
INCLUDEPICTURE
"../../../../ab25.TIF"
\
MERGEFORMAT
观察数轴可知,所以≤a≤2.
(2)A∩B=?有两类情况:B在A的左边和B在A的右边,如图.
INCLUDEPICTURE
"../../../../ab26.TIF"
\
MERGEFORMAT
观察数轴可知,a≥4或3a≤2,又a>0,
所以0INCLUDEPICTURE"互动探究LLL.TIF"
INCLUDEPICTURE
"../../../../互动探究LLL.TIF"
\
MERGEFORMAT
(变条件)本例条件下,若A∩B={x|3解:画出数轴如图,
INCLUDEPICTURE
"../../../../ab27.TIF"
\
MERGEFORMAT
观察图形可知即a=3.
利用集合交集、并集的性质解题的方法
(1)在利用集合的交集、并集性质解题时,常常会遇到A∩B=A,A∪B=B等这类问题,解答时常借助于交、并集的定义及上节学习的集合间的关系去分析,如A∩B=A?A?B,A∪B=B?A?B等,解答时应灵活处理.
(2)当集合B?A时,如果集合A是一个确定的集合,而集合B不确定,运算时要考虑B=?的情况,切不可漏掉.
INCLUDEPICTURE"跟踪训练LLL.TIF"
INCLUDEPICTURE
"../../../../跟踪训练LLL.TIF"
\
MERGEFORMAT
1.已知M={1,2,a2-3a-1},N={-1,a,3},M∩N={3},则实数a的值为________.
解析:因为M∩N={3},
所以a2-3a-1=3,
解得a=-1或a=4.
又N={-1,a,3},所以a≠-1,
所以a=4.
答案:4
2.(一题两空)已知A={x|a5}.
(1)若A∩B=A,则a的取值范围为________;
(2)若A∪B=R,则a的取值范围为________.
解析:(1)因为A∩B=A,所以A?B,
所以a≥5或a+8<-1,
即a≥5或a<-9.
(2)在数轴上标出集合A,B,如图.
INCLUDEPICTURE
"../../../../ab28.TIF"
\
MERGEFORMAT
要使A∪B=R,则
解得-3≤a<-1.
综上,可知a的取值范围为{a|-3≤a<-1}.
答案:(1)a≥5或a<-9 (2)-3≤a<-1
INCLUDEPICTURE"自测案当堂达标LLL.TIF"
INCLUDEPICTURE
"../../../../自测案当堂达标LLL.TIF"
\
MERGEFORMAT
1.设集合A={1,2},B={1,2,3},C={2,3,4},则(A∩B)∪C等于( )
A.{1,2,3}
B.{1,2,4}
C.{2,3,4}
D.{1,2,3,4}
解析:选D.因为A={1,2},B={1,2,3},
所以A∩B={1,2}.
又C={2,3,4},
所以(A∩B)∪C={1,2}∪{2,3,4}={1,2,3,4}.
2.(2020·平顶山高一检测)已知集合M={0,1,3},N={x|x=3a,a∈M},则M∪N=( )
A.{0}
B.{0,3}
C.{1,3,9}
D.{0,1,3,9}
解析:选D.因为M={0,1,3},
N={x|x=3a,a∈M}={0,3,9},
所以M∪N={0,1,3,9}.
3.已知A={(x,y)|x+y=3},B={(x,y)|x-y=1},则A∩B=( )
A.{2,1}
B.{x=2,y=1}
C.{(2,1)}
D.(2,1)
解析:选C.A∩B=
={(2,1)}.
4.已知集合A={x|3≤x≤9},B={x|2a}.
(1)求A∪B;
(2)若B∩C=?,求实数a的取值范围.
解:(1)由A={x|3≤x≤9},B={x|2(2)由B∩C=?,B={x|2C={x|x>a},得a≥5,
故实数a的取值范围是{a|a≥5}.
INCLUDEPICTURE"应用案巩固提升LLL.TIF"
INCLUDEPICTURE
"../../../../应用案巩固提升LLL.TIF"
\
MERGEFORMAT
[A 基础达标]
1.设集合M={x|x2+2x=0,x∈R},N={x|x2-2x=0,x∈R},则M∪N等于( )
A.{0}
B.{0,2}
C.{-2,0}
D.{-2,0,2}
解析:选D.集合M={0,-2},N={0,2},故M∪N={-2,0,2},选D.
2.(2020·烟台高一检测)已知集合M={0,1,2},N={x|x=2a-1,a∈N
},则M∩N=( )
A.{0}
B.{1,2}
C.{1}
D.{2}
解析:选C.因为N={1,3,5,…},M={0,1,2},所以M∩N={1}.
3.已知集合P={x|x<3},Q={x|-1≤x≤4},则P∪Q=( )
A.{x|-1≤x<3}
B.{x|-1≤x≤4}
C.{x|x≤4}
D.{x|x≥-1}
解析:选C.在数轴上表示两个集合,如图.
INCLUDEPICTURE
"../../../../MF20.TIF"
\
MERGEFORMAT
易知P∪Q={x|x≤4}.
4.已知集合M={-1,1},则满足M∪N={-1,1,2}的集合N的个数是( )
A.1
B.2
C.3
D.4
解析:选D.依题意,得满足M∪N={-1,1,2}的集合N有{2},{-1,2},{1,2},{-1,1,2},共4个.
5.设集合A={x|-1≤x<2},B={x|xA.a<2
B.a>-2
C.a>-1
D.-1解析:选C.在数轴上表示出集合A、B即可知选C.
INCLUDEPICTURE
"../../../../S1-20.TIF"
\
MERGEFORMAT
6.(一题两空)若集合A={x|-1<x<5},B={x|x≤-1或x≥4},则A∪B=________;A∩B=________.
解析:如图所示,借助数轴可知:
INCLUDEPICTURE
"../../../../MF25.TIF"
\
MERGEFORMAT
A∪B=R,A∩B={x|4≤x<5}.
答案:R {x|4≤x<5}
7.若集合A={x|x≤2},B={x|x≥a},且满足A∩B={2},则实数a=________.
解析:当a>2时,A∩B=?;
当a<2时,A∩B={x|a≤x≤2};
当a=2时,A∩B={2}.
综上,a=2.
答案:2
8.已知集合A={3,2a},B={a,b}.若A∩B={2},则A∪B=________.
解析:因为A∩B={2},所以2a=2,即a=1.所以b=2,所以A={3,2},B={1,2},所以A∪B={1,2,3}.
答案:{1,2,3}
9.设A={x|x2+ax+12=0},B={x|x2+3x+2b=0},A∩B={2},C={2,-3}.
(1)求a,b的值及A,B;
(2)求(A∪B)∩C.
解:(1)因为A∩B={2},
所以4+2a+12=0,4+6+2b=0,
即a=-8,b=-5,
所以A={x|x2-8x+12=0}={2,6},
B={x|x2+3x-10=0}={2,-5}.
(2)因为A∪B={-5,2,6},C={2,-3},
所以(A∪B)∩C={2}.
10.已知集合A={x|x≥3},B={x|1≤x≤7},C={x|x≥a-1}.
(1)求A∩B,A∪B;
(2)若C∪A=A,求实数a的取值范围.
解:(1)因为A={x|x≥3},B={x|1≤x≤7},所以A∩B={x|3≤x≤7},A∪B={x|x≥1}.
(2)因为C∪A=A,A={x|x≥3},C={x|x≥a-1},
所以C?A,所以a-1≥3,即a≥4.
[B 能力提升]
11.(多选)已知集合A={x|x2-3x+2=0},B={x|ax-2=0},若A∩B=B,则实数a的值为( )
A.0
B.1
C.2
D.3
解析:选ABC.A={x|x2-3x+2=0}={1,2},
因为A∩B=B,所以B?A.
当B=?时,ax-2=0无解,所以a=0.
当B≠?时,x=,所以=1或=2,解得a=2或a=1.
所以实数a的值为0或1或2.故选ABC.
12.已知集合A={x|x2-px-2=0},B={x|x2+qx+r=0},且A∪B={-2,1,5},A∩B={-2},则p+q+r=________.
解析:因为A∩B={-2},
所以-2∈A且-2∈B,将x=-2代入x2-px-2=0,得p=-1,
所以A={1,-2},
因为A∪B={-2,1,5},A∩B={-2},
所以B={-2,5},
所以q=-[(-2)+5]=-3,r=(-2)×5=-10,
所以p+q+r=-14.
答案:-14
13.(一题两空)设集合A={2,-1,x2-x+1},B={2y,-4,x+4},C={-1,7},且A∩B=C,则x+y=________,A∪B=________.
解析:由A={2,-1,x2-x+1},B={2y,-4,x+4},C={-1,7}且A∩B=C,得
7∈A,7∈B且-1∈B,
所以在集合A中x2-x+1=7,
解得x=-2或3.
当x=-2时,在集合B中,x+4=2,
又2∈A,故2∈A∩B=C,
但2?C,故x=-2不合题意,舍去;
当x=3时,在集合B中,x+4=7,
故有2y=-1,解得y=-,
经检验满足A∩B=C.
综上知,所求x=3,y=-.所以x+y=.
此时A={2,-1,7},B={-1,-4,7},
故A∪B={-1,2,-4,7}.
答案: {-1,-4,2,7}
14.已知集合A={x|2a+1≤x≤3a-5},B={x|x<-1或x>16},分别根据下列条件求实数a的取值范围.
(1)A∩B=?;
(2)A?(A∩B).
解:(1)若A=?,则A∩B=?成立.此时2a+1>3a-5,
即a<6.
若A≠?,如图所示,
INCLUDEPICTURE
"../../../../S1-23.TIF"
\
MERGEFORMAT
则
解得6≤a≤7.综上,满足条件A∩B=?的实数a的取值范围是{a|a≤7}.
(2)因为A?(A∩B),所以A∩B=A,
即A?B.
显然A=?满足条件,此时a<6.
若A≠?,如图所示,
INCLUDEPICTURE
"../../../../S1-22.TIF"
\
MERGEFORMAT
则或
由解得a∈?;
由解得a>.
综上,满足条件A?(A∩B)的实数a的取值范围是{a|a<6或a>}.
[C 拓展探究]
15.某网店统计了连续三天售出商品的种类情况:第一天售出19种商品,第二天售出13种商品,第三天售出18种商品;前两天都售出的商品有3种,后两天都售出的商品有4种.则该网店
(1)第一天售出但第二天未售出的商品有多少种?
(2)这三天售出的商品最少有多少种?
解:设三天都售出的商品有x种,第一天售出,第二天未售出,且第三天售出的商品有y种,则三天售出商品的种类关系如图所示.
INCLUDEPICTURE
"../../../../HY1-1.TIF"
\
MERGEFORMAT
由图可知:(1)第一天售出但第二天未售出的商品有19-(3-x)-x=16(种).
(2)这三天售出的商品有(16-y)+y+x+(3-x)+(6+x)+(4-x)+(14-y)=43-y(种).
由于所以0≤y≤14.
所以(43-y)min=43-14=29.
HYPERLINK
"http://www.21cnjy.com/"
21世纪教育网(www.21cnjy.com)
INCLUDEPICTURE"导学聚焦LLL.TIF"
教材考点
学习目标
核心素养
并集的概念及运算
理解并集的概念,会用符号、Venn图表示并集,并会求简单集合的并集
数学抽象、数学运算
交集的概念及运算
理解交集的概念,会用符号、Venn图表示交集,并会求简单集合的交集
数学抽象、数学运算
并集与交集的性质
掌握并集与交集的相关性质,并会应用
逻辑推理、数学运算、数学抽象
INCLUDEPICTURE"预习案自主学习LLL.TIF"
INCLUDEPICTURE"温馨提示ALLL.TIF"
问题导学
预习教材P10-P12,并思考以下问题:
1.两个集合的并集与交集的含义是什么?
2.如何用Venn图表示集合的并集和交集?
3.并集和交集有哪些性质?
INCLUDEPICTURE"新知初探LLL.TIF"
1.并集
INCLUDEPICTURE
"../../../../C1-7.TIF"
\
MERGEFORMAT
■微思考1
(1)“x∈A或x∈B”包含哪几种情况?如何用Venn图表示?
提示:“x∈A或x∈B”这一条件包括下列三种情况:x∈A,但x?B;x∈B,但x?A;x∈A且x∈B.用Venn图表示如图所示.
INCLUDEPICTURE
"../../../../JN4.tif"
\
MERGEFORMAT
(2)集合A∪B的元素个数是否等于集合A与集合B的元素个数和?
提示:不一定等于.A∪B的元素个数小于或等于集合A与集合B的元素个数和.
2.交集
INCLUDEPICTURE
"../../../../C1-8.TIF"
\
MERGEFORMAT
■微思考2
当集合A,B无公共元素时,A与B有交集吗?
提示:当集合A,B无公共元素时,A与B有交集,它们的交集是空集.
3.并集与交集的运算性质
并集的运算性质
交集的运算性质
A∪B=B∪A
A∩B=B∩A
A∪A=A
A∩A=A
A∪?=A
A∩?=?
■微思考3
对于任意两个集合A,B.
(1)A∩B与A有什么关系?A∪B与A有什么关系?
提示:(A∩B)?A;A?(A∪B).
(2)若A∩B=A,则A与B有什么关系?
若A∪B=A,则A与B有什么关系?
提示:若A∩B=A,则A?B;若A∪B=A,则B?A.
INCLUDEPICTURE"自我检测LLL.TIF"
INCLUDEPICTURE
"../../../../自我检测LLL.TIF"
\
MERGEFORMAT
1.判断正误(正确的打“√”,错误的打“×”)
(1)A∪B的元素个数等于集合A中元素的个数与集合B中元素个数的和.( )
(2)并集定义中的“或”能改为“和”.( )
(3)A∩B是由属于A且属于B的所有元素组成的集合.( )
(4)交集的元素个数一定比任何一个集合的元素个数都少.( )
(5)若A∩B=A∩C,则必有B=C.( )
答案:(1)× (2)× (3)√ (4)× (5)×
2.已知集合M={-1,0,1},N={0,1,2},则M∪N=( )
A.{-1,0,1}
B.{-1,0,1,2}
C.{-1,0,2}
D.{0,1}
解析:选B.M∪N表示属于M或属于N的元素组成的集合,故M∪N={-1,0,1,2}.
3.设集合A={1,3,5,7},B={x|2≤x≤5},则A∩B=( )
A.{1,3}
B.{3,5}
C.{5,7}
D.{1,7}
解析:选B.因为A={1,3,5,7},B={x|2≤x≤5},所以A∩B={3,5}.
4.已知集合M={x|-1
INCLUDEPICTURE
"../../../../C1-9.TIF"
\
MERGEFORMAT
由图知M∩N={x|-1
INCLUDEPICTURE
"../../../../探究案讲练互动LLL.TIF"
\
MERGEFORMAT
探究点1 集合并集的运算
INCLUDEPICTURE"例1LLL.TIF"
INCLUDEPICTURE
"../../../../例1LLL.TIF"
\
MERGEFORMAT
(1)设集合A={1,2,3},B={2,3,4},则A∪B=( )
A.{1,2,3,4}
B.{1,2,3}
C.{2,3,4}
D.{1,3,4}
(2)已知集合P={x|-1
(2)因为P={x|-1
"../../../../ab21.TIF"
\
MERGEFORMAT
所以P∪Q={x|-1
INCLUDEPICTURE
"../../../../CK2.TIF"
\
MERGEFORMAT
INCLUDEPICTURE"跟踪训练LLL.TIF"
INCLUDEPICTURE
"../../../../跟踪训练LLL.TIF"
\
MERGEFORMAT
1.(多选)满足{1,3}∪A={1,3,5}的集合A可能是( )
A.{5}
B.{1,5}
C.{3}
D.{1,3}
解析:选AB.由{1,3}∪A={1,3,5}知,A?{1,3,5},且A中至少有1个元素5,故选AB.
2.若集合M={x|-3<x≤5},N={x|x<-5或x>5},则M∪N=________.
解析:将-3<x≤5,x<-5或x>5在数轴上表示出来.
INCLUDEPICTURE
"../../../../MF15.TIF"
\
MERGEFORMAT
所以M∪N={x|x<-5或x>-3}.
答案:{x|x<-5或x>-3}
探究点2 集合交集的运算
INCLUDEPICTURE"例2LLL.TIF"
INCLUDEPICTURE
"../../../../例2LLL.TIF"
\
MERGEFORMAT
(1)设集合M={m∈Z|-3<m<2},N={n∈Z|-1≤n≤3},则M∩N=( )
A.{0,1}
B.{-1,0,1}
C.{0,1,2}
D.{-1,0,1,2}
(2)已知集合A={x|2<x<4},B={x|x<3或x>5},则A∩B=( )
A.{x|2<x<5}
B.{x|x<4或x>5}
C.{x|2<x<3}
D.{x|x<2或x>5}
【解析】 (1)易知M={-2,-1,0,1},N={-1,0,1,2,3},据交集定义可知M∩N={-1,0,1},故选B.
(2)将集合A、B画在数轴上,如图.
INCLUDEPICTURE
"../../../../C1-10.TIF"
\
MERGEFORMAT
由图可知A∩B={x|2
求两个集合的交集的方法
(1)对于元素个数有限的集合,逐个挑出两个集合的公共元素即可.
(2)对于元素个数无限的集合,一般借助数轴求交集,两个集合的交集等于两个集合在数轴上的相应图形所覆盖的公共范围,要注意端点值的取舍.
INCLUDEPICTURE"跟踪训练LLL.TIF"
INCLUDEPICTURE
"../../../../跟踪训练LLL.TIF"
\
MERGEFORMAT
1.若集合A={x|-2
INCLUDEPICTURE
"../../../../S1-16.TIF"
\
MERGEFORMAT
因为A={x|-2
}关系的Venn图如图所示,则阴影部分表示的集合中的元素有( )
INCLUDEPICTURE
"../../../../JN5.tif"
\
MERGEFORMAT
A.-1
B.0
C.1
D.3
解析:选CD.因为M={x|-1≤x≤3},N={x|x=2k-1,k∈N
},所以M∩N={1,3},故选CD.
探究点3 交集、并集性质的应用
INCLUDEPICTURE"例3LLL.TIF"
INCLUDEPICTURE
"../../../../例3LLL.TIF"
\
MERGEFORMAT
已知集合A={x|2
(1)若A∪B=B,求a的取值范围;
(2)若A∩B=?,求a的取值范围.
【解】 (1)因为A∪B=B,所以A?B,
INCLUDEPICTURE
"../../../../ab25.TIF"
\
MERGEFORMAT
观察数轴可知,所以≤a≤2.
(2)A∩B=?有两类情况:B在A的左边和B在A的右边,如图.
INCLUDEPICTURE
"../../../../ab26.TIF"
\
MERGEFORMAT
观察数轴可知,a≥4或3a≤2,又a>0,
所以0
INCLUDEPICTURE
"../../../../互动探究LLL.TIF"
\
MERGEFORMAT
(变条件)本例条件下,若A∩B={x|3
INCLUDEPICTURE
"../../../../ab27.TIF"
\
MERGEFORMAT
观察图形可知即a=3.
利用集合交集、并集的性质解题的方法
(1)在利用集合的交集、并集性质解题时,常常会遇到A∩B=A,A∪B=B等这类问题,解答时常借助于交、并集的定义及上节学习的集合间的关系去分析,如A∩B=A?A?B,A∪B=B?A?B等,解答时应灵活处理.
(2)当集合B?A时,如果集合A是一个确定的集合,而集合B不确定,运算时要考虑B=?的情况,切不可漏掉.
INCLUDEPICTURE"跟踪训练LLL.TIF"
INCLUDEPICTURE
"../../../../跟踪训练LLL.TIF"
\
MERGEFORMAT
1.已知M={1,2,a2-3a-1},N={-1,a,3},M∩N={3},则实数a的值为________.
解析:因为M∩N={3},
所以a2-3a-1=3,
解得a=-1或a=4.
又N={-1,a,3},所以a≠-1,
所以a=4.
答案:4
2.(一题两空)已知A={x|a
(1)若A∩B=A,则a的取值范围为________;
(2)若A∪B=R,则a的取值范围为________.
解析:(1)因为A∩B=A,所以A?B,
所以a≥5或a+8<-1,
即a≥5或a<-9.
(2)在数轴上标出集合A,B,如图.
INCLUDEPICTURE
"../../../../ab28.TIF"
\
MERGEFORMAT
要使A∪B=R,则
解得-3≤a<-1.
综上,可知a的取值范围为{a|-3≤a<-1}.
答案:(1)a≥5或a<-9 (2)-3≤a<-1
INCLUDEPICTURE"自测案当堂达标LLL.TIF"
INCLUDEPICTURE
"../../../../自测案当堂达标LLL.TIF"
\
MERGEFORMAT
1.设集合A={1,2},B={1,2,3},C={2,3,4},则(A∩B)∪C等于( )
A.{1,2,3}
B.{1,2,4}
C.{2,3,4}
D.{1,2,3,4}
解析:选D.因为A={1,2},B={1,2,3},
所以A∩B={1,2}.
又C={2,3,4},
所以(A∩B)∪C={1,2}∪{2,3,4}={1,2,3,4}.
2.(2020·平顶山高一检测)已知集合M={0,1,3},N={x|x=3a,a∈M},则M∪N=( )
A.{0}
B.{0,3}
C.{1,3,9}
D.{0,1,3,9}
解析:选D.因为M={0,1,3},
N={x|x=3a,a∈M}={0,3,9},
所以M∪N={0,1,3,9}.
3.已知A={(x,y)|x+y=3},B={(x,y)|x-y=1},则A∩B=( )
A.{2,1}
B.{x=2,y=1}
C.{(2,1)}
D.(2,1)
解析:选C.A∩B=
={(2,1)}.
4.已知集合A={x|3≤x≤9},B={x|2
(1)求A∪B;
(2)若B∩C=?,求实数a的取值范围.
解:(1)由A={x|3≤x≤9},B={x|2
故实数a的取值范围是{a|a≥5}.
INCLUDEPICTURE"应用案巩固提升LLL.TIF"
INCLUDEPICTURE
"../../../../应用案巩固提升LLL.TIF"
\
MERGEFORMAT
[A 基础达标]
1.设集合M={x|x2+2x=0,x∈R},N={x|x2-2x=0,x∈R},则M∪N等于( )
A.{0}
B.{0,2}
C.{-2,0}
D.{-2,0,2}
解析:选D.集合M={0,-2},N={0,2},故M∪N={-2,0,2},选D.
2.(2020·烟台高一检测)已知集合M={0,1,2},N={x|x=2a-1,a∈N
},则M∩N=( )
A.{0}
B.{1,2}
C.{1}
D.{2}
解析:选C.因为N={1,3,5,…},M={0,1,2},所以M∩N={1}.
3.已知集合P={x|x<3},Q={x|-1≤x≤4},则P∪Q=( )
A.{x|-1≤x<3}
B.{x|-1≤x≤4}
C.{x|x≤4}
D.{x|x≥-1}
解析:选C.在数轴上表示两个集合,如图.
INCLUDEPICTURE
"../../../../MF20.TIF"
\
MERGEFORMAT
易知P∪Q={x|x≤4}.
4.已知集合M={-1,1},则满足M∪N={-1,1,2}的集合N的个数是( )
A.1
B.2
C.3
D.4
解析:选D.依题意,得满足M∪N={-1,1,2}的集合N有{2},{-1,2},{1,2},{-1,1,2},共4个.
5.设集合A={x|-1≤x<2},B={x|x
B.a>-2
C.a>-1
D.-1
INCLUDEPICTURE
"../../../../S1-20.TIF"
\
MERGEFORMAT
6.(一题两空)若集合A={x|-1<x<5},B={x|x≤-1或x≥4},则A∪B=________;A∩B=________.
解析:如图所示,借助数轴可知:
INCLUDEPICTURE
"../../../../MF25.TIF"
\
MERGEFORMAT
A∪B=R,A∩B={x|4≤x<5}.
答案:R {x|4≤x<5}
7.若集合A={x|x≤2},B={x|x≥a},且满足A∩B={2},则实数a=________.
解析:当a>2时,A∩B=?;
当a<2时,A∩B={x|a≤x≤2};
当a=2时,A∩B={2}.
综上,a=2.
答案:2
8.已知集合A={3,2a},B={a,b}.若A∩B={2},则A∪B=________.
解析:因为A∩B={2},所以2a=2,即a=1.所以b=2,所以A={3,2},B={1,2},所以A∪B={1,2,3}.
答案:{1,2,3}
9.设A={x|x2+ax+12=0},B={x|x2+3x+2b=0},A∩B={2},C={2,-3}.
(1)求a,b的值及A,B;
(2)求(A∪B)∩C.
解:(1)因为A∩B={2},
所以4+2a+12=0,4+6+2b=0,
即a=-8,b=-5,
所以A={x|x2-8x+12=0}={2,6},
B={x|x2+3x-10=0}={2,-5}.
(2)因为A∪B={-5,2,6},C={2,-3},
所以(A∪B)∩C={2}.
10.已知集合A={x|x≥3},B={x|1≤x≤7},C={x|x≥a-1}.
(1)求A∩B,A∪B;
(2)若C∪A=A,求实数a的取值范围.
解:(1)因为A={x|x≥3},B={x|1≤x≤7},所以A∩B={x|3≤x≤7},A∪B={x|x≥1}.
(2)因为C∪A=A,A={x|x≥3},C={x|x≥a-1},
所以C?A,所以a-1≥3,即a≥4.
[B 能力提升]
11.(多选)已知集合A={x|x2-3x+2=0},B={x|ax-2=0},若A∩B=B,则实数a的值为( )
A.0
B.1
C.2
D.3
解析:选ABC.A={x|x2-3x+2=0}={1,2},
因为A∩B=B,所以B?A.
当B=?时,ax-2=0无解,所以a=0.
当B≠?时,x=,所以=1或=2,解得a=2或a=1.
所以实数a的值为0或1或2.故选ABC.
12.已知集合A={x|x2-px-2=0},B={x|x2+qx+r=0},且A∪B={-2,1,5},A∩B={-2},则p+q+r=________.
解析:因为A∩B={-2},
所以-2∈A且-2∈B,将x=-2代入x2-px-2=0,得p=-1,
所以A={1,-2},
因为A∪B={-2,1,5},A∩B={-2},
所以B={-2,5},
所以q=-[(-2)+5]=-3,r=(-2)×5=-10,
所以p+q+r=-14.
答案:-14
13.(一题两空)设集合A={2,-1,x2-x+1},B={2y,-4,x+4},C={-1,7},且A∩B=C,则x+y=________,A∪B=________.
解析:由A={2,-1,x2-x+1},B={2y,-4,x+4},C={-1,7}且A∩B=C,得
7∈A,7∈B且-1∈B,
所以在集合A中x2-x+1=7,
解得x=-2或3.
当x=-2时,在集合B中,x+4=2,
又2∈A,故2∈A∩B=C,
但2?C,故x=-2不合题意,舍去;
当x=3时,在集合B中,x+4=7,
故有2y=-1,解得y=-,
经检验满足A∩B=C.
综上知,所求x=3,y=-.所以x+y=.
此时A={2,-1,7},B={-1,-4,7},
故A∪B={-1,2,-4,7}.
答案: {-1,-4,2,7}
14.已知集合A={x|2a+1≤x≤3a-5},B={x|x<-1或x>16},分别根据下列条件求实数a的取值范围.
(1)A∩B=?;
(2)A?(A∩B).
解:(1)若A=?,则A∩B=?成立.此时2a+1>3a-5,
即a<6.
若A≠?,如图所示,
INCLUDEPICTURE
"../../../../S1-23.TIF"
\
MERGEFORMAT
则
解得6≤a≤7.综上,满足条件A∩B=?的实数a的取值范围是{a|a≤7}.
(2)因为A?(A∩B),所以A∩B=A,
即A?B.
显然A=?满足条件,此时a<6.
若A≠?,如图所示,
INCLUDEPICTURE
"../../../../S1-22.TIF"
\
MERGEFORMAT
则或
由解得a∈?;
由解得a>.
综上,满足条件A?(A∩B)的实数a的取值范围是{a|a<6或a>}.
[C 拓展探究]
15.某网店统计了连续三天售出商品的种类情况:第一天售出19种商品,第二天售出13种商品,第三天售出18种商品;前两天都售出的商品有3种,后两天都售出的商品有4种.则该网店
(1)第一天售出但第二天未售出的商品有多少种?
(2)这三天售出的商品最少有多少种?
解:设三天都售出的商品有x种,第一天售出,第二天未售出,且第三天售出的商品有y种,则三天售出商品的种类关系如图所示.
INCLUDEPICTURE
"../../../../HY1-1.TIF"
\
MERGEFORMAT
由图可知:(1)第一天售出但第二天未售出的商品有19-(3-x)-x=16(种).
(2)这三天售出的商品有(16-y)+y+x+(3-x)+(6+x)+(4-x)+(14-y)=43-y(种).
由于所以0≤y≤14.
所以(43-y)min=43-14=29.
HYPERLINK
"http://www.21cnjy.com/"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
