1.4 解直角三角形 一课一练(含解析)
文档属性
| 名称 | 1.4 解直角三角形 一课一练(含解析) |  | |
| 格式 | rar | ||
| 文件大小 | 396.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-08 11:28:50 | ||
图片预览




文档简介
初中数学北师大版九年级下学期 第一章 1.4 解直角三角形
一、单选题(共6题;共30分)
1.如图,AC是旗杆AB的一根拉线,拉直AC时,測得BC=3米,∠ACB=50°,则AB的高为( )
A.?3cos50°米????????????????????????B.?3tan50°米????????????????????????C.?米????????????????????????D.?米
【答案】 B
【解析】【解答】解:∵BC=3米,∠ACB=50°,tan∠ACB= ,
∴旗杆AB的高度为AB=BC×tan∠ACB=3tan50°(米),
故答案为:B.
【分析】由题意可知在Rt△ABC中,利用∠ACB=50°的正切函数进行分析解答.
2.如图,梯子AC的长为2.8米,则梯子顶端离地面的高度AD是(???? )
A.?米??????????????????????B.?米??????????????????????C.?sinα米??????????????????????D.?cosα米
【答案】 C
【解析】【解答】解:在Rt△ADC中,∠ACD=α,AC=2.8,
∴AD=ACsin∠ACD=2.8sinα=.
故答案为:C.
【分析】在Rt△ADC中,利用锐角三角函数的定义可求出AD的值。
3.如图,△ACB中,∠ACB=Rt∠,已知∠B=α,∠ADC=β,AB=a,则BD的长可表示为(?? )
A.?a?(cosα﹣cosβ)?????B.??????C.?acosα﹣ ?????D.?a?cosα﹣asinα?a?tanβ
【答案】 C
【解析】【解答】解:∵∠C=90°,∠B=α,∠ADC=β,AB=a,
∴cosB=cosα= = ,
则BC=a?cosα,
sinB=sinα= = ,
故AC=a?sinα,
则tanβ= ,
故DC= = ,
则BD=BC﹣DC=a?cosα﹣ .
故答案为:C.
【分析】由cosα= , 可得BC=a?cosα,由sinα= , 可得AC=a?sinα,由tanβ= , 可得DC= ?,利用BD=BC﹣DC即可求出结论.
4.△ABC中,∠C=90°,M是BC的三等分点,且MC=2MB,若sin∠ ,则sin∠MAC=(?? )
A.??????????????????????????????????????B.??????????????????????????????????????C.??????????????????????????????????????D.?
【答案】 C
【解析】【解答】解:过点M作MD⊥AB于点D,
设MD=x,BM=y,MC=2Y
在Rt△ADM中
?????
∴AM=5x,
在Rt△ACM中
在Rt△ABC中,
∵∠C=∠BDM=90°,∠B=∠B
∴△ABC∽△BDM
∴
∴5x2=2y2;
∴
∴.
故答案为:C.
【分析】过点M作MD⊥AB于点D,设MD=x,BM=y,MC=2y,利用解直角三角形求出AM,再利用勾股定理分别求出AC,AB,然后证明△ABC∽△BDM,利用相似三角形的对应边成比例,可得到5x2=2y2 , 然后利用解直角三角形求出(sin∠MAC)2的值,然后开方即可。
5.已知在Rt△ABC中,∠C=90°,AB=5,AC=3,则tanA的值(??? )
A.??????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?
【答案】 B
【解析】【解答】解:∵∠C=90°,AB=5,AC=3
∴BC=
∴
故答案为:B
【分析】本题考查正切三角函数,首先根据勾股定理求出BC,在根据正切三角函数的定义即可得到答案.
6.如图,在△ABC中,CA=CB=4,cosC= ,则sinB的值为(?? )
A.??????????????????????????????????B.??????????????????????????????????C.??????????????????????????????????D.?
【答案】 D
【解析】【解答】解:过点A作AD⊥BC,垂足为D,如图所示.
在Rt△ACD中,CD=CA?cosC=1,
∴AD= = ;
在Rt△ABD中,BD=CB﹣CD=3,AD= ,
∴AB= =2 ,
∴sinB= = .
故答案为:D.
【分析】过点A作AD⊥BC,垂足为D,如图所示.在Rt△ACD中,可得CD=CA?cosC=1,利用勾股定理求出AD=, 在Rt△ABD中,BD=CB﹣CD=3,利用勾股定理求出AB=2 , 由sinB= 即可求出结论.
二、填空题(共4题;共20分)
7.如图所示,在四边形ABCD中,∠B=90°,AB=2,CD=8.连接AC,AC⊥CD,若sin∠ACB= ,则AD长度是________.
【答案】 10
【解析】【解答】解:在Rt△ABC中,
∵AB=2,sin∠ACB= = ,
∴AC=2÷ =6.
在Rt△ADC中,
AD=
=
=10.
故答案为:10.
【分析】先根据正弦函数的定义,由sin∠ACB= 即可计算出AC,再在直角三角形ACD中,利用勾股定理求出AD.
8.在 中, , 为BC边上的高, ,则BC的长为________.
【答案】 7或5
【解析】【解答】解:如图,∵在Rt△ABD中, , ,
∴ ,即: ,
∴ ,
当D在BC之间时,BC=BD+CD=6+1=7;
当D在BC延长线上时,BC=BD-CD=6-1=5;
故答案为:7或5.
【分析】如图所示,分D在BC之间和BC延长线上两种情况考虑,先由 求出BD , 再求出BC的长.
9.如图,在大楼AB的楼顶B处测得另一栋楼CD底部C的俯角为60度,已知A、C两点间的距离为15米,那么大楼AB的高度为________米.(结果保留根号)
?
【答案】
【解析】【解答】解:根据题意,△ABC是直角三角形,∠A=90°,
∴ ,
∴ ;
∴大楼AB的高度为 米.
故答案为: .
【分析】由解直角三角形,得 ,即可求出AB的值.
10.如图,在Rt△ABC中,∠C=90°,点D为BC上一点,AD=BD,CD=1,AC= ,则∠B的度数为________ .
【答案】 30°
【解析】【解答】解:∵∠C=90°,CD=1,AC= ,
∴ ,
而AD=BD,
∴BD=2,
在Rt△ABC中,AC= ,BC=BD+CD=3,
∴tan∠B= ,
∴∠B=30°,
故答案为:30°.
【分析】根据勾股定理求得AD,再根据正切函数的定义及特殊锐角三角函数值即可得出答案.
三、解答题(共5题;共40分)
11.在Rt△ABC中,∠C=90°,AB=8,∠A=60°,解这个直角三角形.
【答案】 解:如图,
∵在Rt△ABC中,∠C=90°,∠A=60°,
∴∠B=90°﹣∠A=30°,
∵AB=8,
∴AC= AB=4,
由勾股定理得:BC= = =4 .
【解析】【分析】根据三角形内角和定理求出 ,根据含 角的直角三角形的性质求出 ,根据勾股定理求出 即可.
12.汾河孕育着世代的龙城子孙,而魅力汾河两岸那“新外滩”的称号,将太原人对汾河的爱表露无遗…贯穿太原的汾河,让桥,也成为太原的文化符号,让汾河两岸,也成为繁华的必争之地!北中环桥是世界上首座对称五拱反对称五跨非对称斜拉索桥,2013年开工建设,当年实现全线竣工通车.这座桥造型现代,宛如一条腾飞巨龙.小芸和小刚分别在桥面上的A,B处,准备测量其中一座弧形钢架拱梁顶部C处到桥面的距离AB=20m,小芸在A处测得∠CAB=36°,小刚在B处测得∠CBA=43°,求弧形钢架拱梁顶部C处到桥面的距离.(结果精确到0.1m)(参考数据sin36°≈0.59,cos36°≈0.81,tan36°≈0.73,sin43°≈0.68,cos43°≈0.73,tan43°≈0.93)
【答案】解:过点C作CD⊥AB于D.设CD=x,
在Rt△ADC中,tan36°= ,
∴AD= ,
在Rt△BCD中,tan∠B= ,
BD= ,
∴ =20,
解得x=8.179≈8.2m.
答:拱梁顶部C处到桥面的距离8.2m.
【解析】【分析】先作辅助线CD⊥AB交AB于点D,根据角度和三角函数的定义得到直角边之间的等量关系,假定CD长度为x,用含x的代数式表示AD和BD,最后根据AB的长度建立方程,从而得到答案。
13.如图,在 中, 的平分线 交 于点 .求 的长?
【答案】 解:在 中,
是 的平分线,
又
,
在 中, ,
.
故答案为: .
【解析】【分析】由 求出∠A=30°,进而得出∠ABC=60°,由BD是∠ABC的平分线得出∠CBD=30°,进而求出BC的长,最后用sin∠A即可求出AB的长.
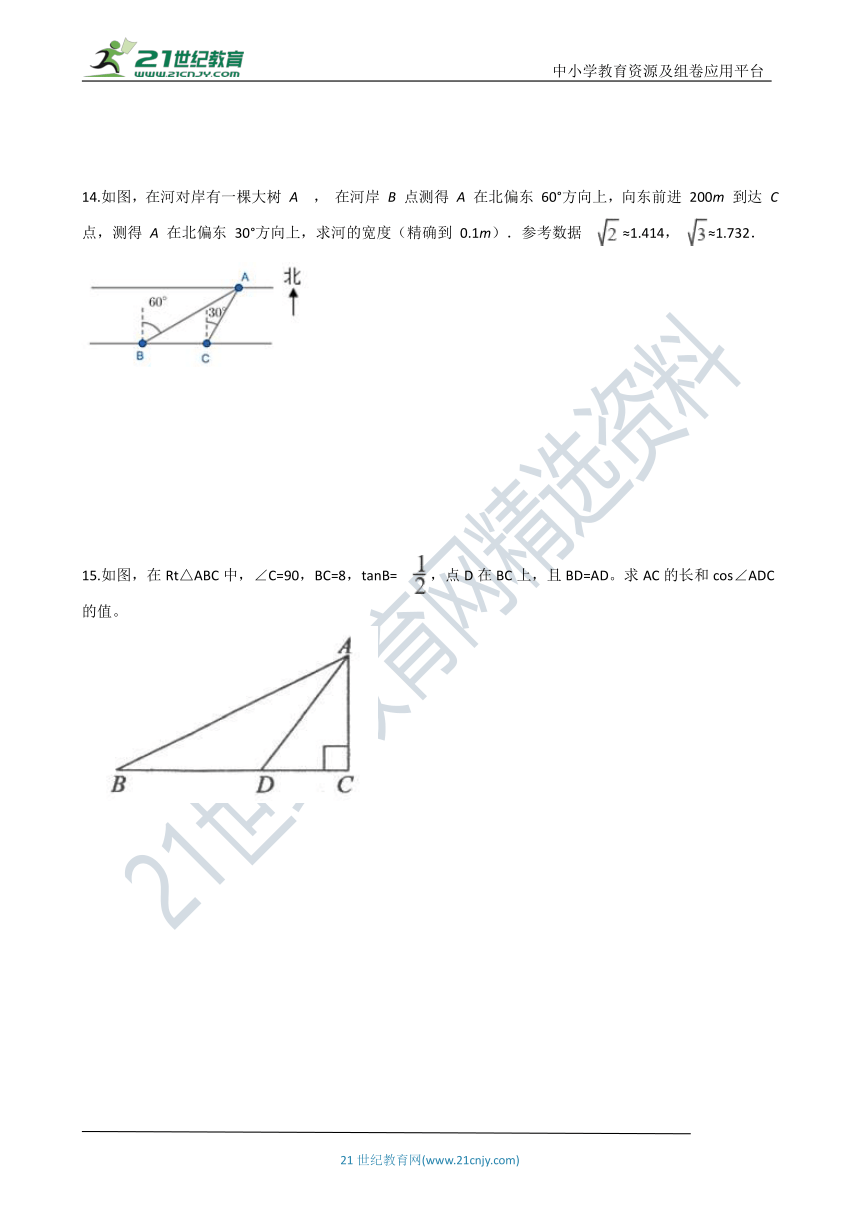
14.如图,在河对岸有一棵大树 A , 在河岸 B 点测得 A 在北偏东 60°方向上,向东前进 200m 到达 C 点,测得 A 在北偏东 30°方向上,求河的宽度(精确到 0.1m).参考数据 ?≈1.414, ≈1.732.
【答案】 解:过点A作AD⊥直线BC,垂足为点D,如图所示.
由题意可知:∠BAD=60°,∠CAD=30°,
在Rt△ABD中,tan∠BAD= ,
∴BD=AD?tan60°= ;
在Rt△ACD中,tan∠CAD= ,
∴CD=AD?tan30°= .
∴BC=BD?CD= - =200,
∴AD= .
∴河的宽度为173.2米.
【解析】【分析】过点A作AD⊥直线BC,垂足为点D,在Rt△ABD和Rt△ACD中,通过解直角三角形可求出BD,CD的长,结合BC=BD?CD=200,即可求出AD的长.
15.如图,在Rt△ABC中,∠C=90,BC=8,tanB= ,点D在BC上,且BD=AD。求AC的长和cos∠ADC的值。
【答案】 解:∵在Rt△ABC中,BC=8,tanB=
∴AC=4
设AD=x,则BD=x,CD=8-x
由勾股定理,得
(8-x)2+42=x2解得x=5
∴cos∠ADC=
【解析】【分析】利用锐角三角函数的定义,由tanB的值,就可求出AC的长,设AD=x,用含x的代数式表示出CD的长,再利用勾股定理建立关于x的方程,解方程求出x的值,然后利用锐角三角函数的定义求出cos∠ADC的值。
一、单选题(共6题;共30分)
1.如图,AC是旗杆AB的一根拉线,拉直AC时,測得BC=3米,∠ACB=50°,则AB的高为( )
A.?3cos50°米????????????????????????B.?3tan50°米????????????????????????C.?米????????????????????????D.?米
【答案】 B
【解析】【解答】解:∵BC=3米,∠ACB=50°,tan∠ACB= ,
∴旗杆AB的高度为AB=BC×tan∠ACB=3tan50°(米),
故答案为:B.
【分析】由题意可知在Rt△ABC中,利用∠ACB=50°的正切函数进行分析解答.
2.如图,梯子AC的长为2.8米,则梯子顶端离地面的高度AD是(???? )
A.?米??????????????????????B.?米??????????????????????C.?sinα米??????????????????????D.?cosα米
【答案】 C
【解析】【解答】解:在Rt△ADC中,∠ACD=α,AC=2.8,
∴AD=ACsin∠ACD=2.8sinα=.
故答案为:C.
【分析】在Rt△ADC中,利用锐角三角函数的定义可求出AD的值。
3.如图,△ACB中,∠ACB=Rt∠,已知∠B=α,∠ADC=β,AB=a,则BD的长可表示为(?? )
A.?a?(cosα﹣cosβ)?????B.??????C.?acosα﹣ ?????D.?a?cosα﹣asinα?a?tanβ
【答案】 C
【解析】【解答】解:∵∠C=90°,∠B=α,∠ADC=β,AB=a,
∴cosB=cosα= = ,
则BC=a?cosα,
sinB=sinα= = ,
故AC=a?sinα,
则tanβ= ,
故DC= = ,
则BD=BC﹣DC=a?cosα﹣ .
故答案为:C.
【分析】由cosα= , 可得BC=a?cosα,由sinα= , 可得AC=a?sinα,由tanβ= , 可得DC= ?,利用BD=BC﹣DC即可求出结论.
4.△ABC中,∠C=90°,M是BC的三等分点,且MC=2MB,若sin∠ ,则sin∠MAC=(?? )
A.??????????????????????????????????????B.??????????????????????????????????????C.??????????????????????????????????????D.?
【答案】 C
【解析】【解答】解:过点M作MD⊥AB于点D,
设MD=x,BM=y,MC=2Y
在Rt△ADM中
?????
∴AM=5x,
在Rt△ACM中
在Rt△ABC中,
∵∠C=∠BDM=90°,∠B=∠B
∴△ABC∽△BDM
∴
∴5x2=2y2;
∴
∴.
故答案为:C.
【分析】过点M作MD⊥AB于点D,设MD=x,BM=y,MC=2y,利用解直角三角形求出AM,再利用勾股定理分别求出AC,AB,然后证明△ABC∽△BDM,利用相似三角形的对应边成比例,可得到5x2=2y2 , 然后利用解直角三角形求出(sin∠MAC)2的值,然后开方即可。
5.已知在Rt△ABC中,∠C=90°,AB=5,AC=3,则tanA的值(??? )
A.??????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?
【答案】 B
【解析】【解答】解:∵∠C=90°,AB=5,AC=3
∴BC=
∴
故答案为:B
【分析】本题考查正切三角函数,首先根据勾股定理求出BC,在根据正切三角函数的定义即可得到答案.
6.如图,在△ABC中,CA=CB=4,cosC= ,则sinB的值为(?? )
A.??????????????????????????????????B.??????????????????????????????????C.??????????????????????????????????D.?
【答案】 D
【解析】【解答】解:过点A作AD⊥BC,垂足为D,如图所示.
在Rt△ACD中,CD=CA?cosC=1,
∴AD= = ;
在Rt△ABD中,BD=CB﹣CD=3,AD= ,
∴AB= =2 ,
∴sinB= = .
故答案为:D.
【分析】过点A作AD⊥BC,垂足为D,如图所示.在Rt△ACD中,可得CD=CA?cosC=1,利用勾股定理求出AD=, 在Rt△ABD中,BD=CB﹣CD=3,利用勾股定理求出AB=2 , 由sinB= 即可求出结论.
二、填空题(共4题;共20分)
7.如图所示,在四边形ABCD中,∠B=90°,AB=2,CD=8.连接AC,AC⊥CD,若sin∠ACB= ,则AD长度是________.
【答案】 10
【解析】【解答】解:在Rt△ABC中,
∵AB=2,sin∠ACB= = ,
∴AC=2÷ =6.
在Rt△ADC中,
AD=
=
=10.
故答案为:10.
【分析】先根据正弦函数的定义,由sin∠ACB= 即可计算出AC,再在直角三角形ACD中,利用勾股定理求出AD.
8.在 中, , 为BC边上的高, ,则BC的长为________.
【答案】 7或5
【解析】【解答】解:如图,∵在Rt△ABD中, , ,
∴ ,即: ,
∴ ,
当D在BC之间时,BC=BD+CD=6+1=7;
当D在BC延长线上时,BC=BD-CD=6-1=5;
故答案为:7或5.
【分析】如图所示,分D在BC之间和BC延长线上两种情况考虑,先由 求出BD , 再求出BC的长.
9.如图,在大楼AB的楼顶B处测得另一栋楼CD底部C的俯角为60度,已知A、C两点间的距离为15米,那么大楼AB的高度为________米.(结果保留根号)
?
【答案】
【解析】【解答】解:根据题意,△ABC是直角三角形,∠A=90°,
∴ ,
∴ ;
∴大楼AB的高度为 米.
故答案为: .
【分析】由解直角三角形,得 ,即可求出AB的值.
10.如图,在Rt△ABC中,∠C=90°,点D为BC上一点,AD=BD,CD=1,AC= ,则∠B的度数为________ .
【答案】 30°
【解析】【解答】解:∵∠C=90°,CD=1,AC= ,
∴ ,
而AD=BD,
∴BD=2,
在Rt△ABC中,AC= ,BC=BD+CD=3,
∴tan∠B= ,
∴∠B=30°,
故答案为:30°.
【分析】根据勾股定理求得AD,再根据正切函数的定义及特殊锐角三角函数值即可得出答案.
三、解答题(共5题;共40分)
11.在Rt△ABC中,∠C=90°,AB=8,∠A=60°,解这个直角三角形.
【答案】 解:如图,
∵在Rt△ABC中,∠C=90°,∠A=60°,
∴∠B=90°﹣∠A=30°,
∵AB=8,
∴AC= AB=4,
由勾股定理得:BC= = =4 .
【解析】【分析】根据三角形内角和定理求出 ,根据含 角的直角三角形的性质求出 ,根据勾股定理求出 即可.
12.汾河孕育着世代的龙城子孙,而魅力汾河两岸那“新外滩”的称号,将太原人对汾河的爱表露无遗…贯穿太原的汾河,让桥,也成为太原的文化符号,让汾河两岸,也成为繁华的必争之地!北中环桥是世界上首座对称五拱反对称五跨非对称斜拉索桥,2013年开工建设,当年实现全线竣工通车.这座桥造型现代,宛如一条腾飞巨龙.小芸和小刚分别在桥面上的A,B处,准备测量其中一座弧形钢架拱梁顶部C处到桥面的距离AB=20m,小芸在A处测得∠CAB=36°,小刚在B处测得∠CBA=43°,求弧形钢架拱梁顶部C处到桥面的距离.(结果精确到0.1m)(参考数据sin36°≈0.59,cos36°≈0.81,tan36°≈0.73,sin43°≈0.68,cos43°≈0.73,tan43°≈0.93)
【答案】解:过点C作CD⊥AB于D.设CD=x,
在Rt△ADC中,tan36°= ,
∴AD= ,
在Rt△BCD中,tan∠B= ,
BD= ,
∴ =20,
解得x=8.179≈8.2m.
答:拱梁顶部C处到桥面的距离8.2m.
【解析】【分析】先作辅助线CD⊥AB交AB于点D,根据角度和三角函数的定义得到直角边之间的等量关系,假定CD长度为x,用含x的代数式表示AD和BD,最后根据AB的长度建立方程,从而得到答案。
13.如图,在 中, 的平分线 交 于点 .求 的长?
【答案】 解:在 中,
是 的平分线,
又
,
在 中, ,
.
故答案为: .
【解析】【分析】由 求出∠A=30°,进而得出∠ABC=60°,由BD是∠ABC的平分线得出∠CBD=30°,进而求出BC的长,最后用sin∠A即可求出AB的长.
14.如图,在河对岸有一棵大树 A , 在河岸 B 点测得 A 在北偏东 60°方向上,向东前进 200m 到达 C 点,测得 A 在北偏东 30°方向上,求河的宽度(精确到 0.1m).参考数据 ?≈1.414, ≈1.732.
【答案】 解:过点A作AD⊥直线BC,垂足为点D,如图所示.
由题意可知:∠BAD=60°,∠CAD=30°,
在Rt△ABD中,tan∠BAD= ,
∴BD=AD?tan60°= ;
在Rt△ACD中,tan∠CAD= ,
∴CD=AD?tan30°= .
∴BC=BD?CD= - =200,
∴AD= .
∴河的宽度为173.2米.
【解析】【分析】过点A作AD⊥直线BC,垂足为点D,在Rt△ABD和Rt△ACD中,通过解直角三角形可求出BD,CD的长,结合BC=BD?CD=200,即可求出AD的长.
15.如图,在Rt△ABC中,∠C=90,BC=8,tanB= ,点D在BC上,且BD=AD。求AC的长和cos∠ADC的值。
【答案】 解:∵在Rt△ABC中,BC=8,tanB=
∴AC=4
设AD=x,则BD=x,CD=8-x
由勾股定理,得
(8-x)2+42=x2解得x=5
∴cos∠ADC=
【解析】【分析】利用锐角三角函数的定义,由tanB的值,就可求出AC的长,设AD=x,用含x的代数式表示出CD的长,再利用勾股定理建立关于x的方程,解方程求出x的值,然后利用锐角三角函数的定义求出cos∠ADC的值。
