1.1 锐角三角函数 一课一练(含解析)
文档属性
| 名称 | 1.1 锐角三角函数 一课一练(含解析) |

|
|
| 格式 | rar | ||
| 文件大小 | 254.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-08 11:15:44 | ||
图片预览




文档简介
初中数学北师大版九年级下学期 第一章 1.1 锐角三角函数
第一章 1.1 锐角三角函数
姓名:__________ 班级:__________考号:__________
一、单选题(共8题;共64分)
1.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论错误的是(? )
A.??????????????????????B.??????????????????????C.??????????????????????D.?
【答案】 C
【解析】【解答】解:在Rt△ABC中,∠BAC=90°,sinB= ,B符合题意
∵AD⊥BC,∴sinB= ,A符合题意
sinB=sin∠DAC= ,D符合题意
综上,只有C不符合题意
故答案为:C.
【分析】根据锐角三角函数的定义,即可解答.
2.如图,已知Rt△ABC中,∠C=90°,BC=3,AC=4,
则sinA的值为(?? ).
A.???????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
【答案】 C
【解析】【解答】∵∠C=90°,BC=3,AC=4
∴
∴
故答案为:C.
【分析】根据勾股定理求出AB,并根据正弦公式:sinA= 求解即可.
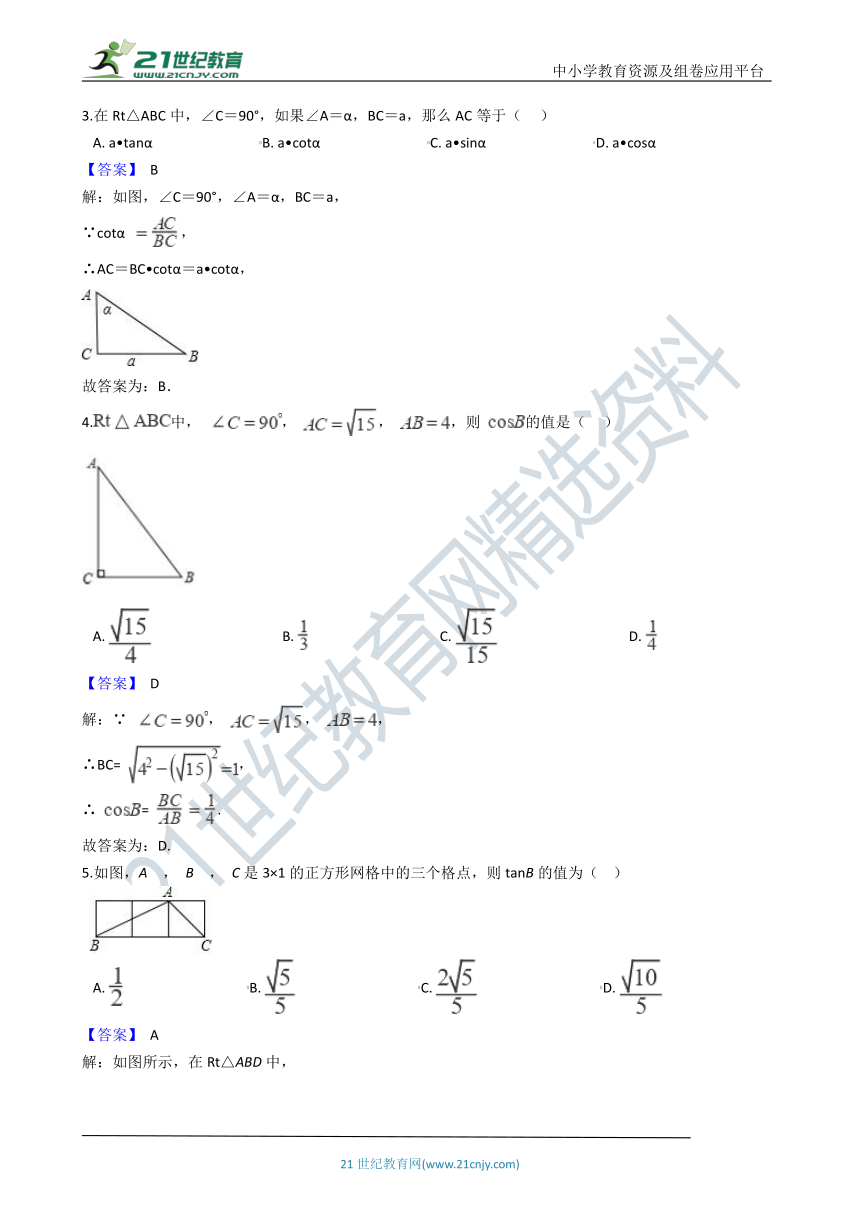
3.在Rt△ABC中,∠C=90°,如果∠A=α,BC=a,那么AC等于(??? )
A.?a?tanα???????????????????????????????B.?a?cotα???????????????????????????????C.?a?sinα???????????????????????????????D.?a?cosα
【答案】 B
【解析】【解答】如图,∠C=90°,∠A=α,BC=a,
∵cotα ,
∴AC=BC?cotα=a?cotα,
故答案为:B.
【分析】画出图形,根据锐角三角函数的定义求出即可.
4.中, , , ,则 的值是(??? )
A.??????????????????????????????????????B.??????????????????????????????????????C.??????????????????????????????????????D.?
【答案】 D
【解析】【解答】∵ , , ,
∴BC= ,
∴ = .
故答案为:D.
【分析】先根据勾股定理求出BC的长,然后根据余弦的定义求解即可.
5.如图,A , B , C是3×1的正方形网格中的三个格点,则tanB的值为(?? )
A.????????????????????????????????????B.????????????????????????????????????C.????????????????????????????????????D.?
【答案】 A
【解析】【解答】解:如图所示,在Rt△ABD中,
tanB= = .
故答案为:A .
【分析】根据锐角三角函数的定义,直接计算得结论.
6.如图,在△ABC中,∠A=90°,AB=3,BC=5,则cosB等于(??? )
A.???????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
【答案】 A
【解析】【解答】解:∵在△ABC中,∠A=90°,AB=3,BC=5,
∴cosB= = .
故答案为:A.
【分析】根据余弦函数的定义可知cosB= 即可直接得出答案.
7.在△ABC中,∠C=90°,AB=6,BC=2,则下列三角函数表示正确的是( )
A.?sinA=????????????????????????B.?cosB=2????????????????????????C.?tanA=????????????????????????D.?cosA=
【答案】 C
【解析】【解答】解:∵在△ABC中,∠C=90°,AB=6,BC=2,
∴,
∴sinA=, cosB=, tanA=, cosA=,
故选项A错误,选项B错误,选项C正确,选项D错误;
故选C.
【分析】根据在△ABC中,∠C=90°,AB=6,BC=2,可以求出AC的长,从而可以求出选项中几个角的锐角三角函数值,从而可以解答本题.
8.点(-sin60°,cos60°)关于y轴对称的点的坐标是(? )
A.?( , )?????????????B.?(- , )?????????????C.?(- ,- )?????????????D.?(- ,- )
【答案】 A
【解析】【解答】∵sin60°= ,cos60°= ,
∴(-sin60°,cos60°)=(- , ),
关于y轴对称点的坐标是( , ).
故答案为:A.
【分析】先利用特殊三角函数值,求出sin60°、cos60°的值,再利用坐标系中,任一点(x,y)关于y轴的对称点的坐标是(-x,y),即可求.
二、填空题(共7题;共56分)
9.如图,菱形ABCD的对角线AC,BD相交于点O.若tan∠BAC= ,AC=6,则BD的长是________.
【答案】 2
【解析】【解答】∵四边形ABCD是菱形,
∴AC⊥BD,AO=AC=3,BO=BD,
在Rt△AOB中,∵tan∠BAO=,
∴,
即:,
∴BO=1,
∴BD=2BO=2.
故答案为:2.
【分析】根据菱形的性质,得到AC⊥BD,AO=AC=3,BO=BD,再在Rt△AOB中,根据正切函数的定义,求出BO,进而求出BD的长.
10.在△ABC中∠C=90°,tanA= ,则cosB=________.
【答案】
【解析】【解答】解:∵在Rt△ABC中,∠C=90°,tanA= ,
设a= x , b=3x , 则c=2 x ,
∴cosB= .
故答案为: .
【分析】根据正切函数的定义,由tanA= ,可设a= x , b=3x , 根据勾股定理得出c=2 x , 进而即可根据余弦函数的定义求出 cosB 的值.
11.在 Rt△ABC中, , ,则 ________.
【答案】
【解析】【解答】解:在 中, ,
故答案为: .
【分析】根据sinA=计算即可.
12.如图,在Rt△ABC中,∠C=90°,AB=4,BC=1,则cosA的值是________.
【答案】
【解析】【解答】解:∵∠C=90°,AB=4,BC=1,
∴AC= = = ,
则cosA= = ,
故答案为: .
【分析】先利用勾股定理求得AC的长,然后根据锐角三角函数的定义求得cosA的值即可。
13.如图,在边长为1的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点O,则cos∠AOD=________.
【答案】
【解析】【解答】解:设右下角顶点为点F,取DF的中点E,连接BE,AE,如图所示.
∵点B为CF的中点,点E为DF的中点,
∴BE∥CD,
∴∠AOD=∠ABE.
在△ABE中,AB= ,AE=2 ,BE= ,
∵AB2=AE2+BE2 ,
∴∠AEB=90°,
∴cos∠ABE= =
∴cos∠AOD=
故答案为: .
【分析】设右下角顶点为点F,取DF的中点E,连接BE,AE,由点B为CF的中点、点E为DF的中点可得出BE∥CD,进而可得出∠AOD=∠ABE,在△ABE中,由AB2=AE2+BE2可得出∠AEB=90°,再利用余弦的定义即可求出cos∠ABE的值,此题得解.
14.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,tan∠BCD= ,AC=12,则BC=________。
【答案】
【解析】【解答】解:∵∠ACB=90°,CD⊥AB
∴∠A+∠B=90°,∠BCD+∠B=90°
∴∠A=∠BCD
∴tan∠A=tan∠BCD=
即
∴BC=AC=9.
【分析】先利用余角关系证出∠A=∠BCD,利用等角对应三角函数值相等得tan∠A=tan∠BCD,即, 则BC=AC=9,从而得解。
15.为解决停车难得问题,在如图一段长56米的路段开辟停车位,每个车位是长5米、宽2.2米的矩形,矩形的边与路的边缘成45°角,那么这个路段最多可以划出________个这样的停车位( )
【答案】 17
【解析】【解答】解:如图,
CE=2.2÷sin45°=2.2÷ ≈3.1米,
BC=(5-CE× )× ≈1.98米,
BE=BC+CE≈5.04,
EF=2.2÷sin45°=2.2÷ ≈3.1米,
(56-3.1-1.98)÷3.1+1
=50.92÷3.1+1
≈17(个).
故这个路段最多可以划出17个这样的停车位.
故答案为:17.
【分析】如图,根据三角函数可求BC,CE,由BE=BC+CE可求BE,再根据三角函数可求EF,再根据停车位的个数=(56-BE)÷EF+1,列式计算即可求解.
第一章 1.1 锐角三角函数
姓名:__________ 班级:__________考号:__________
一、单选题(共8题;共64分)
1.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论错误的是(? )
A.??????????????????????B.??????????????????????C.??????????????????????D.?
【答案】 C
【解析】【解答】解:在Rt△ABC中,∠BAC=90°,sinB= ,B符合题意
∵AD⊥BC,∴sinB= ,A符合题意
sinB=sin∠DAC= ,D符合题意
综上,只有C不符合题意
故答案为:C.
【分析】根据锐角三角函数的定义,即可解答.
2.如图,已知Rt△ABC中,∠C=90°,BC=3,AC=4,
则sinA的值为(?? ).
A.???????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
【答案】 C
【解析】【解答】∵∠C=90°,BC=3,AC=4
∴
∴
故答案为:C.
【分析】根据勾股定理求出AB,并根据正弦公式:sinA= 求解即可.
3.在Rt△ABC中,∠C=90°,如果∠A=α,BC=a,那么AC等于(??? )
A.?a?tanα???????????????????????????????B.?a?cotα???????????????????????????????C.?a?sinα???????????????????????????????D.?a?cosα
【答案】 B
【解析】【解答】如图,∠C=90°,∠A=α,BC=a,
∵cotα ,
∴AC=BC?cotα=a?cotα,
故答案为:B.
【分析】画出图形,根据锐角三角函数的定义求出即可.
4.中, , , ,则 的值是(??? )
A.??????????????????????????????????????B.??????????????????????????????????????C.??????????????????????????????????????D.?
【答案】 D
【解析】【解答】∵ , , ,
∴BC= ,
∴ = .
故答案为:D.
【分析】先根据勾股定理求出BC的长,然后根据余弦的定义求解即可.
5.如图,A , B , C是3×1的正方形网格中的三个格点,则tanB的值为(?? )
A.????????????????????????????????????B.????????????????????????????????????C.????????????????????????????????????D.?
【答案】 A
【解析】【解答】解:如图所示,在Rt△ABD中,
tanB= = .
故答案为:A .
【分析】根据锐角三角函数的定义,直接计算得结论.
6.如图,在△ABC中,∠A=90°,AB=3,BC=5,则cosB等于(??? )
A.???????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
【答案】 A
【解析】【解答】解:∵在△ABC中,∠A=90°,AB=3,BC=5,
∴cosB= = .
故答案为:A.
【分析】根据余弦函数的定义可知cosB= 即可直接得出答案.
7.在△ABC中,∠C=90°,AB=6,BC=2,则下列三角函数表示正确的是( )
A.?sinA=????????????????????????B.?cosB=2????????????????????????C.?tanA=????????????????????????D.?cosA=
【答案】 C
【解析】【解答】解:∵在△ABC中,∠C=90°,AB=6,BC=2,
∴,
∴sinA=, cosB=, tanA=, cosA=,
故选项A错误,选项B错误,选项C正确,选项D错误;
故选C.
【分析】根据在△ABC中,∠C=90°,AB=6,BC=2,可以求出AC的长,从而可以求出选项中几个角的锐角三角函数值,从而可以解答本题.
8.点(-sin60°,cos60°)关于y轴对称的点的坐标是(? )
A.?( , )?????????????B.?(- , )?????????????C.?(- ,- )?????????????D.?(- ,- )
【答案】 A
【解析】【解答】∵sin60°= ,cos60°= ,
∴(-sin60°,cos60°)=(- , ),
关于y轴对称点的坐标是( , ).
故答案为:A.
【分析】先利用特殊三角函数值,求出sin60°、cos60°的值,再利用坐标系中,任一点(x,y)关于y轴的对称点的坐标是(-x,y),即可求.
二、填空题(共7题;共56分)
9.如图,菱形ABCD的对角线AC,BD相交于点O.若tan∠BAC= ,AC=6,则BD的长是________.
【答案】 2
【解析】【解答】∵四边形ABCD是菱形,
∴AC⊥BD,AO=AC=3,BO=BD,
在Rt△AOB中,∵tan∠BAO=,
∴,
即:,
∴BO=1,
∴BD=2BO=2.
故答案为:2.
【分析】根据菱形的性质,得到AC⊥BD,AO=AC=3,BO=BD,再在Rt△AOB中,根据正切函数的定义,求出BO,进而求出BD的长.
10.在△ABC中∠C=90°,tanA= ,则cosB=________.
【答案】
【解析】【解答】解:∵在Rt△ABC中,∠C=90°,tanA= ,
设a= x , b=3x , 则c=2 x ,
∴cosB= .
故答案为: .
【分析】根据正切函数的定义,由tanA= ,可设a= x , b=3x , 根据勾股定理得出c=2 x , 进而即可根据余弦函数的定义求出 cosB 的值.
11.在 Rt△ABC中, , ,则 ________.
【答案】
【解析】【解答】解:在 中, ,
故答案为: .
【分析】根据sinA=计算即可.
12.如图,在Rt△ABC中,∠C=90°,AB=4,BC=1,则cosA的值是________.
【答案】
【解析】【解答】解:∵∠C=90°,AB=4,BC=1,
∴AC= = = ,
则cosA= = ,
故答案为: .
【分析】先利用勾股定理求得AC的长,然后根据锐角三角函数的定义求得cosA的值即可。
13.如图,在边长为1的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点O,则cos∠AOD=________.
【答案】
【解析】【解答】解:设右下角顶点为点F,取DF的中点E,连接BE,AE,如图所示.
∵点B为CF的中点,点E为DF的中点,
∴BE∥CD,
∴∠AOD=∠ABE.
在△ABE中,AB= ,AE=2 ,BE= ,
∵AB2=AE2+BE2 ,
∴∠AEB=90°,
∴cos∠ABE= =
∴cos∠AOD=
故答案为: .
【分析】设右下角顶点为点F,取DF的中点E,连接BE,AE,由点B为CF的中点、点E为DF的中点可得出BE∥CD,进而可得出∠AOD=∠ABE,在△ABE中,由AB2=AE2+BE2可得出∠AEB=90°,再利用余弦的定义即可求出cos∠ABE的值,此题得解.
14.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,tan∠BCD= ,AC=12,则BC=________。
【答案】
【解析】【解答】解:∵∠ACB=90°,CD⊥AB
∴∠A+∠B=90°,∠BCD+∠B=90°
∴∠A=∠BCD
∴tan∠A=tan∠BCD=
即
∴BC=AC=9.
【分析】先利用余角关系证出∠A=∠BCD,利用等角对应三角函数值相等得tan∠A=tan∠BCD,即, 则BC=AC=9,从而得解。
15.为解决停车难得问题,在如图一段长56米的路段开辟停车位,每个车位是长5米、宽2.2米的矩形,矩形的边与路的边缘成45°角,那么这个路段最多可以划出________个这样的停车位( )
【答案】 17
【解析】【解答】解:如图,
CE=2.2÷sin45°=2.2÷ ≈3.1米,
BC=(5-CE× )× ≈1.98米,
BE=BC+CE≈5.04,
EF=2.2÷sin45°=2.2÷ ≈3.1米,
(56-3.1-1.98)÷3.1+1
=50.92÷3.1+1
≈17(个).
故这个路段最多可以划出17个这样的停车位.
故答案为:17.
【分析】如图,根据三角函数可求BC,CE,由BE=BC+CE可求BE,再根据三角函数可求EF,再根据停车位的个数=(56-BE)÷EF+1,列式计算即可求解.
