1.5 三角函数的应用 一课一练(含解析)
文档属性
| 名称 | 1.5 三角函数的应用 一课一练(含解析) |
|
|
| 格式 | rar | ||
| 文件大小 | 498.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-08 00:00:00 | ||
图片预览


文档简介
初中数学北师大版九年级下学期 第一章 1.5 三角函数的应用
一、单选题(共6题;共30分)
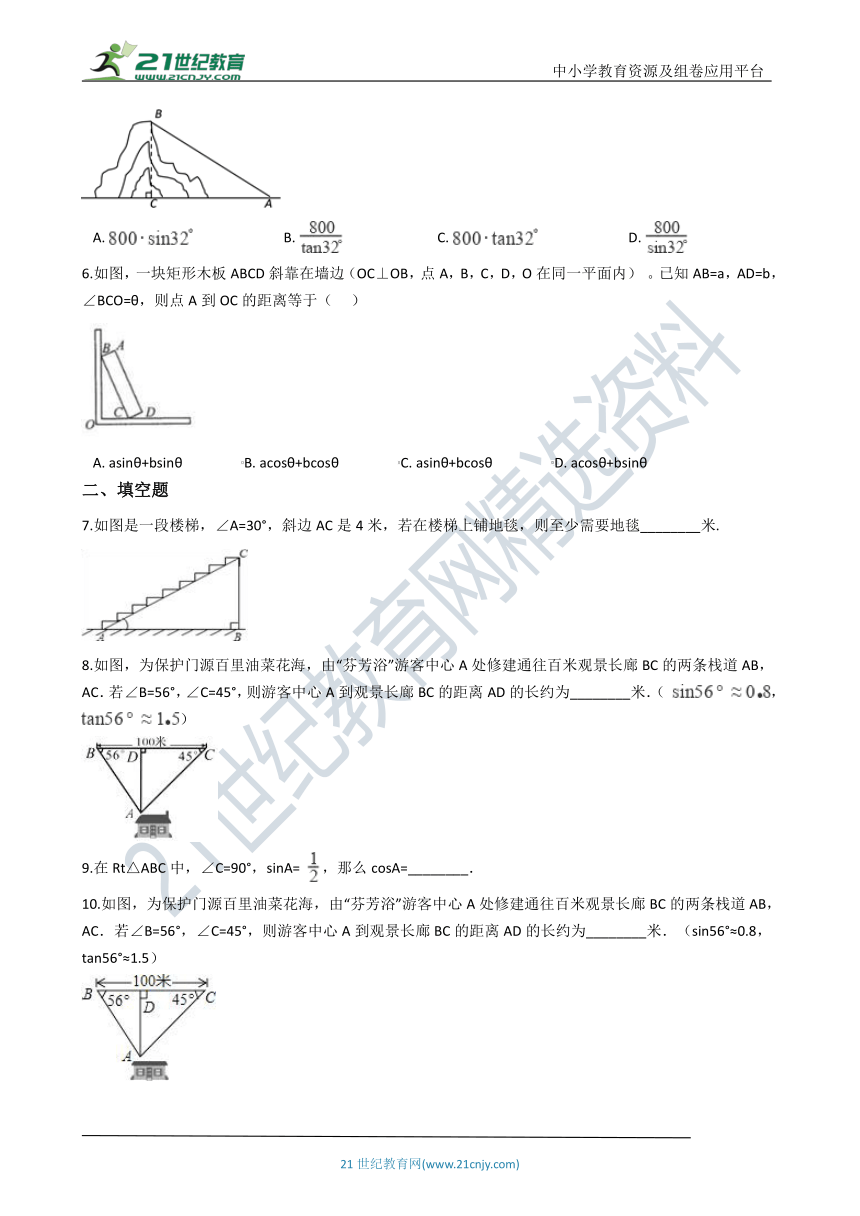
1.如图,一棵珍贵的树倾斜程度越来越厉害了.出于对它的保护,需要测量它的高度,现采取以下措施:在地面上选取一点C,测得∠BCA=37°,AC=28米,∠BAC=45°,则这棵树的高AB约为(参考数据:sin37°≈ ,tan37°≈ , ≈1.4)(??? )
A.?14米????????????????????????????????????B.?15米????????????????????????????????????C.?17米????????????????????????????????????D.?18米
【答案】 C
【解析】【解答】解:过点B作BD⊥AC于点D,设AD=x米,则CD=(28-x)米。
在Rt△ABD中,∠BAC=45°,∴BD=AD=x米
在Rt△CBD中,, 即
解得x=12
∴AB=x≈1.4×12=16.8≈17(米)
∴这棵树的高AB约为17米。
故答案为:C.
【分析】作BD⊥AC于点D,设AD=x米,则CD=(28-x)米。先在Rt△ABD中,由∠BAC=45°,得BD=AD=x米
在Rt△CBD中,利用三角函数的定义列出方程并求出的值,然后利用勾股定理即可求出AB。
2.如图,测得一商场自动扶梯的长为l,自动扶梯与地面所成的角为θ,则该自动扶梯到达的高度h为(???? )
A.?l·sinθ?????????????????????????????????B.??????????????????????????????????C.?l·cosθ?????????????????????????????????D.?
【答案】 A
【解析】【解答】sin=, ∴h=l·sin.
故答案为:A.
【分析】根据正弦函数的定义可得sin=, 从而求出结论.
3.斜坡的倾斜角为α,一辆汽车沿这个斜坡前进了500米,则它上升的高度是(??? )
A.?500sinα米?????????????????????????B.?米?????????????????????????C.?500cosα米?????????????????????????D.?米
【答案】 A
【解析】【解答】解:如图,
?,
?.
故答案为:A.
【分析】根据一个锐角的正弦等于对边比邻边可求解.
4.如图,在一块矩形ABCD区域内,正好划出5个全等的矩形停车位,其中EF=a米,FG=b米,∠AEF=30°,则AD等于(?? )
A.?( a+ b)米????????????????????????????????????B.?( a+ b)米
C.?(a+ b)米??????????????????????????????????????????D.?(a+ b)米
【答案】 A
【解析】【解答】解:如图,
∵EF=a米,∠A=90°,∠AEF=30°,
∴AF= EF= 米,∠AFE=60°,
∵∠EFG=90°,
∴∠MFG=30°,
∴PQ=NP=MN=FM= (米),
DQ=QK?cos30°= (米),
∴AD=AF+4FM+dq= a+4× + = a+ b(米),
故答案为:A.
【分析】在Rt△AEF中,通过解直角三角形求得AF,再在Rt△FMG和Rt△DQK中,通过解直角三角形求得FM,最后由AD=AF+4FM+DQ得结果.
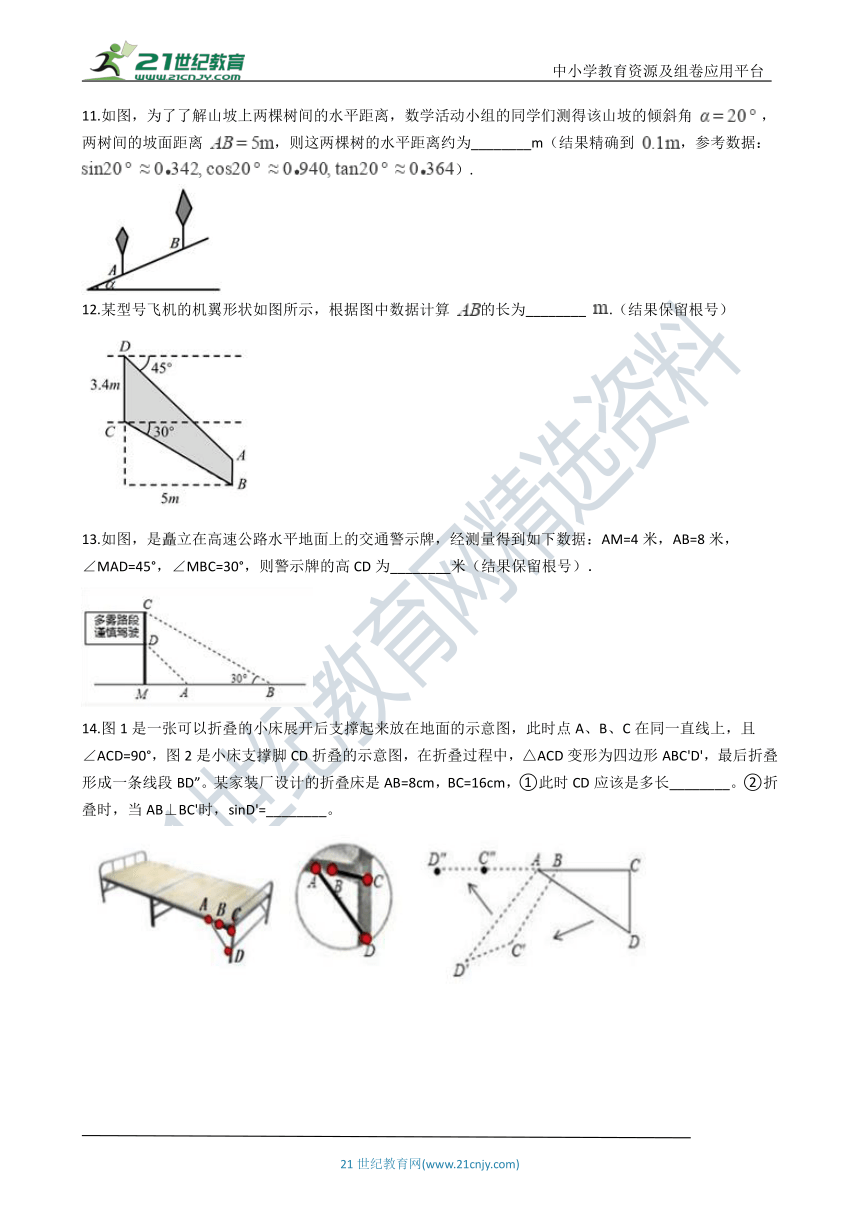
5.如图,在莲花山滑雪场滑雪,需从山脚下乘缆车上山,缆车索道与水平线所成的角为32°,缆车速度为每分钟50米,从山脚下A到达山顶B缆车需要16分钟,则山的高度BC为(???? )
A.???????????????????????????B.???????????????????????????C.???????????????????????????D.?
【答案】 A
【解析】【解答】如图,作BC⊥AC,垂足为C.
在Rt△ABC中,∠ACB=90°,∠BAC=32°,AB=50×16=800,sin∠BAC= ,∴BC=AB? sin∠BAC =800?sin32°(米).
故答案为:A.
【分析】作BC⊥AC,垂足为C.在Rt△ABC中,利用三角函数解答即可.
6.如图,一块矩形木板ABCD斜靠在墙边(OC⊥OB,点A,B,C,D,O在同一平面内) 。已知AB=a,AD=b,∠BCO=θ,则点A到OC的距离等于(??? )
A.?asinθ+bsinθ?????????????????B.?acosθ+bcosθ?????????????????C.?asinθ+bcosθ?????????????????D.?acosθ+bsinθ
【答案】 D
【解析】【解答】解:过点A作AF⊥PB于点F,AE⊥PD于点E,
∴∠AFP=∠AEP=∠P=90°,
∴四边形AFPE是矩形,?????????
∴AE=BP=BF+BP
∵四边形ABCD是矩形,
∴∠ABC=90°,AD=BC=b,
∴∠CBP+∠BCO=90°,∠ABF+∠CBP=90°
∴∠BCO=∠ABF=θ,
在Rt△BCP中
BP=BCsin∠BCO=bsinθ,
在Rt△AFB中,
BF=ABcos∠ABF=acosθ,
∴AE=acosθ+bsinθ,
∴点A到OC的距离等于acosθ+bsinθ.
故答案为:D
【分析】过点A作AF⊥PB于点F,AE⊥PD于点E,易证四边形AFPE是矩形,可得到AE=BP=BF+BP,再利用矩形的性质,可证得∠ABC=90°,AD=BC=b,利用余角的性质,可证得∠BCO=∠ABF=θ,在Rt△BCP和Rt△AFB中,利用解直角三角形求出BP,BF的长,然后求出BF的长,即可得到点A到OC的距离。
二、填空题(共8题;共45分)
7.如图是一段楼梯,∠A=30°,斜边AC是4米,若在楼梯上铺地毯,则至少需要地毯________米.
【答案】 (2+2 )
【解析】【解答】∵AC=4,∠A=30°,
∴BC=2,
∴AB=2 ,
所以需地毯(2+2 )米.
故答案为(2+2 ).
【分析】根据含30°角的直角三角形的性质可得BC=AC=2,利用勾股定理求出AB=2 ,从而求出需地毯长=AB+BC,代入数据计算即可.
8.如图,为保护门源百里油菜花海,由“芬芳浴”游客中心A处修建通往百米观景长廊BC的两条栈道AB,AC.若∠B=56°,∠C=45°,则游客中心A到观景长廊BC的距离AD的长约为________米.( , )
【答案】60
【解析】【解答】∵∠B=56°,∠C=45°,∠ADB=∠ADC=90°,BC=BD+CD=100米,∴BD= ,CD= ,∴ + =100,解得:AD≈60.故答案为:60.
【分析】在直角三角形ABD中,由∠ABD的正切可得tan∠ABD=,所以BD=,在直角三角形ACD中,有∠ACD的正切可得tan∠ACD=,CD=,而BD+CD=BC,所以+=100,解得AD≈60.
9.在Rt△ABC中,∠C=90°,sinA= ,那么cosA=________.
【答案】
【解析】【解答】如图所示:
∵Rt△ABC中,∠C=90°,∴sinA= ,
∵sinA= ,∴c=2a,∴b= ?,
∴cosA= ,
故答案为: .
【分析】利用角直角三角开的知识进行计算即可。
10.如图,为保护门源百里油菜花海,由“芬芳浴”游客中心A处修建通往百米观景长廊BC的两条栈道AB,AC.若∠B=56°,∠C=45°,则游客中心A到观景长廊BC的距离AD的长约为________米.(sin56°≈0.8,tan56°≈1.5)
【答案】 60
【解析】【解答】解:∵∠B=56°,∠C=45°,∠ADB=∠ADC=90°,BC=BD+CD=100米,
∴BD= ,CD= ,
∴ + =100,
解得,AD≈60,
故答案为:60.
【分析】根据题意和图形可以分别表示出AD和CD的长,从而可以求得AD的长,本题得以解决.本题考查解直角三角形的应用,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.
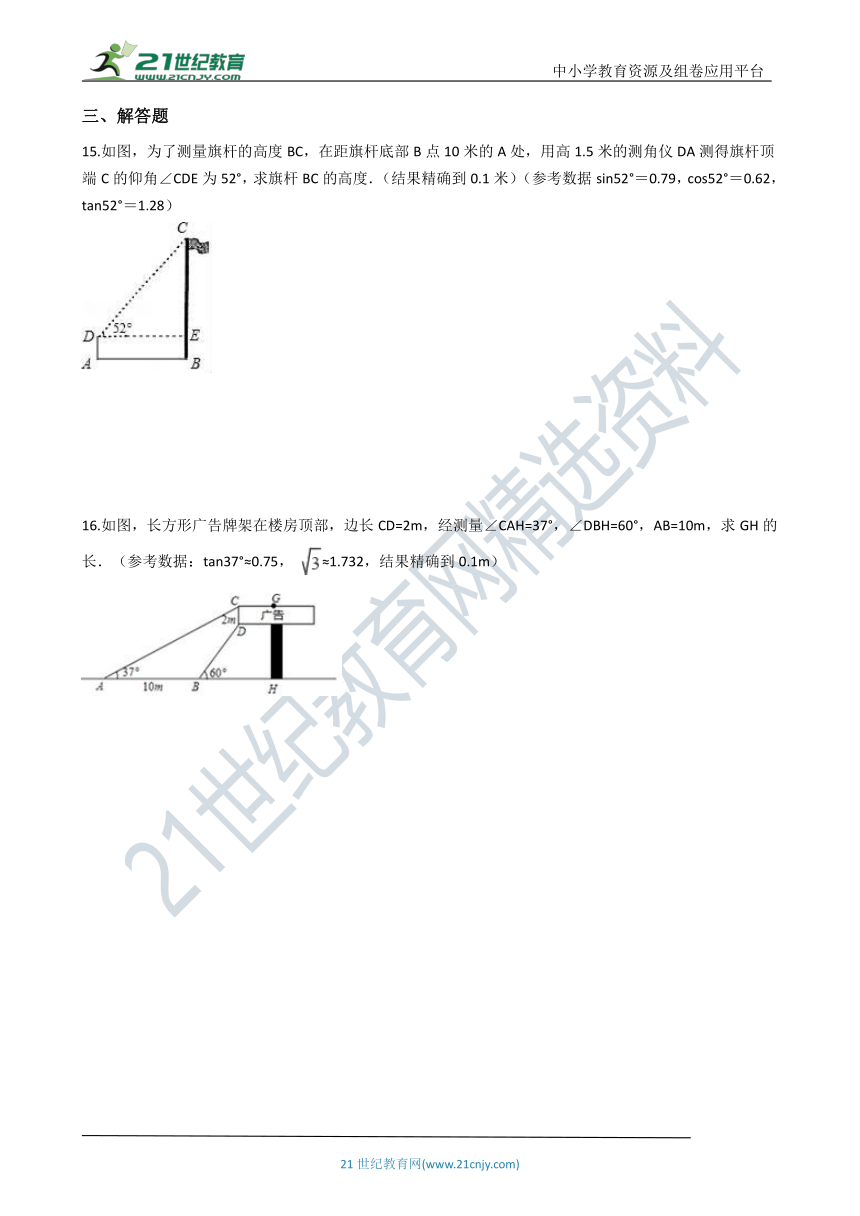
11.如图,为了了解山坡上两棵树间的水平距离,数学活动小组的同学们测得该山坡的倾斜角 ,两树间的坡面距离 ,则这两棵树的水平距离约为________m(结果精确到 ,参考数据: ).
【答案】 4.7
【解析】【解答】解:如图所示,过点A作AC平行于水平面,过点B作BC⊥AC于点C,则AC为所求,
由题意可知:∠BAC=α=20°,AB=5,
则 ,
即 ,
故答案为:4.7.
【分析】如图所示作出辅助线,得到∠BAC=α=20°,AB=5,再利用余弦的定义,得到 即可解答.
12.某型号飞机的机翼形状如图所示,根据图中数据计算 的长为________ .(结果保留根号)
【答案】
【解析】【解答】解:如图,过A作 ,交DF于点E,则四边形ABFE是矩形
由图中数据可知, , , ,
在 中, ,即
解得
是等腰三角形
则 的长为
故答案为: .
【分析】如图,先在 中,解直角三角形可求出CF的长,再根据等腰直角三角形的判定与性质可得DE的长,从而可得CE的长,然后根据线段的和差即可得.
13.如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为________米(结果保留根号).
【答案】 一4
【解析】【解答】因为∠MAD=45°, AM=4,所以MD=4,
因为AB=8,所以MB=12,
因为∠MBC=30°,所以CM=MBtan30°=4 .
所以CD=4 -4.
【分析】分析:利用特殊三角函数值,解直角三角形,AM=MD,再用正切函数,利用MB求CM,作差可求DC.
14.图1是一张可以折叠的小床展开后支撑起来放在地面的示意图,此时点A、B、C在同一直线上,且∠ACD=90°,图2是小床支撑脚CD折叠的示意图,在折叠过程中,△ACD变形为四边形ABC'D',最后折叠形成一条线段BD”。某家装厂设计的折叠床是AB=8cm,BC=16cm,①此时CD应该是多长________。②折叠时,当AB⊥BC'时,sinD'=________。
【答案】 32;
【解析】【解答】解:(1)根据题意可知:BC=BC"=16cm,AD=AD”,CD=C"D",∴AC"=BC"-AB=8cm,设CD=C"D"=x,则AD=AD”=AC"+C"D"=x+8(cm),在Rt△ACD中,由勾股定理得AC2+CD2=AD2,即242+x2=(x+8)2,解得x=32,即CD=32.
故答案为:32.
(2)如图:过点C'作C'E⊥AD',连接AC',
由题意可知:BC'=BC=16,CD=C'D'=32,AD'=AD=40,
在Rt△ABC'中,根据勾股定理得,
设D'E=y,则AE=40-y,
在Rt△AEC中,C'E2=C'A2-AE2=320-(40-x)2,
Rt△C'D'E中,C'E2=C'D'2-D'E2=322-x2,∴320-(40-x)2=322-x2,解得:x=,
∴在Rt△C'D'E中,C'E=,∴ sinD'= .
故答案为:.
【分析】(1)根据题意可知:BC=BC"=16cm,AD=AD”,CD=C"D",∴AC"=BC"-AB=8cm,设CD=C"D"=x,则AD=AD”=AC"+C"D"=x+8(cm),在Rt△ACD中,利用勾股定理建立方程,求解即可;
(2)过点C'作C'E⊥AD',连接AC',由题意可知:BC'=BC=16,CD=C'D'=32,AD'=AD=40,
在Rt△ABC'中,根据勾股定理算出AC',设D'E=y,则AE=40-y,在Rt△AEC中,利用勾股定理得C'E2=C'A2-AE2=320-(40-x)2,Rt△C'D'E中,利用勾股定理得C'E2=C'D'2-D'E2=322-x2,从而建立方程,求解即可得出x的值,进而在Rt△C'D'E中利用勾股定理求出C'E,从而根据正弦函数的定义即可求出 sinD' 的值.
三、解答题(共2题;共20分)
15.如图,为了测量旗杆的高度BC,在距旗杆底部B点10米的A处,用高1.5米的测角仪DA测得旗杆顶端C的仰角∠CDE为52°,求旗杆BC的高度.(结果精确到0.1米)(参考数据sin52°=0.79,cos52°=0.62,tan52°=1.28)
【答案】 解:过点D作DE⊥BC交BC于E,
在△CDE中,有CE=tan52°×DE=1.28×10≈12.8,
故BC=BE+CE=1.5+12.8≈14.3,
答:旗杆的高度为14.3米.
【解析】【分析】首先分析图形:根据题意构造直角三角形△ADE,解其可得DE的长,进而借助BC=EC+EB可解即可求出答案.
16.如图,长方形广告牌架在楼房顶部,边长CD=2m,经测量∠CAH=37°,∠DBH=60°,AB=10m,求GH的长.
(参考数据:tan37°≈0.75, ≈1.732,结果精确到0.1m)
【答案】 解:延长CD交AH于点E,如图所示:
根据题意得:CE⊥AH,设DE=xm,则CE=(x+2)m,
在Rt△AEC和Rt△BED中,tan37°= ,tan60°= ,
∴AE= ,BE= ,
∵AE-BE=AB,
∴ - =10,即 =10,
解得:x≈5.8,
∴DE=5.8m,
∴GH=CE=CD+DE=2m+5.8m=7.8m.
答:GH的长为7.8m.
【解析】【分析】延长CD交AH于点E,设DE=x,用含x的代数式表示出CE的长,再在Rt△AEC和Rt△BED中,利用解直角三角形表示出AE,BE的长,然后根据AE-BE=AB,建立关于x的方程,解方程求出x的值,继而可求出GH的长。
一、单选题(共6题;共30分)
1.如图,一棵珍贵的树倾斜程度越来越厉害了.出于对它的保护,需要测量它的高度,现采取以下措施:在地面上选取一点C,测得∠BCA=37°,AC=28米,∠BAC=45°,则这棵树的高AB约为(参考数据:sin37°≈ ,tan37°≈ , ≈1.4)(??? )
A.?14米????????????????????????????????????B.?15米????????????????????????????????????C.?17米????????????????????????????????????D.?18米
【答案】 C
【解析】【解答】解:过点B作BD⊥AC于点D,设AD=x米,则CD=(28-x)米。
在Rt△ABD中,∠BAC=45°,∴BD=AD=x米
在Rt△CBD中,, 即
解得x=12
∴AB=x≈1.4×12=16.8≈17(米)
∴这棵树的高AB约为17米。
故答案为:C.
【分析】作BD⊥AC于点D,设AD=x米,则CD=(28-x)米。先在Rt△ABD中,由∠BAC=45°,得BD=AD=x米
在Rt△CBD中,利用三角函数的定义列出方程并求出的值,然后利用勾股定理即可求出AB。
2.如图,测得一商场自动扶梯的长为l,自动扶梯与地面所成的角为θ,则该自动扶梯到达的高度h为(???? )
A.?l·sinθ?????????????????????????????????B.??????????????????????????????????C.?l·cosθ?????????????????????????????????D.?
【答案】 A
【解析】【解答】sin=, ∴h=l·sin.
故答案为:A.
【分析】根据正弦函数的定义可得sin=, 从而求出结论.
3.斜坡的倾斜角为α,一辆汽车沿这个斜坡前进了500米,则它上升的高度是(??? )
A.?500sinα米?????????????????????????B.?米?????????????????????????C.?500cosα米?????????????????????????D.?米
【答案】 A
【解析】【解答】解:如图,
?,
?.
故答案为:A.
【分析】根据一个锐角的正弦等于对边比邻边可求解.
4.如图,在一块矩形ABCD区域内,正好划出5个全等的矩形停车位,其中EF=a米,FG=b米,∠AEF=30°,则AD等于(?? )
A.?( a+ b)米????????????????????????????????????B.?( a+ b)米
C.?(a+ b)米??????????????????????????????????????????D.?(a+ b)米
【答案】 A
【解析】【解答】解:如图,
∵EF=a米,∠A=90°,∠AEF=30°,
∴AF= EF= 米,∠AFE=60°,
∵∠EFG=90°,
∴∠MFG=30°,
∴PQ=NP=MN=FM= (米),
DQ=QK?cos30°= (米),
∴AD=AF+4FM+dq= a+4× + = a+ b(米),
故答案为:A.
【分析】在Rt△AEF中,通过解直角三角形求得AF,再在Rt△FMG和Rt△DQK中,通过解直角三角形求得FM,最后由AD=AF+4FM+DQ得结果.
5.如图,在莲花山滑雪场滑雪,需从山脚下乘缆车上山,缆车索道与水平线所成的角为32°,缆车速度为每分钟50米,从山脚下A到达山顶B缆车需要16分钟,则山的高度BC为(???? )
A.???????????????????????????B.???????????????????????????C.???????????????????????????D.?
【答案】 A
【解析】【解答】如图,作BC⊥AC,垂足为C.
在Rt△ABC中,∠ACB=90°,∠BAC=32°,AB=50×16=800,sin∠BAC= ,∴BC=AB? sin∠BAC =800?sin32°(米).
故答案为:A.
【分析】作BC⊥AC,垂足为C.在Rt△ABC中,利用三角函数解答即可.
6.如图,一块矩形木板ABCD斜靠在墙边(OC⊥OB,点A,B,C,D,O在同一平面内) 。已知AB=a,AD=b,∠BCO=θ,则点A到OC的距离等于(??? )
A.?asinθ+bsinθ?????????????????B.?acosθ+bcosθ?????????????????C.?asinθ+bcosθ?????????????????D.?acosθ+bsinθ
【答案】 D
【解析】【解答】解:过点A作AF⊥PB于点F,AE⊥PD于点E,
∴∠AFP=∠AEP=∠P=90°,
∴四边形AFPE是矩形,?????????
∴AE=BP=BF+BP
∵四边形ABCD是矩形,
∴∠ABC=90°,AD=BC=b,
∴∠CBP+∠BCO=90°,∠ABF+∠CBP=90°
∴∠BCO=∠ABF=θ,
在Rt△BCP中
BP=BCsin∠BCO=bsinθ,
在Rt△AFB中,
BF=ABcos∠ABF=acosθ,
∴AE=acosθ+bsinθ,
∴点A到OC的距离等于acosθ+bsinθ.
故答案为:D
【分析】过点A作AF⊥PB于点F,AE⊥PD于点E,易证四边形AFPE是矩形,可得到AE=BP=BF+BP,再利用矩形的性质,可证得∠ABC=90°,AD=BC=b,利用余角的性质,可证得∠BCO=∠ABF=θ,在Rt△BCP和Rt△AFB中,利用解直角三角形求出BP,BF的长,然后求出BF的长,即可得到点A到OC的距离。
二、填空题(共8题;共45分)
7.如图是一段楼梯,∠A=30°,斜边AC是4米,若在楼梯上铺地毯,则至少需要地毯________米.
【答案】 (2+2 )
【解析】【解答】∵AC=4,∠A=30°,
∴BC=2,
∴AB=2 ,
所以需地毯(2+2 )米.
故答案为(2+2 ).
【分析】根据含30°角的直角三角形的性质可得BC=AC=2,利用勾股定理求出AB=2 ,从而求出需地毯长=AB+BC,代入数据计算即可.
8.如图,为保护门源百里油菜花海,由“芬芳浴”游客中心A处修建通往百米观景长廊BC的两条栈道AB,AC.若∠B=56°,∠C=45°,则游客中心A到观景长廊BC的距离AD的长约为________米.( , )
【答案】60
【解析】【解答】∵∠B=56°,∠C=45°,∠ADB=∠ADC=90°,BC=BD+CD=100米,∴BD= ,CD= ,∴ + =100,解得:AD≈60.故答案为:60.
【分析】在直角三角形ABD中,由∠ABD的正切可得tan∠ABD=,所以BD=,在直角三角形ACD中,有∠ACD的正切可得tan∠ACD=,CD=,而BD+CD=BC,所以+=100,解得AD≈60.
9.在Rt△ABC中,∠C=90°,sinA= ,那么cosA=________.
【答案】
【解析】【解答】如图所示:
∵Rt△ABC中,∠C=90°,∴sinA= ,
∵sinA= ,∴c=2a,∴b= ?,
∴cosA= ,
故答案为: .
【分析】利用角直角三角开的知识进行计算即可。
10.如图,为保护门源百里油菜花海,由“芬芳浴”游客中心A处修建通往百米观景长廊BC的两条栈道AB,AC.若∠B=56°,∠C=45°,则游客中心A到观景长廊BC的距离AD的长约为________米.(sin56°≈0.8,tan56°≈1.5)
【答案】 60
【解析】【解答】解:∵∠B=56°,∠C=45°,∠ADB=∠ADC=90°,BC=BD+CD=100米,
∴BD= ,CD= ,
∴ + =100,
解得,AD≈60,
故答案为:60.
【分析】根据题意和图形可以分别表示出AD和CD的长,从而可以求得AD的长,本题得以解决.本题考查解直角三角形的应用,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.
11.如图,为了了解山坡上两棵树间的水平距离,数学活动小组的同学们测得该山坡的倾斜角 ,两树间的坡面距离 ,则这两棵树的水平距离约为________m(结果精确到 ,参考数据: ).
【答案】 4.7
【解析】【解答】解:如图所示,过点A作AC平行于水平面,过点B作BC⊥AC于点C,则AC为所求,
由题意可知:∠BAC=α=20°,AB=5,
则 ,
即 ,
故答案为:4.7.
【分析】如图所示作出辅助线,得到∠BAC=α=20°,AB=5,再利用余弦的定义,得到 即可解答.
12.某型号飞机的机翼形状如图所示,根据图中数据计算 的长为________ .(结果保留根号)
【答案】
【解析】【解答】解:如图,过A作 ,交DF于点E,则四边形ABFE是矩形
由图中数据可知, , , ,
在 中, ,即
解得
是等腰三角形
则 的长为
故答案为: .
【分析】如图,先在 中,解直角三角形可求出CF的长,再根据等腰直角三角形的判定与性质可得DE的长,从而可得CE的长,然后根据线段的和差即可得.
13.如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为________米(结果保留根号).
【答案】 一4
【解析】【解答】因为∠MAD=45°, AM=4,所以MD=4,
因为AB=8,所以MB=12,
因为∠MBC=30°,所以CM=MBtan30°=4 .
所以CD=4 -4.
【分析】分析:利用特殊三角函数值,解直角三角形,AM=MD,再用正切函数,利用MB求CM,作差可求DC.
14.图1是一张可以折叠的小床展开后支撑起来放在地面的示意图,此时点A、B、C在同一直线上,且∠ACD=90°,图2是小床支撑脚CD折叠的示意图,在折叠过程中,△ACD变形为四边形ABC'D',最后折叠形成一条线段BD”。某家装厂设计的折叠床是AB=8cm,BC=16cm,①此时CD应该是多长________。②折叠时,当AB⊥BC'时,sinD'=________。
【答案】 32;
【解析】【解答】解:(1)根据题意可知:BC=BC"=16cm,AD=AD”,CD=C"D",∴AC"=BC"-AB=8cm,设CD=C"D"=x,则AD=AD”=AC"+C"D"=x+8(cm),在Rt△ACD中,由勾股定理得AC2+CD2=AD2,即242+x2=(x+8)2,解得x=32,即CD=32.
故答案为:32.
(2)如图:过点C'作C'E⊥AD',连接AC',
由题意可知:BC'=BC=16,CD=C'D'=32,AD'=AD=40,
在Rt△ABC'中,根据勾股定理得,
设D'E=y,则AE=40-y,
在Rt△AEC中,C'E2=C'A2-AE2=320-(40-x)2,
Rt△C'D'E中,C'E2=C'D'2-D'E2=322-x2,∴320-(40-x)2=322-x2,解得:x=,
∴在Rt△C'D'E中,C'E=,∴ sinD'= .
故答案为:.
【分析】(1)根据题意可知:BC=BC"=16cm,AD=AD”,CD=C"D",∴AC"=BC"-AB=8cm,设CD=C"D"=x,则AD=AD”=AC"+C"D"=x+8(cm),在Rt△ACD中,利用勾股定理建立方程,求解即可;
(2)过点C'作C'E⊥AD',连接AC',由题意可知:BC'=BC=16,CD=C'D'=32,AD'=AD=40,
在Rt△ABC'中,根据勾股定理算出AC',设D'E=y,则AE=40-y,在Rt△AEC中,利用勾股定理得C'E2=C'A2-AE2=320-(40-x)2,Rt△C'D'E中,利用勾股定理得C'E2=C'D'2-D'E2=322-x2,从而建立方程,求解即可得出x的值,进而在Rt△C'D'E中利用勾股定理求出C'E,从而根据正弦函数的定义即可求出 sinD' 的值.
三、解答题(共2题;共20分)
15.如图,为了测量旗杆的高度BC,在距旗杆底部B点10米的A处,用高1.5米的测角仪DA测得旗杆顶端C的仰角∠CDE为52°,求旗杆BC的高度.(结果精确到0.1米)(参考数据sin52°=0.79,cos52°=0.62,tan52°=1.28)
【答案】 解:过点D作DE⊥BC交BC于E,
在△CDE中,有CE=tan52°×DE=1.28×10≈12.8,
故BC=BE+CE=1.5+12.8≈14.3,
答:旗杆的高度为14.3米.
【解析】【分析】首先分析图形:根据题意构造直角三角形△ADE,解其可得DE的长,进而借助BC=EC+EB可解即可求出答案.
16.如图,长方形广告牌架在楼房顶部,边长CD=2m,经测量∠CAH=37°,∠DBH=60°,AB=10m,求GH的长.
(参考数据:tan37°≈0.75, ≈1.732,结果精确到0.1m)
【答案】 解:延长CD交AH于点E,如图所示:
根据题意得:CE⊥AH,设DE=xm,则CE=(x+2)m,
在Rt△AEC和Rt△BED中,tan37°= ,tan60°= ,
∴AE= ,BE= ,
∵AE-BE=AB,
∴ - =10,即 =10,
解得:x≈5.8,
∴DE=5.8m,
∴GH=CE=CD+DE=2m+5.8m=7.8m.
答:GH的长为7.8m.
【解析】【分析】延长CD交AH于点E,设DE=x,用含x的代数式表示出CE的长,再在Rt△AEC和Rt△BED中,利用解直角三角形表示出AE,BE的长,然后根据AE-BE=AB,建立关于x的方程,解方程求出x的值,继而可求出GH的长。
