1.6 利用三角函数测高 一课一练(含解析)
文档属性
| 名称 | 1.6 利用三角函数测高 一课一练(含解析) |

|
|
| 格式 | rar | ||
| 文件大小 | 469.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-08 00:00:00 | ||
图片预览




文档简介
初中数学北师大版九年级下学期 第一章 1.6 利用三角函数测高
一、单选题(共6题;共30分)
1.如图,河坝横断面迎水坡AB的坡比为1: ,坝高BC=4m,则AB的长度为(????? )
A.?2 m????????????????????????????????B.?4 m????????????????????????????????C.?4 m????????????????????????????????D.?6m
【答案】 C
【解析】【解答】解:∵迎水坡AB的坡度比为1:
∴, 即
解得,AC=4
根据勾股定理可得,AB==4
故答案为:C.
【分析】根据坡度的含义求出AC,继而由勾股定理计算得到AB即可。
2.如图,有一斜坡 的长 米,坡角 ,则斜坡 的铅垂高度 为(??? ).
A.???????????????????????????B.???????????????????????????C.???????????????????????????D.?
【答案】 C
【解析】【解答】解:结合题意,得:
∴
故答案为:C.
【分析】根据三角函数的定义,结合题意,即可得到答案.
3.如图,在莲花山滑雪场滑雪,需从山脚下乘缆车上山,缆车索道与水平线所成的角为31°,缆车速度为每分钟40米,从山脚下A到达山顶B缆车需要15分钟,则山的高度BC为( ??)
A.??????????????????????????B.??????????????????????????C.??????????????????????????D.?
【答案】 C
【解析】【解答】解:在直角三角形ABC中,
AB=40×15=600
∴sin∠BAC==
∴BC=600×sin31°
故答案为:C.
【分析】根据题意,由路程=时间×速度计算得到AB的长度,在直角三角形ABC中根据∠BAC的正弦求出BC的长度即可。
4.如图,数学活动小组利用测角仪和皮尺测量学校旗杆的高度,在点D处测得旗杆顶端A的仰角∠ADE为55°,测角仪CD的高度为1米,其底端C与旗杆底端B之间的距离为6米,设旗杆AB的高度为x米,则下列关系式正确的是(?? )
A.?tan55°= ??????????B.?tan55°= ??????????C.?sin55°= ??????????D.?cos55°=
【答案】 B
【解析】【解答】解:∵在Rt△ADE中,DE=6,AE=AB﹣BE=AB﹣CD=x﹣1,∠ADE=55°,
∴sin55°= ,cos55°= ,tan55°= ,
故答案为:B.
【分析】根据锐角三角形函数的定义“sin∠ADE=, cos∠ADE=, tan∠ADE=”并结合题意即可判断求解.
5.如图,垂直于水平面的5G信号塔AB建在垂直于水平面的悬崖边B点处,某测量员从山脚C点出发沿水平方向前行78米到D点(点A,B,C在同一直线上),再沿斜坡DE方向前行78米到E点(点A,B,C,D,E在同一平面内),在点E处测得5G信号塔顶端A的仰角为43°,悬崖BC的高为144.5米,斜坡DE的坡度(或坡比)i=1:2.4,则信号塔AB的高度约为(?? )
(参考数据:sin43°≈0.68,cos43°≈0.73,tan43°≈0.93)
A.?23米???????????????????????????????????B.?24米???????????????????????????????????C.?24.5米???????????????????????????????????D.?25米
【答案】 D
【解析】【解答】解:过点E作EF⊥DC交DC的延长线于点F,过点E作EM⊥AC于点M,
∵斜坡DE的坡度(或坡比)i=1:2.4,BE=CD=78米,
∴设EF=x,则DF=2.4x.
在Rt△DEF中,
∵EF2+DF2=DE2 , 即x2+(2.4x)2=782 ,
解得x=30,
∴EF=30米,DF=72米,
∴CF=DF+DC=72+78=150米.
∵EM⊥AC,AC⊥CD,EF⊥CD,
∴四边形EFCM是矩形,
∴EM=CF=150米,CM=EF=30米.
在Rt△AEM中,
∵∠AEM=43°,
∴AM=EM?tan43°≈150×0.93=139.5米,
∴AC=AM+CM=139.5+30=169.5米.
∴AB=AC﹣BC=169.5﹣144.5=25米.
故答案为:D.
【分析】由斜坡DE的坡度(或坡比)i=1:2.4可设EF=x,则DF=2.4x.由勾股定理可得EF2+DF2=DE2 , 即可求解EF、DF、CF,由AM=EM?tan43°可得AM、AC,即可求解AB.
6.如图,小明想要测量学校操场上旗杆 的高度,他作了如下操作:(1)在点C处放置测角仪,测得旗杆顶的仰角 ;(2)量得测角仪的高度 ;(3)量得测角仪到旗杆的水平距离 .利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为(?? )
A.??????????????????????????B.??????????????????????????C.??????????????????????????D.?
【答案】 A
【解析】【解答】延长CE交AB于F,如图,
根据题意得,四边形CDBF为矩形,
∴CF=DB=b,FB=CD=a,
在Rt△ACF中,∠ACF=α,CF=b,
tan∠ACF=
∴AF= ,
AB=AF+BF= ,
故答案为:A.
【分析】延长CE交AB于F,得四边形CDBF为矩形,故CF=DB=b,FB=CD=a,在直角三角形ACF中,利用CF的长和已知的角的度数,利用正切函数可求得AF的长,从而可求出旗杆AB的长.
二、填空题(共6题;共30分)
7.如图,一辆小车沿着坡度为 的斜坡从点A向上行驶了50米到点B处,则此时该小车离水平面的垂直高度为________.
【答案】 25
【解析】【解答】解:设此时该小车离水平面的垂直高度为x米,则水平前进了 x米.
根据勾股定理可得:x2+( x)2=502 .
解得x=25.
即此时该小车离水平面的垂直高度为25米.
故答案为:25.
【分析】设出垂直高度,表示出水平距离,利用勾股定理求解即可.
8.如图,航拍无人机从A处测得一幢建筑物顶部C的仰角是30°,测得底部B的俯角是60° ,此时无人机与该建筑物的水平距离AD是9米,那么该建筑物的高度BC为________米(结果保留根号).
【答案】
【解析】【解答】解:由题意,得∠CAD=30°,∠BAD=60°,
则在Rt△ADC中, 米,
在Rt△ADB中, 米,
∴ 米.
故答案为: .
【分析】由题意可得∠CAD=30°,∠BAD=60°,然后分别解Rt△ADC 和Rt△ADB,求出CD和BD的长,进一步即可求得结果.
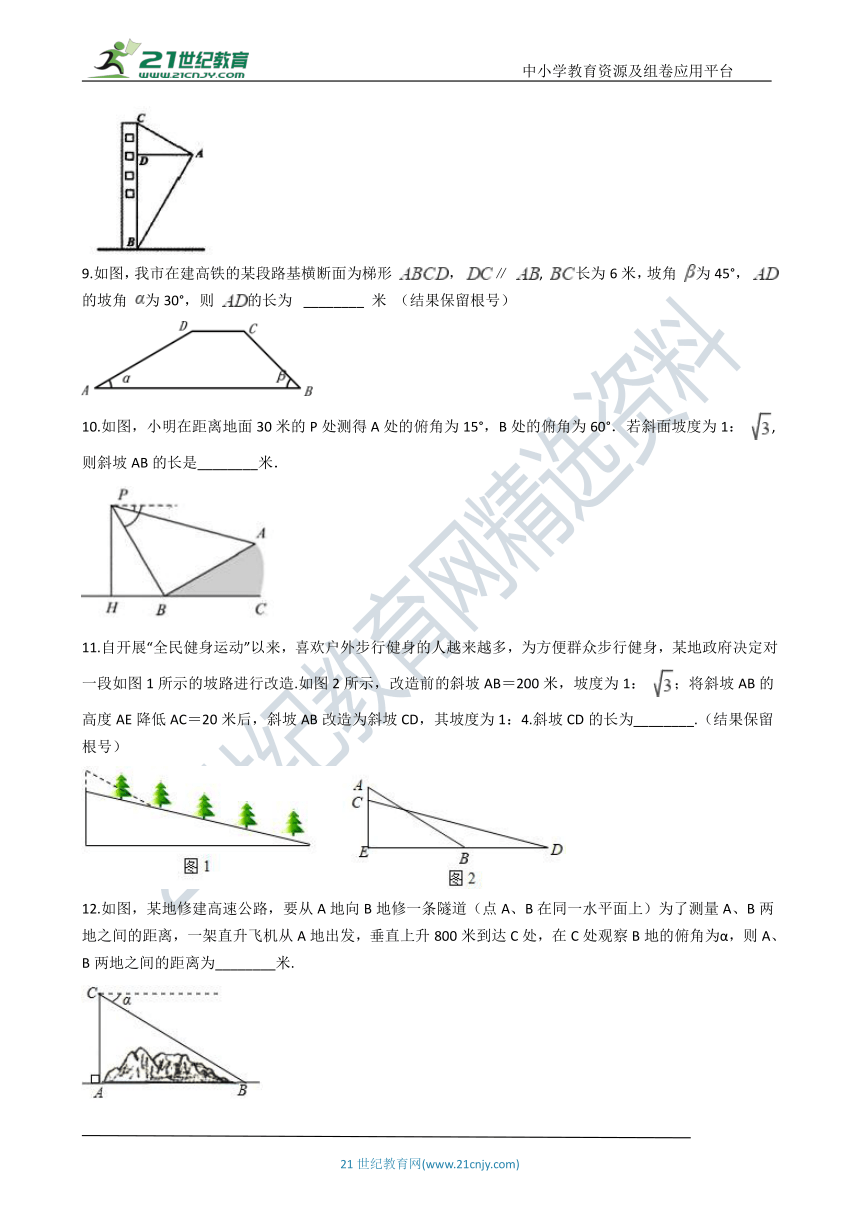
9.如图,我市在建高铁的某段路基横断面为梯形 , ∥ , 长为6米,坡角 为45°, 的坡角 为30°,则 的长为? ________ 米 (结果保留根号)
【答案】
【解析】【解答】解:过C作CE⊥AB于E,DF⊥AB于F,可得矩形CEFD和Rt△CEB与Rt△DFA,
∵BC=6,
∴CE= ,
∴DF=CE= ,
∴ ,
故答案为: .
【分析】过C作CE⊥AB于E,DF⊥AB于F,分别在Rt△CEB与Rt△DFA中使用三角函数即可求解.
10.如图,小明在距离地面30米的P处测得A处的俯角为15°,B处的俯角为60°.若斜面坡度为1: ,则斜坡AB的长是________米.
【答案】
【解析】【解答】解:如图所示:过点A作AF⊥BC于点F,
∵斜面坡度为1: ,
∴tan∠ABF= ,
∴∠ABF=30°,
∵在距离地面30米的P处测得A处的俯角为15°,B处的俯角为60°,
∴∠HPB=30°,∠APB=45°,
∴∠HBP=60°,
∴∠PBA=90°,∠BAP=45°,
∴PB=AB,
∵PH=30m,sin60°= ,
解得:PB= ,
故AB= m,
故答案为: .
【分析】首先根据题意得出∠ABF=30°,进而得出∠PBA=90°,∠BAP=45°,再利用锐角三角函数关系求出即可.
11.自开展“全民健身运动”以来,喜欢户外步行健身的人越来越多,为方便群众步行健身,某地政府决定对一段如图1所示的坡路进行改造.如图2所示,改造前的斜坡AB=200米,坡度为1: ;将斜坡AB的高度AE降低AC=20米后,斜坡AB改造为斜坡CD,其坡度为1:4.斜坡CD的长为________.(结果保留根号)
【答案】 米
【解析】【解答】解:∵∠AEB=90°,AB=200,坡度为1: ,
∴tan∠ABE= ,
∴∠ABE=30°,
∴AE= AB=100,
∵AC=20,
∴CE=80,
∵∠CED=90°,斜坡CD的坡度为1:4,
∴ ,
即 ,
解得,ED=320,
∴CD= = 米.
故答案为:米.
【分析】由AB坡度为1: ,可得tan∠ABE= ,利用特殊角三角函数值可得∠ABE=30°,从而可得AE= AB=100米,即得CE=AE-AC=80,由于斜坡CD的坡度为1:4,即得, 可求出ED=320,利用勾股定理求出CD的长即可.
12.如图,某地修建高速公路,要从A地向B地修一条隧道(点A、B在同一水平面上)为了测量A、B两地之间的距离,一架直升飞机从A地出发,垂直上升800米到达C处,在C处观察B地的俯角为α,则A、B两地之间的距离为________米.
【答案】
【解析】【解答】解:在Rt△ABC中,∵∠CAB=90°,∠B=α,AC=800米,
∴tanα= ,
∴AB= = (米).
故答案为: .
【分析】在Rt△ABC中,由tanα= 即可求出AB的长.
三、解答题(共4题;共40分)
13.如图,在一次数学课外实践活动中,要求测教学楼的高度AB、小刚在D处用高1.5m的测角仪CD , 测得教学楼顶端A的仰角为30°,然后向教学楼前进40m到达E , 又测得教学楼顶端A的仰角为60°.求这幢教学楼的高度AB . (结果带根号)
【答案】 解:在Rt△AFG中,tan∠AFG= ,
∴FG= = = .
在Rt△ACG中,tan∠ACG= ,
∴CG= = AG.
又CG?FG=40,
即 AG? =40,
∴AG=20 ,
∴AB=20 +1.5.
答:这幢教学楼的高度AB为(20 +1.5)米.
【解析】【分析】(1)在Rt△AFG中,由tan∠AFG=?, 可得 FG=?在Rt△ACG中,由tan∠ACG=?CG=AG,由CG?FG=40,建立方程求出AG的长,利用AB=AG+BG即可求出结论.
14.如图,在一次空中搜寻中,水平飞行的飞机在点A处测得前方海面的点F处有疑似飞机残骸的物体(该物体视为静止),此时的俯角为30°.为了便于观察,飞机继续向前飞行了800m到达B点,此时测得点F的俯角为45°.请你计算当飞机飞临F点的正上方点C时(点A,B,C在同一直线上),竖直高度CF约为多少米?(结果保留整数.参考数据: ≈1.7)
【答案】 解:∵∠BCF=90°,∠FBC=45°,
∴BC=CF,
∵∠CAF=30°,
∴tan 30°= = = = ,
解得:CF= ≈1046(m).
答:竖直高度CF约为1046米.
【解析】【分析】易得BC=CF,那么利用30°的正切值即可求得CF长.
15.东北师大附中为检测师生体温,在校门安装了某型号测温门,如图为该测温门截面示意图,已知测温门顶部A距地面高 ,为了解自己的有效测温区间,身高 的小明做了如下实验:当他在地面N处时, 测温门开始显示额头温度, 此时测得A的仰角 ;在地面M处时, 测温门停止显示额头温度, 此时测得A的仰角 求小明在地面的有效测温区间 的长度.(额头到地面的距离以身高计算,结果精确到 米)(参考数据: , , , , )
【答案】 解:延长BC交AD于点E,
,小明身高为 ,
故 ,
∴ ,
∵ , ,
∴ , ,
∴ , ,
即 , ,
∴ , ,
∴ , ,
∴ ,
易得四边形BCMN是矩形,
∴ ,
故 长度为 .
【解析】【分析】延长BC交AD于点E , 根据 , 求得EC和EB的长度,即可求解.
16.如图,点E与树AB的根部点A、建筑物CD的底部点C在一条直线上,AC=10m.小明站在点E处观测树顶B的仰角为30°,他从点E出发沿EC方向前进6m到点G时,观测树顶B的仰角为45°,此时恰好看不到建筑物CD的顶部D(H、B、D三点在一条直线上).已知小明的眼睛离地面1.6m,求建筑物CD的高度(结果精确到0.1m).(参考数据: ≈1.41, ≈1.73.)
【答案】 解:如图,延长FH,交CD于点M,交AB于点N,
∵ ∠BHN=45°,BA⊥MH,
则BN=NH,
设BN=NH=x,
∵ HF=6,∠BFN=30°,且tan∠BFN= = ,
∴tan30°= ,
解得x≈8.22,
根据题意可知:
DM=MH=MN+NH,
∵ MN=AC=10,
则DM=10+8.22=18.22,
∴ CD=DM+MC=DM+EF=18.22+1.6=19.82≈19.8(m).
答:建筑物CD的高度约为19.8m.
【解析】【分析】延长FH,交CD于点M,交AB于点N,求CD,只需求出DM即可,即只要求出HN就可以,在Rt△BNF中,设BN=NH=x,则根据tan∠BFN= 就可以求出x的值,再根据等腰直角三角形的性质和线段的和可求得CD的长.
一、单选题(共6题;共30分)
1.如图,河坝横断面迎水坡AB的坡比为1: ,坝高BC=4m,则AB的长度为(????? )
A.?2 m????????????????????????????????B.?4 m????????????????????????????????C.?4 m????????????????????????????????D.?6m
【答案】 C
【解析】【解答】解:∵迎水坡AB的坡度比为1:
∴, 即
解得,AC=4
根据勾股定理可得,AB==4
故答案为:C.
【分析】根据坡度的含义求出AC,继而由勾股定理计算得到AB即可。
2.如图,有一斜坡 的长 米,坡角 ,则斜坡 的铅垂高度 为(??? ).
A.???????????????????????????B.???????????????????????????C.???????????????????????????D.?
【答案】 C
【解析】【解答】解:结合题意,得:
∴
故答案为:C.
【分析】根据三角函数的定义,结合题意,即可得到答案.
3.如图,在莲花山滑雪场滑雪,需从山脚下乘缆车上山,缆车索道与水平线所成的角为31°,缆车速度为每分钟40米,从山脚下A到达山顶B缆车需要15分钟,则山的高度BC为( ??)
A.??????????????????????????B.??????????????????????????C.??????????????????????????D.?
【答案】 C
【解析】【解答】解:在直角三角形ABC中,
AB=40×15=600
∴sin∠BAC==
∴BC=600×sin31°
故答案为:C.
【分析】根据题意,由路程=时间×速度计算得到AB的长度,在直角三角形ABC中根据∠BAC的正弦求出BC的长度即可。
4.如图,数学活动小组利用测角仪和皮尺测量学校旗杆的高度,在点D处测得旗杆顶端A的仰角∠ADE为55°,测角仪CD的高度为1米,其底端C与旗杆底端B之间的距离为6米,设旗杆AB的高度为x米,则下列关系式正确的是(?? )
A.?tan55°= ??????????B.?tan55°= ??????????C.?sin55°= ??????????D.?cos55°=
【答案】 B
【解析】【解答】解:∵在Rt△ADE中,DE=6,AE=AB﹣BE=AB﹣CD=x﹣1,∠ADE=55°,
∴sin55°= ,cos55°= ,tan55°= ,
故答案为:B.
【分析】根据锐角三角形函数的定义“sin∠ADE=, cos∠ADE=, tan∠ADE=”并结合题意即可判断求解.
5.如图,垂直于水平面的5G信号塔AB建在垂直于水平面的悬崖边B点处,某测量员从山脚C点出发沿水平方向前行78米到D点(点A,B,C在同一直线上),再沿斜坡DE方向前行78米到E点(点A,B,C,D,E在同一平面内),在点E处测得5G信号塔顶端A的仰角为43°,悬崖BC的高为144.5米,斜坡DE的坡度(或坡比)i=1:2.4,则信号塔AB的高度约为(?? )
(参考数据:sin43°≈0.68,cos43°≈0.73,tan43°≈0.93)
A.?23米???????????????????????????????????B.?24米???????????????????????????????????C.?24.5米???????????????????????????????????D.?25米
【答案】 D
【解析】【解答】解:过点E作EF⊥DC交DC的延长线于点F,过点E作EM⊥AC于点M,
∵斜坡DE的坡度(或坡比)i=1:2.4,BE=CD=78米,
∴设EF=x,则DF=2.4x.
在Rt△DEF中,
∵EF2+DF2=DE2 , 即x2+(2.4x)2=782 ,
解得x=30,
∴EF=30米,DF=72米,
∴CF=DF+DC=72+78=150米.
∵EM⊥AC,AC⊥CD,EF⊥CD,
∴四边形EFCM是矩形,
∴EM=CF=150米,CM=EF=30米.
在Rt△AEM中,
∵∠AEM=43°,
∴AM=EM?tan43°≈150×0.93=139.5米,
∴AC=AM+CM=139.5+30=169.5米.
∴AB=AC﹣BC=169.5﹣144.5=25米.
故答案为:D.
【分析】由斜坡DE的坡度(或坡比)i=1:2.4可设EF=x,则DF=2.4x.由勾股定理可得EF2+DF2=DE2 , 即可求解EF、DF、CF,由AM=EM?tan43°可得AM、AC,即可求解AB.
6.如图,小明想要测量学校操场上旗杆 的高度,他作了如下操作:(1)在点C处放置测角仪,测得旗杆顶的仰角 ;(2)量得测角仪的高度 ;(3)量得测角仪到旗杆的水平距离 .利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为(?? )
A.??????????????????????????B.??????????????????????????C.??????????????????????????D.?
【答案】 A
【解析】【解答】延长CE交AB于F,如图,
根据题意得,四边形CDBF为矩形,
∴CF=DB=b,FB=CD=a,
在Rt△ACF中,∠ACF=α,CF=b,
tan∠ACF=
∴AF= ,
AB=AF+BF= ,
故答案为:A.
【分析】延长CE交AB于F,得四边形CDBF为矩形,故CF=DB=b,FB=CD=a,在直角三角形ACF中,利用CF的长和已知的角的度数,利用正切函数可求得AF的长,从而可求出旗杆AB的长.
二、填空题(共6题;共30分)
7.如图,一辆小车沿着坡度为 的斜坡从点A向上行驶了50米到点B处,则此时该小车离水平面的垂直高度为________.
【答案】 25
【解析】【解答】解:设此时该小车离水平面的垂直高度为x米,则水平前进了 x米.
根据勾股定理可得:x2+( x)2=502 .
解得x=25.
即此时该小车离水平面的垂直高度为25米.
故答案为:25.
【分析】设出垂直高度,表示出水平距离,利用勾股定理求解即可.
8.如图,航拍无人机从A处测得一幢建筑物顶部C的仰角是30°,测得底部B的俯角是60° ,此时无人机与该建筑物的水平距离AD是9米,那么该建筑物的高度BC为________米(结果保留根号).
【答案】
【解析】【解答】解:由题意,得∠CAD=30°,∠BAD=60°,
则在Rt△ADC中, 米,
在Rt△ADB中, 米,
∴ 米.
故答案为: .
【分析】由题意可得∠CAD=30°,∠BAD=60°,然后分别解Rt△ADC 和Rt△ADB,求出CD和BD的长,进一步即可求得结果.
9.如图,我市在建高铁的某段路基横断面为梯形 , ∥ , 长为6米,坡角 为45°, 的坡角 为30°,则 的长为? ________ 米 (结果保留根号)
【答案】
【解析】【解答】解:过C作CE⊥AB于E,DF⊥AB于F,可得矩形CEFD和Rt△CEB与Rt△DFA,
∵BC=6,
∴CE= ,
∴DF=CE= ,
∴ ,
故答案为: .
【分析】过C作CE⊥AB于E,DF⊥AB于F,分别在Rt△CEB与Rt△DFA中使用三角函数即可求解.
10.如图,小明在距离地面30米的P处测得A处的俯角为15°,B处的俯角为60°.若斜面坡度为1: ,则斜坡AB的长是________米.
【答案】
【解析】【解答】解:如图所示:过点A作AF⊥BC于点F,
∵斜面坡度为1: ,
∴tan∠ABF= ,
∴∠ABF=30°,
∵在距离地面30米的P处测得A处的俯角为15°,B处的俯角为60°,
∴∠HPB=30°,∠APB=45°,
∴∠HBP=60°,
∴∠PBA=90°,∠BAP=45°,
∴PB=AB,
∵PH=30m,sin60°= ,
解得:PB= ,
故AB= m,
故答案为: .
【分析】首先根据题意得出∠ABF=30°,进而得出∠PBA=90°,∠BAP=45°,再利用锐角三角函数关系求出即可.
11.自开展“全民健身运动”以来,喜欢户外步行健身的人越来越多,为方便群众步行健身,某地政府决定对一段如图1所示的坡路进行改造.如图2所示,改造前的斜坡AB=200米,坡度为1: ;将斜坡AB的高度AE降低AC=20米后,斜坡AB改造为斜坡CD,其坡度为1:4.斜坡CD的长为________.(结果保留根号)
【答案】 米
【解析】【解答】解:∵∠AEB=90°,AB=200,坡度为1: ,
∴tan∠ABE= ,
∴∠ABE=30°,
∴AE= AB=100,
∵AC=20,
∴CE=80,
∵∠CED=90°,斜坡CD的坡度为1:4,
∴ ,
即 ,
解得,ED=320,
∴CD= = 米.
故答案为:米.
【分析】由AB坡度为1: ,可得tan∠ABE= ,利用特殊角三角函数值可得∠ABE=30°,从而可得AE= AB=100米,即得CE=AE-AC=80,由于斜坡CD的坡度为1:4,即得, 可求出ED=320,利用勾股定理求出CD的长即可.
12.如图,某地修建高速公路,要从A地向B地修一条隧道(点A、B在同一水平面上)为了测量A、B两地之间的距离,一架直升飞机从A地出发,垂直上升800米到达C处,在C处观察B地的俯角为α,则A、B两地之间的距离为________米.
【答案】
【解析】【解答】解:在Rt△ABC中,∵∠CAB=90°,∠B=α,AC=800米,
∴tanα= ,
∴AB= = (米).
故答案为: .
【分析】在Rt△ABC中,由tanα= 即可求出AB的长.
三、解答题(共4题;共40分)
13.如图,在一次数学课外实践活动中,要求测教学楼的高度AB、小刚在D处用高1.5m的测角仪CD , 测得教学楼顶端A的仰角为30°,然后向教学楼前进40m到达E , 又测得教学楼顶端A的仰角为60°.求这幢教学楼的高度AB . (结果带根号)
【答案】 解:在Rt△AFG中,tan∠AFG= ,
∴FG= = = .
在Rt△ACG中,tan∠ACG= ,
∴CG= = AG.
又CG?FG=40,
即 AG? =40,
∴AG=20 ,
∴AB=20 +1.5.
答:这幢教学楼的高度AB为(20 +1.5)米.
【解析】【分析】(1)在Rt△AFG中,由tan∠AFG=?, 可得 FG=?在Rt△ACG中,由tan∠ACG=?CG=AG,由CG?FG=40,建立方程求出AG的长,利用AB=AG+BG即可求出结论.
14.如图,在一次空中搜寻中,水平飞行的飞机在点A处测得前方海面的点F处有疑似飞机残骸的物体(该物体视为静止),此时的俯角为30°.为了便于观察,飞机继续向前飞行了800m到达B点,此时测得点F的俯角为45°.请你计算当飞机飞临F点的正上方点C时(点A,B,C在同一直线上),竖直高度CF约为多少米?(结果保留整数.参考数据: ≈1.7)
【答案】 解:∵∠BCF=90°,∠FBC=45°,
∴BC=CF,
∵∠CAF=30°,
∴tan 30°= = = = ,
解得:CF= ≈1046(m).
答:竖直高度CF约为1046米.
【解析】【分析】易得BC=CF,那么利用30°的正切值即可求得CF长.
15.东北师大附中为检测师生体温,在校门安装了某型号测温门,如图为该测温门截面示意图,已知测温门顶部A距地面高 ,为了解自己的有效测温区间,身高 的小明做了如下实验:当他在地面N处时, 测温门开始显示额头温度, 此时测得A的仰角 ;在地面M处时, 测温门停止显示额头温度, 此时测得A的仰角 求小明在地面的有效测温区间 的长度.(额头到地面的距离以身高计算,结果精确到 米)(参考数据: , , , , )
【答案】 解:延长BC交AD于点E,
,小明身高为 ,
故 ,
∴ ,
∵ , ,
∴ , ,
∴ , ,
即 , ,
∴ , ,
∴ , ,
∴ ,
易得四边形BCMN是矩形,
∴ ,
故 长度为 .
【解析】【分析】延长BC交AD于点E , 根据 , 求得EC和EB的长度,即可求解.
16.如图,点E与树AB的根部点A、建筑物CD的底部点C在一条直线上,AC=10m.小明站在点E处观测树顶B的仰角为30°,他从点E出发沿EC方向前进6m到点G时,观测树顶B的仰角为45°,此时恰好看不到建筑物CD的顶部D(H、B、D三点在一条直线上).已知小明的眼睛离地面1.6m,求建筑物CD的高度(结果精确到0.1m).(参考数据: ≈1.41, ≈1.73.)
【答案】 解:如图,延长FH,交CD于点M,交AB于点N,
∵ ∠BHN=45°,BA⊥MH,
则BN=NH,
设BN=NH=x,
∵ HF=6,∠BFN=30°,且tan∠BFN= = ,
∴tan30°= ,
解得x≈8.22,
根据题意可知:
DM=MH=MN+NH,
∵ MN=AC=10,
则DM=10+8.22=18.22,
∴ CD=DM+MC=DM+EF=18.22+1.6=19.82≈19.8(m).
答:建筑物CD的高度约为19.8m.
【解析】【分析】延长FH,交CD于点M,交AB于点N,求CD,只需求出DM即可,即只要求出HN就可以,在Rt△BNF中,设BN=NH=x,则根据tan∠BFN= 就可以求出x的值,再根据等腰直角三角形的性质和线段的和可求得CD的长.
