4.3公式法-北师大版八年级数学下册课件(共23张PPT)
文档属性
| 名称 | 4.3公式法-北师大版八年级数学下册课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 325.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 00:00:00 | ||
图片预览








文档简介
八年级下册数学北师大版
第四章 因式分解
4.2 公式法
知识回顾
知识探究
练习提升
知识小结
回顾整式乘法中平方差公式和完全平方公式:
平方差公式:(a+b)(a-b)=a?-b?
完全平方公式:(a+b)?=a?+b?+2ab
(a-b)?= a?+b?-2ab
知识回顾
知识探究
练习提升
知识小结
用平方差公式进行因式分解:
平方差公式:(a+b)(a-b)=a?-b?
a?-b?=(a+b)(a-b)
反之
注意
a、b既可以是单项式也可以是多项式
知识回顾
知识探究
练习提升
知识小结
观察下列多项式,尝试将它们写成两个因式的乘积。
X?-25
9x?-y?
16-a?
X?-5?
(X+5)(x-5)
(3x)?-y?
(3X+y)(3x-y)
4?-a?
(4+a)(4-a)
共同特征:都是两个数的平方差形式!
知识回顾
知识探究
练习提升
知识小结
1、把下列各式因式分解:
25-16x?
9a?-? b?
a?b?-m?
-16x4+81y4
(5+4x)(5-4x)
(3a-?b)(3a+?b)
(ab+m)(ab-m)
(9y?+4x?)(9y?-4x?)
知识回顾
知识探究
练习提升
知识小结
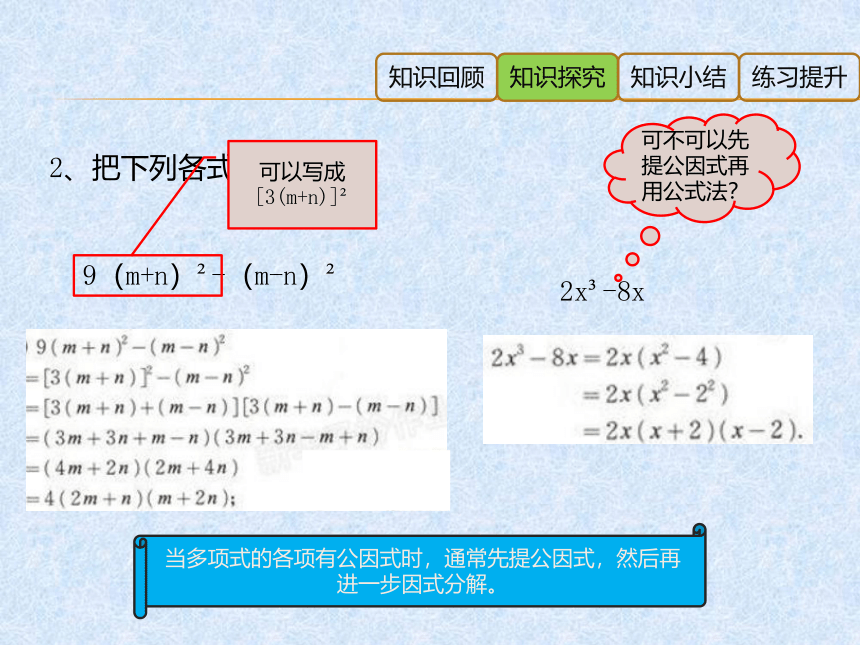
2、把下列各式因式分解:
9(m+n)?-(m-n)?
可以写成
[3(m+n)]?
2x?-8x
可不可以先提公因式再用公式法?
当多项式的各项有公因式时,通常先提公因式,然后再进一步因式分解。
知识回顾
知识探究
练习提升
知识小结
(m-a)?-(n+b)?
x?-(a+b-c)?
(m-a+n+b)(m-a-n-b)
(x+a+b-c)(x-a-b+c)
知识回顾
知识探究
练习提升
知识小结
1、 一个多项式如果能化成两个整式平方差的形式,就可以用平方差公式分解。即:
a?-b?=(a+b)(a-b)
2、 因式分解时,若有公因式,应先提公因式,再用公式法因式分解,且分解要彻底。
总结
知识回顾
知识探究
练习提升
知识小结
1、将多项式m?-4进行因式分解,结论正确的是( )
A.(m+2)(m-2) B. ( m+4)(m-4)
C.(m-2)? D.(m+2)?
A
知识回顾
知识探究
练习提升
知识小结
2、下列多项式中,能用平方差公式分解因式的是( )
A.a?+b? B.- a?-b? C. -a?+b? D. a?-ab
C
知识回顾
知识探究
练习提升
知识小结
C
3、把多项式2x?-8分解因式,结果正确的是( )
A.2(x?-8) B.2(x-2)?
C.2(x+2)(x-2) D.2x(x-4/x)
知识回顾
知识探究
练习提升
知识小结
4、下列因式分解中,结果正确的是( )
A.2m?-2m=2m(m?-1)
B.x?-4x=x(x+2)(x-2)
C.4x?-16y?=(2x+4y)(2x-4y)
D.8a?b-2b?=2b(2a+b)(2a-b)
D
知识回顾
知识探究
练习提升
知识小结
5、如图,已知R=6.75,r=3.25,则图中阴影部分的面积为( )
A.3.5π B.12.25π C.27π D.35π
D
知识回顾
知识探究
练习提升
知识小结
6、已知长方形的面积是9a?-16(a>4/3),若一边长为3a+4,则另一边长为________.
3a-4
7、已知|x-y+2|+√(x+y-2)=0,则x?-y?的值为_______.
-4
知识回顾
知识探究
练习提升
知识小结
用完全平方公式进行因式分解:
(a+b)?=a?+b?+2ab (a-b)?= a?+b?-2ab
a?+b?+2ab= (a+b)? a?+b?-2ab = ( a-b)?
反之
整式乘法
因式分解
知识回顾
知识探究
练习提升
知识小结
例如,将下列式子进行因式分解:
x?-4x+4 9x?+6xy+y?
=x?-2 · x · 2+2?
=(x-2)?
=(3x)?+2 · 3x · y+y?
=(3x+y)?
知识回顾
知识探究
练习提升
知识小结
根据整式乘法和因式分解的关系,我们可以利用乘法公式把某些多项式因式分解,这种因式分解的方法叫做公式法。
公式法
知识回顾
知识探究
练习提升
知识小结
因式分解的一般步骤:
1、如果多项式的各项含有公因式,那么应先提取公因式;
2、如果多项式的各项不含有公因式,那么可以尝试运用公式法因式分解(即平方差公式和完全平方公式);
3、如果上述方法都不能进行因式分解,那么可以先整理多项式,然后分解;
4、因式分解必须分解到每一个因式都不能再分解为止。
遵循“一提、二套、三检查”的原则
知识回顾
知识探究
练习提升
知识小结
1、用公式法因式分解下列式子:
(1)(2x+3y)?-1
(2)-3x?+6xy-3y?
(3)-(x+2)?+16(x-1)?
(4)(a+b)?-2(a+b)+1
第一项系数为负,一般要提取“-”,使括号内的第一项为正。
(a+b)看作一个整体
(2x+3y+1)
-3(x-y)?
3(5x-2)(x-2)
(a+b-1)?
知识回顾
知识探究
练习提升
知识小结
2、综合运用多种方式因式分解:
(1)4x?y-36xy?
(2)x4-2x?+1
(3)x?y+2x?y?+xy?
(4)9x?(a-b)+y?(b-a)
综合分解因式根据“一提、二套、三检查”的原则解题即可
4xy(x+3y)(x-3y)
(x+1)?(x-1)?
xy(x+y)?
(a-b)(3x+y)(3x-y)
知识回顾
知识探究
练习提升
知识小结
3、利用因式分解化简求值
a4-4a?b+4a?b?,其中,a=8,b=-2.
原式=9216
知识回顾
知识探究
练习提升
知识小结
4、因式分解在整除中的应用
原式=4(n-2)(n+3)
n是正数,则4(n-2)(n+3)能被4整除
若n为整数,试说明(2n+1)?-25能被4整除。
知识回顾
知识探究
练习提升
知识小结
公式法分解因式:
平方差公式和完全平方公式
分解因式的步骤:
一提、二套、三检查
第四章 因式分解
4.2 公式法
知识回顾
知识探究
练习提升
知识小结
回顾整式乘法中平方差公式和完全平方公式:
平方差公式:(a+b)(a-b)=a?-b?
完全平方公式:(a+b)?=a?+b?+2ab
(a-b)?= a?+b?-2ab
知识回顾
知识探究
练习提升
知识小结
用平方差公式进行因式分解:
平方差公式:(a+b)(a-b)=a?-b?
a?-b?=(a+b)(a-b)
反之
注意
a、b既可以是单项式也可以是多项式
知识回顾
知识探究
练习提升
知识小结
观察下列多项式,尝试将它们写成两个因式的乘积。
X?-25
9x?-y?
16-a?
X?-5?
(X+5)(x-5)
(3x)?-y?
(3X+y)(3x-y)
4?-a?
(4+a)(4-a)
共同特征:都是两个数的平方差形式!
知识回顾
知识探究
练习提升
知识小结
1、把下列各式因式分解:
25-16x?
9a?-? b?
a?b?-m?
-16x4+81y4
(5+4x)(5-4x)
(3a-?b)(3a+?b)
(ab+m)(ab-m)
(9y?+4x?)(9y?-4x?)
知识回顾
知识探究
练习提升
知识小结
2、把下列各式因式分解:
9(m+n)?-(m-n)?
可以写成
[3(m+n)]?
2x?-8x
可不可以先提公因式再用公式法?
当多项式的各项有公因式时,通常先提公因式,然后再进一步因式分解。
知识回顾
知识探究
练习提升
知识小结
(m-a)?-(n+b)?
x?-(a+b-c)?
(m-a+n+b)(m-a-n-b)
(x+a+b-c)(x-a-b+c)
知识回顾
知识探究
练习提升
知识小结
1、 一个多项式如果能化成两个整式平方差的形式,就可以用平方差公式分解。即:
a?-b?=(a+b)(a-b)
2、 因式分解时,若有公因式,应先提公因式,再用公式法因式分解,且分解要彻底。
总结
知识回顾
知识探究
练习提升
知识小结
1、将多项式m?-4进行因式分解,结论正确的是( )
A.(m+2)(m-2) B. ( m+4)(m-4)
C.(m-2)? D.(m+2)?
A
知识回顾
知识探究
练习提升
知识小结
2、下列多项式中,能用平方差公式分解因式的是( )
A.a?+b? B.- a?-b? C. -a?+b? D. a?-ab
C
知识回顾
知识探究
练习提升
知识小结
C
3、把多项式2x?-8分解因式,结果正确的是( )
A.2(x?-8) B.2(x-2)?
C.2(x+2)(x-2) D.2x(x-4/x)
知识回顾
知识探究
练习提升
知识小结
4、下列因式分解中,结果正确的是( )
A.2m?-2m=2m(m?-1)
B.x?-4x=x(x+2)(x-2)
C.4x?-16y?=(2x+4y)(2x-4y)
D.8a?b-2b?=2b(2a+b)(2a-b)
D
知识回顾
知识探究
练习提升
知识小结
5、如图,已知R=6.75,r=3.25,则图中阴影部分的面积为( )
A.3.5π B.12.25π C.27π D.35π
D
知识回顾
知识探究
练习提升
知识小结
6、已知长方形的面积是9a?-16(a>4/3),若一边长为3a+4,则另一边长为________.
3a-4
7、已知|x-y+2|+√(x+y-2)=0,则x?-y?的值为_______.
-4
知识回顾
知识探究
练习提升
知识小结
用完全平方公式进行因式分解:
(a+b)?=a?+b?+2ab (a-b)?= a?+b?-2ab
a?+b?+2ab= (a+b)? a?+b?-2ab = ( a-b)?
反之
整式乘法
因式分解
知识回顾
知识探究
练习提升
知识小结
例如,将下列式子进行因式分解:
x?-4x+4 9x?+6xy+y?
=x?-2 · x · 2+2?
=(x-2)?
=(3x)?+2 · 3x · y+y?
=(3x+y)?
知识回顾
知识探究
练习提升
知识小结
根据整式乘法和因式分解的关系,我们可以利用乘法公式把某些多项式因式分解,这种因式分解的方法叫做公式法。
公式法
知识回顾
知识探究
练习提升
知识小结
因式分解的一般步骤:
1、如果多项式的各项含有公因式,那么应先提取公因式;
2、如果多项式的各项不含有公因式,那么可以尝试运用公式法因式分解(即平方差公式和完全平方公式);
3、如果上述方法都不能进行因式分解,那么可以先整理多项式,然后分解;
4、因式分解必须分解到每一个因式都不能再分解为止。
遵循“一提、二套、三检查”的原则
知识回顾
知识探究
练习提升
知识小结
1、用公式法因式分解下列式子:
(1)(2x+3y)?-1
(2)-3x?+6xy-3y?
(3)-(x+2)?+16(x-1)?
(4)(a+b)?-2(a+b)+1
第一项系数为负,一般要提取“-”,使括号内的第一项为正。
(a+b)看作一个整体
(2x+3y+1)
-3(x-y)?
3(5x-2)(x-2)
(a+b-1)?
知识回顾
知识探究
练习提升
知识小结
2、综合运用多种方式因式分解:
(1)4x?y-36xy?
(2)x4-2x?+1
(3)x?y+2x?y?+xy?
(4)9x?(a-b)+y?(b-a)
综合分解因式根据“一提、二套、三检查”的原则解题即可
4xy(x+3y)(x-3y)
(x+1)?(x-1)?
xy(x+y)?
(a-b)(3x+y)(3x-y)
知识回顾
知识探究
练习提升
知识小结
3、利用因式分解化简求值
a4-4a?b+4a?b?,其中,a=8,b=-2.
原式=9216
知识回顾
知识探究
练习提升
知识小结
4、因式分解在整除中的应用
原式=4(n-2)(n+3)
n是正数,则4(n-2)(n+3)能被4整除
若n为整数,试说明(2n+1)?-25能被4整除。
知识回顾
知识探究
练习提升
知识小结
公式法分解因式:
平方差公式和完全平方公式
分解因式的步骤:
一提、二套、三检查
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
