北师大版八年级数学 下册课件:4.3用乘法公式分解因式(2)——完全平方公式(共26张PPT)
文档属性
| 名称 | 北师大版八年级数学 下册课件:4.3用乘法公式分解因式(2)——完全平方公式(共26张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 1017.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 00:00:00 | ||
图片预览







文档简介
1.优先考虑提取公因式法,分解因式;
2. 把握平方差公式结构特征;
3.分解因式后各因式要合并化简,且分解要彻底。
现在我们把完全平方公式反过来,可得:
两个数的平方和,加上 这两个数的积的两倍,等于这两数和 的平方.
完全平方公式:
(或减去)
(或者差)
两个数的平方和,加上(或减去)这两个数的积的两倍,等于这两数和(或者差)的平方.
形如 的多项式称为完全平方式.
1.判别下列各式是不是完全平方式.
不是
是
是
不是
你能总结出完全平方式的特点吗?
是
完全平方式的特点:
1. 有三项组成.
2.有两项分别是某两个数(或式)的平方,
3. 另一项是上述两数(或式)的乘积的2倍,
且这两项同号.
符号可正可负.
a2 + 2ab + b2 = ( a + b )2
a2-2ab+b2 =(a-b)2
16x2+40x+25= ( )2+2( )( )+( )2 =( + )2
=( )2- 2( )( )+( )2 =( - )2
4x
4x
4x
5
5
5
公式中的a、b可以表示数、字母、单项式甚至是多项式
n
n
n
对照公式填一填
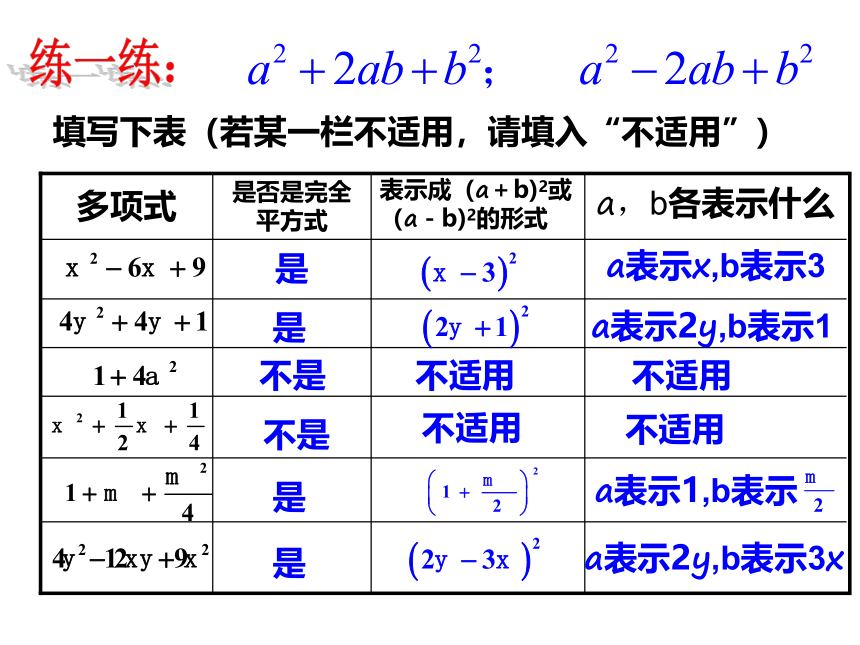
填写下表(若某一栏不适用,请填入“不适用”)
a表示x,b表示3
a,b各表示什么
表示成(a+b)2或(a-b)2的形式
是
是否是完全平方式
多项式
是
a表示2y,b表示1
不是
不适用
不适用
不适用
不适用
不是
是
a表示1,b表示
是
a表示2y,b表示3x
是否是完全平方式
a、b各表示什么
表示(a+b)2或(a-b)2
是
a表示2y,
b表示1
否
否
否
是
a表示2y,
b表示3x
是
a表示(a+b),
b表示1
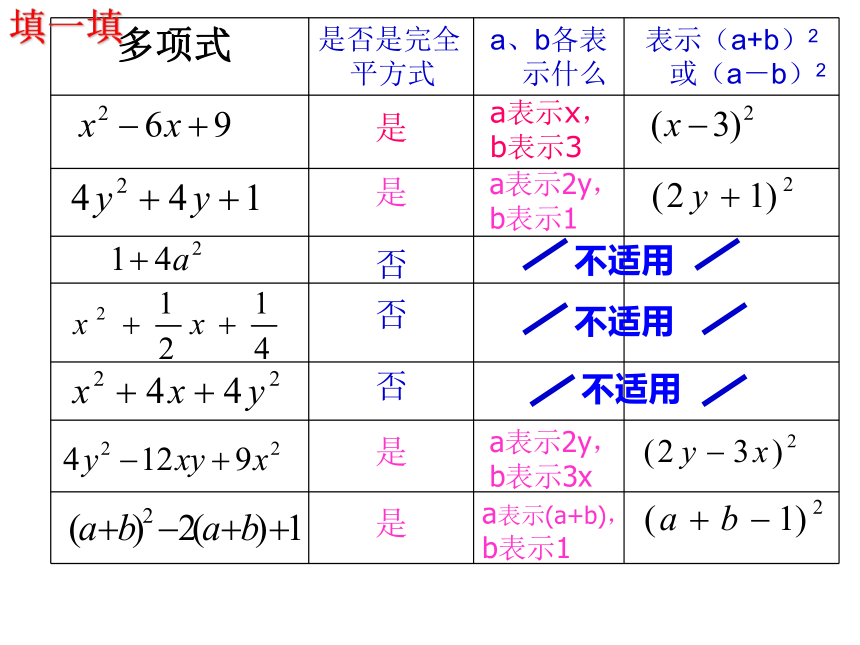
填一填
多项式
是
a表示x,
b表示3
不适用
不适用
不适用
是否是完
全平方式
a、b各表示什么
表示(a+b)2或(a-b)2
否
否
是
a表示 ,
b表示3n
填一填
多项式
是
a表示x,
b表示1/2
是
a表示1,
b表示
不适用
不适用
填空:
(1)a2+ +b2=(a+b)2
(2)a2-2ab+ =(a-b) 2
(3)m2+2m+ =( ) 2
(4)n2-2n+ =( ) 2
(5)x2-x+0.25=( ) 2
(6)4x2+4xy+( ) 2=( ) 2
2ab
b2
1
m+1
1
n-1
x-0.5
y
2x+y
在下列多项式中添加一项,并写成完全平方式的形式。
例1.把下列完全平方式分解因式:
找到完全平方式中的“头”和“尾”,确定中间项的符号。
解:原式 解:原式
完全平方式中的“头”和“尾”,可以是数字、字母,也可以是单项式或多项式。
完全平方式中的“头”和“尾”,可以是数字、字母,也可以是单项式或多项式。
练习 把下列各式分解因式:
例2 把下列各式分解因式:
1.若多项式中有公因式,应先提取公因式,然后再进一步分解因式。
2.当平方项系数为负时,应先将负号提出
3.观察多项式结构特征,灵活运用公式分解因式;
4.分解因式要彻底。
练习
分解因式:
提高训练:
1.分解因式:
(1)用简便方法计算:
绝对挑战
2.按照完全平方公式填空:
绝对挑战
(3)将 再加上一项,使它成为
完全平方式,你有几种方法?
一天,小明在纸上写了一个算式为
x2 +6x+11,并对小刚说:“无论x取何值,这
个代数式的值都是正值,你不信试一试?”
1. 已知 ,
求 的值
绝对挑战
2.两个连续奇数的平方差能被8整除吗?为什么?
3. 已知 ,
求 的值
4.已知x2+4x+y2-2y+5=0,求 x-y 的值。
解:由x2+4x+y2-2y+5=(x2+4x+4)+(y2-2y+1)
=(x+2)2+(y-1)2=0得
x+2=0,y-1=0
∴x=-2,y=1
∴x-y=(-2)-1=
(1)形如________________形式的多项式可以用完全平方公式分解因式。
(3)因式分解要_________
(2)因式分解通常先考虑______________方法。再考虑——方法。
提取公因式法
彻底
平方差公式
完全平方公式
会选择合适的公式进行因式分解
1、有两项
1、有三项
2、两项可写成数或式的平
方形式,且符号相同
2、两项可写成数或式的
平方形式,且符号相
反
3、一项是两数乘积的两倍
从下面8张纸片中任意找出3张纸片组成一个多项式(不改变原有符号,可重复使用),使得它能用完全平方公式进行因式分解
2. 把握平方差公式结构特征;
3.分解因式后各因式要合并化简,且分解要彻底。
现在我们把完全平方公式反过来,可得:
两个数的平方和,加上 这两个数的积的两倍,等于这两数和 的平方.
完全平方公式:
(或减去)
(或者差)
两个数的平方和,加上(或减去)这两个数的积的两倍,等于这两数和(或者差)的平方.
形如 的多项式称为完全平方式.
1.判别下列各式是不是完全平方式.
不是
是
是
不是
你能总结出完全平方式的特点吗?
是
完全平方式的特点:
1. 有三项组成.
2.有两项分别是某两个数(或式)的平方,
3. 另一项是上述两数(或式)的乘积的2倍,
且这两项同号.
符号可正可负.
a2 + 2ab + b2 = ( a + b )2
a2-2ab+b2 =(a-b)2
16x2+40x+25= ( )2+2( )( )+( )2 =( + )2
=( )2- 2( )( )+( )2 =( - )2
4x
4x
4x
5
5
5
公式中的a、b可以表示数、字母、单项式甚至是多项式
n
n
n
对照公式填一填
填写下表(若某一栏不适用,请填入“不适用”)
a表示x,b表示3
a,b各表示什么
表示成(a+b)2或(a-b)2的形式
是
是否是完全平方式
多项式
是
a表示2y,b表示1
不是
不适用
不适用
不适用
不适用
不是
是
a表示1,b表示
是
a表示2y,b表示3x
是否是完全平方式
a、b各表示什么
表示(a+b)2或(a-b)2
是
a表示2y,
b表示1
否
否
否
是
a表示2y,
b表示3x
是
a表示(a+b),
b表示1
填一填
多项式
是
a表示x,
b表示3
不适用
不适用
不适用
是否是完
全平方式
a、b各表示什么
表示(a+b)2或(a-b)2
否
否
是
a表示 ,
b表示3n
填一填
多项式
是
a表示x,
b表示1/2
是
a表示1,
b表示
不适用
不适用
填空:
(1)a2+ +b2=(a+b)2
(2)a2-2ab+ =(a-b) 2
(3)m2+2m+ =( ) 2
(4)n2-2n+ =( ) 2
(5)x2-x+0.25=( ) 2
(6)4x2+4xy+( ) 2=( ) 2
2ab
b2
1
m+1
1
n-1
x-0.5
y
2x+y
在下列多项式中添加一项,并写成完全平方式的形式。
例1.把下列完全平方式分解因式:
找到完全平方式中的“头”和“尾”,确定中间项的符号。
解:原式 解:原式
完全平方式中的“头”和“尾”,可以是数字、字母,也可以是单项式或多项式。
完全平方式中的“头”和“尾”,可以是数字、字母,也可以是单项式或多项式。
练习 把下列各式分解因式:
例2 把下列各式分解因式:
1.若多项式中有公因式,应先提取公因式,然后再进一步分解因式。
2.当平方项系数为负时,应先将负号提出
3.观察多项式结构特征,灵活运用公式分解因式;
4.分解因式要彻底。
练习
分解因式:
提高训练:
1.分解因式:
(1)用简便方法计算:
绝对挑战
2.按照完全平方公式填空:
绝对挑战
(3)将 再加上一项,使它成为
完全平方式,你有几种方法?
一天,小明在纸上写了一个算式为
x2 +6x+11,并对小刚说:“无论x取何值,这
个代数式的值都是正值,你不信试一试?”
1. 已知 ,
求 的值
绝对挑战
2.两个连续奇数的平方差能被8整除吗?为什么?
3. 已知 ,
求 的值
4.已知x2+4x+y2-2y+5=0,求 x-y 的值。
解:由x2+4x+y2-2y+5=(x2+4x+4)+(y2-2y+1)
=(x+2)2+(y-1)2=0得
x+2=0,y-1=0
∴x=-2,y=1
∴x-y=(-2)-1=
(1)形如________________形式的多项式可以用完全平方公式分解因式。
(3)因式分解要_________
(2)因式分解通常先考虑______________方法。再考虑——方法。
提取公因式法
彻底
平方差公式
完全平方公式
会选择合适的公式进行因式分解
1、有两项
1、有三项
2、两项可写成数或式的平
方形式,且符号相同
2、两项可写成数或式的
平方形式,且符号相
反
3、一项是两数乘积的两倍
从下面8张纸片中任意找出3张纸片组成一个多项式(不改变原有符号,可重复使用),使得它能用完全平方公式进行因式分解
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
