北师大版八年级数学下册5.4分式方程第1课时 认识分式方程课件(共35张PPT)
文档属性
| 名称 | 北师大版八年级数学下册5.4分式方程第1课时 认识分式方程课件(共35张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 19:29:39 | ||
图片预览











文档简介
5.4分式方程
第1课时 认识分式方程
学习目标(1分钟)
理解分式方程的概念,并会根据实际问题的数量关系列分式方程。
自学指导1:(6分钟)
自学课本P125做一做之前的内容,思考所提出的几个问题:
甲、乙两地相距 1400 km,乘高铁列车从甲地到乙地比乘特快列车少用 9 h,已知高铁列车的平均行驶速度是特快列车的 2.8 倍.
(1)你能找出这一问题中的所有等量关系吗?
(2)如果设特快列车的平均行驶速度为 x km/h,那么 x 满足怎样的方程?
(3)如果设小明乘高铁列车从甲地到乙地需 y h,那么 y 满足怎样的方程?
1、列车的速度×行驶时间=1400
2、乘高铁列车行驶时间=乘特快列车的行驶时间﹣9
3、高铁列车的平均速度=特快列车平均速度× 2.8
(2)如果设特快列车的平均行驶速度为 x km/h,那么 x 满足怎样的方程?
(3)如果设小明乘高铁列车从甲地到乙地需 y h,那么 y 满足怎样的方程?
(1)等量关系:
议一议
为了帮助遭受自然灾害的地区重建家园,某学校号召同学们自愿捐款,已知七年级捐款总额为4800元,八年级捐款总额5000元,八年级捐款人数比七年级多20人,而且两个年级人均捐款额正好相等,如果设七年级捐款的人数为x人,请列出关于x的方程。
捐款总额
捐款人 数
人均捐款额
第一次
第二次
X+20
4800元
5000元
x
议一议
比较左右两边的方程, 有什么不同?
谁能试说一下什么是分式方程?
自学指导2:(5分钟)
自学课本P125议一议的内容,思考所提出的问题:
%
上面所得到的方程有什么共同特点?
分母中含有未知数的方程叫做分式方程。
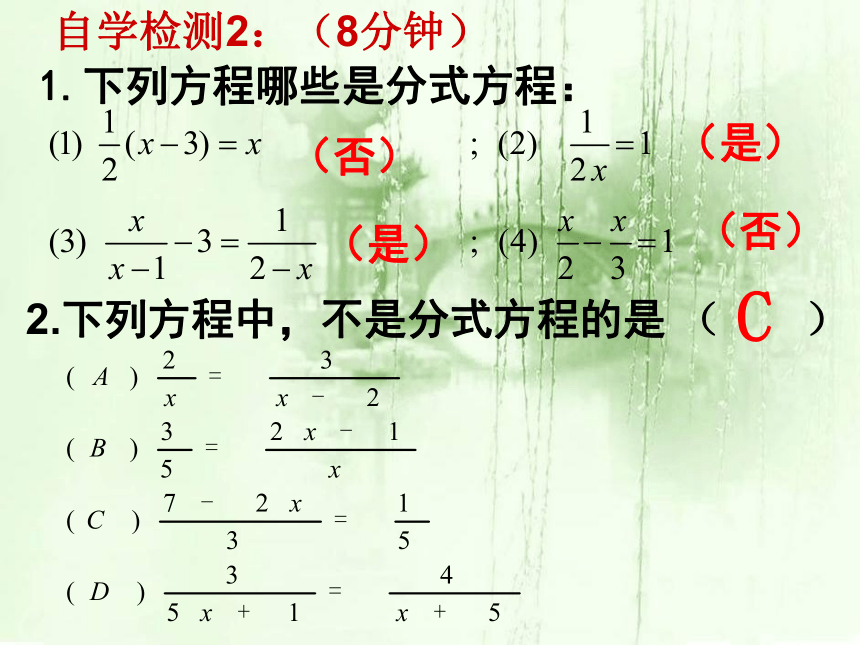
1.下列方程哪些是分式方程:
自学检测2:(8分钟)
(否)
(否)
(是)
(是)
2.下列方程中,不是分式方程的是 ( )
C
随堂练习T1
答案校对:
(1-12%)=950
%
%
某商场有管理人员40人,销售人员80人,为了提高服务水平和销售量,商场决定从管理人员中抽调一部分人充实销售部分,使管理人员与销售人员的人数比为1:4,那么应抽调的管理人员数x,满足怎样的方程?
方程为:
练一练
等量关系:
实际参加活动的人数=原定人数×2
原计划平均分摊的费用=实际平均分摊的费用+4元。
补充:王军同学准备在课外活动时间组织部分同学参加电脑网络培训,按原定的人数估计共需费用300元。后因人数增加到原定人数的2倍,费用享受了优惠,一共只需要480元,参加活动的每个同学平均分摊的费用比原计划少4元,原定的人数是多少?如果设原定是x人,那么 x 满足怎样的分式方程?
从甲地到乙地有两条路可以走:一条全长600 km普通公路,另一条是全长 480km 的高速公路,某客车在高速公路上行驶的平均速度比普通公路上快45km/h,由高速公路从甲地到乙地的所需的时间是由普通公路从甲地到乙地所需时间的一半,求该客车由高速公路从甲地到乙地所需要的时间?
点拨:T3
高速公路
普通公路
路程
速度
时间
路程
速度
时间
480km
x
600 km
2x
(1)、你能发现这个问题中的等量关系吗?
(2)、你能根据等量关系列出分式方程吗?
走高速公路的速度= 走普通公路的速度- 45
点拨:T3
学 习 新 知
问题思考
【问题1】 写出 与 的最简公分母.
【问题2】 解一元一次方程 .
例1 解方程
所以,x=3是原方程的根.
解:方程两边都乘x(x-2),得
x=3(x-2).
解这个方程,得 x=3.
检验:将x=3代入原方程,得
左边=1,右边=1,左边=右边.
例2 解方程
经检验,x=4是原方程的根.
解:方程两边都乘2x,得
960-600=90x.
解这个方程,得 x=4.
想一想:
解分式方程一般需要经过哪几个步骤?
3.解分式方程可能产生使最简公分母为零的增根,因此检验是解分式方程必要的步骤.
1.把分式方程化为整式方程的方法是去掉分式方程中的分母.如何去掉分式方程中的分母是解分式方程的“关键”步骤.
2.用分式方程中各式的最简公分母分别乘方程的两边,从而约去分母.但要注意用最简公分母乘方程两边的每一项,切勿漏项.
[知识拓展]
检测反馈
1.关于x的方程 的解是( )
A.x=4 B.x=3 C.x=2 D.x=1
B
2.分式方程 的解为 ( )
A.x=1 B.x=2 C.x=3 D.x=4
C
3.方程 的根是 .?
解析:方程两边同乘最简公分母x(x+1),得3x=2x+2,解这个方程,得x=2,经检验,x=2是原方程的根.所以方程 的根是x=2.故填x=2.
x=2
回忆一下
答题
1.列一元一次方程解应用题的一般步骤分哪几步?
审题
找等量关系
设未知数
列方程
解方程
2.解分式方程的一般步骤:
4、写:
写出结论
1、化:
把分式方程化为整式方程
2、解:
解整式方程
3、检验:
检验是否为增根
某单位将沿街的一部分房屋出租.每间房屋的租金第二年比第一年多500元,所有房屋出租的租金第一年为9.6万元,第二年为10.2万元.
(1)你能找出这一情境中的等量关系吗?
(2)根据这一情境你能提出哪些问题?
某单位将沿街的一部分房屋出租.每间房屋的租金第二年比第一年多500元,所有房屋出租的租金第一年为9.6万元,第二年为10.2万元.
1.你能找出这一情境中的等量关系吗?
第二年每间房屋租金=第一年每间房屋租金+500元
第一年出租的房屋间数=第二年出租的房屋间数
等量关系有下面一些:
出租的房屋间数=所有出租房屋的租金÷
每间房屋的租金
2.根据这一情境你能提出哪些问题?
答:(1)求出租的房屋总间数;
(2)分别求两年每间房屋的租金.
(1)解:设出租的房屋总间数为x间,则第一年每间房屋的租金为 元,第二年每间房屋的租金为 元,根据题意得:
解得 x=12,经检验x=12是所列方程的根,
所以出租的房屋总间数为12间。
做一做:某单位将沿街的一部分房屋出租,每间房屋的租金第二年比第一年多500元,所有房屋的租金第一年为9.6万元,第二年为10.2万元。
(1)求出租的房屋总间数;
例1:某单位将沿街的一部分房屋出租,每间房屋的租金第二年比第一年多500元,所有房屋的租金第一年为9.6万元,第二年为10.2万元。
(2)分别求两年每间房屋的租金
解:设第一年每间房屋的租金为x元,则第二年每间房屋的租金为(x+500)元,根据题意,得
解这个方程得: x =8000
经检验 x =8000是所列方程的根
所以,8000+500=8500(元)
答:第一年每间房屋的租金为8000元,第二年每间房屋的租金为8500元。
例1:某单位将沿街的一部分房屋出租,每间房屋的租金第二年比第一年多500元,所有房屋的租金第一年为9.6万元,第二年为10.2万元。
(2)分别求两年每间房屋的租金
解:设共有x套房间 ,根据题意,得
解这个方程得: x =12
经检验 x =12是所列方程的根
所以,102000÷12=8500(元),96000÷12=8000(元)
答:第一年每间房屋的租金为8000元,第二年每间房屋的租金为8500元。
例3.某市从今年1月1日起调整居民用水价格,每立方米水费涨价1/3.小丽家去年12月份的水费15元,而今年7月份的水费是30元.已知小丽家今年7月份的用水量比去年12月份的用水量多5立方米,求该市今年居民用水的价格.
主要等量关系是:
小丽家今年7月份的用水量-小丽家去年12月份的用水量=5 m3
今年用水价格=去年用水价格×(1+1/3)
解:设去年用水的价格为x元/m3,则今年的水价为 ,
根据题意,得
解这个方程,得:x=1.5
经检验, x=1.5 是所列方程的根.
答:该市今年居民用水的价格为2元/m3.
列分式方程解应用题的一般步骤:
审——己知未知量
设——(所求问题中)未知数
列——(数学模型)方程
解——(所列数学模型)方程
验——是否合乎题意
答——答题
1、小明和同学去书店买书,他们先用15元买了一种科普书,又用15元买了一种文学书。科普书的价格比文学书高出一半,他们所买的科普书比文学书少1本。这种科普书和这种文学书的价格各是多少?
解:设文学书的价格是本x元/本,则科普书1.5x元/本.
依题意得:
解得 x = 5
答:文学书的价格是每本5元,科普书每本7.5元
经检验 x = 5是所列方程的根。
∴1.5x=1.5×5=7.5(元)
1、小明和同学去书店买书,他们先用15元买了一种科普书,又用15元买了一种文学书。科普书的价格比文学书高出一半,他们所买的科普书比文学书少1本。这种科普书和这种文学书的价格各是多少?
课后作业
2.甲、乙两人练习骑自行车,已知甲每小时比乙多走6千米,甲骑90千米所用的时间和乙骑60千米所用时间相等,求甲、乙每小时各骑多少千米?
解得 x=18
经检验 x=18 是所列方程的根。
x - 6=12(千米)
答:甲每小时骑18千米,乙每小时骑12千米。
解:设甲每小时骑x千米,则乙每小时骑(x-6)千米。依题意得:
第1课时 认识分式方程
学习目标(1分钟)
理解分式方程的概念,并会根据实际问题的数量关系列分式方程。
自学指导1:(6分钟)
自学课本P125做一做之前的内容,思考所提出的几个问题:
甲、乙两地相距 1400 km,乘高铁列车从甲地到乙地比乘特快列车少用 9 h,已知高铁列车的平均行驶速度是特快列车的 2.8 倍.
(1)你能找出这一问题中的所有等量关系吗?
(2)如果设特快列车的平均行驶速度为 x km/h,那么 x 满足怎样的方程?
(3)如果设小明乘高铁列车从甲地到乙地需 y h,那么 y 满足怎样的方程?
1、列车的速度×行驶时间=1400
2、乘高铁列车行驶时间=乘特快列车的行驶时间﹣9
3、高铁列车的平均速度=特快列车平均速度× 2.8
(2)如果设特快列车的平均行驶速度为 x km/h,那么 x 满足怎样的方程?
(3)如果设小明乘高铁列车从甲地到乙地需 y h,那么 y 满足怎样的方程?
(1)等量关系:
议一议
为了帮助遭受自然灾害的地区重建家园,某学校号召同学们自愿捐款,已知七年级捐款总额为4800元,八年级捐款总额5000元,八年级捐款人数比七年级多20人,而且两个年级人均捐款额正好相等,如果设七年级捐款的人数为x人,请列出关于x的方程。
捐款总额
捐款人 数
人均捐款额
第一次
第二次
X+20
4800元
5000元
x
议一议
比较左右两边的方程, 有什么不同?
谁能试说一下什么是分式方程?
自学指导2:(5分钟)
自学课本P125议一议的内容,思考所提出的问题:
%
上面所得到的方程有什么共同特点?
分母中含有未知数的方程叫做分式方程。
1.下列方程哪些是分式方程:
自学检测2:(8分钟)
(否)
(否)
(是)
(是)
2.下列方程中,不是分式方程的是 ( )
C
随堂练习T1
答案校对:
(1-12%)=950
%
%
某商场有管理人员40人,销售人员80人,为了提高服务水平和销售量,商场决定从管理人员中抽调一部分人充实销售部分,使管理人员与销售人员的人数比为1:4,那么应抽调的管理人员数x,满足怎样的方程?
方程为:
练一练
等量关系:
实际参加活动的人数=原定人数×2
原计划平均分摊的费用=实际平均分摊的费用+4元。
补充:王军同学准备在课外活动时间组织部分同学参加电脑网络培训,按原定的人数估计共需费用300元。后因人数增加到原定人数的2倍,费用享受了优惠,一共只需要480元,参加活动的每个同学平均分摊的费用比原计划少4元,原定的人数是多少?如果设原定是x人,那么 x 满足怎样的分式方程?
从甲地到乙地有两条路可以走:一条全长600 km普通公路,另一条是全长 480km 的高速公路,某客车在高速公路上行驶的平均速度比普通公路上快45km/h,由高速公路从甲地到乙地的所需的时间是由普通公路从甲地到乙地所需时间的一半,求该客车由高速公路从甲地到乙地所需要的时间?
点拨:T3
高速公路
普通公路
路程
速度
时间
路程
速度
时间
480km
x
600 km
2x
(1)、你能发现这个问题中的等量关系吗?
(2)、你能根据等量关系列出分式方程吗?
走高速公路的速度= 走普通公路的速度- 45
点拨:T3
学 习 新 知
问题思考
【问题1】 写出 与 的最简公分母.
【问题2】 解一元一次方程 .
例1 解方程
所以,x=3是原方程的根.
解:方程两边都乘x(x-2),得
x=3(x-2).
解这个方程,得 x=3.
检验:将x=3代入原方程,得
左边=1,右边=1,左边=右边.
例2 解方程
经检验,x=4是原方程的根.
解:方程两边都乘2x,得
960-600=90x.
解这个方程,得 x=4.
想一想:
解分式方程一般需要经过哪几个步骤?
3.解分式方程可能产生使最简公分母为零的增根,因此检验是解分式方程必要的步骤.
1.把分式方程化为整式方程的方法是去掉分式方程中的分母.如何去掉分式方程中的分母是解分式方程的“关键”步骤.
2.用分式方程中各式的最简公分母分别乘方程的两边,从而约去分母.但要注意用最简公分母乘方程两边的每一项,切勿漏项.
[知识拓展]
检测反馈
1.关于x的方程 的解是( )
A.x=4 B.x=3 C.x=2 D.x=1
B
2.分式方程 的解为 ( )
A.x=1 B.x=2 C.x=3 D.x=4
C
3.方程 的根是 .?
解析:方程两边同乘最简公分母x(x+1),得3x=2x+2,解这个方程,得x=2,经检验,x=2是原方程的根.所以方程 的根是x=2.故填x=2.
x=2
回忆一下
答题
1.列一元一次方程解应用题的一般步骤分哪几步?
审题
找等量关系
设未知数
列方程
解方程
2.解分式方程的一般步骤:
4、写:
写出结论
1、化:
把分式方程化为整式方程
2、解:
解整式方程
3、检验:
检验是否为增根
某单位将沿街的一部分房屋出租.每间房屋的租金第二年比第一年多500元,所有房屋出租的租金第一年为9.6万元,第二年为10.2万元.
(1)你能找出这一情境中的等量关系吗?
(2)根据这一情境你能提出哪些问题?
某单位将沿街的一部分房屋出租.每间房屋的租金第二年比第一年多500元,所有房屋出租的租金第一年为9.6万元,第二年为10.2万元.
1.你能找出这一情境中的等量关系吗?
第二年每间房屋租金=第一年每间房屋租金+500元
第一年出租的房屋间数=第二年出租的房屋间数
等量关系有下面一些:
出租的房屋间数=所有出租房屋的租金÷
每间房屋的租金
2.根据这一情境你能提出哪些问题?
答:(1)求出租的房屋总间数;
(2)分别求两年每间房屋的租金.
(1)解:设出租的房屋总间数为x间,则第一年每间房屋的租金为 元,第二年每间房屋的租金为 元,根据题意得:
解得 x=12,经检验x=12是所列方程的根,
所以出租的房屋总间数为12间。
做一做:某单位将沿街的一部分房屋出租,每间房屋的租金第二年比第一年多500元,所有房屋的租金第一年为9.6万元,第二年为10.2万元。
(1)求出租的房屋总间数;
例1:某单位将沿街的一部分房屋出租,每间房屋的租金第二年比第一年多500元,所有房屋的租金第一年为9.6万元,第二年为10.2万元。
(2)分别求两年每间房屋的租金
解:设第一年每间房屋的租金为x元,则第二年每间房屋的租金为(x+500)元,根据题意,得
解这个方程得: x =8000
经检验 x =8000是所列方程的根
所以,8000+500=8500(元)
答:第一年每间房屋的租金为8000元,第二年每间房屋的租金为8500元。
例1:某单位将沿街的一部分房屋出租,每间房屋的租金第二年比第一年多500元,所有房屋的租金第一年为9.6万元,第二年为10.2万元。
(2)分别求两年每间房屋的租金
解:设共有x套房间 ,根据题意,得
解这个方程得: x =12
经检验 x =12是所列方程的根
所以,102000÷12=8500(元),96000÷12=8000(元)
答:第一年每间房屋的租金为8000元,第二年每间房屋的租金为8500元。
例3.某市从今年1月1日起调整居民用水价格,每立方米水费涨价1/3.小丽家去年12月份的水费15元,而今年7月份的水费是30元.已知小丽家今年7月份的用水量比去年12月份的用水量多5立方米,求该市今年居民用水的价格.
主要等量关系是:
小丽家今年7月份的用水量-小丽家去年12月份的用水量=5 m3
今年用水价格=去年用水价格×(1+1/3)
解:设去年用水的价格为x元/m3,则今年的水价为 ,
根据题意,得
解这个方程,得:x=1.5
经检验, x=1.5 是所列方程的根.
答:该市今年居民用水的价格为2元/m3.
列分式方程解应用题的一般步骤:
审——己知未知量
设——(所求问题中)未知数
列——(数学模型)方程
解——(所列数学模型)方程
验——是否合乎题意
答——答题
1、小明和同学去书店买书,他们先用15元买了一种科普书,又用15元买了一种文学书。科普书的价格比文学书高出一半,他们所买的科普书比文学书少1本。这种科普书和这种文学书的价格各是多少?
解:设文学书的价格是本x元/本,则科普书1.5x元/本.
依题意得:
解得 x = 5
答:文学书的价格是每本5元,科普书每本7.5元
经检验 x = 5是所列方程的根。
∴1.5x=1.5×5=7.5(元)
1、小明和同学去书店买书,他们先用15元买了一种科普书,又用15元买了一种文学书。科普书的价格比文学书高出一半,他们所买的科普书比文学书少1本。这种科普书和这种文学书的价格各是多少?
课后作业
2.甲、乙两人练习骑自行车,已知甲每小时比乙多走6千米,甲骑90千米所用的时间和乙骑60千米所用时间相等,求甲、乙每小时各骑多少千米?
解得 x=18
经检验 x=18 是所列方程的根。
x - 6=12(千米)
答:甲每小时骑18千米,乙每小时骑12千米。
解:设甲每小时骑x千米,则乙每小时骑(x-6)千米。依题意得:
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
