北师大版八年级数学下册课件:3.2图形的旋转(1)(共35张PPT)
文档属性
| 名称 | 北师大版八年级数学下册课件:3.2图形的旋转(1)(共35张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 19:31:00 | ||
图片预览






文档简介
(共32张PPT)
第三章 图形的平移与旋转
沈阳南昌数学
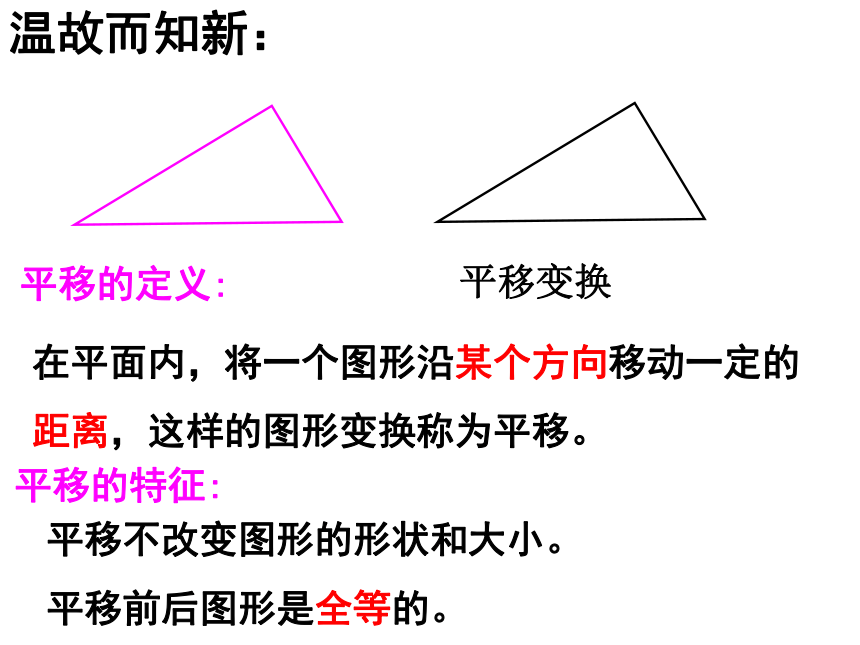
平移变换
平移的定义:
在平面内,将一个图形沿某个方向移动一定的距离,这样的图形变换称为平移。
平移不改变图形的形状和大小。
平移前后图形是全等的。
平移的特征:
温故而知新:
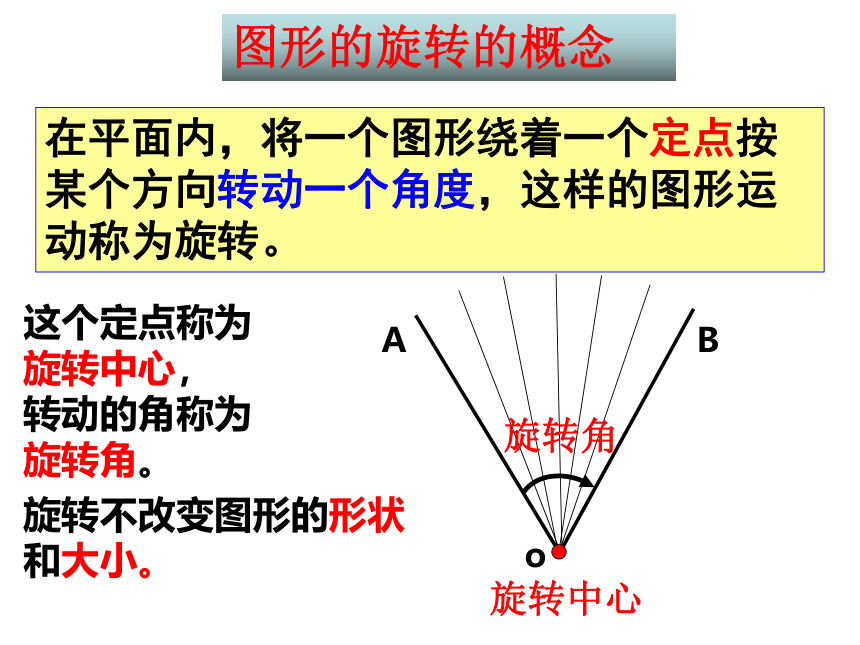
这个定点称为
旋转中心,
转动的角称为
旋转角。
旋转角
旋转中心
在平面内,将一个图形绕着一个定点按某个方向转动一个角度,这样的图形运动称为旋转。
A
o
B
图形的旋转的概念
旋转不改变图形的形状和大小。
B
O
A
45
0
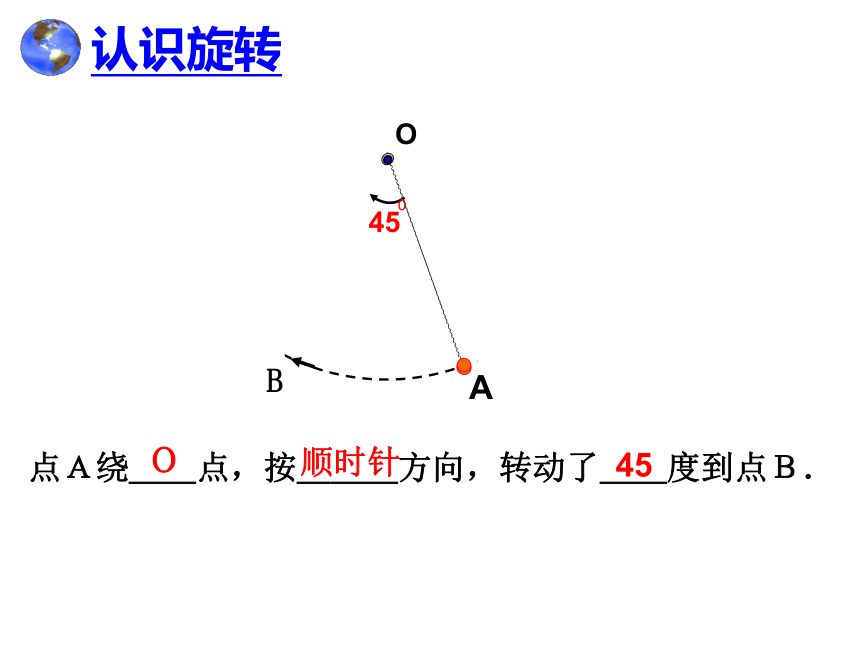
点A绕__点,按___方向,转动了__度到点B.
O
顺时针
45
认识旋转
B
A
认识旋转
B
A
C
C
O
100
0
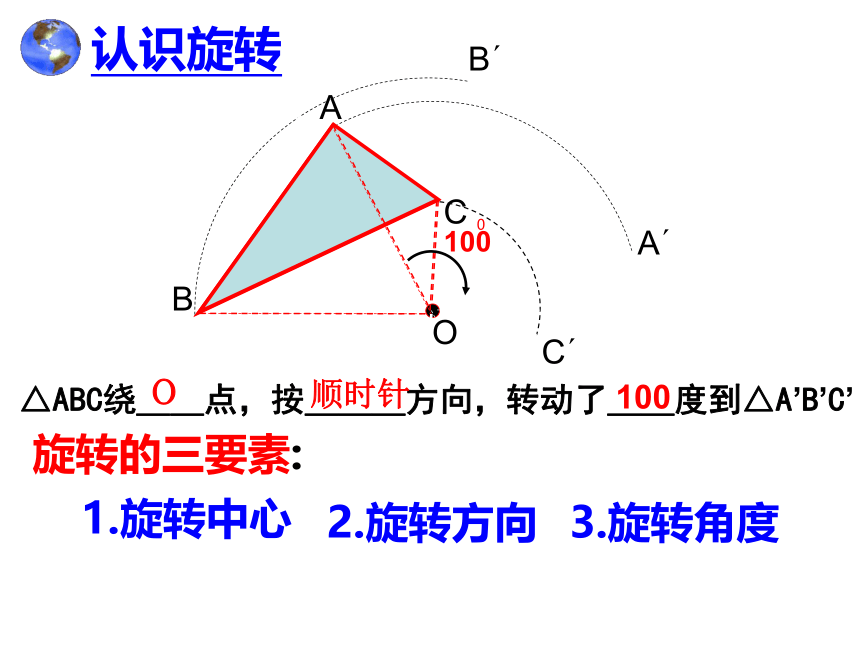
1.旋转中心
3.旋转角度
2.旋转方向
旋转的三要素:
△ABC绕__点,按___方向,转动了__度到△A’B’C’ .
O
顺时针
100
下列现象中属于旋转的有( )个
①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.
A.2 B.3 C.4 D.5
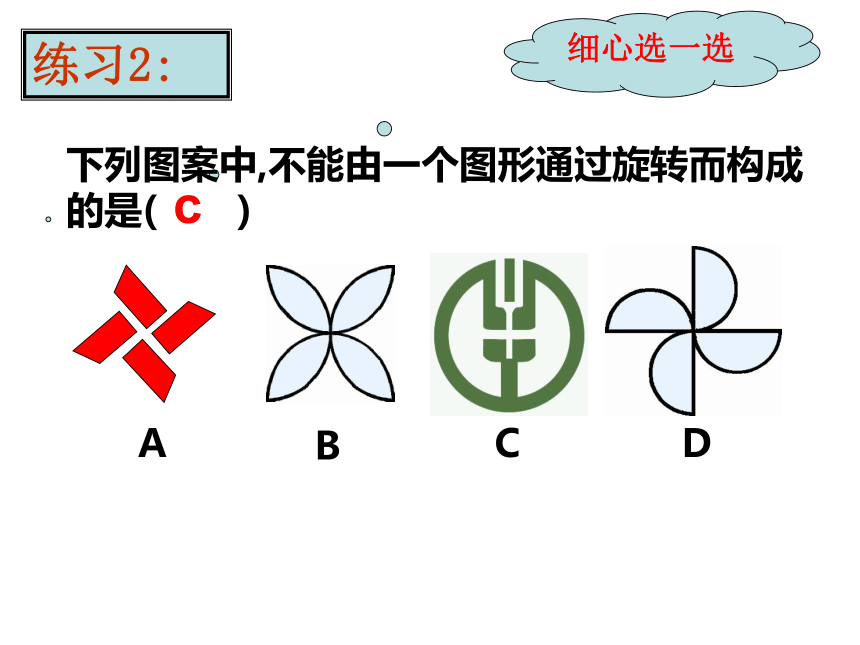
练习1:
c
细心选一选
下列图案中,不能由一个图形通过旋转而构成的是( )
A
C
D
B
c
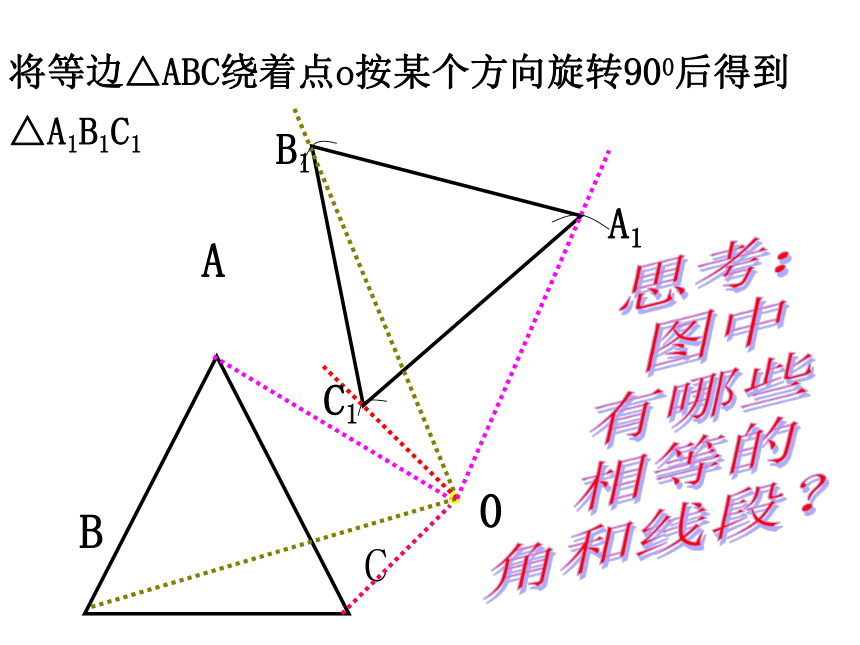
练习2:
将等边△ABC绕着点o按某个方向旋转900后得到△A1B1C1
A
B
C
.
0
C1
B1
A1
如图,如果把钟表的指针看做四边形AOBC,它绕O点旋转得到四边形DOEF. 在这个旋转过程中
议一议
旋转中心是O
点D和点E
AO=DO,BO=EO
∠AOD=∠BOE
∠AOD和∠BOE都是旋转角
(1)旋转中心是什么
(2)经过旋转点A、B分别移动到什么位置?
(3)旋转角是什么?
(5)∠AOD与∠BOE有什么大小关系?
(4)AO与DO的长有什么关系?BO与EO呢?
∠COF也是旋转角
(1)对应点到旋转中心的距离相等;
旋转的基本性质
一个图形和它经过旋转所得图形中,
(3)对应线段相等,对应角相等。
(2)任意一对对应点与旋转中心的连线所成的角都等于旋转角;
(旋转不改变图形的形状和大小,
旋转前后的图形全等)
45
B'
A'
O
B
A
45
如图,△ A′O B′是△AOB绕点O按顺时针方向旋转45°角度所得的。
A'
B'
B
O
A
这里定点 是旋转中心,旋转角是45°的角度
为 。
小试牛刀
点O
∠AOA′, ∠ BOB′
点B的对应点是点_____
线段OB的对应线段是线段______
∠A的对应角是______
线段AB的对应线段是线段______
B'
0B’
A ′ B ′
∠A'
如图,如果正方形CDEF旋转后能与正方形ABCD重合,那么图形所在的平面上可以作为旋转中心的点共有______个.
练习1
3
(2)旋转中心是哪一点?旋转了多少度?
练习2
如图,四边形ABCD是正方形,E是AD上任意一点,延长BA到F使得AF=AE,连接DF:
(3)BE与DF的数量关系、
位置关系如何 为什么
点 A,900
相等、垂直
(1)旋转△ADF可得到哪个三角形?
△ABE
图案欣赏
知识点归纳
1. 旋转的定义:“三要素”
旋转中心、旋转方向、旋转角.
2. 旋转的性质:“三特点”
对应点到旋转中心的距离相等;
对应点与旋转中心的连线所成的角都是旋转角;
对应线段相等,对应角相等。
3. 旋转图形的形成描述:“五说明”
基本图形、旋转中心、方向、次数、旋转角.
“这个图案可以看成是 绕点 按 时针方向旋转 次,分别旋转 前后的所有图形共同组成的。”
“三、三、五”
如图,正方形ABCD中,E是CD边上任意一点,将三角形ADE顺时针旋转,得到三角形ABF。
A
D
C
B
E
F
(4)连结EF,
(2)旋转了多少度?
(1)旋转中心是哪一点?
(3)点M是AD的中点,
M
M/
挑战自我
90°
等腰直角三角形
经上述旋转后,点M到
什么位置?
△AEF是什么三角形
如图,正方形ABCD中,E是CD边上任意一点,将三角形ADE顺时针旋转,得到三角形ABF。
A
D
C
B
E
F
M
M/
(5)若正方形ABCD的边长是2,
①则点M在旋转时经过的路径
长是多少?
②求四边形AFCE的面积。
4
练习:本图案可以看做是一个菱形通过几次旋转得到的?每次旋转了多少度?
也可以看做是二个相邻菱形通过几次旋转得到的?每次旋转了多少度?
还可以看做是几个菱形通过几次旋转得到的?每次旋转了多少度?
3个 1次 1800
2次 1200 , 2400
5次 600, 1200, 1800, 2400, 3000
3个 1次 600
做一做:
在图中,正方形ABCD与正方形EFGH边长相等,这个图案可以看作是哪个“基本图案”通过旋转得到的.
课堂回顾:这节课,主要学习了什么?
在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转
旋转的概念:
旋转的性质:
1、旋转不改变图形的大小和形状.旋转前、后
的图形全等.
2、任意一对对应点与旋转中心的连线所成的
角度都是旋转角,旋转角相等.
3、对应点到旋转中心的距离相等
拓展练习1
图案可以看作是一个菱形通过几次旋转得到的?
每次旋转了多少角度?
图案可以看作是一个菱形通过几次旋转得到的?
每次旋转了多少角度?
拓展练习1
答:旋转5次得到,旋转角度分别等于60°, 120°, 180°, 240°, 300°.
拓展练习2:
下图可看作是一个等腰三角形通过几次旋转得到的?每次旋转多少度?
答:旋转7次得到,旋转角度分别等于45°, 90°, 135°, 180°, 225°, 270 °,315°.
例1:钟表的分针匀速旋转一周需要60分.
(1)指出它的旋转中心;
(2)经过20分,分针旋转了多少度?
(2)分针匀速旋转一周需要60分,因此旋转
20分,分针旋转的角度为
解:(1)它的旋转中心是钟表的轴心;
第三章 图形的平移与旋转
沈阳南昌数学
平移变换
平移的定义:
在平面内,将一个图形沿某个方向移动一定的距离,这样的图形变换称为平移。
平移不改变图形的形状和大小。
平移前后图形是全等的。
平移的特征:
温故而知新:
这个定点称为
旋转中心,
转动的角称为
旋转角。
旋转角
旋转中心
在平面内,将一个图形绕着一个定点按某个方向转动一个角度,这样的图形运动称为旋转。
A
o
B
图形的旋转的概念
旋转不改变图形的形状和大小。
B
O
A
45
0
点A绕__点,按___方向,转动了__度到点B.
O
顺时针
45
认识旋转
B
A
认识旋转
B
A
C
C
O
100
0
1.旋转中心
3.旋转角度
2.旋转方向
旋转的三要素:
△ABC绕__点,按___方向,转动了__度到△A’B’C’ .
O
顺时针
100
下列现象中属于旋转的有( )个
①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.
A.2 B.3 C.4 D.5
练习1:
c
细心选一选
下列图案中,不能由一个图形通过旋转而构成的是( )
A
C
D
B
c
练习2:
将等边△ABC绕着点o按某个方向旋转900后得到△A1B1C1
A
B
C
.
0
C1
B1
A1
如图,如果把钟表的指针看做四边形AOBC,它绕O点旋转得到四边形DOEF. 在这个旋转过程中
议一议
旋转中心是O
点D和点E
AO=DO,BO=EO
∠AOD=∠BOE
∠AOD和∠BOE都是旋转角
(1)旋转中心是什么
(2)经过旋转点A、B分别移动到什么位置?
(3)旋转角是什么?
(5)∠AOD与∠BOE有什么大小关系?
(4)AO与DO的长有什么关系?BO与EO呢?
∠COF也是旋转角
(1)对应点到旋转中心的距离相等;
旋转的基本性质
一个图形和它经过旋转所得图形中,
(3)对应线段相等,对应角相等。
(2)任意一对对应点与旋转中心的连线所成的角都等于旋转角;
(旋转不改变图形的形状和大小,
旋转前后的图形全等)
45
B'
A'
O
B
A
45
如图,△ A′O B′是△AOB绕点O按顺时针方向旋转45°角度所得的。
A'
B'
B
O
A
这里定点 是旋转中心,旋转角是45°的角度
为 。
小试牛刀
点O
∠AOA′, ∠ BOB′
点B的对应点是点_____
线段OB的对应线段是线段______
∠A的对应角是______
线段AB的对应线段是线段______
B'
0B’
A ′ B ′
∠A'
如图,如果正方形CDEF旋转后能与正方形ABCD重合,那么图形所在的平面上可以作为旋转中心的点共有______个.
练习1
3
(2)旋转中心是哪一点?旋转了多少度?
练习2
如图,四边形ABCD是正方形,E是AD上任意一点,延长BA到F使得AF=AE,连接DF:
(3)BE与DF的数量关系、
位置关系如何 为什么
点 A,900
相等、垂直
(1)旋转△ADF可得到哪个三角形?
△ABE
图案欣赏
知识点归纳
1. 旋转的定义:“三要素”
旋转中心、旋转方向、旋转角.
2. 旋转的性质:“三特点”
对应点到旋转中心的距离相等;
对应点与旋转中心的连线所成的角都是旋转角;
对应线段相等,对应角相等。
3. 旋转图形的形成描述:“五说明”
基本图形、旋转中心、方向、次数、旋转角.
“这个图案可以看成是 绕点 按 时针方向旋转 次,分别旋转 前后的所有图形共同组成的。”
“三、三、五”
如图,正方形ABCD中,E是CD边上任意一点,将三角形ADE顺时针旋转,得到三角形ABF。
A
D
C
B
E
F
(4)连结EF,
(2)旋转了多少度?
(1)旋转中心是哪一点?
(3)点M是AD的中点,
M
M/
挑战自我
90°
等腰直角三角形
经上述旋转后,点M到
什么位置?
△AEF是什么三角形
如图,正方形ABCD中,E是CD边上任意一点,将三角形ADE顺时针旋转,得到三角形ABF。
A
D
C
B
E
F
M
M/
(5)若正方形ABCD的边长是2,
①则点M在旋转时经过的路径
长是多少?
②求四边形AFCE的面积。
4
练习:本图案可以看做是一个菱形通过几次旋转得到的?每次旋转了多少度?
也可以看做是二个相邻菱形通过几次旋转得到的?每次旋转了多少度?
还可以看做是几个菱形通过几次旋转得到的?每次旋转了多少度?
3个 1次 1800
2次 1200 , 2400
5次 600, 1200, 1800, 2400, 3000
3个 1次 600
做一做:
在图中,正方形ABCD与正方形EFGH边长相等,这个图案可以看作是哪个“基本图案”通过旋转得到的.
课堂回顾:这节课,主要学习了什么?
在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转
旋转的概念:
旋转的性质:
1、旋转不改变图形的大小和形状.旋转前、后
的图形全等.
2、任意一对对应点与旋转中心的连线所成的
角度都是旋转角,旋转角相等.
3、对应点到旋转中心的距离相等
拓展练习1
图案可以看作是一个菱形通过几次旋转得到的?
每次旋转了多少角度?
图案可以看作是一个菱形通过几次旋转得到的?
每次旋转了多少角度?
拓展练习1
答:旋转5次得到,旋转角度分别等于60°, 120°, 180°, 240°, 300°.
拓展练习2:
下图可看作是一个等腰三角形通过几次旋转得到的?每次旋转多少度?
答:旋转7次得到,旋转角度分别等于45°, 90°, 135°, 180°, 225°, 270 °,315°.
例1:钟表的分针匀速旋转一周需要60分.
(1)指出它的旋转中心;
(2)经过20分,分针旋转了多少度?
(2)分针匀速旋转一周需要60分,因此旋转
20分,分针旋转的角度为
解:(1)它的旋转中心是钟表的轴心;
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
