北师大版八年级数学下第六章6.4多边形及其内角和教学课件 (共38张PPT)
文档属性
| 名称 | 北师大版八年级数学下第六章6.4多边形及其内角和教学课件 (共38张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 19:50:41 | ||
图片预览




文档简介
§6.4多边形的内角和
1、在平面内, _____________________ 叫做多边形。
2、在多边形中连接 _________________ 的线段叫做多边形的对角线。
3、三角形的内角和是_____度.
4、你能够利用三角形的内角和求四边形的内角和吗?试试看?
思路:多边形问题转化为三角形问题来解决.
由一些线段首尾顺次相接组成的图形
多边形不相邻的两个顶点的线段
1800
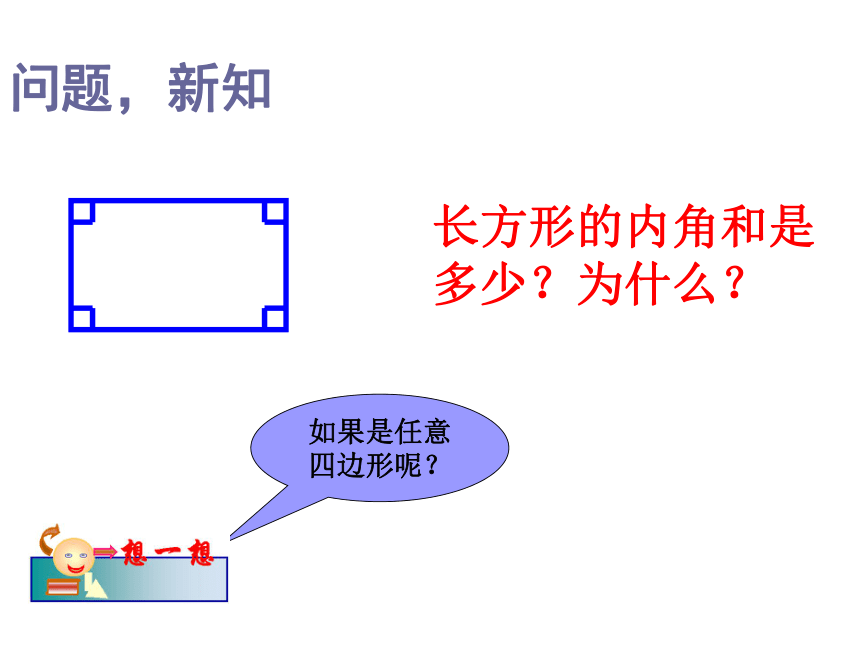
问题,新知
长方形的内角和是多少?为什么?
如果是任意四边形呢?
B
A
D
C
(1)四边形ABCD的内角 和是多少?
(2)你是怎样求的?
(1)从顶点A可以画几条对角线?分别是哪几条?
(2)这样五边形被分成了几个三角形?
(3)五边形的内角和是多少度?
A
B
D
C
E
你来探索六边形的内角和,你一定行!
A
B
C
D
E
F
被分得三角形个数
六边形的内角和
4
4×180°
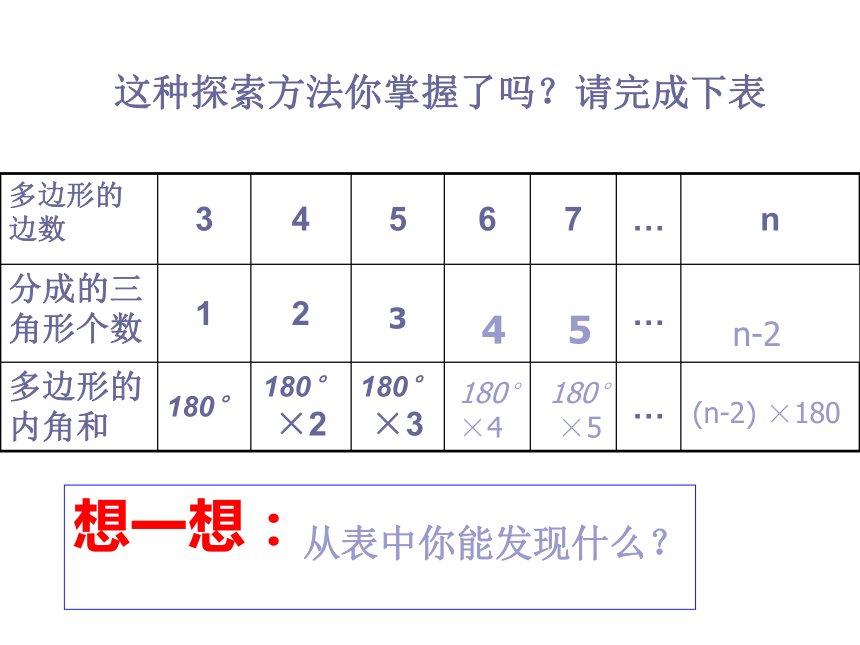
这种探索方法你掌握了吗?请完成下表
多边形的边数
3
4
5
6
7
…
n
分成的三角形个数
1
2
…
多边形的内角和
180°
180° ×2
180° ×3
…
3
4
5
n-2
180°
×5
(n-2) ×180
180° ×4
想一想:从表中你能发现什么?
多边形内角和公式:
n边形的内角和等于
(n-2).180°
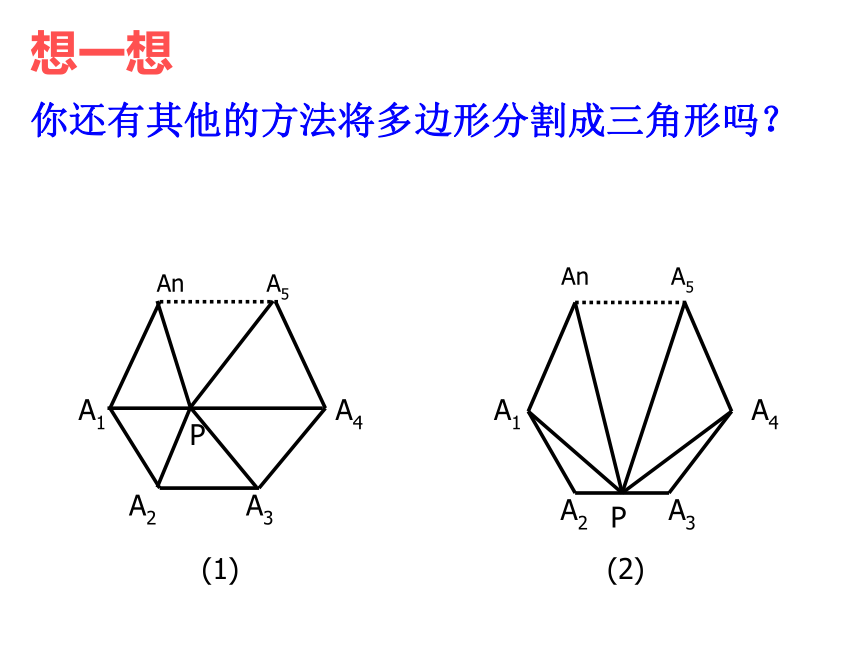
想一想
An A5
A1 A4
A2 A3
An A5
A1 A4
A2 A3
P
P
(1)
(2)
你还有其他的方法将多边形分割成三角形吗?
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
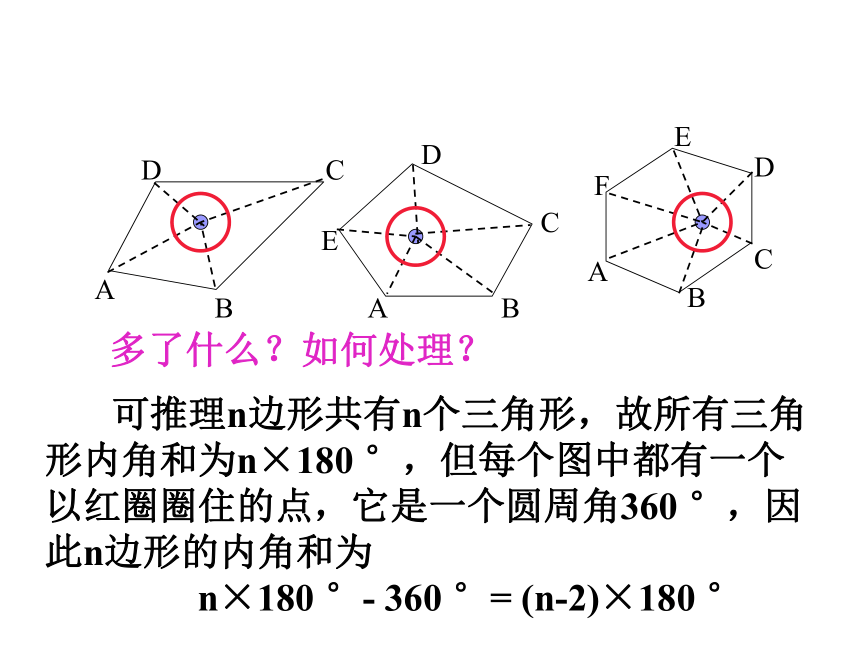
可推理n边形共有n个三角形,故所有三角形内角和为n×180 °,但每个图中都有一个以红圈圈住的点,它是一个圆周角360 °,因此n边形的内角和为
n×180 °- 360 °= (n-2)×180 °
多了什么?如何处理?
多了什么?如何处理?
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
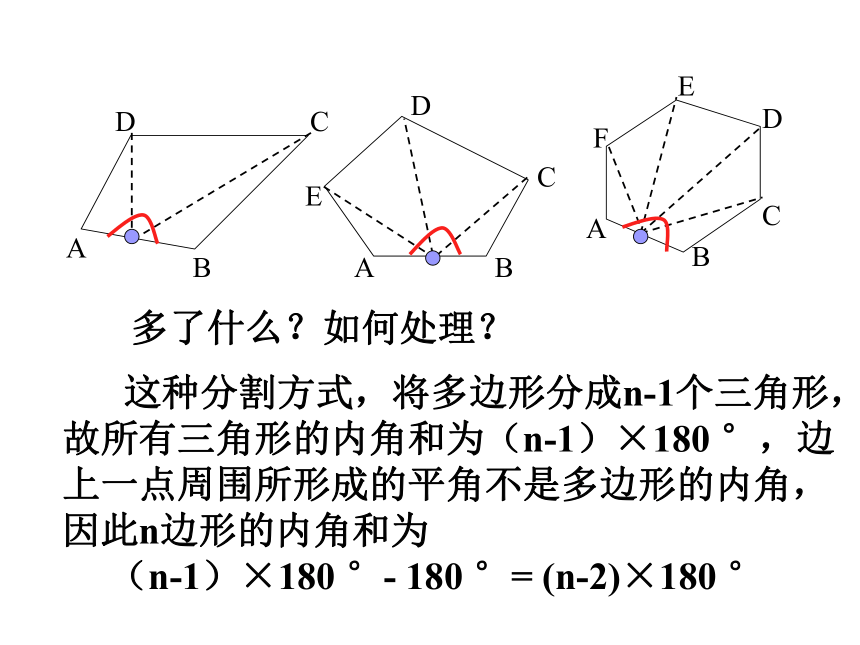
这种分割方式,将多边形分成n-1个三角形,故所有三角形的内角和为(n-1)×180 °,边上一点周围所形成的平角不是多边形的内角,因此n边形的内角和为
(n-1)×180 °- 180 °= (n-2)×180 °
例1:求八边形的内角和的度数。
解:(n-2)×180°=(8-2)×180°
=1080°
答:八边形的内角和为1080°。
牛刀小试:
(1)十边形的内角和等于 。
(2)已知一个多边形的内角和等于2340°,
它的边数是 。
(3)小明在计算多边形的内角和时求得的
度数是1000°,他的答案正确吗?为
什么?
1440°
15
问题
大家清晨跑步吗?小明就有每天坚持跑步的好习惯,他怎样跑步呢?右图就是小明清晨沿一个五边形广场周围的小跑,按逆时针方向跑步的效果图. 请你观察并思考如下几个问题:
(1)小明每从一条街道转到下一条街道时,身体转过的角是哪个角?在图中标出它们.
A
B
C
D
E
1
2
3
4
5
(2)他每跑完一圈,身体转过的角度之和是多少?
(3)在上图中,你能求出1+∠2+∠3+∠4+∠5的大小吗?你是怎样得到的?
探索
(1)什么是三角形的外角?外角有什么性质?
(2)类似地,在多边形中找出外角
多边形的一边与另一边的延长线的夹角,叫做多边形的外角。
做一做
(1)如图,求△ABC的三个外角的和。
三角形的三个外角之和为3600
(2)四边形的外角和等于多少度?
(3)五边形的外角和怎么求?n边形呢?
猜想与说理:
n边形的外角和是多少度呢?
答:都是360°.因为多边形的外角与它相邻的内角是邻补角,所以n边形的外角和加内角和等于n·180°,内角和为(n-2)·180°,因此,外角和为:n·180°-(n-2)·180°= 360°.
结论:多边形的外角和都等于360°.
例1:一个多边形的内角和等于它的外角和的3倍,它是几边形?
解:设它是n边形,则
(n-2).180=3×360
解得:n=8
答:它是8边形
例2:一个正多边形的每个内角比相邻外角大36°求这个多边形的边数。
解:设一个外角为x°,
则内角为(x+36)°
根据题意得:
x+x+36=180
x=72
360÷72=5
答:这个正多边形为正五边形。
(1)一个多边形的每一个外角都是600,这个多边形是几边形?它的内角和等于多少度?
(2)有没有这样的多边形,它的内角和是外角和的3倍?
(3)一个多边形的每一个外角都相等,且每一个内角都比外角大900,求这个多边形的边数和每个内角的度数。
7、两个多边形的边数比是1:2,两个多边形的内角和为1440度,求这两个多边形的边数,
6、一个多边形的每个内角都比相邻的外角3倍多20度,求这个多边形的边数,
5、四边形的四个内角的比是8:6:3:7,求它的四个内角,
4、一个多边形的内角和是外角和的4倍,这是几边形
三角形三个内角的度数分别是(x+y)o, (x-y)o,xo,且x>y>0,则该三角形有一个内角为 ( )
A、30O B、45O C、60O D、90O
2.一个正多边形每一个内角都是120o,这个多边形是( ) A、正四边形 B、正五边形
C、正六边形 D、正七边形
C
C
3.一个多边形木板,截去一个三角形后(截线不经过顶点),得到新多边形内角和为2160o,则原多边形的边数为( )
A、13条 B、14条 C、15条 D、16条
下列说法中,错误的是( )
A、一个三角形中至少有一个角不大于60O; B、有一个外角是锐角的三角形是钝角三角形;C、三角形的外角中必有两个角是钝角; D、锐角三角形中两锐角的和必然小于60O;
A
D
5.小明绕五边形各边走一圈,他共转了_ __度。
6.下列正多边形(1)正三角形(2)正方形(3)正五边形(4)正六边形,其中用一种正多边形能镶嵌成平面图案的是 ;
360
(1)、(2)、(4)
7.如下图,AD是BC边上的高,BE是 △ ABD的角平分线,∠1=40°,∠2=30°,则∠C=_ __∠BED= 。
65°
60°
A
B
C
D
1
2
E
8、两个多边形的边数比是1:2,两个多边形的内角和为1440度,求这两个多边形的边数,
9、有一六边形,截去一三角形,内角和会发生
怎样变化?请画图说明。
内角和减少180O
内角和不变
内角和增加180O
把一个五边形切取一个角,将得到几边形?此时多边形的内角与外角有什么变化?
探究活动:
A
B
C
D
如图, ∠A=45°, ∠B=25 ° ∠C=30 ° ,则 ∠D= 。
E
E
100 °
探究活动:
A
B
C
D
如图, ∠A+∠B+∠C+∠E+∠F= 。
E
F
G
180 °
G
探究活动:
A
B
C
D
如图, ∠A+∠B+∠C+∠E+∠F= 。
E
F
1
2
3
4
5
180 °
巩固一下:
求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数。
A
G
F
E
D
C
B
7×180O-2×360O=540O
(4)求∠A+∠B+∠C+∠D+∠E+∠F的度数。
华岩教育课程辅导中心(济源)
常年招收初中各年级一对一、一对多、小班学生
招生学科:英语、数学、物理、化学、地理、生物
学习环境:
1、夏季空调、冬季市政供暖全天候开放
2、免费矿泉水全天候供应
您还可以免费享受到我们以下周到的服务:
1、免费试听三次(三次课以内无论任何理由离开我处,均不需要交
纳任何费用)
2、免费提供相关学习资料
3、免费咨询学习、心理等各方面信息
4、免费不定期开设家长课程,讲授中学生心理和家庭教育相关知识
上课地点:河南省济源市世纪广场南侧华新东区(华新花园)
详情咨询:18603892560 联 系 人:梁老师
例:如果一个四边形一组对角互补,那么另一组对角有什么关系?
A
B
C
D
例题、已知两个多边形的内角和为1440°,且两多边形的边数之比为1︰3,求它们的边数分别是多少?
解:设它们的边数分别是x,y.由题意得:
(x-2)·180+( y -2)·180=1440
x : y=1 : 3
解之得 x =3
y =9
答:它们的边数分别是3和9。
1、在平面内, _____________________ 叫做多边形。
2、在多边形中连接 _________________ 的线段叫做多边形的对角线。
3、三角形的内角和是_____度.
4、你能够利用三角形的内角和求四边形的内角和吗?试试看?
思路:多边形问题转化为三角形问题来解决.
由一些线段首尾顺次相接组成的图形
多边形不相邻的两个顶点的线段
1800
问题,新知
长方形的内角和是多少?为什么?
如果是任意四边形呢?
B
A
D
C
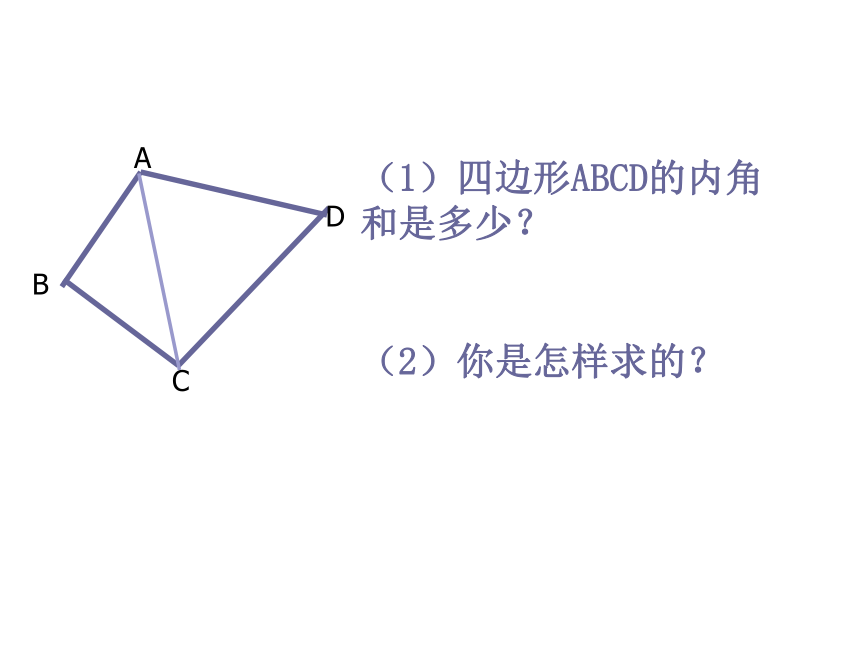
(1)四边形ABCD的内角 和是多少?
(2)你是怎样求的?
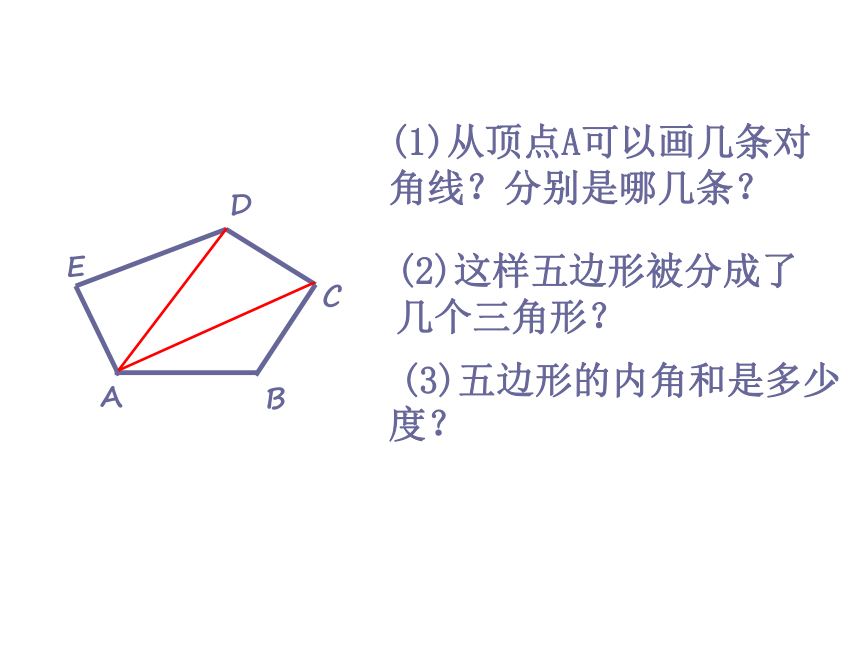
(1)从顶点A可以画几条对角线?分别是哪几条?
(2)这样五边形被分成了几个三角形?
(3)五边形的内角和是多少度?
A
B
D
C
E
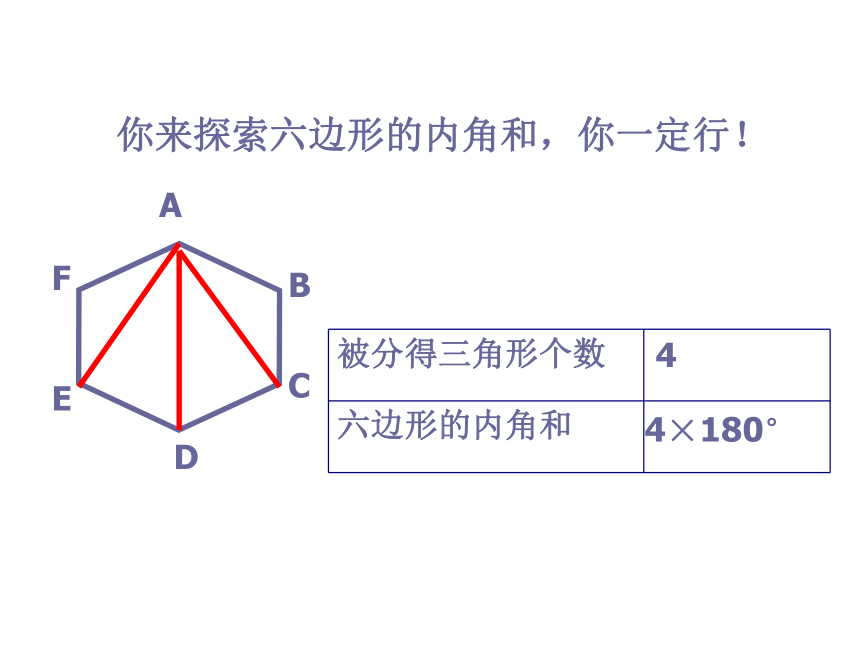
你来探索六边形的内角和,你一定行!
A
B
C
D
E
F
被分得三角形个数
六边形的内角和
4
4×180°
这种探索方法你掌握了吗?请完成下表
多边形的边数
3
4
5
6
7
…
n
分成的三角形个数
1
2
…
多边形的内角和
180°
180° ×2
180° ×3
…
3
4
5
n-2
180°
×5
(n-2) ×180
180° ×4
想一想:从表中你能发现什么?
多边形内角和公式:
n边形的内角和等于
(n-2).180°
想一想
An A5
A1 A4
A2 A3
An A5
A1 A4
A2 A3
P
P
(1)
(2)
你还有其他的方法将多边形分割成三角形吗?
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
可推理n边形共有n个三角形,故所有三角形内角和为n×180 °,但每个图中都有一个以红圈圈住的点,它是一个圆周角360 °,因此n边形的内角和为
n×180 °- 360 °= (n-2)×180 °
多了什么?如何处理?
多了什么?如何处理?
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
这种分割方式,将多边形分成n-1个三角形,故所有三角形的内角和为(n-1)×180 °,边上一点周围所形成的平角不是多边形的内角,因此n边形的内角和为
(n-1)×180 °- 180 °= (n-2)×180 °
例1:求八边形的内角和的度数。
解:(n-2)×180°=(8-2)×180°
=1080°
答:八边形的内角和为1080°。
牛刀小试:
(1)十边形的内角和等于 。
(2)已知一个多边形的内角和等于2340°,
它的边数是 。
(3)小明在计算多边形的内角和时求得的
度数是1000°,他的答案正确吗?为
什么?
1440°
15
问题
大家清晨跑步吗?小明就有每天坚持跑步的好习惯,他怎样跑步呢?右图就是小明清晨沿一个五边形广场周围的小跑,按逆时针方向跑步的效果图. 请你观察并思考如下几个问题:
(1)小明每从一条街道转到下一条街道时,身体转过的角是哪个角?在图中标出它们.
A
B
C
D
E
1
2
3
4
5
(2)他每跑完一圈,身体转过的角度之和是多少?
(3)在上图中,你能求出1+∠2+∠3+∠4+∠5的大小吗?你是怎样得到的?
探索
(1)什么是三角形的外角?外角有什么性质?
(2)类似地,在多边形中找出外角
多边形的一边与另一边的延长线的夹角,叫做多边形的外角。
做一做
(1)如图,求△ABC的三个外角的和。
三角形的三个外角之和为3600
(2)四边形的外角和等于多少度?
(3)五边形的外角和怎么求?n边形呢?
猜想与说理:
n边形的外角和是多少度呢?
答:都是360°.因为多边形的外角与它相邻的内角是邻补角,所以n边形的外角和加内角和等于n·180°,内角和为(n-2)·180°,因此,外角和为:n·180°-(n-2)·180°= 360°.
结论:多边形的外角和都等于360°.
例1:一个多边形的内角和等于它的外角和的3倍,它是几边形?
解:设它是n边形,则
(n-2).180=3×360
解得:n=8
答:它是8边形
例2:一个正多边形的每个内角比相邻外角大36°求这个多边形的边数。
解:设一个外角为x°,
则内角为(x+36)°
根据题意得:
x+x+36=180
x=72
360÷72=5
答:这个正多边形为正五边形。
(1)一个多边形的每一个外角都是600,这个多边形是几边形?它的内角和等于多少度?
(2)有没有这样的多边形,它的内角和是外角和的3倍?
(3)一个多边形的每一个外角都相等,且每一个内角都比外角大900,求这个多边形的边数和每个内角的度数。
7、两个多边形的边数比是1:2,两个多边形的内角和为1440度,求这两个多边形的边数,
6、一个多边形的每个内角都比相邻的外角3倍多20度,求这个多边形的边数,
5、四边形的四个内角的比是8:6:3:7,求它的四个内角,
4、一个多边形的内角和是外角和的4倍,这是几边形
三角形三个内角的度数分别是(x+y)o, (x-y)o,xo,且x>y>0,则该三角形有一个内角为 ( )
A、30O B、45O C、60O D、90O
2.一个正多边形每一个内角都是120o,这个多边形是( ) A、正四边形 B、正五边形
C、正六边形 D、正七边形
C
C
3.一个多边形木板,截去一个三角形后(截线不经过顶点),得到新多边形内角和为2160o,则原多边形的边数为( )
A、13条 B、14条 C、15条 D、16条
下列说法中,错误的是( )
A、一个三角形中至少有一个角不大于60O; B、有一个外角是锐角的三角形是钝角三角形;C、三角形的外角中必有两个角是钝角; D、锐角三角形中两锐角的和必然小于60O;
A
D
5.小明绕五边形各边走一圈,他共转了_ __度。
6.下列正多边形(1)正三角形(2)正方形(3)正五边形(4)正六边形,其中用一种正多边形能镶嵌成平面图案的是 ;
360
(1)、(2)、(4)
7.如下图,AD是BC边上的高,BE是 △ ABD的角平分线,∠1=40°,∠2=30°,则∠C=_ __∠BED= 。
65°
60°
A
B
C
D
1
2
E
8、两个多边形的边数比是1:2,两个多边形的内角和为1440度,求这两个多边形的边数,
9、有一六边形,截去一三角形,内角和会发生
怎样变化?请画图说明。
内角和减少180O
内角和不变
内角和增加180O
把一个五边形切取一个角,将得到几边形?此时多边形的内角与外角有什么变化?
探究活动:
A
B
C
D
如图, ∠A=45°, ∠B=25 ° ∠C=30 ° ,则 ∠D= 。
E
E
100 °
探究活动:
A
B
C
D
如图, ∠A+∠B+∠C+∠E+∠F= 。
E
F
G
180 °
G
探究活动:
A
B
C
D
如图, ∠A+∠B+∠C+∠E+∠F= 。
E
F
1
2
3
4
5
180 °
巩固一下:
求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数。
A
G
F
E
D
C
B
7×180O-2×360O=540O
(4)求∠A+∠B+∠C+∠D+∠E+∠F的度数。
华岩教育课程辅导中心(济源)
常年招收初中各年级一对一、一对多、小班学生
招生学科:英语、数学、物理、化学、地理、生物
学习环境:
1、夏季空调、冬季市政供暖全天候开放
2、免费矿泉水全天候供应
您还可以免费享受到我们以下周到的服务:
1、免费试听三次(三次课以内无论任何理由离开我处,均不需要交
纳任何费用)
2、免费提供相关学习资料
3、免费咨询学习、心理等各方面信息
4、免费不定期开设家长课程,讲授中学生心理和家庭教育相关知识
上课地点:河南省济源市世纪广场南侧华新东区(华新花园)
详情咨询:18603892560 联 系 人:梁老师
例:如果一个四边形一组对角互补,那么另一组对角有什么关系?
A
B
C
D
例题、已知两个多边形的内角和为1440°,且两多边形的边数之比为1︰3,求它们的边数分别是多少?
解:设它们的边数分别是x,y.由题意得:
(x-2)·180+( y -2)·180=1440
x : y=1 : 3
解之得 x =3
y =9
答:它们的边数分别是3和9。
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
