北师大版八年级下册数学 2.2 不等式的基本性质 课件(共24张PPT)
文档属性
| 名称 | 北师大版八年级下册数学 2.2 不等式的基本性质 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 700.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 21:05:28 | ||
图片预览







文档简介
§2.2 不 等 式的基本性质
学习目标:
1.探索并掌握不等式的基本性质,并运用它对不等式进行变形.
2.理解不等式性质与等式性质的联系与区别.
3.提高观察、比较、归纳的能力,渗透类比的思想方法.
学习重难点:
重点:探索不等式的基本性质,并能灵活地掌握和应用.
难点:能根据不等式的基本性质进行化简.
温故知新
观察下面两组式子:
第一组:1+2=3; a+b=b+a; S = ab; 4+x = 7.
第二组:-7 < -5; 3+4 > 1+4; 2x ≤6,
a+2 ≥0; 3≠4.
第一组都是 ,第二组是
等式
不等式
2、判断下列式子是不是不等式:
(1)-3<0; (2)4x+3y>0
(3)x=3; (4) X2+xy+y2
(5)x≠5; (6)X+2>y+5;
1、像-7 < -5; 3+4 > 1+4; 2x ≤6,a+2 ≥0; 3≠4等表示不等关系的式子叫做不等式
知识点一:不等式
等式的基本性质
等式的两边都加上(或减去)同一个数或同一个整式,所得的结果仍是等式.
(2)等式的两边都乘以(或除以)同一个数(除数不能为零),所得的结果仍是等式.
若a=b,则a+c=b+c (或a-c=b-c)
若a=b,则ac=bc 或 ,c≠0)
c
a
=
b
c
知识联想
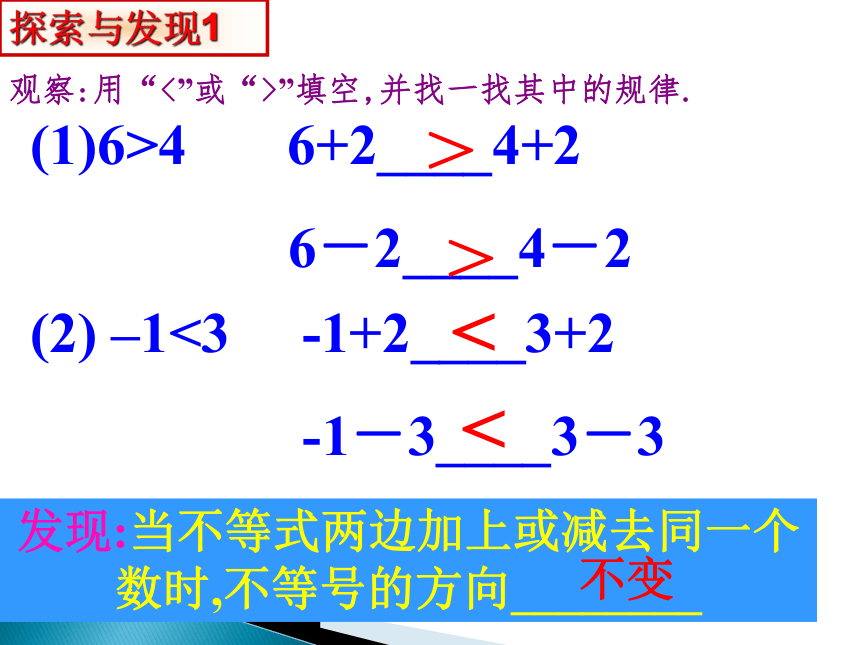
观察:用“<”或“>”填空,并找一找其中的规律.
(2) –1<3 -1+2____3+2
-1-3____3-3
6>4 6+2____4+2
6-2____4-2
>
>
<
<
发现:当不等式两边加上或减去同一个数时,不等号的方向________
不变
探索与发现1
如果a>b,那么a+c b+c, a-c b-c.
如果a<b,那么a+c b+c, a-c b-c;
>
>
<
<
知识点二:不等式的基本性质1
不等式两边都加(或减去)
同一个数(或者同一个整式),不等号的方向不变.
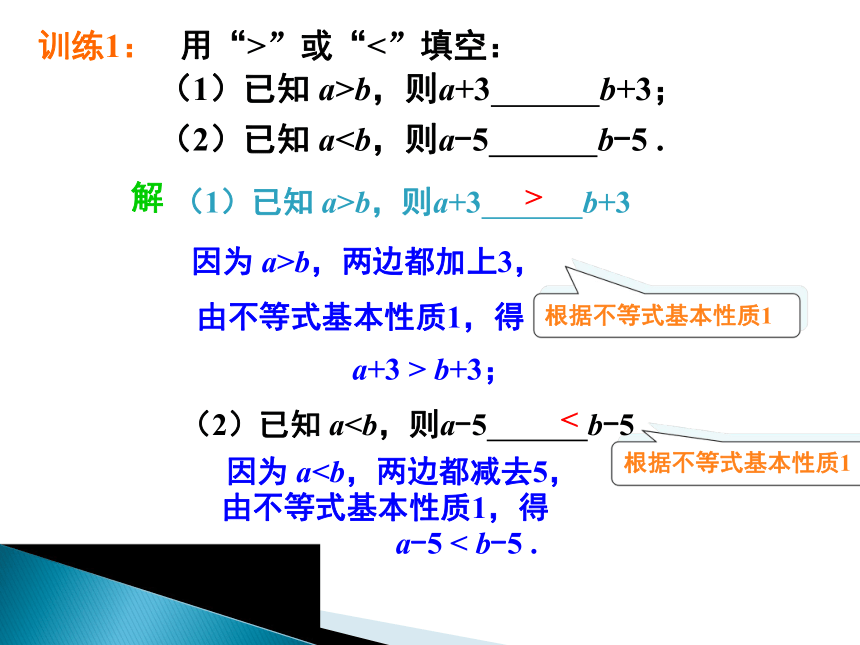
因为 a>b,两边都加上3,
因为 a解
由不等式基本性质1,得
a+3 > b+3;
根据不等式基本性质1
由不等式基本性质1,得
a-5 < b-5 .
根据不等式基本性质1
(1)已知 a>b,则a+3 b+3
(2)已知 a>
<
训练1: 用“>”或“<”填空:
(1)已知 a>b,则a+3 b+3;
(2)已知 a练习
训练2: 1. 已知a < b,用“>”或“<”填空:
(1)a +12 b +12 ;
(2)b -10 a -10 .
<
>
已知4<6,则
4×2 6×2;
4÷2 6÷2;
<
<
探索与发现2
知识点三:
不等式的基本性质2
不等式的两边都乘(或都除以)同一个正数,不等号的方向不变。
如果a>b,且c>0,那么ac>bc
不等式的两边都乘以(或都除以)同一个负数,不等号的方向改变.
如果a>b,且c<0,那么ac<bc,
知识点四:
不等式的基本性质3
不等式两边都乘(或除以)一个不为零的数,不等号方向改不改变和什么有关?
当不等式的两边同乘(或除以)同一个正数时,不等号的方向_____;而乘(或除以)同一个负数时,不等号的方向____.
思考
不变
改变
训练3: 用“>”或“<”填空:
举
例
(1)已知 a>b,则3a 3b ;
(2)已知 a>b,则-a -b .
(3)已知 a不等式的性质1 不等式两边加上(或减去)同一个数(或整式),不等号的方向不变.
不等式的性质2 不等式两边乘以(或除以)同一个正数,不等号的方向不变.
不等式的性质3 不等式两边乘以(或除以)同一个负数,不等号的方向改变.
变!
判断对错并说明理由
1. 若 -3<0, 则 -3+1<1 ( )
2. 若 -3 × 2> -5 ×2, 则 -3< -5 ( )
3. 若 a4. 若 -6a < -6 b, 则 a < b ( )
√
×
知识应用1
√
×
判断对错并说明理由
√
×
知识应用2
√
×
5. 若 a>b, 则-a < -b ( )
6. 若 -2x >0, 则 x > 0 ( )
7. 若 -2<1, 则 -2a < a ( )
8. 若 a >0, 则 3a > 2a ( )
解 (1)根据不等式的性质1,两边都加上7得:
x-7+7 > 2+7
即 x > 9
(2)根据不等式的性质1,两边都减去5 x 得:
6 x -5 x <(5 x -1)-5 x
即 x <-1
例 1 根据不等式的基本性质,把下列不等式化成 x< 或 x> 的形式:
(1) x -7 > 2 (2) 6 x < 5 x -1
(3)4x-5< 5x (4) - x < -1
典例解析
从变形前后的两个不等式可以看出,这种变形就是把不等式一边的某一项变号后移到另一边,我们把这种变形称为移项.
例2:已知x>y,试比较-2x和-2y的大小,并说明理由
变式4:若x>y,比较(a-3)x与(a-3)y的大小?
典例解析
变式1:比较a-2x和a-2y的大小
变式3: 若x>y,且(a-3)x<(a-3)y,求a的取值范围。
变式2:比较 和 的大小
训练4:用“>”或“<” 填空:
(1)如果1-x>3,那么x -2 ;
<
(2)如果 x+2<3x+8,那么 x -3.
>
训练5:说出下列不等式的变形是根据不等式的
哪一条基本性质?
2.已知m(a-3)n,求a的范围.
1.已知x>y,比较2-3x与2-3y的大小.
先×(-3),再+2
先×(-3),再+2
×(a-3)
×(a-3)
<
>
拓展延伸
解: 由题意可得:a-3<0(不等式的基本性质3)
∴a<3(不等式的基本性质2)
达标检测
不等式的三条性质是:
① 、不等式的两边都加上(或减去)同一个 数或同一个整式,不等号的方向不变;
② 、不等式的两边都乘以(或除以)同一个 正数,不等号的方向不变;
③ 、*不等式的两边都乘以(或除以)同一个负数,不等号的方向要改变 ;
小结
本节重点
(1)掌握不等式的三条性质,尤其是性质3;
(2)能正确应用性质对不等式进行变形;
学习目标:
1.探索并掌握不等式的基本性质,并运用它对不等式进行变形.
2.理解不等式性质与等式性质的联系与区别.
3.提高观察、比较、归纳的能力,渗透类比的思想方法.
学习重难点:
重点:探索不等式的基本性质,并能灵活地掌握和应用.
难点:能根据不等式的基本性质进行化简.
温故知新
观察下面两组式子:
第一组:1+2=3; a+b=b+a; S = ab; 4+x = 7.
第二组:-7 < -5; 3+4 > 1+4; 2x ≤6,
a+2 ≥0; 3≠4.
第一组都是 ,第二组是
等式
不等式
2、判断下列式子是不是不等式:
(1)-3<0; (2)4x+3y>0
(3)x=3; (4) X2+xy+y2
(5)x≠5; (6)X+2>y+5;
1、像-7 < -5; 3+4 > 1+4; 2x ≤6,a+2 ≥0; 3≠4等表示不等关系的式子叫做不等式
知识点一:不等式
等式的基本性质
等式的两边都加上(或减去)同一个数或同一个整式,所得的结果仍是等式.
(2)等式的两边都乘以(或除以)同一个数(除数不能为零),所得的结果仍是等式.
若a=b,则a+c=b+c (或a-c=b-c)
若a=b,则ac=bc 或 ,c≠0)
c
a
=
b
c
知识联想
观察:用“<”或“>”填空,并找一找其中的规律.
(2) –1<3 -1+2____3+2
-1-3____3-3
6>4 6+2____4+2
6-2____4-2
>
>
<
<
发现:当不等式两边加上或减去同一个数时,不等号的方向________
不变
探索与发现1
如果a>b,那么a+c b+c, a-c b-c.
如果a<b,那么a+c b+c, a-c b-c;
>
>
<
<
知识点二:不等式的基本性质1
不等式两边都加(或减去)
同一个数(或者同一个整式),不等号的方向不变.
因为 a>b,两边都加上3,
因为 a
由不等式基本性质1,得
a+3 > b+3;
根据不等式基本性质1
由不等式基本性质1,得
a-5 < b-5 .
根据不等式基本性质1
(1)已知 a>b,则a+3 b+3
(2)已知 a
<
训练1: 用“>”或“<”填空:
(1)已知 a>b,则a+3 b+3;
(2)已知 a
训练2: 1. 已知a < b,用“>”或“<”填空:
(1)a +12 b +12 ;
(2)b -10 a -10 .
<
>
已知4<6,则
4×2 6×2;
4÷2 6÷2;
<
<
探索与发现2
知识点三:
不等式的基本性质2
不等式的两边都乘(或都除以)同一个正数,不等号的方向不变。
如果a>b,且c>0,那么ac>bc
不等式的两边都乘以(或都除以)同一个负数,不等号的方向改变.
如果a>b,且c<0,那么ac<bc,
知识点四:
不等式的基本性质3
不等式两边都乘(或除以)一个不为零的数,不等号方向改不改变和什么有关?
当不等式的两边同乘(或除以)同一个正数时,不等号的方向_____;而乘(或除以)同一个负数时,不等号的方向____.
思考
不变
改变
训练3: 用“>”或“<”填空:
举
例
(1)已知 a>b,则3a 3b ;
(2)已知 a>b,则-a -b .
(3)已知 a
不等式的性质2 不等式两边乘以(或除以)同一个正数,不等号的方向不变.
不等式的性质3 不等式两边乘以(或除以)同一个负数,不等号的方向改变.
变!
判断对错并说明理由
1. 若 -3<0, 则 -3+1<1 ( )
2. 若 -3 × 2> -5 ×2, 则 -3< -5 ( )
3. 若 a
√
×
知识应用1
√
×
判断对错并说明理由
√
×
知识应用2
√
×
5. 若 a>b, 则-a < -b ( )
6. 若 -2x >0, 则 x > 0 ( )
7. 若 -2<1, 则 -2a < a ( )
8. 若 a >0, 则 3a > 2a ( )
解 (1)根据不等式的性质1,两边都加上7得:
x-7+7 > 2+7
即 x > 9
(2)根据不等式的性质1,两边都减去5 x 得:
6 x -5 x <(5 x -1)-5 x
即 x <-1
例 1 根据不等式的基本性质,把下列不等式化成 x< 或 x> 的形式:
(1) x -7 > 2 (2) 6 x < 5 x -1
(3)4x-5< 5x (4) - x < -1
典例解析
从变形前后的两个不等式可以看出,这种变形就是把不等式一边的某一项变号后移到另一边,我们把这种变形称为移项.
例2:已知x>y,试比较-2x和-2y的大小,并说明理由
变式4:若x>y,比较(a-3)x与(a-3)y的大小?
典例解析
变式1:比较a-2x和a-2y的大小
变式3: 若x>y,且(a-3)x<(a-3)y,求a的取值范围。
变式2:比较 和 的大小
训练4:用“>”或“<” 填空:
(1)如果1-x>3,那么x -2 ;
<
(2)如果 x+2<3x+8,那么 x -3.
>
训练5:说出下列不等式的变形是根据不等式的
哪一条基本性质?
2.已知m
1.已知x>y,比较2-3x与2-3y的大小.
先×(-3),再+2
先×(-3),再+2
×(a-3)
×(a-3)
<
>
拓展延伸
解: 由题意可得:a-3<0(不等式的基本性质3)
∴a<3(不等式的基本性质2)
达标检测
不等式的三条性质是:
① 、不等式的两边都加上(或减去)同一个 数或同一个整式,不等号的方向不变;
② 、不等式的两边都乘以(或除以)同一个 正数,不等号的方向不变;
③ 、*不等式的两边都乘以(或除以)同一个负数,不等号的方向要改变 ;
小结
本节重点
(1)掌握不等式的三条性质,尤其是性质3;
(2)能正确应用性质对不等式进行变形;
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
