北师大版八年级下册数学 2.5一元一次不等式和一次函数 课件 (共25张PPT)
文档属性
| 名称 | 北师大版八年级下册数学 2.5一元一次不等式和一次函数 课件 (共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 267.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 20:55:47 | ||
图片预览





文档简介
2.5 一元一次不等式与一次函数
一)回顾与思考
1.如果y=kx+b(k,b是常数,k≠0),那么y叫做x的_______。
2.一次函数y=kx+b(k≠0) 的图象是________
3.一次函数y=kx+b(k≠0),当y>0时,则kx+b__0;当y<0时,则kx+b__0.
4.一次函数y=2x-6,当x___时,y>0
5.已知一次函数y1=-x-4,y2=3x+5,当x___时,y1< y2
6.一次函数y=kx+b(k≠0)与坐标轴交点坐标的求法;
练一练:
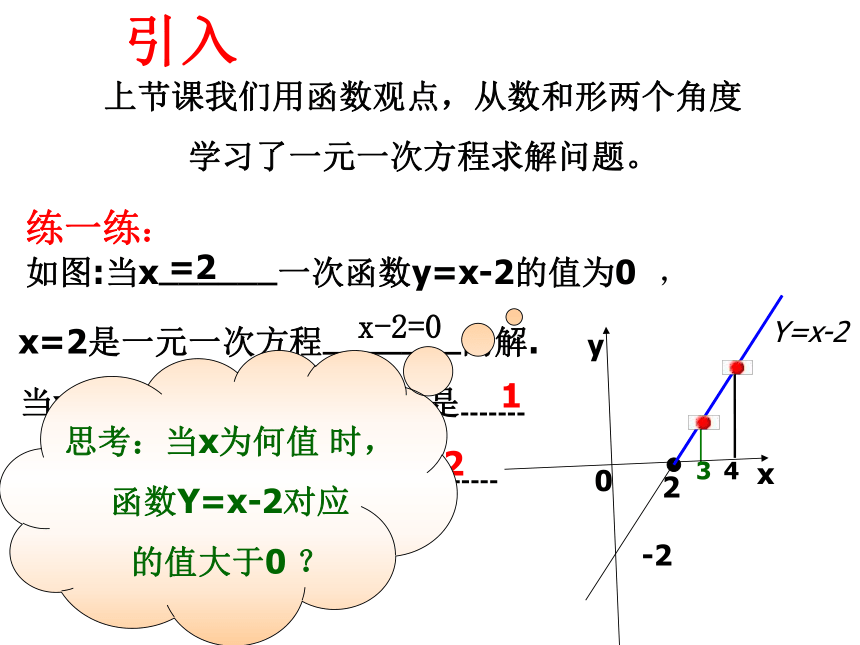
如图:当x——————一次函数y=x-2的值为0 ,
引入
x=2是一元一次方程———————的解.
=2
x-2=0
3
2
x
-2
y
0
Y=x-2
4
当x=3时,函数y=x-2的值是-------
1
当x=4,函数y=x-2的值是--------
2
思考:当x为何值 时,
函数Y=x-2对应
的值大于0 ?
上节课我们用函数观点,从数和形两个角度
学习了一元一次方程求解问题。
思考:
(1)问题1与问题2有什么关系?
两个问题实际上是同一个问题,虽然结果一样,
但是表达的方式不同。因为问题1是直接求不等式2x-4 >0的解集,解得X>2,是从不等式角度进行求解。而问题2是考虑当函数 y=2x-4的函数值大于0时,自变量X的取值,是通过列不等式2x-4 > 0求解,解得X>2,是从函数的角度进行求解。
问题2:
自变量为何值时,函数y=2x-4的值大于0?
问题1:解不等式2x-4>0
探究:
我们从函数图象来看看
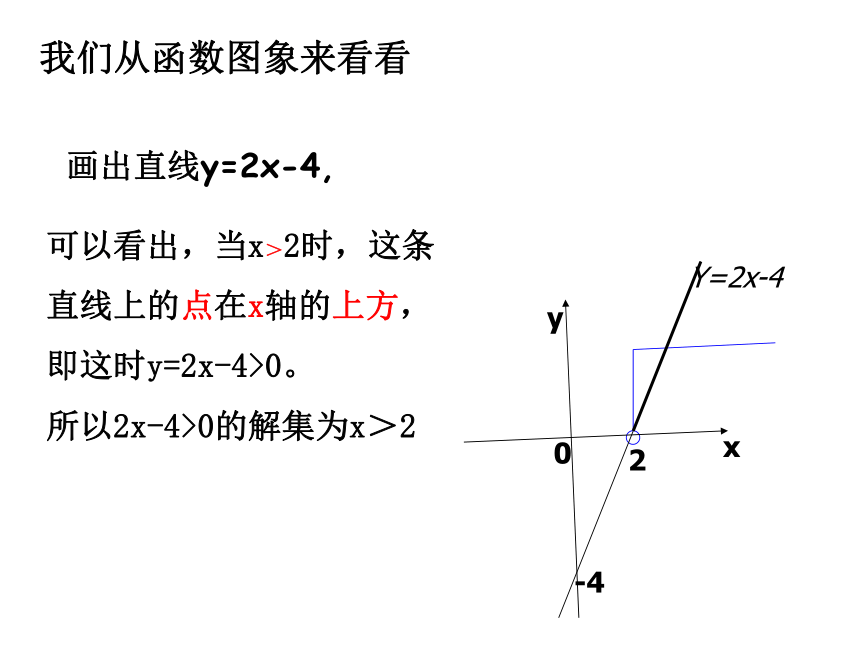
画出直线y=2x-4,
-4
2
y
x
0
Y=2x-4
可以看出,当x>2时,这条
直线上的点在x轴的上方,
即这时y=2x-4>0。
所以2x-4>0的解集为x>2
试一试(根据一次函数与不等式的关系填空):
求一次函数y=3x-6的函数值
小于0的自变量的取值范围。
求不等式3x+8>0的解集。
(1) 解不等式3x-6<0,可看作
(2)“当自变量x取何值时,函数y=3x+8的值大于0”可看作
-2
x
y=3x+6
y
例 根据下列一次函数的图像,直接写出下列不等式的解集
3x+6>0
(3) –x+3 ≥0
x
y
3
y=-x+3
(2)3x+6 ≤0
X>-2
(4) –x+3<0
x≤3
X≤-2
x>3
(即y>0)
(即y≤0)
(即y<0)
(即y≥0)
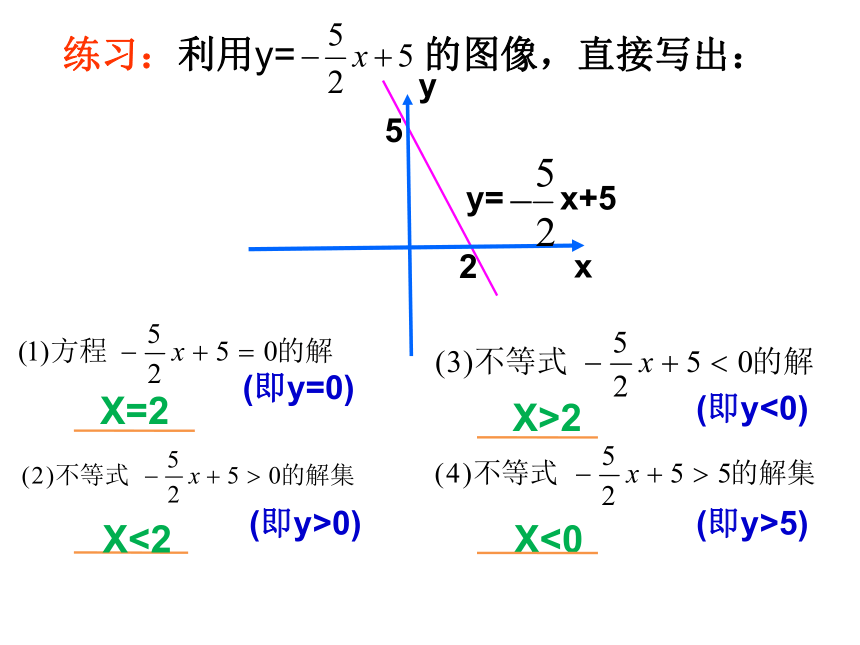
练习:利用y= 的图像,直接写出:
y
2
5
x
y= x+5
X=2
X<2
X>2
X<0
(即y=0)
(即y>0)
(即y<0)
(即y>5)
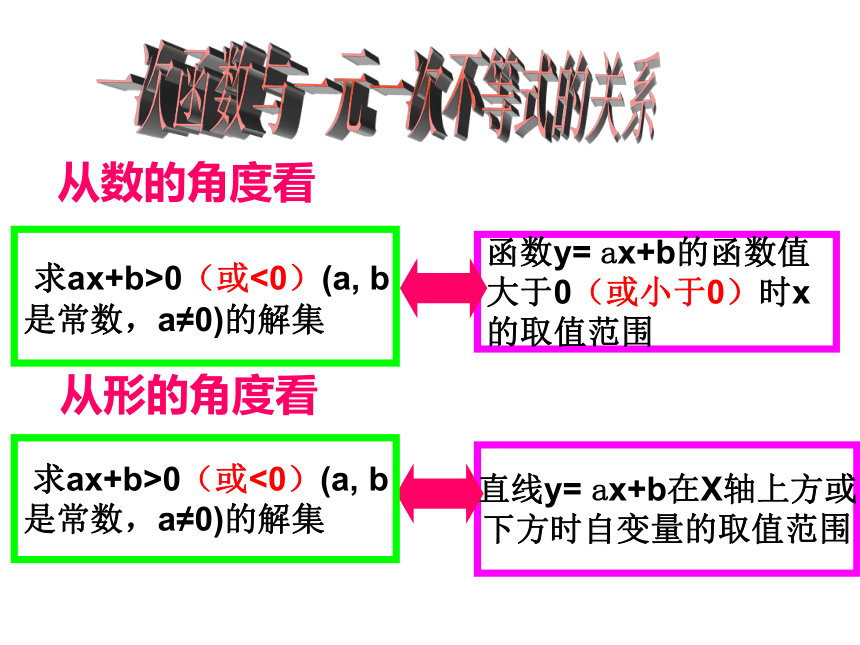
一次函数与一元一次不等式的关系
求ax+b>0(或<0)(a, b
是常数,a≠0)的解集
函数y= ax+b的函数值
大于0(或小于0)时x
的取值范围
直线y= ax+b在X轴上方或
下方时自变量的取值范围
从数的角度看
从形的角度看
求ax+b>0(或<0)(a, b
是常数,a≠0)的解集
可以看出,当x<2时这条直线上的点在x轴的下方,
解法一:化简得3x-6<0,画出直线y=3x-6,
即这时y=3x-6<0,所以不等式的解集为x<2
例1.用画函数图象的方法解不等式 5x+4<2x+10
y
x
-6
2
0
Y=3x-6
尝试:
解法二:画出函数 y = 2x+10 y = 5x+4图象
从图中看出:当x <2时
直线 y = 5x +4 在 y = 2x +10的下方
即 5x+4 < 2x +10
∴ 不等式 5x+4 < 2 x +10 的解集是
x < 2
Y1=5x+4
y
x
0
Y2=2X+10
2
-2
当堂检测
完成 “当堂检测”
当堂检测
1.如图是一次函数
的图象,则关于x的方程
的解为 ;关于x的不等式
的解集为 ;
的解集为 .
关于x的不等式
当堂检测
2.若关于x的不等式
的解集为
则一次函数
当
时,图象在
时,图象在x轴______.
x轴_________;当
分析:可以画出函数草图进行解答
当堂检测
3.如右图, 一次函数
的图象
经过点 ,则关于x的不等式 的解集为________________.
分析:即求y>-2时x的取值范围
当堂检测
4、看图象说不等式
的解集
x
o
y=5x-3
2
y=3x+1
7
y
当堂检测
x>2
1.如图是一次函数
的图象,则关于x的方程
的解为 ;关于x的不等式
的解集为 ;
的解集为 .
关于x的不等式
x=2
x<2
当堂检测
下方
2.若关于x的不等式
的解集为
则一次函数
当
时,图象在
时,图象在x轴______.
x轴_________;当
上方
分析:可以画出函数草图进行解答
当堂检测
3.如右图, 一次函数
的图象
经过点 ,则关于x的不等式 的解集为________________.
x<-2
分析:即求y>-2时x的取值范围
当堂检测
4、看图象解不等式
x
o
y=5x-3
2
y=3x+1
7
y
从图中看出,当x>2时,直线y=5x-3上的点在直线y=3x+1上相应点的上方,即5x-3>3x+1,所以不等式的解集为x>2。
1.这节课我们学到了哪些知识?
2.我们是用哪些方法获得这些知识的?
3.你觉得还有什么问题需要继续讨论吗?
回顾 反思
求一元一次不等式的解,可以看成某一个一次函数当自变量取何值时,函数的值大于零或等于零。
2、如图,直线L1, L2交于一点P,若y1 ≥y2 ,则( )
x ≥ 3
x ≤3
2 ≤ x ≤ 3
x ≤ 4
1、已知函数Y=3X+8,当X————————,函数
的值等于0。当X————————,函数的值大于0。当X———————— ,函数的值不大于2。
=
≤- 2
>
B
做一做
3.利用函数图象解不等式:3x-4<x+2(用两种方法)
解法1:化简不等式得2x-6<0,画出函数y=2x-6的图象。
当x<3时y=2x-6<0,所以不等式的解集为x<3。
解法2:画出函数y=3x-4和函数y=x+2的图象,交点横坐标为3。
当x<3时,对于同一个x,直线y=3x-4上的点在直线y=x+2上相应点的下方,这表示3x-4<x+2,所以不等式的解集为x< 3。
y
x
0
-6
3
Y=2x-6
3
y
x
0
y=x+2
y=3x-4
1、某单位准备和一个体车主或一国营出租车公司中的一家签订月租车合同,设汽车每月行驶x 千米,个体车主收费y1元,国营出租车公司收费为y2元,观察下列图象可知(如图1-5-2),当x________时,选用个体车较合算.
课后思考
我们学校做一批校徽,需要拍照,若到照相馆拍,每张需要8元;若学校自己拍,除买摄象机,需120元,每张还需成本4元,设需要拍X张,到照相馆拍需要Y1 元,学校自己拍需要Y2元。
1.求Y1和Y2与X的函数关系式
2.问拍这批照片到照相馆拍,费用省还是由学校自己拍费用省?请说明理由。
拓展延伸
解:(1) Y1=8x,Y2=4x+120
(2)由图象可知,当x=30 时,两家一样,
当X>30时,照相馆省钱,
当X<30时,学校自己省钱.
30
y
x
0
Y=4x+120
Y=8x
一)回顾与思考
1.如果y=kx+b(k,b是常数,k≠0),那么y叫做x的_______。
2.一次函数y=kx+b(k≠0) 的图象是________
3.一次函数y=kx+b(k≠0),当y>0时,则kx+b__0;当y<0时,则kx+b__0.
4.一次函数y=2x-6,当x___时,y>0
5.已知一次函数y1=-x-4,y2=3x+5,当x___时,y1< y2
6.一次函数y=kx+b(k≠0)与坐标轴交点坐标的求法;
练一练:
如图:当x——————一次函数y=x-2的值为0 ,
引入
x=2是一元一次方程———————的解.
=2
x-2=0
3
2
x
-2
y
0
Y=x-2
4
当x=3时,函数y=x-2的值是-------
1
当x=4,函数y=x-2的值是--------
2
思考:当x为何值 时,
函数Y=x-2对应
的值大于0 ?
上节课我们用函数观点,从数和形两个角度
学习了一元一次方程求解问题。
思考:
(1)问题1与问题2有什么关系?
两个问题实际上是同一个问题,虽然结果一样,
但是表达的方式不同。因为问题1是直接求不等式2x-4 >0的解集,解得X>2,是从不等式角度进行求解。而问题2是考虑当函数 y=2x-4的函数值大于0时,自变量X的取值,是通过列不等式2x-4 > 0求解,解得X>2,是从函数的角度进行求解。
问题2:
自变量为何值时,函数y=2x-4的值大于0?
问题1:解不等式2x-4>0
探究:
我们从函数图象来看看
画出直线y=2x-4,
-4
2
y
x
0
Y=2x-4
可以看出,当x>2时,这条
直线上的点在x轴的上方,
即这时y=2x-4>0。
所以2x-4>0的解集为x>2
试一试(根据一次函数与不等式的关系填空):
求一次函数y=3x-6的函数值
小于0的自变量的取值范围。
求不等式3x+8>0的解集。
(1) 解不等式3x-6<0,可看作
(2)“当自变量x取何值时,函数y=3x+8的值大于0”可看作
-2
x
y=3x+6
y
例 根据下列一次函数的图像,直接写出下列不等式的解集
3x+6>0
(3) –x+3 ≥0
x
y
3
y=-x+3
(2)3x+6 ≤0
X>-2
(4) –x+3<0
x≤3
X≤-2
x>3
(即y>0)
(即y≤0)
(即y<0)
(即y≥0)
练习:利用y= 的图像,直接写出:
y
2
5
x
y= x+5
X=2
X<2
X>2
X<0
(即y=0)
(即y>0)
(即y<0)
(即y>5)
一次函数与一元一次不等式的关系
求ax+b>0(或<0)(a, b
是常数,a≠0)的解集
函数y= ax+b的函数值
大于0(或小于0)时x
的取值范围
直线y= ax+b在X轴上方或
下方时自变量的取值范围
从数的角度看
从形的角度看
求ax+b>0(或<0)(a, b
是常数,a≠0)的解集
可以看出,当x<2时这条直线上的点在x轴的下方,
解法一:化简得3x-6<0,画出直线y=3x-6,
即这时y=3x-6<0,所以不等式的解集为x<2
例1.用画函数图象的方法解不等式 5x+4<2x+10
y
x
-6
2
0
Y=3x-6
尝试:
解法二:画出函数 y = 2x+10 y = 5x+4图象
从图中看出:当x <2时
直线 y = 5x +4 在 y = 2x +10的下方
即 5x+4 < 2x +10
∴ 不等式 5x+4 < 2 x +10 的解集是
x < 2
Y1=5x+4
y
x
0
Y2=2X+10
2
-2
当堂检测
完成 “当堂检测”
当堂检测
1.如图是一次函数
的图象,则关于x的方程
的解为 ;关于x的不等式
的解集为 ;
的解集为 .
关于x的不等式
当堂检测
2.若关于x的不等式
的解集为
则一次函数
当
时,图象在
时,图象在x轴______.
x轴_________;当
分析:可以画出函数草图进行解答
当堂检测
3.如右图, 一次函数
的图象
经过点 ,则关于x的不等式 的解集为________________.
分析:即求y>-2时x的取值范围
当堂检测
4、看图象说不等式
的解集
x
o
y=5x-3
2
y=3x+1
7
y
当堂检测
x>2
1.如图是一次函数
的图象,则关于x的方程
的解为 ;关于x的不等式
的解集为 ;
的解集为 .
关于x的不等式
x=2
x<2
当堂检测
下方
2.若关于x的不等式
的解集为
则一次函数
当
时,图象在
时,图象在x轴______.
x轴_________;当
上方
分析:可以画出函数草图进行解答
当堂检测
3.如右图, 一次函数
的图象
经过点 ,则关于x的不等式 的解集为________________.
x<-2
分析:即求y>-2时x的取值范围
当堂检测
4、看图象解不等式
x
o
y=5x-3
2
y=3x+1
7
y
从图中看出,当x>2时,直线y=5x-3上的点在直线y=3x+1上相应点的上方,即5x-3>3x+1,所以不等式的解集为x>2。
1.这节课我们学到了哪些知识?
2.我们是用哪些方法获得这些知识的?
3.你觉得还有什么问题需要继续讨论吗?
回顾 反思
求一元一次不等式的解,可以看成某一个一次函数当自变量取何值时,函数的值大于零或等于零。
2、如图,直线L1, L2交于一点P,若y1 ≥y2 ,则( )
x ≥ 3
x ≤3
2 ≤ x ≤ 3
x ≤ 4
1、已知函数Y=3X+8,当X————————,函数
的值等于0。当X————————,函数的值大于0。当X———————— ,函数的值不大于2。
=
≤- 2
>
B
做一做
3.利用函数图象解不等式:3x-4<x+2(用两种方法)
解法1:化简不等式得2x-6<0,画出函数y=2x-6的图象。
当x<3时y=2x-6<0,所以不等式的解集为x<3。
解法2:画出函数y=3x-4和函数y=x+2的图象,交点横坐标为3。
当x<3时,对于同一个x,直线y=3x-4上的点在直线y=x+2上相应点的下方,这表示3x-4<x+2,所以不等式的解集为x< 3。
y
x
0
-6
3
Y=2x-6
3
y
x
0
y=x+2
y=3x-4
1、某单位准备和一个体车主或一国营出租车公司中的一家签订月租车合同,设汽车每月行驶x 千米,个体车主收费y1元,国营出租车公司收费为y2元,观察下列图象可知(如图1-5-2),当x________时,选用个体车较合算.
课后思考
我们学校做一批校徽,需要拍照,若到照相馆拍,每张需要8元;若学校自己拍,除买摄象机,需120元,每张还需成本4元,设需要拍X张,到照相馆拍需要Y1 元,学校自己拍需要Y2元。
1.求Y1和Y2与X的函数关系式
2.问拍这批照片到照相馆拍,费用省还是由学校自己拍费用省?请说明理由。
拓展延伸
解:(1) Y1=8x,Y2=4x+120
(2)由图象可知,当x=30 时,两家一样,
当X>30时,照相馆省钱,
当X<30时,学校自己省钱.
30
y
x
0
Y=4x+120
Y=8x
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
