北师大版八年级下册第六章第一二节复习课件(共24张PPT)
文档属性
| 名称 | 北师大版八年级下册第六章第一二节复习课件(共24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 20:59:49 | ||
图片预览




文档简介
第六章第一节、第二节
综合复习及检测
八年级数学下册
授课:徐老师
2020年4月25日
第一节平行四边形的性质 复习及检测
两组对边都不平行.
一组对边平行,
一组对边不平行.
两组对边分别平行.
四边形.
平行四边形
两组对边分别平行的四边形叫做平行四边形。
观察图形,说出下列图形边的位置有什么特征?
知识点1:
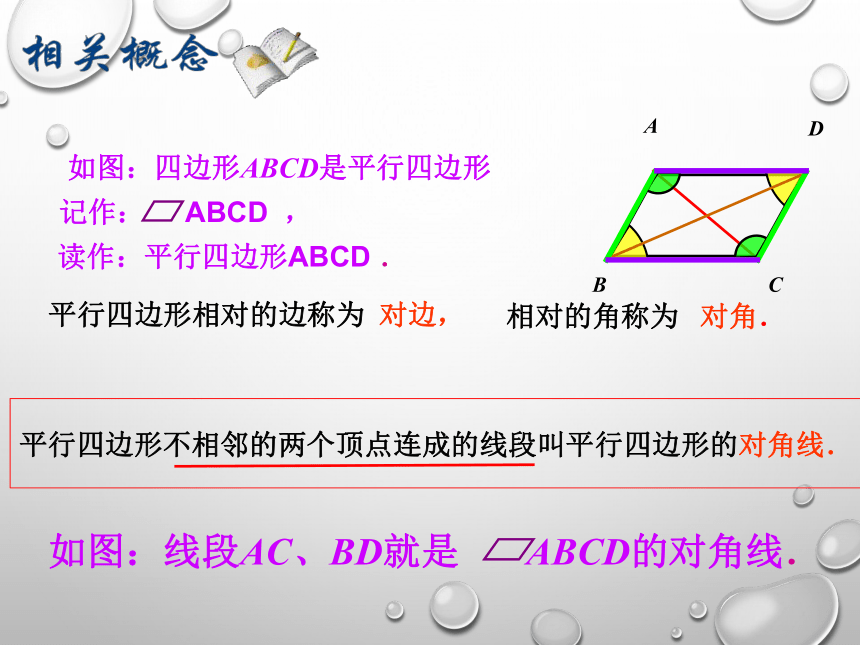
平行四边形相对的边称为 对边,
如图:线段AC、BD就是 ABCD的对角线.
A
D
C
B
平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
记作: ABCD ,
相对的角称为 对角.
如图:四边形ABCD是平行四边形
读作:平行四边形ABCD .
A
B
D
C
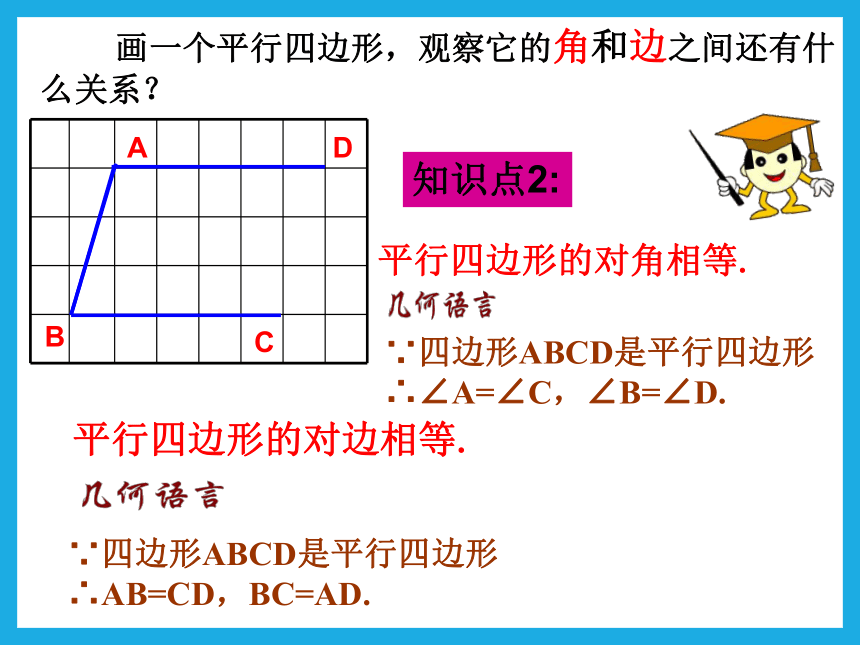
画一个平行四边形,观察它的角和边之间还有什么关系?
平行四边形的对角相等.
∵四边形ABCD是平行四边形∴AB=CD,BC=AD.
平行四边形的对边相等.
知识点2:
∵四边形ABCD是平行四边形∴∠A=∠C,∠B=∠D.
C
A
B
D
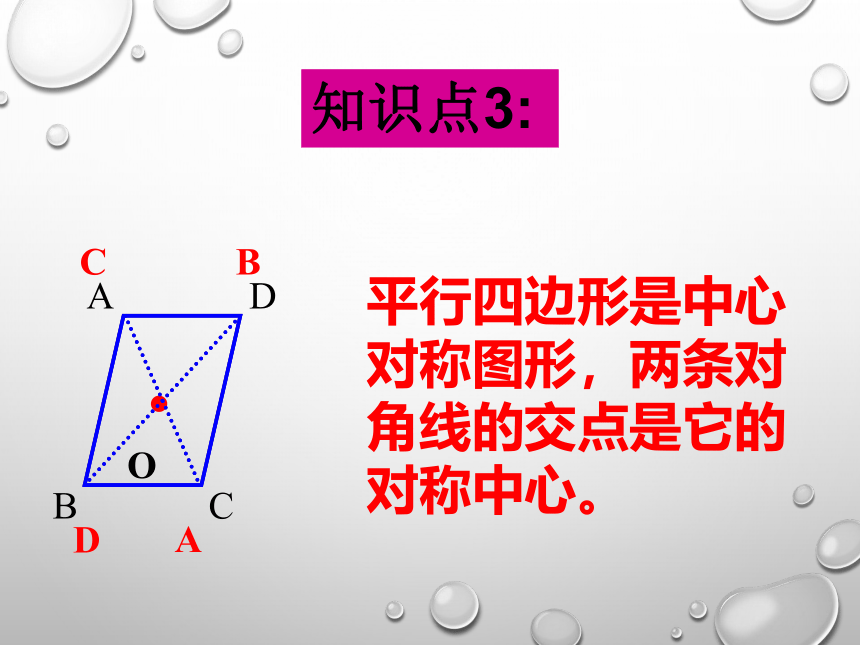
平行四边形是中心对称图形,两条对角线的交点是它的对称中心。
O
A
B
C
D
知识点3:
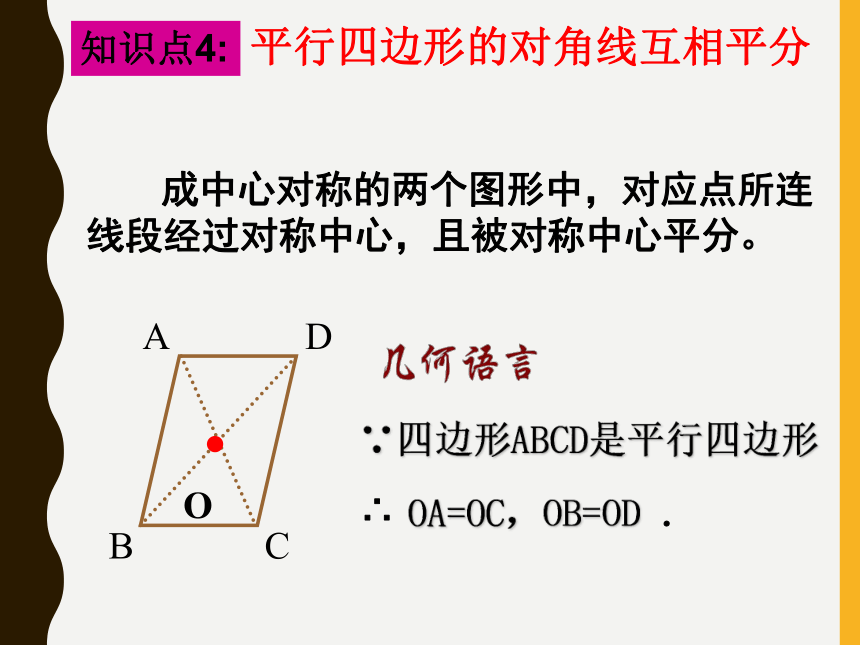
知识点4:
平行四边形的对角线互相平分
成中心对称的两个图形中,对应点所连线段经过对称中心,且被对称中心平分。
O
A
B
C
D
∵四边形ABCD是平行四边形
OA=OC,
OB=OD .
∴
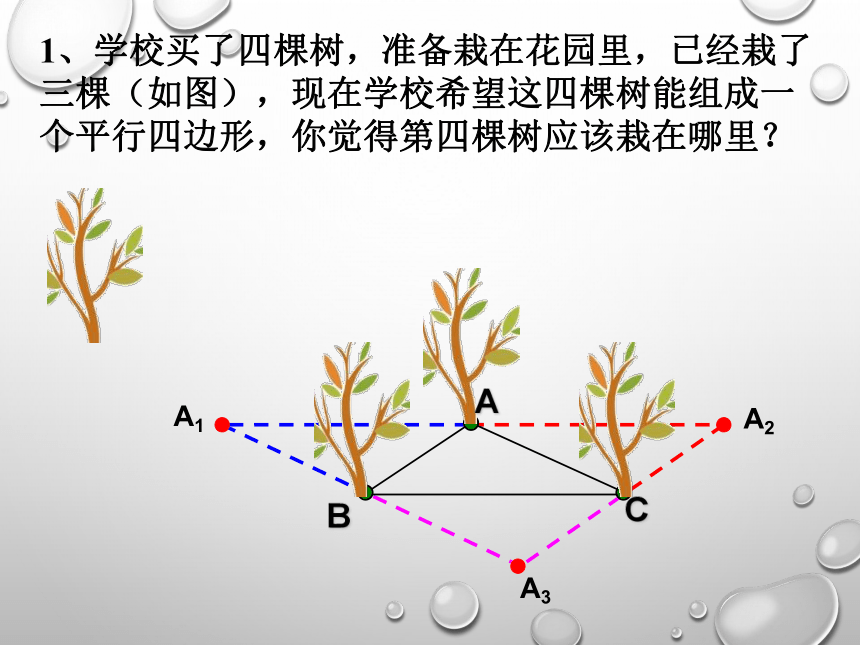
1、学校买了四棵树,准备栽在花园里,已经栽了三棵(如图),现在学校希望这四棵树能组成一个平行四边形,你觉得第四棵树应该栽在哪里?
A1
A3
A2
A
B
C
A
B
C
D
2、已知: ABCD的周长等于20 cm,AC=7 cm,求△ABC的周长.
解:
∵四边形ABCD是平行四边形(已知)
∴ AB=CD,BC=AD(平行四边形的对边相等)
即AB+BC= C ABCD =10cm,
又∵ AC=7 cm(已知)
∴ C△ ABC=AB+BC+AC=10+7=17(cm).
3、如图: 在 ABCD中,∠A+∠C=200°
则:∠A= ,∠B= .
A
D
B
C
100 °
80 °
解:
∴∠B= 180 °-∠A= 180?- 100°=80°
又∵AD∥BC(平行四边形的对边平行)
∵四边形ABCD是平行四边形
∴∠A=∠C=100 ° (平行四边形的对角相等)
且∠A+∠C=200°
4、在平行四边形ABCD中,若AE平分∠DAB,AB=5cm,AD=9cm,则EC=
C
4cm
A
B
D
E
9cm
1
2
5cm
9cm
3
5、若平行四边形的一边长为5,则它的两条对角线长可以是( )
A. 12和2 B. 3和4
C. 4和6 D. 4和8
O
D
B
A
C
D
6、如图,在平面直角坐标系中, OBCD的顶点 O﹑B﹑D的坐标如图所示,则顶点C的
坐标为( )
x
Y
C
O (0,0)
B(5,0)
D(2,3)
A. (3,7) B. (5,3)
C. (7,3) D. (8,2)
C
第二节平行四边形的判定 复习及检测
从边来判定
1、两组对边分别平行的四边形是平行四边形.
2、两组对边分别相等的四边形是平行四边形.
3、一组对边平行且相等的四边形是平行四边形.
从角来判定
4、两组对角分别相等的四边形是平行四边形.
从对角线来判定
5、两条对角线互相平分的四边形是平行四边形.
平行四边形的判定方法
l
1
l
2
E
F
C
D
A
B
∟
∟
∟
如图,l1 // l2 ,点A、C、E在l1上,线段AB、CD、EF都垂直与l2 ,垂足分别为B、D、F,则AB、CD、EF的长短相等吗?为什么?
一条直线上的任一点到另一条直线的距离,叫做这两条平行线间的距离.
平行线间的距离处处相等.
它与点与点的距离、点到直线的距离的联系与区别.
如图,l1 // l2 , 线段AB//CD//EF, 且点A、C、E在l1上,B、D、F在l2上,则AB、CD、EF的长短相等吗?为什么?
l
1
l
2
E
F
C
D
A
B
夹在两平行线间的平行线段相等.
1、如图,在平行四边形ABCD的一组对边AD、BC上截取EF=MN,连接EM、FN,EM和FN有怎样的关系?为什么?
A
B
C
D
E
F
M
N
开心一练:
2、根据下列条件,不能判定一个四边形为平行四边形的是( )
(A)两组对边分别相等.
(B)两条对角线互相平分.
(C)两条对角线相等.
(D)两组对边分别平行.
C
3、请你识别下列四边形哪些是平行四边形?请说明理由?
A
D
C
B
110°
70°
110°
⑴
⑷
⑶
A
B
C
D
120°
60°
5㎝
5㎝
A
B
C
D
O
5㎝
5㎝
4㎝
4㎝
B
A
D
C
4.8㎝
4.8㎝
⑵
7.6㎝
7.6㎝
4、已知:E、F是平行四边形ABCD对角线AC上的两点,
并且AE=CF .
求证:四边形BFDE是平行四边形.
D
O
A
B
C
E
F
证明:作对角线BD,交AC于点O
∵四边形ABCD是平行四边形,
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形.
5、如图,在□ABCD中,
AE⊥BC于E,AF⊥CD于F,
∠ADC=60°,BE=2,
CF=1 .求△DEC的面积.
解:在 ABCD中,∠ADC=∠B,AB=CD,AD=BC.
在Rt△ABE中,∠B=60°,?∠BAE=30°.
∴AB=2BE=4,AE= ??????.
∴DF=CD-CF=3
在Rt△ADF中,AD=2DF=6.
∴CE=6-2=4.
故S△DEC= ? CE·AE= ??????.
1、 通过本节课的学习,你有收获吗?
2、 平行四边形的性质共有哪些?
(四个知识点)
3、平行四边形的判定方法有哪些?
(5个定理)
1、熟练准确识记平行四边形的性质定理。
2、熟练准确识记平行四边形的判定定理。
同学们再见
综合复习及检测
八年级数学下册
授课:徐老师
2020年4月25日
第一节平行四边形的性质 复习及检测
两组对边都不平行.
一组对边平行,
一组对边不平行.
两组对边分别平行.
四边形.
平行四边形
两组对边分别平行的四边形叫做平行四边形。
观察图形,说出下列图形边的位置有什么特征?
知识点1:
平行四边形相对的边称为 对边,
如图:线段AC、BD就是 ABCD的对角线.
A
D
C
B
平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
记作: ABCD ,
相对的角称为 对角.
如图:四边形ABCD是平行四边形
读作:平行四边形ABCD .
A
B
D
C
画一个平行四边形,观察它的角和边之间还有什么关系?
平行四边形的对角相等.
∵四边形ABCD是平行四边形∴AB=CD,BC=AD.
平行四边形的对边相等.
知识点2:
∵四边形ABCD是平行四边形∴∠A=∠C,∠B=∠D.
C
A
B
D
平行四边形是中心对称图形,两条对角线的交点是它的对称中心。
O
A
B
C
D
知识点3:
知识点4:
平行四边形的对角线互相平分
成中心对称的两个图形中,对应点所连线段经过对称中心,且被对称中心平分。
O
A
B
C
D
∵四边形ABCD是平行四边形
OA=OC,
OB=OD .
∴
1、学校买了四棵树,准备栽在花园里,已经栽了三棵(如图),现在学校希望这四棵树能组成一个平行四边形,你觉得第四棵树应该栽在哪里?
A1
A3
A2
A
B
C
A
B
C
D
2、已知: ABCD的周长等于20 cm,AC=7 cm,求△ABC的周长.
解:
∵四边形ABCD是平行四边形(已知)
∴ AB=CD,BC=AD(平行四边形的对边相等)
即AB+BC= C ABCD =10cm,
又∵ AC=7 cm(已知)
∴ C△ ABC=AB+BC+AC=10+7=17(cm).
3、如图: 在 ABCD中,∠A+∠C=200°
则:∠A= ,∠B= .
A
D
B
C
100 °
80 °
解:
∴∠B= 180 °-∠A= 180?- 100°=80°
又∵AD∥BC(平行四边形的对边平行)
∵四边形ABCD是平行四边形
∴∠A=∠C=100 ° (平行四边形的对角相等)
且∠A+∠C=200°
4、在平行四边形ABCD中,若AE平分∠DAB,AB=5cm,AD=9cm,则EC=
C
4cm
A
B
D
E
9cm
1
2
5cm
9cm
3
5、若平行四边形的一边长为5,则它的两条对角线长可以是( )
A. 12和2 B. 3和4
C. 4和6 D. 4和8
O
D
B
A
C
D
6、如图,在平面直角坐标系中, OBCD的顶点 O﹑B﹑D的坐标如图所示,则顶点C的
坐标为( )
x
Y
C
O (0,0)
B(5,0)
D(2,3)
A. (3,7) B. (5,3)
C. (7,3) D. (8,2)
C
第二节平行四边形的判定 复习及检测
从边来判定
1、两组对边分别平行的四边形是平行四边形.
2、两组对边分别相等的四边形是平行四边形.
3、一组对边平行且相等的四边形是平行四边形.
从角来判定
4、两组对角分别相等的四边形是平行四边形.
从对角线来判定
5、两条对角线互相平分的四边形是平行四边形.
平行四边形的判定方法
l
1
l
2
E
F
C
D
A
B
∟
∟
∟
如图,l1 // l2 ,点A、C、E在l1上,线段AB、CD、EF都垂直与l2 ,垂足分别为B、D、F,则AB、CD、EF的长短相等吗?为什么?
一条直线上的任一点到另一条直线的距离,叫做这两条平行线间的距离.
平行线间的距离处处相等.
它与点与点的距离、点到直线的距离的联系与区别.
如图,l1 // l2 , 线段AB//CD//EF, 且点A、C、E在l1上,B、D、F在l2上,则AB、CD、EF的长短相等吗?为什么?
l
1
l
2
E
F
C
D
A
B
夹在两平行线间的平行线段相等.
1、如图,在平行四边形ABCD的一组对边AD、BC上截取EF=MN,连接EM、FN,EM和FN有怎样的关系?为什么?
A
B
C
D
E
F
M
N
开心一练:
2、根据下列条件,不能判定一个四边形为平行四边形的是( )
(A)两组对边分别相等.
(B)两条对角线互相平分.
(C)两条对角线相等.
(D)两组对边分别平行.
C
3、请你识别下列四边形哪些是平行四边形?请说明理由?
A
D
C
B
110°
70°
110°
⑴
⑷
⑶
A
B
C
D
120°
60°
5㎝
5㎝
A
B
C
D
O
5㎝
5㎝
4㎝
4㎝
B
A
D
C
4.8㎝
4.8㎝
⑵
7.6㎝
7.6㎝
4、已知:E、F是平行四边形ABCD对角线AC上的两点,
并且AE=CF .
求证:四边形BFDE是平行四边形.
D
O
A
B
C
E
F
证明:作对角线BD,交AC于点O
∵四边形ABCD是平行四边形,
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形.
5、如图,在□ABCD中,
AE⊥BC于E,AF⊥CD于F,
∠ADC=60°,BE=2,
CF=1 .求△DEC的面积.
解:在 ABCD中,∠ADC=∠B,AB=CD,AD=BC.
在Rt△ABE中,∠B=60°,?∠BAE=30°.
∴AB=2BE=4,AE= ??????.
∴DF=CD-CF=3
在Rt△ADF中,AD=2DF=6.
∴CE=6-2=4.
故S△DEC= ? CE·AE= ??????.
1、 通过本节课的学习,你有收获吗?
2、 平行四边形的性质共有哪些?
(四个知识点)
3、平行四边形的判定方法有哪些?
(5个定理)
1、熟练准确识记平行四边形的性质定理。
2、熟练准确识记平行四边形的判定定理。
同学们再见
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
