北师大版八年级下册数学 3.3 中心对称 课件 (共22张PPT)
文档属性
| 名称 | 北师大版八年级下册数学 3.3 中心对称 课件 (共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 22:04:01 | ||
图片预览



文档简介
3.3 中心对称
第三章 图形的平移与旋转
【学习目标】
1.了解中心对称、中心对称图形的概念,探索它的基本性质.
2.认识和欣赏自然界和现实生活中的中心对称图形.
3.熟练地画出已知图形关于某一点成中心对称的图形.
【重点】识别中心对称图形和成中心对称的两个图形的基本特征;熟练地画出已知图形关于某一点成中心对称的图形.
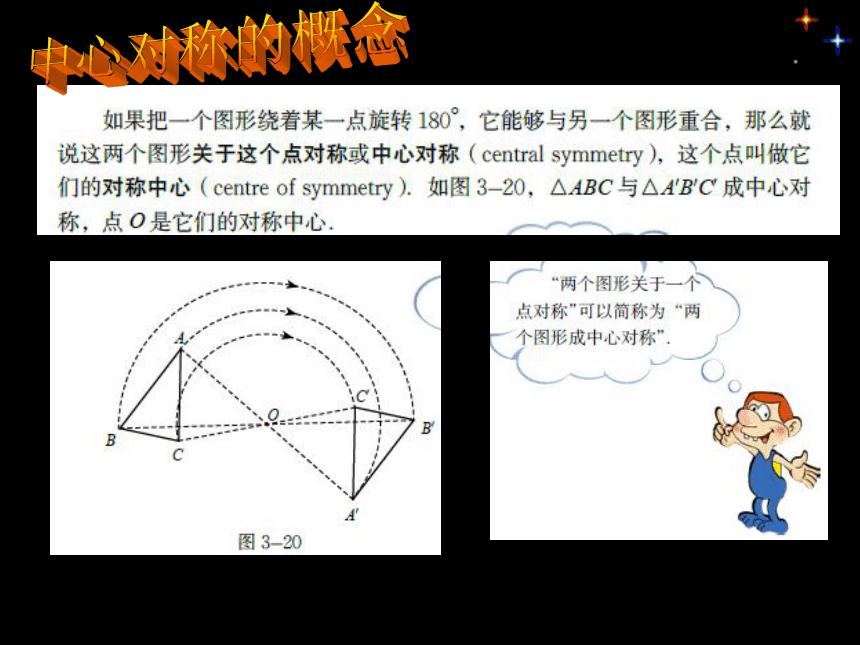
观察发现1
中心对称的概念
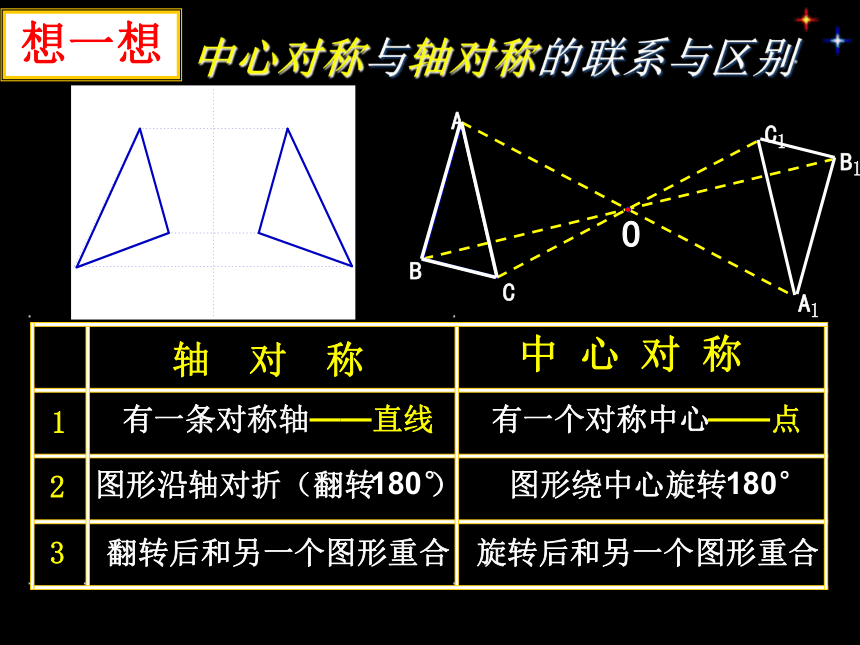
轴 对 称
中 心 对 称
1
有一条对称轴
——
直线
有一个对称中心
——
点
2
图形沿轴对折(翻转
180°
)
图形绕中心旋转
180°
3
翻转后和另一个图形重合
旋转后和另一个图形重合
A
B
C
C
1
A
1
B
1
O
想一想
中心对称与轴对称的联系与区别
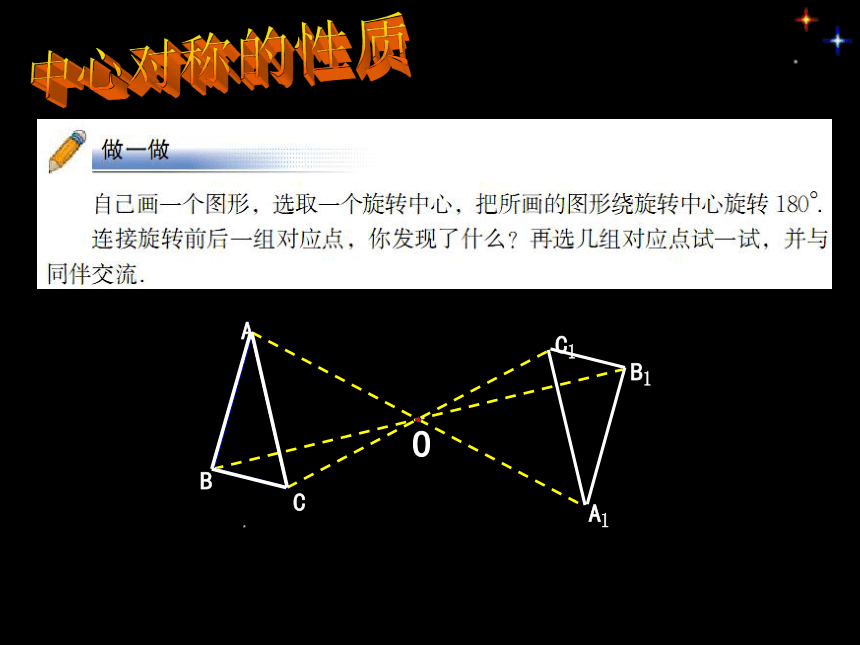
中心对称的性质
A
B
C
C
1
A
1
B
1
O
A
B
C
C
1
A
1
B
1
O
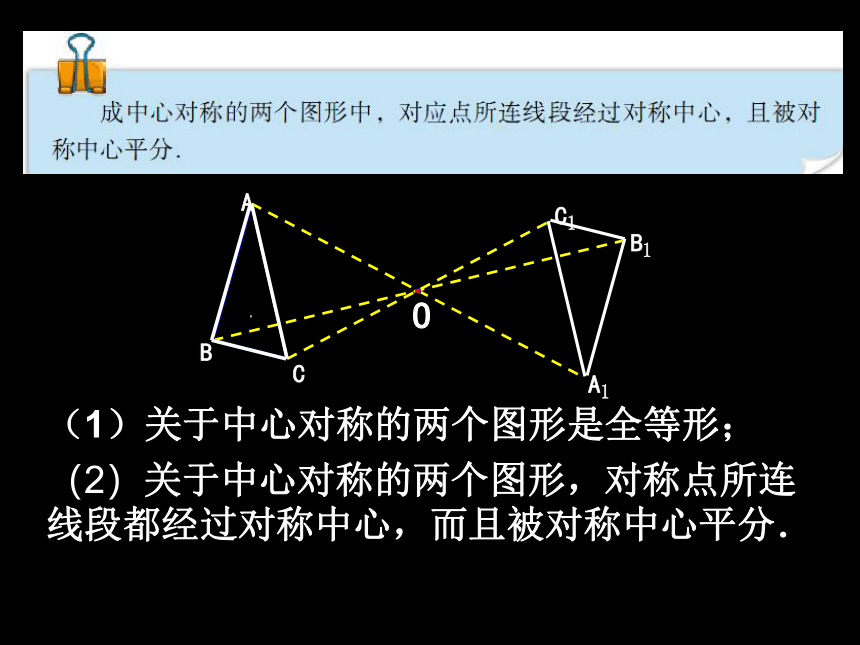
(2)关于中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心平分.
(1)关于中心对称的两个图形是全等形;
A
O
A′
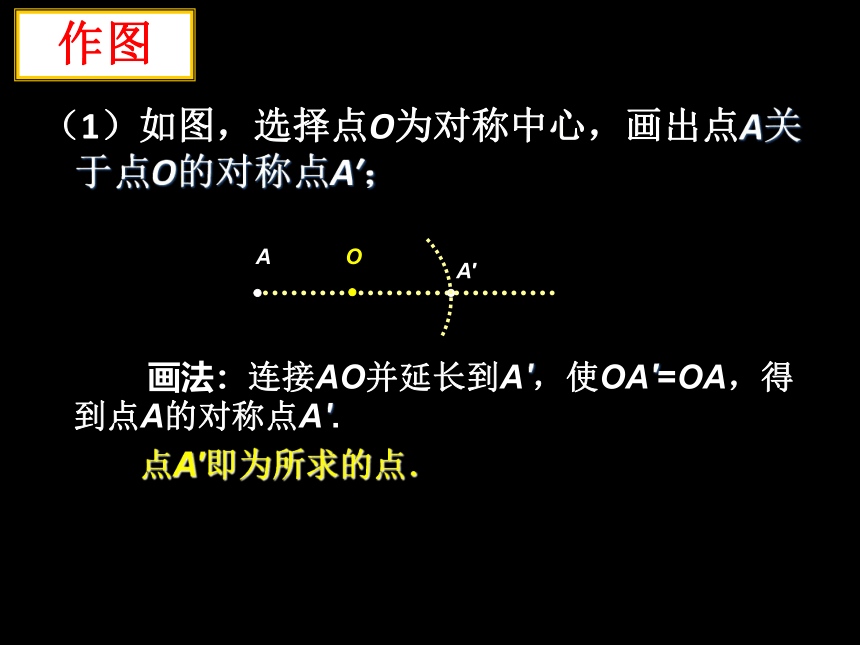
(1)如图,选择点O为对称中心,画出点A关于点O的对称点A′;
点A′即为所求的点.
画法:连接AO并延长到A′,使OA′=OA,得到点A的对称点A′.
作图
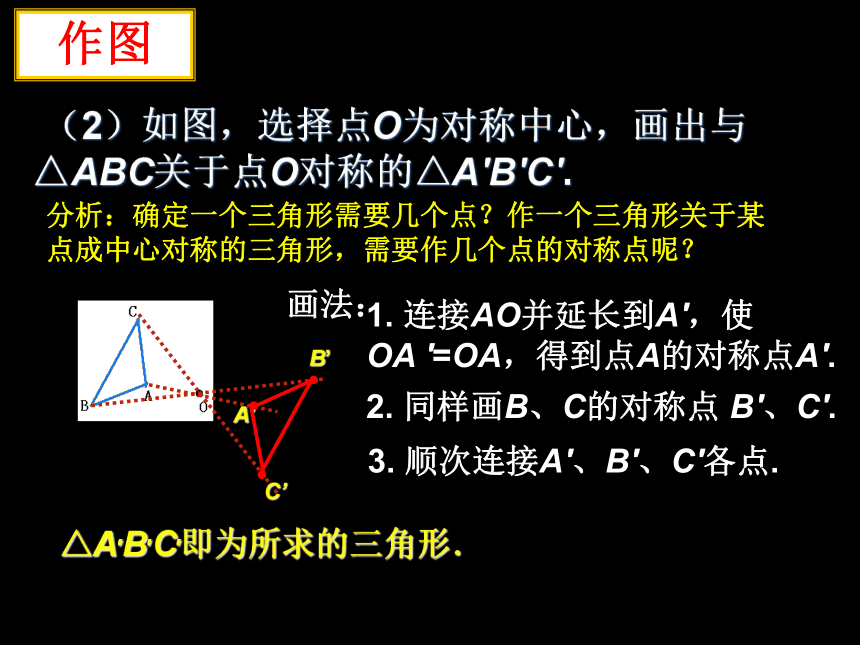
(2)如图,选择点O为对称中心,画出与△ABC关于点O对称的△A′B′C′.
A’
C’
B’
△A′B′C′即为所求的三角形.
1. 连接AO并延长到A′,使
OA ′=OA,得到点A的对称点A′.
2. 同样画B、C的对称点 B′、C′.
3. 顺次连接A′、B′、C′各点.
画法:
分析:确定一个三角形需要几个点?作一个三角形关于某点成中心对称的三角形,需要作几个点的对称点呢?
作图
举例
D
A
B
C
O
.
画一个与已知四边形ABCD成中心对称的图形.
(1)以顶点A为对称中心;
(2)以BC边的中点为对称中心.
D
A
B
C
E
F
G
M
N
巩固练习
(1)
(2)
(3)
(4)
下列图形旋转多少度与自身重合?
A
B
O
(5)
至少旋转多少度与自身重合?
观察发现2
中心对称图形的概念
中心对称与中心对称图形的联系与区别
区别:
中心对称指两个全等图形的相互位置关系,中心对称图形指一个图形本身成中心对称.
联系:
如果将中心对称图形的两个图形看成一个整体,则它们是中心对称图形.
如果将中心对称图形对称的部分看成两个图形,则它们成中心对称.
想一想
我们平时见过的几何图形中,有哪些是中心对称图形?并指出对称中心.
怎样的多边形是中心对称图形?
偶数边的正多边形
想一想
对
图 称
形 性
轴对称图形
中心对称图形
图形
对称轴条数
图形
对称中心
线段
角
等腰三角形
等边三角形
平行四边形
矩形
菱形
正方形
等腰梯形
常见的轴对称图形与中心对称图形
2条
1条
1条
3条
2条
2条
4条
1条
中点
对角线交点
对角线交点
对角线交点
对角线交点
无
无
无
无
无
1.下列图形中既是轴对称图形又是中心对称图形的是 .
①角 ②正三角形 ③线段 ④ 平行四边形
③
巩固练习
填空题:
2.下列多边形中,是中心对称图形而不是轴对称图形的是 .
① 平行四边形 ② 矩形 ③ 菱形 ④ 正方形
①
3.下列多边形中,是轴对称图形而不是中心对称图形的是 .
① 平行四边形 ② 矩形 ③ 菱形 ④ 等腰梯形
④
注意:
等边三角形不是中心对称图形!
是轴对称图形
O
A
B
C
D
O
注意:
平行四边形不是轴对称图形!
是中心对称图形
谈谈收获
对自己说,你有什么收获!
对教师说,你有什么疑惑!
对同学说,你有什么提示!
第三章 图形的平移与旋转
【学习目标】
1.了解中心对称、中心对称图形的概念,探索它的基本性质.
2.认识和欣赏自然界和现实生活中的中心对称图形.
3.熟练地画出已知图形关于某一点成中心对称的图形.
【重点】识别中心对称图形和成中心对称的两个图形的基本特征;熟练地画出已知图形关于某一点成中心对称的图形.
观察发现1
中心对称的概念
轴 对 称
中 心 对 称
1
有一条对称轴
——
直线
有一个对称中心
——
点
2
图形沿轴对折(翻转
180°
)
图形绕中心旋转
180°
3
翻转后和另一个图形重合
旋转后和另一个图形重合
A
B
C
C
1
A
1
B
1
O
想一想
中心对称与轴对称的联系与区别
中心对称的性质
A
B
C
C
1
A
1
B
1
O
A
B
C
C
1
A
1
B
1
O
(2)关于中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心平分.
(1)关于中心对称的两个图形是全等形;
A
O
A′
(1)如图,选择点O为对称中心,画出点A关于点O的对称点A′;
点A′即为所求的点.
画法:连接AO并延长到A′,使OA′=OA,得到点A的对称点A′.
作图
(2)如图,选择点O为对称中心,画出与△ABC关于点O对称的△A′B′C′.
A’
C’
B’
△A′B′C′即为所求的三角形.
1. 连接AO并延长到A′,使
OA ′=OA,得到点A的对称点A′.
2. 同样画B、C的对称点 B′、C′.
3. 顺次连接A′、B′、C′各点.
画法:
分析:确定一个三角形需要几个点?作一个三角形关于某点成中心对称的三角形,需要作几个点的对称点呢?
作图
举例
D
A
B
C
O
.
画一个与已知四边形ABCD成中心对称的图形.
(1)以顶点A为对称中心;
(2)以BC边的中点为对称中心.
D
A
B
C
E
F
G
M
N
巩固练习
(1)
(2)
(3)
(4)
下列图形旋转多少度与自身重合?
A
B
O
(5)
至少旋转多少度与自身重合?
观察发现2
中心对称图形的概念
中心对称与中心对称图形的联系与区别
区别:
中心对称指两个全等图形的相互位置关系,中心对称图形指一个图形本身成中心对称.
联系:
如果将中心对称图形的两个图形看成一个整体,则它们是中心对称图形.
如果将中心对称图形对称的部分看成两个图形,则它们成中心对称.
想一想
我们平时见过的几何图形中,有哪些是中心对称图形?并指出对称中心.
怎样的多边形是中心对称图形?
偶数边的正多边形
想一想
对
图 称
形 性
轴对称图形
中心对称图形
图形
对称轴条数
图形
对称中心
线段
角
等腰三角形
等边三角形
平行四边形
矩形
菱形
正方形
等腰梯形
常见的轴对称图形与中心对称图形
2条
1条
1条
3条
2条
2条
4条
1条
中点
对角线交点
对角线交点
对角线交点
对角线交点
无
无
无
无
无
1.下列图形中既是轴对称图形又是中心对称图形的是 .
①角 ②正三角形 ③线段 ④ 平行四边形
③
巩固练习
填空题:
2.下列多边形中,是中心对称图形而不是轴对称图形的是 .
① 平行四边形 ② 矩形 ③ 菱形 ④ 正方形
①
3.下列多边形中,是轴对称图形而不是中心对称图形的是 .
① 平行四边形 ② 矩形 ③ 菱形 ④ 等腰梯形
④
注意:
等边三角形不是中心对称图形!
是轴对称图形
O
A
B
C
D
O
注意:
平行四边形不是轴对称图形!
是中心对称图形
谈谈收获
对自己说,你有什么收获!
对教师说,你有什么疑惑!
对同学说,你有什么提示!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
