北师大版八年级下册数学 4.3公式法(2)用完全平方公式因式分解课件 (共26张PPT)
文档属性
| 名称 | 北师大版八年级下册数学 4.3公式法(2)用完全平方公式因式分解课件 (共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 21:06:10 | ||
图片预览








文档简介
4.3
公式法(2)
——用完全平方公式因式分解
提取公因式法:ma+mb+mc=m(a+b+c)
运用公式法: ① a2-b2=(a+b)(a-b)
练习
把下列各式分解因式
① ② x4-16
解:原式=ax2(x2-1)
=ax2(x+1)(x-1)
解:原式=(x2+4)(x2-4)
=(x2 +4)(x+2)(x-2)
课前复习:1、因式分解学了哪些方法?
(一提二套。)
(因式分解要彻底。)
课前复习:
2.除了平方差公式外,还学过了哪些公式?
现在我们把完全平方公式反过来,可得:
两个数的平方和,加上 这两个数的积的两倍,等于这两数和 的平方.
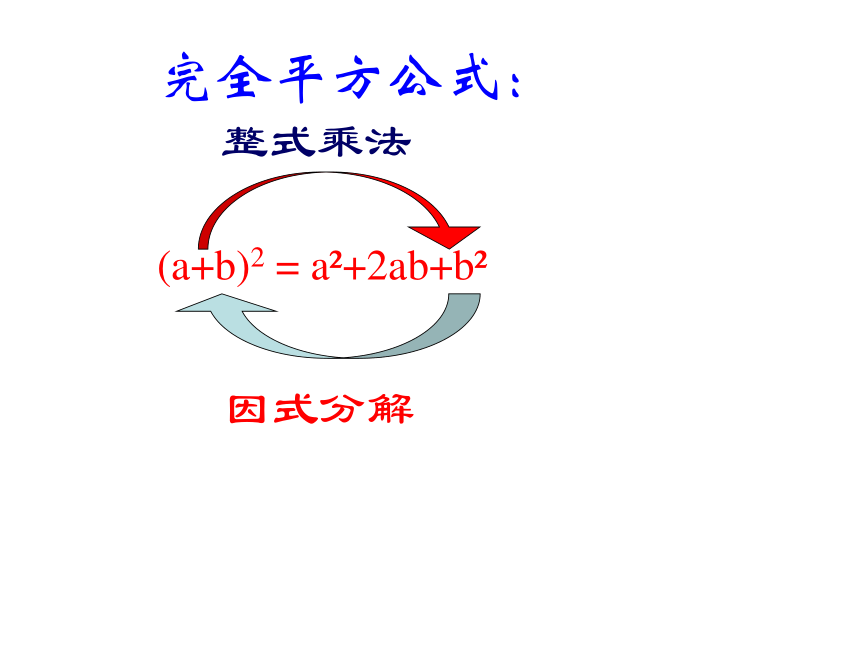
完全平方公式:
(或减去)
(或者差)
完全平方公式:
(a+b)2 = a?+2ab+b?
整式乘法
因式分解
两个数的平方和,加上(或减去)这两个数的积的两倍,等于这两数和(或者差)的平方.
形如 的多项式称为完全平方式.
平方差公式法和完全平方公式法统称公式法。
平方差公式法:适用于平方差形式的多项式
完全平方公式法:适用于完全平方式的多项式
完全平方式的特点:
1、必须是三项式;
2、有两个同号的平方项;
3、有一个乘积项(等于平方项底数的±2倍)。
简记口诀:
首平方,尾平方,首尾两倍在中央。
1.判别下列各式是不是完全平方式.
不是
是
是
不是
练一练:
是
如何运用完全平方公式进行因式分解呢?
16x2+40x+25= ( )2+2( )( )+( )2 =( + )2
=( )2- 2( )( )+( )2 =( - )2
4x
4x
4x
5
5
5
n
n
n
对照公式填一填
2.判别下列各式是不是完全平方式?若是,说出
相应的 各表示什么?
是
不是
不是
是
不是
是
练一练:
3.请补上一项,使下列多项式成为完全平方式.
练一练:
(±12ab)
(±4xy)
(1)
x2+14x+49
解:
(2)
解:
例题
找到完全平方式中的“头”和“尾”,确定中间项的符号。
(3)
3ax2+6axy+3ay2
解:
(4)
例题
-x2-4y2+4xy
解:
若多项式中有公因式,应先提取公因式,然后再进一步分解因式。
2. 把下列各式分解因式:
P102随堂练习1
1、是一个二次三项式;
一、完全平方式的特点:
小结:
2、有两个“项”平方,而且有这两“项”的积的两倍或负两倍;
3、我们可以利用完全平方公式来进行因式分解。
因式分解多项式;先看有无公因式。两项三项用公式;辨明是否标准式。
二、因式分解的基本思路
因式分解顺口溜——
若要分解多项式,先看有无公因式;
看到两次两项式,就用平方差公式;
遇到两次三项式,应用完全平方式;
结果都是积整式,彻底分解多项式。
作业
P103习题4.5
(第1、2题)
3.按照完全平方公式填空:
练一练:
例1:把下列各式分解因式:
若多项式中有公因式,应先提取公因式,然后再进一步分解因式。
平方项有负先提负
做一做:分解因式课内练习T1:
例2:因式分解:
把2x+y看做
a2-2ab+b2
中的字母“a”
即设a= 2x+y ,
这种数学思想称
为换元思想
(2) a(9a-6b)+b2
(3)(a-b)2-10(a-b)+25
(4) (4x2+1)2-16x2
练习:因式分解:
(1)-a?+8a-16
提高拓展:
用简便方法计算:
挑战1:
将 再加上一项,使它成为完全平方式,你有几种方法?
一天,小明在纸上写了一个算式为 4x2 +8x+11,并对小刚说:“无论x取何值,这个代数式的值都是正值,你不信试一试?”
你知道其中的奥妙吗?
挑战2:
1、已知x2+y2+6x-4y+13=0.则xy= 。
2、多项式:
(x+y)2-2(x2-y2)+(x-y)2能用完全平方公式分解吗?
[(x+y)-(x-y)]2=(2y)2=4y2
公式法(2)
——用完全平方公式因式分解
提取公因式法:ma+mb+mc=m(a+b+c)
运用公式法: ① a2-b2=(a+b)(a-b)
练习
把下列各式分解因式
① ② x4-16
解:原式=ax2(x2-1)
=ax2(x+1)(x-1)
解:原式=(x2+4)(x2-4)
=(x2 +4)(x+2)(x-2)
课前复习:1、因式分解学了哪些方法?
(一提二套。)
(因式分解要彻底。)
课前复习:
2.除了平方差公式外,还学过了哪些公式?
现在我们把完全平方公式反过来,可得:
两个数的平方和,加上 这两个数的积的两倍,等于这两数和 的平方.
完全平方公式:
(或减去)
(或者差)
完全平方公式:
(a+b)2 = a?+2ab+b?
整式乘法
因式分解
两个数的平方和,加上(或减去)这两个数的积的两倍,等于这两数和(或者差)的平方.
形如 的多项式称为完全平方式.
平方差公式法和完全平方公式法统称公式法。
平方差公式法:适用于平方差形式的多项式
完全平方公式法:适用于完全平方式的多项式
完全平方式的特点:
1、必须是三项式;
2、有两个同号的平方项;
3、有一个乘积项(等于平方项底数的±2倍)。
简记口诀:
首平方,尾平方,首尾两倍在中央。
1.判别下列各式是不是完全平方式.
不是
是
是
不是
练一练:
是
如何运用完全平方公式进行因式分解呢?
16x2+40x+25= ( )2+2( )( )+( )2 =( + )2
=( )2- 2( )( )+( )2 =( - )2
4x
4x
4x
5
5
5
n
n
n
对照公式填一填
2.判别下列各式是不是完全平方式?若是,说出
相应的 各表示什么?
是
不是
不是
是
不是
是
练一练:
3.请补上一项,使下列多项式成为完全平方式.
练一练:
(±12ab)
(±4xy)
(1)
x2+14x+49
解:
(2)
解:
例题
找到完全平方式中的“头”和“尾”,确定中间项的符号。
(3)
3ax2+6axy+3ay2
解:
(4)
例题
-x2-4y2+4xy
解:
若多项式中有公因式,应先提取公因式,然后再进一步分解因式。
2. 把下列各式分解因式:
P102随堂练习1
1、是一个二次三项式;
一、完全平方式的特点:
小结:
2、有两个“项”平方,而且有这两“项”的积的两倍或负两倍;
3、我们可以利用完全平方公式来进行因式分解。
因式分解多项式;先看有无公因式。两项三项用公式;辨明是否标准式。
二、因式分解的基本思路
因式分解顺口溜——
若要分解多项式,先看有无公因式;
看到两次两项式,就用平方差公式;
遇到两次三项式,应用完全平方式;
结果都是积整式,彻底分解多项式。
作业
P103习题4.5
(第1、2题)
3.按照完全平方公式填空:
练一练:
例1:把下列各式分解因式:
若多项式中有公因式,应先提取公因式,然后再进一步分解因式。
平方项有负先提负
做一做:分解因式课内练习T1:
例2:因式分解:
把2x+y看做
a2-2ab+b2
中的字母“a”
即设a= 2x+y ,
这种数学思想称
为换元思想
(2) a(9a-6b)+b2
(3)(a-b)2-10(a-b)+25
(4) (4x2+1)2-16x2
练习:因式分解:
(1)-a?+8a-16
提高拓展:
用简便方法计算:
挑战1:
将 再加上一项,使它成为完全平方式,你有几种方法?
一天,小明在纸上写了一个算式为 4x2 +8x+11,并对小刚说:“无论x取何值,这个代数式的值都是正值,你不信试一试?”
你知道其中的奥妙吗?
挑战2:
1、已知x2+y2+6x-4y+13=0.则xy= 。
2、多项式:
(x+y)2-2(x2-y2)+(x-y)2能用完全平方公式分解吗?
[(x+y)-(x-y)]2=(2y)2=4y2
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
