北师大版八年级下册数学:1.4角平分线 课件(共15张PPT)
文档属性
| 名称 | 北师大版八年级下册数学:1.4角平分线 课件(共15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 729.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 22:07:08 | ||
图片预览



文档简介
第四节 角平分线 (1)
还记得角平分线上的点有什么性质吗?你是怎样得到的?
角平分线上的点到角两边的距离相等.
用心想一想
我们来证明这个命题的正确性。
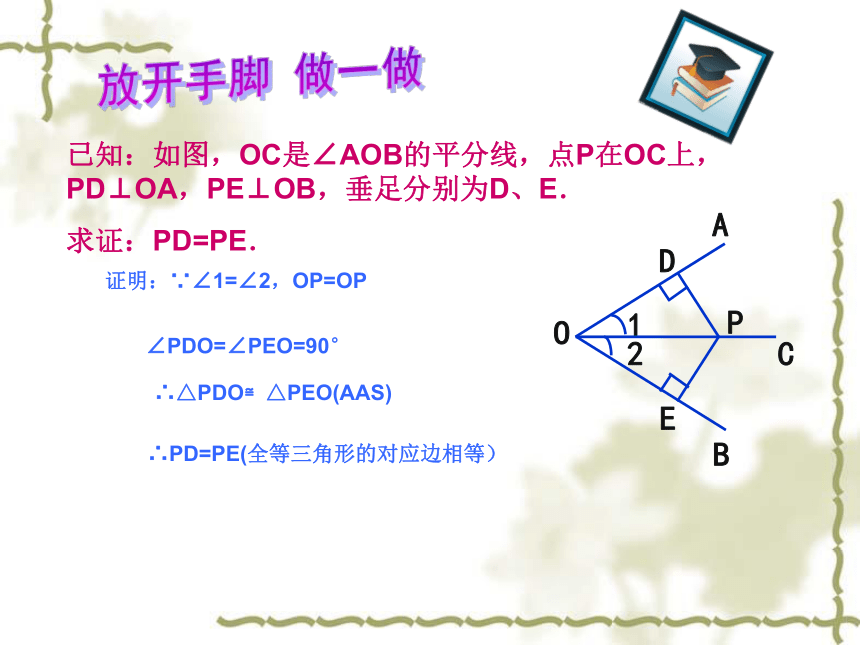
已知:如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D、E.
求证:PD=PE.
C
B
1
A
2
P
D
E
O
证明:∵∠1=∠2,OP=OP
∠PDO=∠PEO=90°
∴△PDO≌△PEO(AAS)
∴PD=PE(全等三角形的对应边相等)
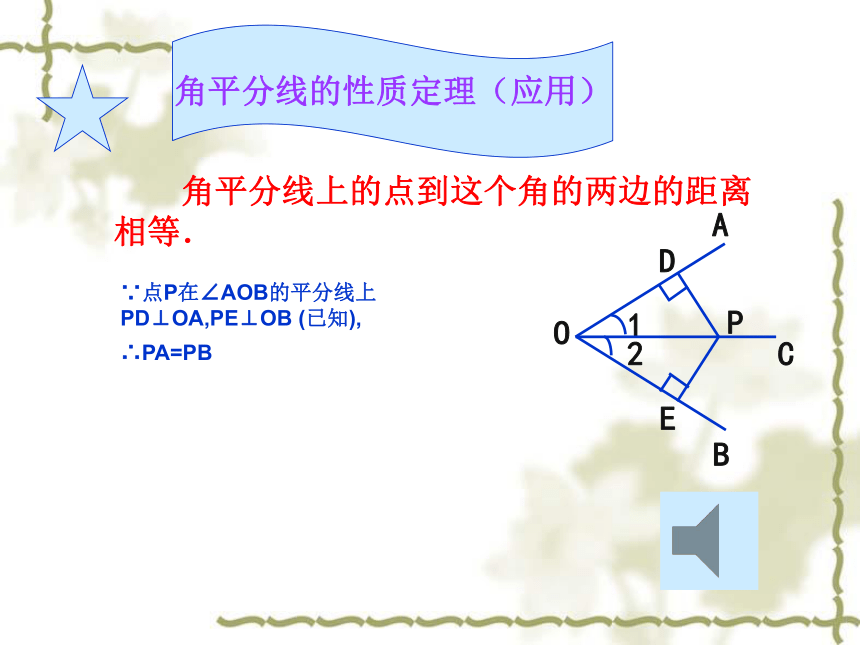
角平分线上的点到这个角的两边的距离相等.
C
B
1
A
2
P
D
E
O
∵点P在∠AOB的平分线上 PD⊥OA,PE⊥OB (已知),
角平分线的性质定理(应用)
∴PA=PB
如果有一个点到角两边的距离相等,那么这个点必在这个角的平分线上.
你能写出这个定理的逆命题吗?
用心想一想
角平分线性质定理的逆命题:在一个角的内部且到角的两边距离相等的点,在这个角的角平分线上.
这是一个真命题吗?
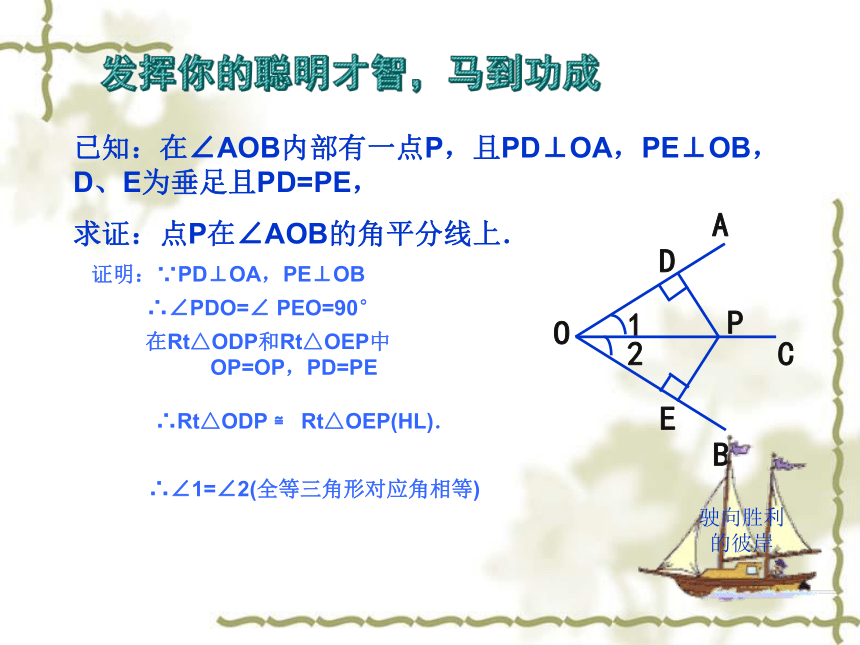
已知:在∠AOB内部有一点P,且PD⊥OA,PE⊥OB,D、E为垂足且PD=PE,
求证:点P在∠AOB的角平分线上.
C
B
1
A
2
P
D
E
O
证明:∵PD⊥OA,PE⊥OB
∴∠PDO=∠ PEO=90°
在Rt△ODP和Rt△OEP中
OP=OP,PD=PE
∴Rt△ODP ≌ Rt△OEP(HL).
∴∠1=∠2(全等三角形对应角相等)
驶向胜利的彼岸
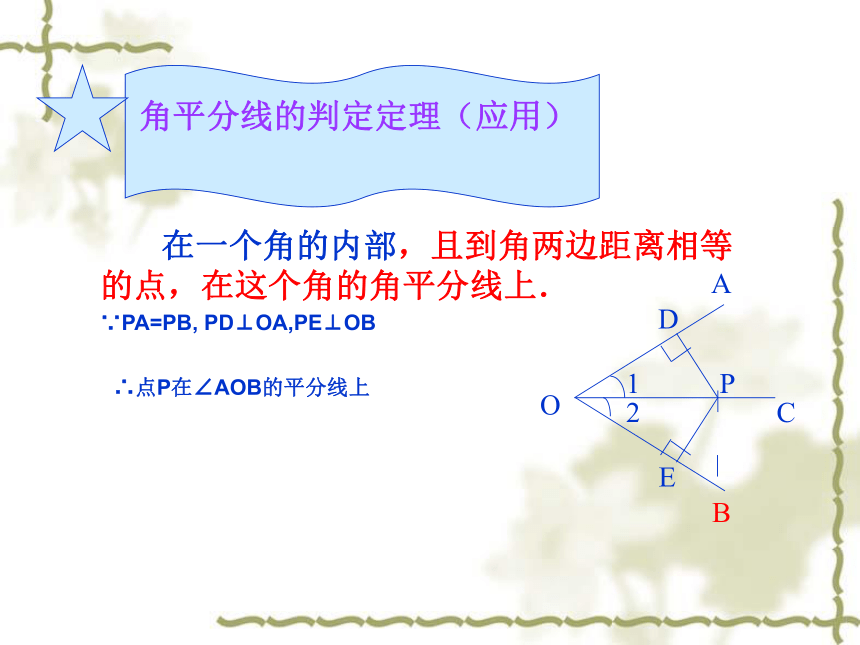
在一个角的内部,且到角两边距离相等的点,在这个角的角平分线上.
∵PA=PB, PD⊥OA,PE⊥OB
∴点P在∠AOB的平分线上
O
C
B
1
A
2
P
D
E
角平分线的判定定理(应用)
驶向胜利的彼岸
尺规作图
做一做
1
已知:∠AOB,如图.
求作:射线OC,使∠AOC=∠BOC.
作法:
用尺规作角的平分线.
1.在OA和OB上分别截取OD,OE,使OD=OE.
2.分别以点D和E为圆心,以大于DE/2长为半径作弧,两弧在 ∠AOB内交于点C..
3.作射线OC.
老师提示:
作角平分线是最基本的尺规作图,这种方法要确实掌握.
A
B
O
C
则射线OC就是∠AOB的平分线.
D
E
例题讲析
例1 如图,在△ABC中,∠BAC=60°,点D在BC上,AD=10,DE⊥AB,DF⊥AC,垂足分别为E,F,且DE=DF,求DE的长.
(在一个角的内部,到角的两边距离相等的点在这个角的平分线上).
又∵ ∠BAC=60°
∴ ∠BAD=30°.
在Rt △ADE中, ∠AED=90°,AD=10,
∴DE= AD= ×10=5
(在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半).
B
F
E
D
C
A
解: ∵DE ⊥ AB,DF ⊥ AC,垂足分别为E,F,且DE=DF,
∴AD平分∠BAC
挑战自我
随堂练习
1
驶向胜利的彼岸
如图,AD,AE分别是△ABC中∠A的内角平分线外角平分线,它们有什么关系?
老师期望:
你能说出结论并能证明它.
E
D
A
B
C
F
2.如图,一目标在A区,到期公路,铁路距离相等,离公路与铁路的交叉处500m.在图上标出它的位置(比例尺 1:20 000).
随堂练习
2
梦想成真
A区
回味无穷
小结 拓展
角平分线的性质定理
角平分线上的点到这个角的两边的距离相等.
∵点P在∠AOB的平分线上 PD⊥OA,PE⊥OB (已知),
∴ PA=PB
C
B
1
A
2
P
D
E
O
角平分线的判定定理
在一个角的内部,且到角两边距离相等的点,在这个角的角平分线上.
∵PA=PB, PD⊥OA,PE⊥OB
∴点P在∠AOB的平分线上
用尺规作角的平分线.
如图,在
AOB
内部求作一点p,使pc=Pd,并且p点到
AOB两边的距离相等
0
C
D
B
A
知识的升华
独立
作业
P 31习题1.7 第2题.
祝你成功!
结束寄语
严格性之于数学家,犹如道德之于人.
证明的规范性在于:条理清晰,因果相应,言必有据.这是初学证明者谨记和遵循的原则.
下课了!
还记得角平分线上的点有什么性质吗?你是怎样得到的?
角平分线上的点到角两边的距离相等.
用心想一想
我们来证明这个命题的正确性。
已知:如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D、E.
求证:PD=PE.
C
B
1
A
2
P
D
E
O
证明:∵∠1=∠2,OP=OP
∠PDO=∠PEO=90°
∴△PDO≌△PEO(AAS)
∴PD=PE(全等三角形的对应边相等)
角平分线上的点到这个角的两边的距离相等.
C
B
1
A
2
P
D
E
O
∵点P在∠AOB的平分线上 PD⊥OA,PE⊥OB (已知),
角平分线的性质定理(应用)
∴PA=PB
如果有一个点到角两边的距离相等,那么这个点必在这个角的平分线上.
你能写出这个定理的逆命题吗?
用心想一想
角平分线性质定理的逆命题:在一个角的内部且到角的两边距离相等的点,在这个角的角平分线上.
这是一个真命题吗?
已知:在∠AOB内部有一点P,且PD⊥OA,PE⊥OB,D、E为垂足且PD=PE,
求证:点P在∠AOB的角平分线上.
C
B
1
A
2
P
D
E
O
证明:∵PD⊥OA,PE⊥OB
∴∠PDO=∠ PEO=90°
在Rt△ODP和Rt△OEP中
OP=OP,PD=PE
∴Rt△ODP ≌ Rt△OEP(HL).
∴∠1=∠2(全等三角形对应角相等)
驶向胜利的彼岸
在一个角的内部,且到角两边距离相等的点,在这个角的角平分线上.
∵PA=PB, PD⊥OA,PE⊥OB
∴点P在∠AOB的平分线上
O
C
B
1
A
2
P
D
E
角平分线的判定定理(应用)
驶向胜利的彼岸
尺规作图
做一做
1
已知:∠AOB,如图.
求作:射线OC,使∠AOC=∠BOC.
作法:
用尺规作角的平分线.
1.在OA和OB上分别截取OD,OE,使OD=OE.
2.分别以点D和E为圆心,以大于DE/2长为半径作弧,两弧在 ∠AOB内交于点C..
3.作射线OC.
老师提示:
作角平分线是最基本的尺规作图,这种方法要确实掌握.
A
B
O
C
则射线OC就是∠AOB的平分线.
D
E
例题讲析
例1 如图,在△ABC中,∠BAC=60°,点D在BC上,AD=10,DE⊥AB,DF⊥AC,垂足分别为E,F,且DE=DF,求DE的长.
(在一个角的内部,到角的两边距离相等的点在这个角的平分线上).
又∵ ∠BAC=60°
∴ ∠BAD=30°.
在Rt △ADE中, ∠AED=90°,AD=10,
∴DE= AD= ×10=5
(在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半).
B
F
E
D
C
A
解: ∵DE ⊥ AB,DF ⊥ AC,垂足分别为E,F,且DE=DF,
∴AD平分∠BAC
挑战自我
随堂练习
1
驶向胜利的彼岸
如图,AD,AE分别是△ABC中∠A的内角平分线外角平分线,它们有什么关系?
老师期望:
你能说出结论并能证明它.
E
D
A
B
C
F
2.如图,一目标在A区,到期公路,铁路距离相等,离公路与铁路的交叉处500m.在图上标出它的位置(比例尺 1:20 000).
随堂练习
2
梦想成真
A区
回味无穷
小结 拓展
角平分线的性质定理
角平分线上的点到这个角的两边的距离相等.
∵点P在∠AOB的平分线上 PD⊥OA,PE⊥OB (已知),
∴ PA=PB
C
B
1
A
2
P
D
E
O
角平分线的判定定理
在一个角的内部,且到角两边距离相等的点,在这个角的角平分线上.
∵PA=PB, PD⊥OA,PE⊥OB
∴点P在∠AOB的平分线上
用尺规作角的平分线.
如图,在
AOB
内部求作一点p,使pc=Pd,并且p点到
AOB两边的距离相等
0
C
D
B
A
知识的升华
独立
作业
P 31习题1.7 第2题.
祝你成功!
结束寄语
严格性之于数学家,犹如道德之于人.
证明的规范性在于:条理清晰,因果相应,言必有据.这是初学证明者谨记和遵循的原则.
下课了!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
