北师大版八年级下册数学 第六章 平行四边形复习课 课件(共17张PPT)
文档属性
| 名称 | 北师大版八年级下册数学 第六章 平行四边形复习课 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 430.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 22:07:05 | ||
图片预览





文档简介
第六章 平行四边形
复习课
一、平行四边形的概念与性质
1.两组对边分别_________的四边形叫做平行四边形.
2.平行四边形是_________对称图形,_________________是它的对称中心.
3.平行四边形的性质:(1)平行四边形的对边______________;(2)平行四边形的对角_________,
(邻角___________);(3)平行四边形的对角线_______________.
点拨:(1)平行四边形的对边的性质要从位置与数量两个方面考虑;(2)若一条直线过平行四边形的对角线的交点,那么这条直线等分平行四边形的面积.
知识归纳
平行
中心
两条对角线的交点
平行且相等
相等
互补
互相平分
平行
二、平行四边形的判定
1.从对边看:(1)两组对边分别_________的四边形叫做平行四边形;(2)两组对边分别____________的四边形是平行四边形;(3)一组对边______________的四边形是平行四边形.
2.从对角看:两组对角分别________的四边形是平行四边形.
3.从对角线看:对角线___________的四边形是平行四边形.
相等
平行且相等
相等
互相平分
知识归纳
三、三角形的中位线定理
1.连接三角形两边_________的线段叫做三角形的中位线.三角形中线是连接一顶点和它的对边中点的_______,而三角形中位线是连接三角形两边中点的_________.
2.三角形的中位线平行于_________并且等于它的________.
小贴士:中位线是三角形的一条重要线段,由于它的性质与线段的中点及平行线紧密相连,因此,它在几何图形的计算及证明中有着广泛的应用.
中点
线段
线段
第三边
平等
四、多边形的内角和与外角和
1.n边形的内角和等于_______________.
2.多边形内角的_______与另一边的___________组成的角叫做这个多边形的外角;在每个顶点处取一个外角,它们的和叫做这个多边形的外角和.
3.任意多边形的外角和等于________.
小贴士:(1)如果一个多边形的边数增加一条,那么这个多边形的内角和增加180°,外角和则不变,即任意多边形的外角和与多边形的边数无关;(2)在四边形的四个内角中,最多有3个钝角,最多有3个锐角.
(n-2)×180°
一边
反向延长线
360°
考点攻略
A
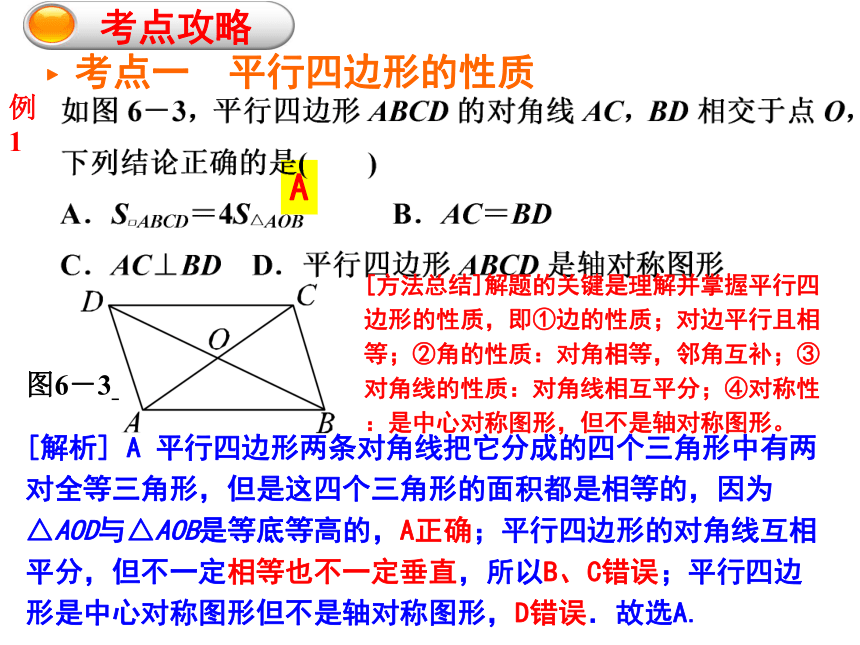
?考点一 平行四边形的性质
图6-3
[解析] A 平行四边形两条对角线把它分成的四个三角形中有两对全等三角形,但是这四个三角形的面积都是相等的,因为△AOD与△AOB是等底等高的,A正确;平行四边形的对角线互相平分,但不一定相等也不一定垂直,所以B、C错误;平行四边形是中心对称图形但不是轴对称图形,D错误.故选A.
[方法总结]解题的关键是理解并掌握平行四边形的性质,即①边的性质;对边平行且相等;②角的性质:对角相等,邻角互补;③对角线的性质:对角线相互平分;④对称性:是中心对称图形,但不是轴对称图形。
例
1
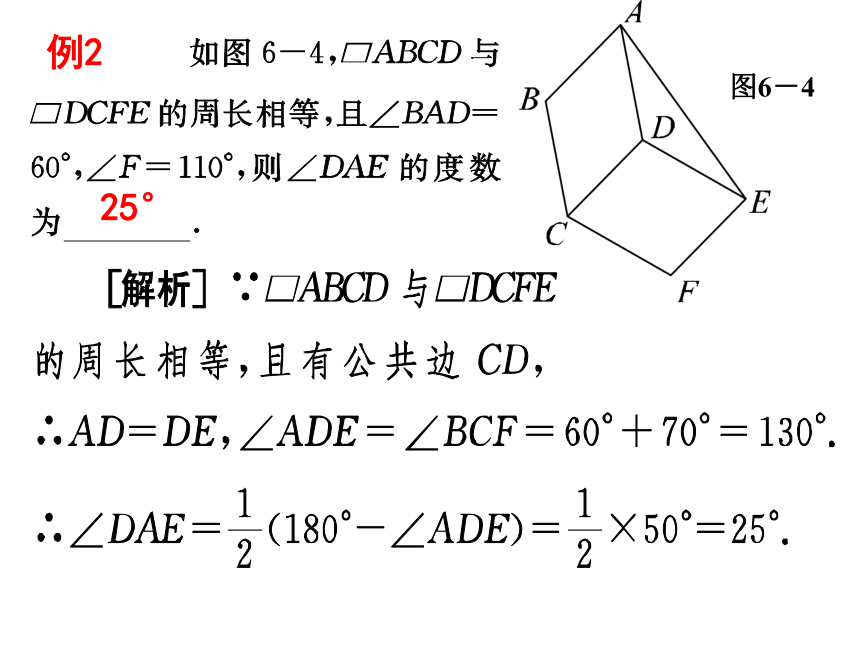
例2
图6-4
25°
?考点二 平行四边形的判定
如图6-5,在四边形ABCD中,AB∥CD,请你添加一个条件,使得四边形ABCD成为平行四边形,你添加的条件是________.
图6-5
[答案] 答案不唯一,如AD∥BC或∠A=∠C或∠B=∠D或∠A+∠B=180°
[解析] 要判断四边形ABCD是平行四边形,由一组对边平行且相等的四边形是平行四边形知,只需AB=CD即可.本题答案不唯一,只要符合条件即可,如AD∥BC或∠A=∠C或∠B=∠D或∠A+∠B=180°或∠C+∠D=180°等.
例3
?考点三 平行四边形性质与判定的综合
例4
图6-6
如图6-6,在Rt△ABC中,∠B=90°,AB=3,BC=4,点D在BC上,以AC为对角线的所有?ADCE中,DE最小的值是( )
A.2 B.3 C.4 D.5
B
[解析] B
∵四边形ADCE是平行四边形,
∴OD=OE,OA=OC.
∴当OD取最小值时,线段DE最短,
此时BC⊥DE.
∵AB⊥BC,∴AB∥DE.
又∵AE∥BC.
∴四边形ABDE是平行四边形.
∴ED=AB=3.故选B.
[方法规律]
本题考查了平行四边形的性质与判定及垂线段最短的性质,将原先求一线段最小值转化线段最短是解题关键。
例5
如图6-7,四边形ABCD是平行四边形,E,F是对角线AC上的两点,∠1=∠2.
求证:(1)AE=CF;
(2)四边形EBFD是平行四边形.
图6-7
证明:(1)(法一)
如图6-8①:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,∠3=∠4,
∵∠1=∠3+∠5,∠2=∠4+∠6,∠1=∠2,
∴∠5=∠6,
∴△ADE≌△CBF,∴AE=CF.
图6-8
[方法指导]
本题考查了全等三角形的判定与性质、平行四边形的判定与性质。平行四边形的判定方法共有五种,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法,充分分析题目条件,根据条件和学过的知识挖掘能够得到的结果,然后把所得到的结果充分联系起来即可解决问题。
(法二)如图6-8②,连接BD交AC于点O,在平行四边形ABCD中,OA=OC,OB=OD,
∵∠1=∠2,∠EOD=∠FOB,∴△DOE≌△BOF,∴OE=OF,∴OA-OE=OC-OF,即AE=CF.
(2)(法一)如图①,∵∠1=∠2,∴DE∥BF,
∵△ADE≌△CBF,∴DE=BF,
∴四边形EBFD是平行四边形.
(法二)如图②,∵OE=OF,OB=OD,
∴四边形EBFD是平行四边形.
例6、在?ABCD中,点O是对角线AC,BD的交点,点E是边CD的中点,且AB=6,BC=10,则OE=________.
5
图6-11
?考点四 三角形的中位线
[方法规律]本题考查了平行四边形的性质及三角形中位线定理,理解的关键是掌握平行四边形的对角线互相平分与三角形的中位线定理。
[方法规律]在应用多边形的内角和与外角和定理时要正确把握内角和公式为(n-2)·180°,外角和为360°。
?考点七 多边形的内角和与外角和
例7若一个多边形的内角和等于外角和的3倍,求这个多边形的边数.
[解析] 根据多边形的外角和为360°,内角和公式为(n-2)·180°,由题意可知内角和=3×外角和,设出未知数,可得到方程,解方程即可.
解:设这个多边形是n边形,由题意,得
(n-2)×180°=360°×3,
解得n=8.
答:这个多边形的边数是8.
例8下列各角能成为某多边形的内角和的只有( )
A.280° B.580° C.1800° D.2000°
[解析] C 多边形的内角和为(n-2)·180°,即任意一个多边形的内角和都能被180整除,A,B,C,D四个选项中只有1800°能被180°整除.故选C.
C
针对训练1
C
如图6-14所示,吴伯伯家一块等边三角形的空地ABC,已知点E,F分别是边AB,AC的中点,量得EF=5米,他想把四边形BCFE用篱笆围成一圈放养小鸡,则需要篱笆的长是( )
A.15米 B.20米 C.25米 D.30米
图6-14
针对训练2
图6-16
如图6-16,△ABC是等边三角形,点D,F分别在线段BC,AB上,∠EFB=60°,DC=EF.
(1)求证:四边形EFCD是平行四边形;
(2)若BF=EF,求证:AE=AD.
图6-17
证明:(1)∵△ABC是等边三角形,∴∠ABC=60°.又∵∠EFB=60°,∴∠ABC=∠EFB,∴EF∥BC,又∵DC=EF,∴四边形EFCD是平行四边形.
(2)连接BE.
∵∠EFB=60°,BF=EF,∴△BEF为等边三角形,∴BE=BF=EF,∠ABE=60°.
∵CD=EF,∴BE=CD,又∵△ABC为等边三角形,∴AB=AC,∠ACD=60°,∴∠ABE=∠ACD,在△ABE和△ACD中,∵BE=CD,∠ABE=∠ACD,AB=AC,∴△ABE≌△ACD(SAS),∴AE=AD.
复习课
一、平行四边形的概念与性质
1.两组对边分别_________的四边形叫做平行四边形.
2.平行四边形是_________对称图形,_________________是它的对称中心.
3.平行四边形的性质:(1)平行四边形的对边______________;(2)平行四边形的对角_________,
(邻角___________);(3)平行四边形的对角线_______________.
点拨:(1)平行四边形的对边的性质要从位置与数量两个方面考虑;(2)若一条直线过平行四边形的对角线的交点,那么这条直线等分平行四边形的面积.
知识归纳
平行
中心
两条对角线的交点
平行且相等
相等
互补
互相平分
平行
二、平行四边形的判定
1.从对边看:(1)两组对边分别_________的四边形叫做平行四边形;(2)两组对边分别____________的四边形是平行四边形;(3)一组对边______________的四边形是平行四边形.
2.从对角看:两组对角分别________的四边形是平行四边形.
3.从对角线看:对角线___________的四边形是平行四边形.
相等
平行且相等
相等
互相平分
知识归纳
三、三角形的中位线定理
1.连接三角形两边_________的线段叫做三角形的中位线.三角形中线是连接一顶点和它的对边中点的_______,而三角形中位线是连接三角形两边中点的_________.
2.三角形的中位线平行于_________并且等于它的________.
小贴士:中位线是三角形的一条重要线段,由于它的性质与线段的中点及平行线紧密相连,因此,它在几何图形的计算及证明中有着广泛的应用.
中点
线段
线段
第三边
平等
四、多边形的内角和与外角和
1.n边形的内角和等于_______________.
2.多边形内角的_______与另一边的___________组成的角叫做这个多边形的外角;在每个顶点处取一个外角,它们的和叫做这个多边形的外角和.
3.任意多边形的外角和等于________.
小贴士:(1)如果一个多边形的边数增加一条,那么这个多边形的内角和增加180°,外角和则不变,即任意多边形的外角和与多边形的边数无关;(2)在四边形的四个内角中,最多有3个钝角,最多有3个锐角.
(n-2)×180°
一边
反向延长线
360°
考点攻略
A
?考点一 平行四边形的性质
图6-3
[解析] A 平行四边形两条对角线把它分成的四个三角形中有两对全等三角形,但是这四个三角形的面积都是相等的,因为△AOD与△AOB是等底等高的,A正确;平行四边形的对角线互相平分,但不一定相等也不一定垂直,所以B、C错误;平行四边形是中心对称图形但不是轴对称图形,D错误.故选A.
[方法总结]解题的关键是理解并掌握平行四边形的性质,即①边的性质;对边平行且相等;②角的性质:对角相等,邻角互补;③对角线的性质:对角线相互平分;④对称性:是中心对称图形,但不是轴对称图形。
例
1
例2
图6-4
25°
?考点二 平行四边形的判定
如图6-5,在四边形ABCD中,AB∥CD,请你添加一个条件,使得四边形ABCD成为平行四边形,你添加的条件是________.
图6-5
[答案] 答案不唯一,如AD∥BC或∠A=∠C或∠B=∠D或∠A+∠B=180°
[解析] 要判断四边形ABCD是平行四边形,由一组对边平行且相等的四边形是平行四边形知,只需AB=CD即可.本题答案不唯一,只要符合条件即可,如AD∥BC或∠A=∠C或∠B=∠D或∠A+∠B=180°或∠C+∠D=180°等.
例3
?考点三 平行四边形性质与判定的综合
例4
图6-6
如图6-6,在Rt△ABC中,∠B=90°,AB=3,BC=4,点D在BC上,以AC为对角线的所有?ADCE中,DE最小的值是( )
A.2 B.3 C.4 D.5
B
[解析] B
∵四边形ADCE是平行四边形,
∴OD=OE,OA=OC.
∴当OD取最小值时,线段DE最短,
此时BC⊥DE.
∵AB⊥BC,∴AB∥DE.
又∵AE∥BC.
∴四边形ABDE是平行四边形.
∴ED=AB=3.故选B.
[方法规律]
本题考查了平行四边形的性质与判定及垂线段最短的性质,将原先求一线段最小值转化线段最短是解题关键。
例5
如图6-7,四边形ABCD是平行四边形,E,F是对角线AC上的两点,∠1=∠2.
求证:(1)AE=CF;
(2)四边形EBFD是平行四边形.
图6-7
证明:(1)(法一)
如图6-8①:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,∠3=∠4,
∵∠1=∠3+∠5,∠2=∠4+∠6,∠1=∠2,
∴∠5=∠6,
∴△ADE≌△CBF,∴AE=CF.
图6-8
[方法指导]
本题考查了全等三角形的判定与性质、平行四边形的判定与性质。平行四边形的判定方法共有五种,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法,充分分析题目条件,根据条件和学过的知识挖掘能够得到的结果,然后把所得到的结果充分联系起来即可解决问题。
(法二)如图6-8②,连接BD交AC于点O,在平行四边形ABCD中,OA=OC,OB=OD,
∵∠1=∠2,∠EOD=∠FOB,∴△DOE≌△BOF,∴OE=OF,∴OA-OE=OC-OF,即AE=CF.
(2)(法一)如图①,∵∠1=∠2,∴DE∥BF,
∵△ADE≌△CBF,∴DE=BF,
∴四边形EBFD是平行四边形.
(法二)如图②,∵OE=OF,OB=OD,
∴四边形EBFD是平行四边形.
例6、在?ABCD中,点O是对角线AC,BD的交点,点E是边CD的中点,且AB=6,BC=10,则OE=________.
5
图6-11
?考点四 三角形的中位线
[方法规律]本题考查了平行四边形的性质及三角形中位线定理,理解的关键是掌握平行四边形的对角线互相平分与三角形的中位线定理。
[方法规律]在应用多边形的内角和与外角和定理时要正确把握内角和公式为(n-2)·180°,外角和为360°。
?考点七 多边形的内角和与外角和
例7若一个多边形的内角和等于外角和的3倍,求这个多边形的边数.
[解析] 根据多边形的外角和为360°,内角和公式为(n-2)·180°,由题意可知内角和=3×外角和,设出未知数,可得到方程,解方程即可.
解:设这个多边形是n边形,由题意,得
(n-2)×180°=360°×3,
解得n=8.
答:这个多边形的边数是8.
例8下列各角能成为某多边形的内角和的只有( )
A.280° B.580° C.1800° D.2000°
[解析] C 多边形的内角和为(n-2)·180°,即任意一个多边形的内角和都能被180整除,A,B,C,D四个选项中只有1800°能被180°整除.故选C.
C
针对训练1
C
如图6-14所示,吴伯伯家一块等边三角形的空地ABC,已知点E,F分别是边AB,AC的中点,量得EF=5米,他想把四边形BCFE用篱笆围成一圈放养小鸡,则需要篱笆的长是( )
A.15米 B.20米 C.25米 D.30米
图6-14
针对训练2
图6-16
如图6-16,△ABC是等边三角形,点D,F分别在线段BC,AB上,∠EFB=60°,DC=EF.
(1)求证:四边形EFCD是平行四边形;
(2)若BF=EF,求证:AE=AD.
图6-17
证明:(1)∵△ABC是等边三角形,∴∠ABC=60°.又∵∠EFB=60°,∴∠ABC=∠EFB,∴EF∥BC,又∵DC=EF,∴四边形EFCD是平行四边形.
(2)连接BE.
∵∠EFB=60°,BF=EF,∴△BEF为等边三角形,∴BE=BF=EF,∠ABE=60°.
∵CD=EF,∴BE=CD,又∵△ABC为等边三角形,∴AB=AC,∠ACD=60°,∴∠ABE=∠ACD,在△ABE和△ACD中,∵BE=CD,∠ABE=∠ACD,AB=AC,∴△ABE≌△ACD(SAS),∴AE=AD.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
