北师大版八年级下册数学 3.3 中心对称教学课件 (共16张PPT)
文档属性
| 名称 | 北师大版八年级下册数学 3.3 中心对称教学课件 (共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 23:12:28 | ||
图片预览


文档简介
B
A
E
C
D
D
E
C
3.3.中心对称
观 察
O
C
B
(2)
重合
重合
观察下面的2组图形,看一看各组中2个图形的形状、大小是否相同?
怎样将一个图形旋转得到另一个图形?
180°
180°
把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,
C
B
认识新朋友
这个点叫做对称中心
这两个图形在旋转中能重合的对应点叫做关于中心的对称点.
180°
O
C
B
(2)
△OCD和△OAB关于 对称,对称中心是 .
点C和 是关于O的对称点;
点B和 是关于O的对称点
两只小鱼关于 成中心对称,
对称中心是 .
探究一:观察两个图形你发现了什么?
O
●
A′
C′
B′
C
A
B
探究二:分别连接对称点AA′,BB′,CC′,你又发现
了什么?
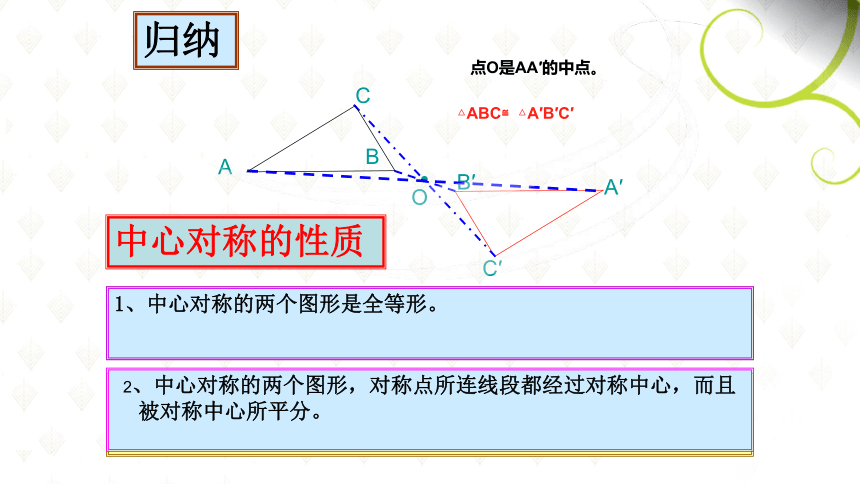
点O是AA′的中点。
△ABC≌△A′B′C′
探究
归纳
2、中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分。
中心对称的性质
1、中心对称的两个图形是全等形。
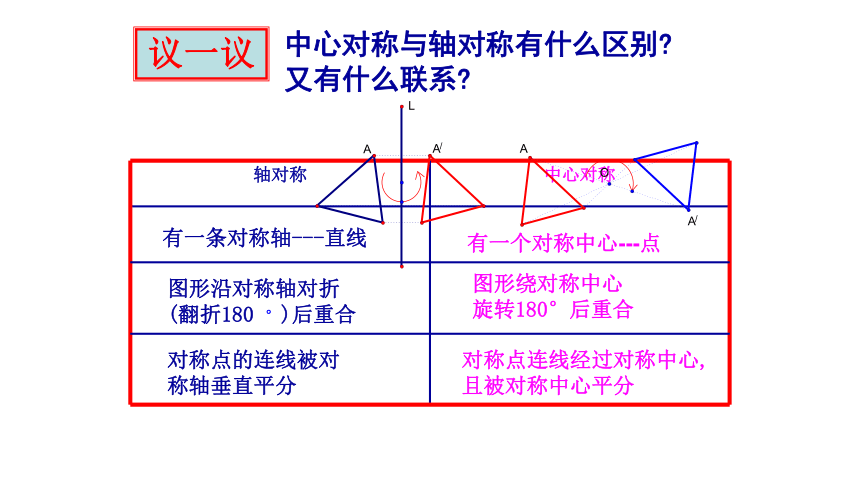
议一议
中心对称与轴对称有什么区别?
又有什么联系?
轴对称
中心对称
有一条对称轴---直线
有一个对称中心---点
图形沿对称轴对折(翻折180 °)后重合
图形绕对称中心旋转180°后重合
对称点的连线被对称轴垂直平分
对称点连线经过对称中心,且被对称中心平分
1、判断正误:
(1)轴对称的两个图形一定是全等形,但全等的两个图形
不一定是轴对称的图形。( )
(2)成中心对称的两个图形一定是全等形。但全等的两个
图形不一定是成中心对称的图形。 ( )
(3)全等的两个图形,不是成中心对称的图形,就是成轴
对称的图形。 ( )
2、选择题:
如果两个图形成中心对称,下列说法正确的是 ( )
(1)对称点连线必经过对称中心,且被对称中心平分。
(2)这两个图形一定是全等形。
(3)把一个图形绕着对称中心旋转后定与另一个图形重合。
(A)(1)(2)(3)(B)(2)(3)
(C)(1)(3) (D)(1)(2)
√
√
×
D
O
●
A′
C′
B′
A′
C′
B′
B
O
A
A′
灵活运用,体会内涵
点A′即为所求的点
已知A点和O点,画出点A关于点O的对称点A'
已知线段AB和O点,画出线段AB关于点O 的对称线段A'B'
例1、
C
A′
已知△ABC和O点,画出与 △ABC关于点O对称的△A′B′C′.
(不要求写画法)
如图,D是△ABC的边AC上一点,画出△EFG,使它与△ ABC关于D成中心对称.
B
C
A
D
随堂练习
1.如图,已知△ABC与△A′B′C′中心对称,求出它们的对称中心O.
A
B
C
A′
B′
C′
练 习
◆你在这堂课中获得哪些知识?
◆你还有疑问吗?
探究
分析
归纳
中心对称的定义
中心对称的性质
观察
转 化 思 想
作业
选择一个你喜欢的图形,再找一点,
画图形使两个图形关于这个点成中心对称。
A
E
C
D
D
E
C
3.3.中心对称
观 察
O
C
B
(2)
重合
重合
观察下面的2组图形,看一看各组中2个图形的形状、大小是否相同?
怎样将一个图形旋转得到另一个图形?
180°
180°
把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,
C
B
认识新朋友
这个点叫做对称中心
这两个图形在旋转中能重合的对应点叫做关于中心的对称点.
180°
O
C
B
(2)
△OCD和△OAB关于 对称,对称中心是 .
点C和 是关于O的对称点;
点B和 是关于O的对称点
两只小鱼关于 成中心对称,
对称中心是 .
探究一:观察两个图形你发现了什么?
O
●
A′
C′
B′
C
A
B
探究二:分别连接对称点AA′,BB′,CC′,你又发现
了什么?
点O是AA′的中点。
△ABC≌△A′B′C′
探究
归纳
2、中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分。
中心对称的性质
1、中心对称的两个图形是全等形。
议一议
中心对称与轴对称有什么区别?
又有什么联系?
轴对称
中心对称
有一条对称轴---直线
有一个对称中心---点
图形沿对称轴对折(翻折180 °)后重合
图形绕对称中心旋转180°后重合
对称点的连线被对称轴垂直平分
对称点连线经过对称中心,且被对称中心平分
1、判断正误:
(1)轴对称的两个图形一定是全等形,但全等的两个图形
不一定是轴对称的图形。( )
(2)成中心对称的两个图形一定是全等形。但全等的两个
图形不一定是成中心对称的图形。 ( )
(3)全等的两个图形,不是成中心对称的图形,就是成轴
对称的图形。 ( )
2、选择题:
如果两个图形成中心对称,下列说法正确的是 ( )
(1)对称点连线必经过对称中心,且被对称中心平分。
(2)这两个图形一定是全等形。
(3)把一个图形绕着对称中心旋转后定与另一个图形重合。
(A)(1)(2)(3)(B)(2)(3)
(C)(1)(3) (D)(1)(2)
√
√
×
D
O
●
A′
C′
B′
A′
C′
B′
B
O
A
A′
灵活运用,体会内涵
点A′即为所求的点
已知A点和O点,画出点A关于点O的对称点A'
已知线段AB和O点,画出线段AB关于点O 的对称线段A'B'
例1、
C
A′
已知△ABC和O点,画出与 △ABC关于点O对称的△A′B′C′.
(不要求写画法)
如图,D是△ABC的边AC上一点,画出△EFG,使它与△ ABC关于D成中心对称.
B
C
A
D
随堂练习
1.如图,已知△ABC与△A′B′C′中心对称,求出它们的对称中心O.
A
B
C
A′
B′
C′
练 习
◆你在这堂课中获得哪些知识?
◆你还有疑问吗?
探究
分析
归纳
中心对称的定义
中心对称的性质
观察
转 化 思 想
作业
选择一个你喜欢的图形,再找一点,
画图形使两个图形关于这个点成中心对称。
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
