北师大版七年级数学下册 4.4 《用尺规作三角形》教学课件(共23张PPT)
文档属性
| 名称 | 北师大版七年级数学下册 4.4 《用尺规作三角形》教学课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 139.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 23:20:11 | ||
图片预览




文档简介
第四章三角形
4.4用尺规作三角形
学习目标
1.在分别给出两边夹角,两角夹边和三边的条件下,能够用尺规作出三角形,进一步学习尺规作图的步骤;
2.会用尺规作出符合条件要求的三角形.
1.复习用尺规作一条线段等于已知线段,作一个角等于已知角.
2.提出问题:边和角是三角形的基本元素,你能根据一些特殊的边角关系用尺规作出三角形吗?
复习巩固
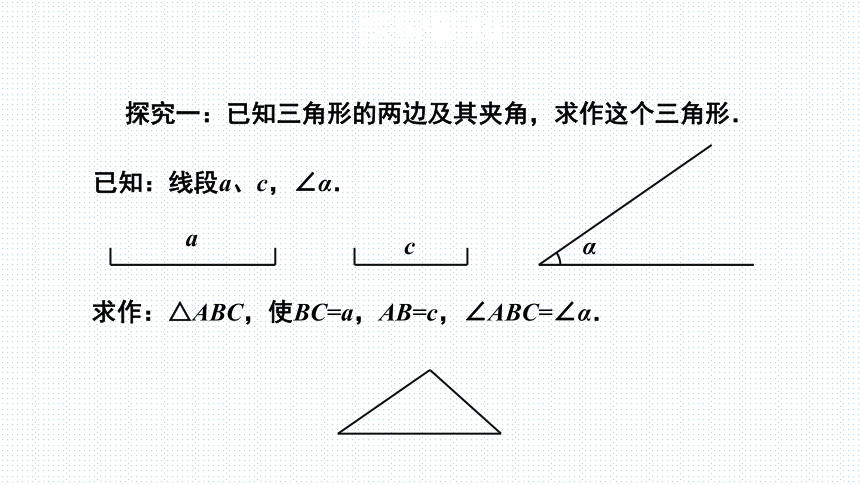
探究一:已知三角形的两边及其夹角,求作这个三角形.
已知:线段a、c,∠α.
求作:△ABC,使BC=a,AB=c,∠ABC=∠α.
a
c
α
探究新知
作法:
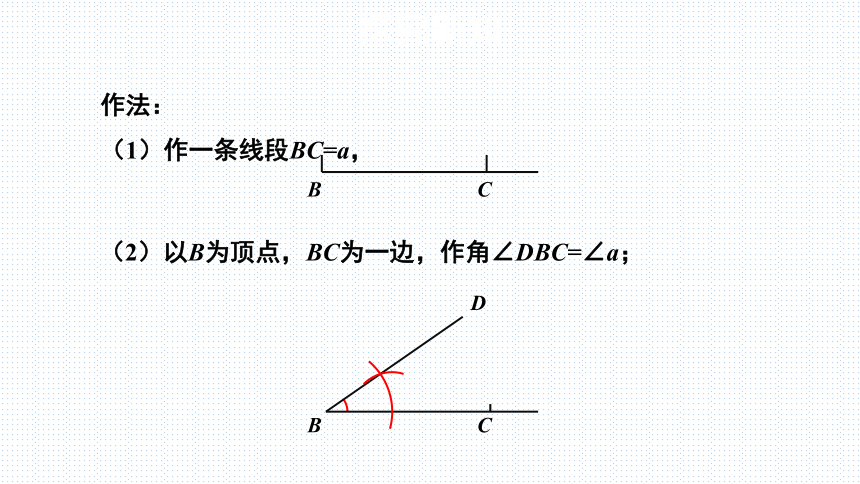
(1)作一条线段BC=a,
B
C
(2)以B为顶点,BC为一边,作角∠DBC=∠a;
B
C
D
探究新知
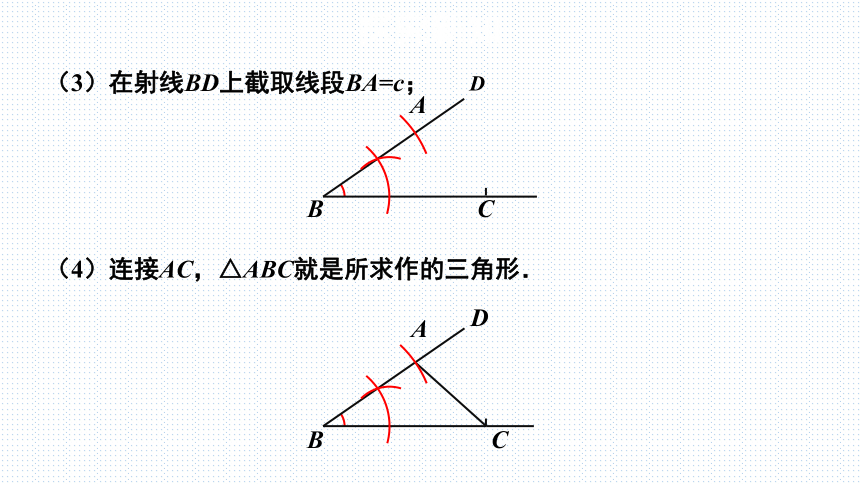
(3)在射线BD上截取线段BA=c;
B
C
D
A
(4)连接AC,△ABC就是所求作的三角形.
B
C
D
A
探究新知
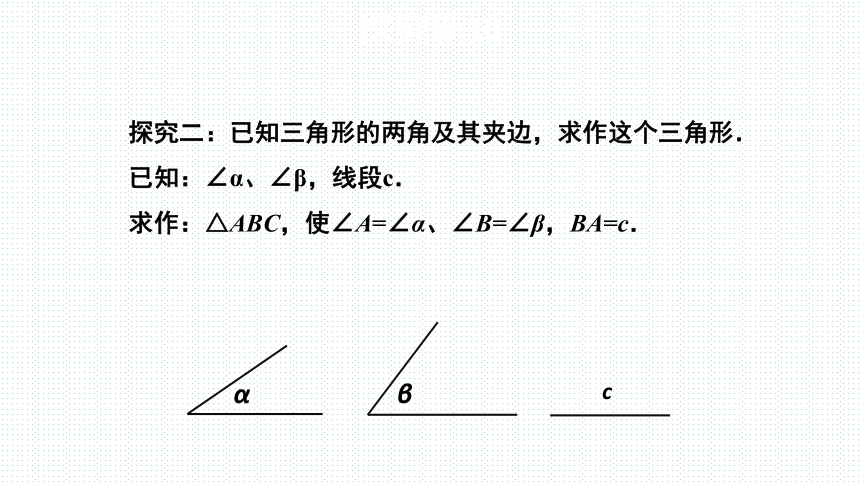
探究二:已知三角形的两角及其夹边,求作这个三角形.
已知:线段∠α,∠β,线段c .
求作:△ABC,使得∠A=∠α,∠B=∠β,AB=c.
α
β
c
探究新知
探究二:已知三角形的两角及其夹边,求作这个三角形.
已知:∠α、∠β,线段c.
求作:△ABC,使∠A=∠α、∠B=∠β,BA=c.
α
β
c
探究新知
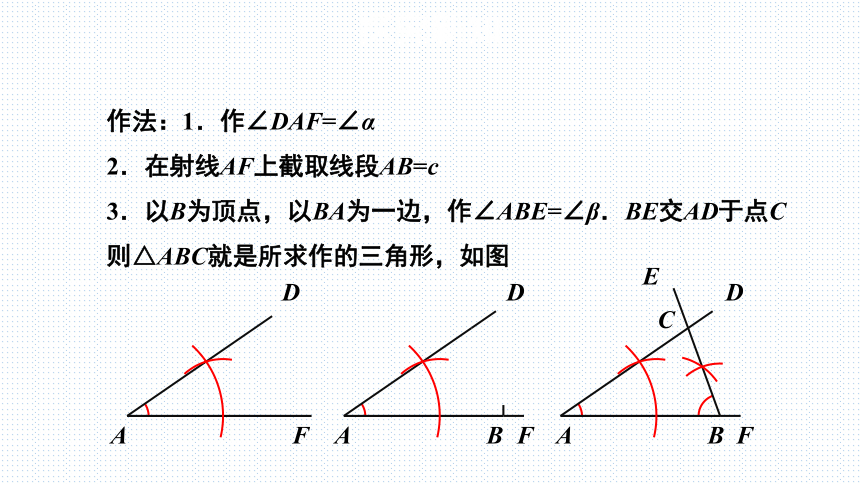
作法:1.作∠DAF=∠α
2.在射线AF上截取线段AB=c
3.以B为顶点,以BA为一边,作∠ABE=∠β.BE交AD于点C
则△ABC就是所求作的三角形,如图
D
A
F
D
A
F
D
A
F
B
B
E
C
探究新知
探究三:已知三角形的三边,求作这个三角形.
已知:线段a,b,c.
求作:△ABC,使得AB=c,AC=b,BC=a.
a
b
c
探究新知
作法:1.作线段BC=a;
2.以点C为圆心,以b为半径画弧,再以B为圆心,以c为半径画弧,两弧相交于点A;
3.连接AC和AB,则△ABC即为所求作的三角形,如图所示.
A
B
C
探究新知
方法总结:已知三角形三边的长,根据全等三角形的判定“SSS”,知三角形的形状和大小也就确定了.作三角形相当于确定三角形三个顶点的位置.因此可先确定三角形的一条边(即两个顶点),再分别以这条边的两个端点为圆心,以已知线段长为半径画弧,两弧的交点即为另一个顶点.
探究新知
例1 已知,三角形的两条边分别是3cm和4cm,且3cm这条边所对的角是30°,求作这个三角形.
分析:先作一个30°角,再作出它的一个邻边,只要再把三角形30°角所对的边确定了,所作的三角形就确定了.
典型例题
解:(1)作30°角;
(2)截AB=4cm;
(3)以B为圆心,以3cm为半径画弧,交30°角的一边于C、 C′点;
(4)连接BC、BC′,得到的△ABC和△ABC′都是符合要求的三角形.
B
A
C
C′
30°
4cm
典型例题
例2 已知:∠α和线段c,
求作:△ABC,使得∠B=∠α,∠A=2∠α,AB=c.
c
α
分析:本题是已知三角形的两角及其夹边,求作这个三角形.关键是∠A的作法,∠A=2∠α,可以先以AB为一条边,作∠PAB=∠α,再以PA为一条边,作∠PAQ=∠α,则∠QAB=2∠α.
典型例题
解:(1)作线段AB=c;
(2)以B为顶点,以BA为一条边,作∠MBA=∠α;
(3)在AB的同侧,以A为顶点,以AB为一条边,作∠QAB=2∠α,射线BM、AQ相交于点C.则△ABC即为所求作的三角形.
A
B
M
Q
C
典型例题
例3 已知线段a、b,求作△ABC ,使得∠C=90°,BC=a,AC=b.
解:作法:(1)作∠PCQ=90°;
(2)在PC、QC上分别截取线段BC=a,AC=b;
(3)连接AB.则△ABC即为所求作的三角形.
A
B
C
P
Q
a
b
典型例题
解:作法:根据三角形内角和等于180°,可求得该三角形的另一个角是70°.
(1)作线段AB=3cm.
(2)以AB为边,分别以A、B为顶点作∠A=50°, ∠B=70°.
(3)∠A、∠B的另一边交于C点,则△ABC就是所求作的三角形.
C
A
B
50°
70°
典型例题
例4 已知,三角形的两个内角分别是50°和60°,其中60°角所对的边是3cm,求作这个三角形.
随堂练习
1.用直尺和圆规作一个角等于已知角的示意图如图所示,则说明∠A′O′B′=∠AOB的依据是 ( )
A.SSS D.SAS C.ASA D.AAS
A
2.已知:任画一条线段a.
求作:等腰三角形(两腰长相等),使底边长为2a,腰长为3a.
a
随堂练习
解:(1)作线段BC=2a;
(2)分别以B,C为圆心,3a长为半径在BC同侧画弧,两弧的一个交点为A;
(3)连接AC,AB.△ABC就是所求作的三角形.
A
B
C
随堂练习
(一)明确尺规作图的三个基本类型:
1.已知两边及其夹角作三角形;
2.已知两角及其夹边作三角形;
3.已知三边作三角形;
(二)熟练尺规作图的基本作法步骤.
课堂小结
再见
4.4用尺规作三角形
学习目标
1.在分别给出两边夹角,两角夹边和三边的条件下,能够用尺规作出三角形,进一步学习尺规作图的步骤;
2.会用尺规作出符合条件要求的三角形.
1.复习用尺规作一条线段等于已知线段,作一个角等于已知角.
2.提出问题:边和角是三角形的基本元素,你能根据一些特殊的边角关系用尺规作出三角形吗?
复习巩固
探究一:已知三角形的两边及其夹角,求作这个三角形.
已知:线段a、c,∠α.
求作:△ABC,使BC=a,AB=c,∠ABC=∠α.
a
c
α
探究新知
作法:
(1)作一条线段BC=a,
B
C
(2)以B为顶点,BC为一边,作角∠DBC=∠a;
B
C
D
探究新知
(3)在射线BD上截取线段BA=c;
B
C
D
A
(4)连接AC,△ABC就是所求作的三角形.
B
C
D
A
探究新知
探究二:已知三角形的两角及其夹边,求作这个三角形.
已知:线段∠α,∠β,线段c .
求作:△ABC,使得∠A=∠α,∠B=∠β,AB=c.
α
β
c
探究新知
探究二:已知三角形的两角及其夹边,求作这个三角形.
已知:∠α、∠β,线段c.
求作:△ABC,使∠A=∠α、∠B=∠β,BA=c.
α
β
c
探究新知
作法:1.作∠DAF=∠α
2.在射线AF上截取线段AB=c
3.以B为顶点,以BA为一边,作∠ABE=∠β.BE交AD于点C
则△ABC就是所求作的三角形,如图
D
A
F
D
A
F
D
A
F
B
B
E
C
探究新知
探究三:已知三角形的三边,求作这个三角形.
已知:线段a,b,c.
求作:△ABC,使得AB=c,AC=b,BC=a.
a
b
c
探究新知
作法:1.作线段BC=a;
2.以点C为圆心,以b为半径画弧,再以B为圆心,以c为半径画弧,两弧相交于点A;
3.连接AC和AB,则△ABC即为所求作的三角形,如图所示.
A
B
C
探究新知
方法总结:已知三角形三边的长,根据全等三角形的判定“SSS”,知三角形的形状和大小也就确定了.作三角形相当于确定三角形三个顶点的位置.因此可先确定三角形的一条边(即两个顶点),再分别以这条边的两个端点为圆心,以已知线段长为半径画弧,两弧的交点即为另一个顶点.
探究新知
例1 已知,三角形的两条边分别是3cm和4cm,且3cm这条边所对的角是30°,求作这个三角形.
分析:先作一个30°角,再作出它的一个邻边,只要再把三角形30°角所对的边确定了,所作的三角形就确定了.
典型例题
解:(1)作30°角;
(2)截AB=4cm;
(3)以B为圆心,以3cm为半径画弧,交30°角的一边于C、 C′点;
(4)连接BC、BC′,得到的△ABC和△ABC′都是符合要求的三角形.
B
A
C
C′
30°
4cm
典型例题
例2 已知:∠α和线段c,
求作:△ABC,使得∠B=∠α,∠A=2∠α,AB=c.
c
α
分析:本题是已知三角形的两角及其夹边,求作这个三角形.关键是∠A的作法,∠A=2∠α,可以先以AB为一条边,作∠PAB=∠α,再以PA为一条边,作∠PAQ=∠α,则∠QAB=2∠α.
典型例题
解:(1)作线段AB=c;
(2)以B为顶点,以BA为一条边,作∠MBA=∠α;
(3)在AB的同侧,以A为顶点,以AB为一条边,作∠QAB=2∠α,射线BM、AQ相交于点C.则△ABC即为所求作的三角形.
A
B
M
Q
C
典型例题
例3 已知线段a、b,求作△ABC ,使得∠C=90°,BC=a,AC=b.
解:作法:(1)作∠PCQ=90°;
(2)在PC、QC上分别截取线段BC=a,AC=b;
(3)连接AB.则△ABC即为所求作的三角形.
A
B
C
P
Q
a
b
典型例题
解:作法:根据三角形内角和等于180°,可求得该三角形的另一个角是70°.
(1)作线段AB=3cm.
(2)以AB为边,分别以A、B为顶点作∠A=50°, ∠B=70°.
(3)∠A、∠B的另一边交于C点,则△ABC就是所求作的三角形.
C
A
B
50°
70°
典型例题
例4 已知,三角形的两个内角分别是50°和60°,其中60°角所对的边是3cm,求作这个三角形.
随堂练习
1.用直尺和圆规作一个角等于已知角的示意图如图所示,则说明∠A′O′B′=∠AOB的依据是 ( )
A.SSS D.SAS C.ASA D.AAS
A
2.已知:任画一条线段a.
求作:等腰三角形(两腰长相等),使底边长为2a,腰长为3a.
a
随堂练习
解:(1)作线段BC=2a;
(2)分别以B,C为圆心,3a长为半径在BC同侧画弧,两弧的一个交点为A;
(3)连接AC,AB.△ABC就是所求作的三角形.
A
B
C
随堂练习
(一)明确尺规作图的三个基本类型:
1.已知两边及其夹角作三角形;
2.已知两角及其夹边作三角形;
3.已知三边作三角形;
(二)熟练尺规作图的基本作法步骤.
课堂小结
再见
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
