北师大版七年级数学下册 6.2 《频率的稳定性第1课时》教学课件(共31张PPT)
文档属性
| 名称 | 北师大版七年级数学下册 6.2 《频率的稳定性第1课时》教学课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 393.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 21:18:55 | ||
图片预览











文档简介
第六章 概率初步
6.2 频率的稳定性
第1课时
学习目标
通过掷图钉活动,感受在试验次数很多时,随机事件发生的频率具有稳定性.
理解频率的定义.
抛掷一枚图钉,落地后会
出现两种情况:钉尖朝上 ,
钉尖朝下。你认为钉尖朝上和
钉尖朝下的可能性一样
大吗?
小明和小丽在玩抛图钉游戏
问题情境
直觉告诉我任意掷一枚图钉,钉尖朝上和钉尖朝下的可能性是不相同的.
我的直觉跟你一样,但我不知道对不对.
不妨让我们用试验来验证吧!
问题情境
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}试验总次数
?
钉尖朝上次数
?
钉尖朝下次数
?
钉尖朝上频率(钉尖朝上次数/试验总次数)
?
钉尖朝下频率(钉尖朝下次数/试验总次数)
?
频率定义:在n次重复试验中,不确定事件A发生了m次,则比值 称为事件发生的频率.
探究新知
(1)两人一组做20次掷图钉游戏,并将数据记录在下表中:
(2)累计全班同学的试验结果,并将试验数据汇总填入下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}试验总次数n
20
40
80
120
160
200
240
280
320
360
400
钉尖朝上次数m
?
?
?
?
?
?
?
?
?
?
?
钉尖朝上频率m/n
?
?
?
?
?
?
?
?
?
?
?
探究新知
(3)请同学们根据已填的表格,完成下面的折线统计图
探究新知
20
40
80
120
200
240
160
320
280
0.2
400
360
1.0
0.6
0.8
0.4
钉尖朝上的频率
试验总次数
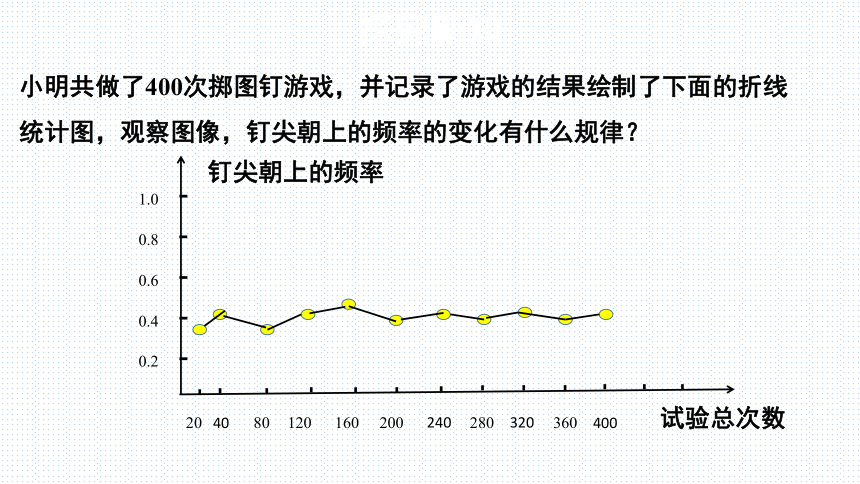
小明共做了400次掷图钉游戏,并记录了游戏的结果绘制了下面的折线统计图,观察图像,钉尖朝上的频率的变化有什么规律?
探究新知
探究新知
(4)观察图像,钉尖朝上的频率的变化有什么规律?
结论:在试验次数很大时,钉尖朝上的频率都会在一个常数附近摆动,即钉尖朝上的频率具有稳定性
探究新知
议一议:
(1)通过上面的试验,你认为针尖朝上和针尖朝下的可能性一样大吗?你是怎么想的?
(2)小军与小凡一起做了1000次掷图钉的试验,其中有640次针尖朝上,据此,他们认为针尖朝上的可能性比针尖朝下的可能性大,你同意他的说法吗?
人们在长期的实践中发现,在随机试验中,
由于众多微小的偶然因素的影响,每次测
得的结果虽不尽相同,但大量重复试验所
得结果却能反应客观规律.
频率的稳定性是由瑞士数学家雅布·伯努利(1654-1705)最早阐明的,他还提出了由频率可以估计事件发生的可能性大小.
频率稳定性定理
数学史实
典型例题
例1.(1)掷一枚质地均匀的硬币10次,下列说法正确的是 ( )
A.每两次必有1次正面向上 B.可能有5次正面向上
C.必有5次正面向上 D.不可能有10次正面向上
(2)某种彩票的中奖机会是1%,下列说法正确的是 ( )
A.买一张这种彩票一定不会中奖
B.买一张这种彩票一定会中奖
C.买100张这种彩票一定会中奖
D.当购买彩票的数量很大时,中奖的频率稳定在1%
B
D
典型例题
(3)在做图钉落地的试验中,正确的是 ( )
A.甲做了4000次,得出钉尖触地的机会约为46%,于是他断定在做第4001次时,
钉尖肯定不会触地
B.乙认为一次一次做,速度太慢,他拿来了大把材料,形状及大小都完全一样的图钉,随意朝上轻轻抛出,然后统计钉尖触地的次数,这样大大提高了速度
C.老师安排每位同学回家做试验,图钉自由选取
D.老师安排同学回家做试验,图钉统一发(完全一样的图钉).同学交来的结果,老师挑选他满意的进行统计,他不满意的就不要
B
典型例题
(4)一个不透明的盒子里有n个除颜色外其他完全相同的小球,其中有6个黄球.每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后再放回盒子,通过大量重复摸球试验后发现,摸到黄球的频率稳定在30%,那么可以推算出n大约是 ( )
A.6 B.10 C.18 D.20
D
例2.王老师将1个黑球和若干个白球放入一个不透明的口袋并搅匀,让若干学生进行摸球试验,每次摸出一个球(有放回),下表是活动进行中的一组统计数据(结果保留两位小数):
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}摸球的次数n
100
150
200
500
800
1000
摸到黑球的次数m
23
31
60
130
203
251
摸到黑球的频率
0.23
0.21
0.30
0.26
0.25
____
典型例题
(1)补全上表中的有关数据,根据上表数据估计从袋中摸出一个球是黑球的概率是________;
(2)估算袋中白球的个数.
解:(1)251÷1000≈0.25.∵大量重复试验事件发生的频率逐渐稳定到0.25附近,∴估计从袋中摸出一个球是黑球的概率是0.25;
(2)设袋中白球为x个, =0.25,x=3.
答:估计袋中有3个白球.
典型例题
典型例题
例3. 某批篮球质量检验结果如下:
抽取的篮球数n
400
600
800
1000
1200
优等品频数m
376
570
744
940
1128
优等品频率m/n
0.94
____
____
____
____
(1)填写表中优等品的频率;
(2)这批篮球优等品的概率估计值是多少?
典型例题
解:(1) =0.95, =0.93, =0.94, =0.94,
故表中依次填0.95,0.93,0.94,0.94;
(2)这批篮球优等品的概率估计值是0.94.
1.(1)某校男生中,若随机抽取若干名同学做“是否喜欢足球”的问卷调查,抽到喜欢足球的同学的频率是 ,这个 的含义是( ).
A.只发出5份调查卷,其中三份是喜欢足球的答卷
B.在答卷中,喜欢足球的答卷与总问卷的比为3︰8
C.在答卷中,喜欢足球的答卷占总答卷的
D.在答卷中,每抽出100份问卷,恰有60份答卷是喜欢足球
5
3
—
5
3
—
C
5
3
—
随堂练习
随堂练习
(2)试验的总次数、频数及频率三者的关系是( )
A.频数越大,频率越大
B.频数与总次数成正比
C.总次数一定时,频数越大,频率可达到很大
D.频数一定时,频率与总次数成反比
D
随堂练习
(3)在一副(54张)扑克牌中,摸到“A”的频率是( )
A. B. C. D.无法估计
B
随堂练习
2.(1)在科学课外活动中,小明同学在相同的条件下做了某种作物种子发芽的试验,结果如下表所示:
种子数(个)
100
200
300
400
发芽种子数(个)
94
187
282
376
由此估计这种作物种子的发芽率约为 .(精确到1%)
随堂练习
(2)在一个不透明的袋子中,红色、黑色、白色的玻璃球共有60个,除颜色外,形状、大小、质地等完全相同.小刚通过多次摸球试验后发现其中摸到红色、黑色球的频率稳定在15%和45%,则口袋中白色的球的个数很可能是 个.
3.一组数据有30个,把它们分成四组,其中第一组,第二组的频数分别为7,9,第三组的频率为0.1,则第四组的频数是多少?
解法一:第三组的频数=30×0.1=3,第四组的频数=30-7-3-9=11.
随堂练习
解法二:第一组的频率= ; 第二组的频率= ,
第四组的频率=1-0.1- - = .
第四组的频数= 30× =11.
随堂练习
4.如图,某商场设立了一个可以自由转动的转盘,并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是活动进行中的一组统计数据:
(1)计算并完成表格:
转动转盘的次数n
100
150
200
500
800
1000
落在“铅笔”的次数m
68
111
136
345
564
701
落在“铅笔”的频率
随堂练习
(2)请估计,当n很大时,频率将会接近多少?
(3)假如你去转动转盘一次,你获的铅笔的概率是多少?
解:(1)表格中依次填:0.68,0.74,0.68,0.69,0.705,0.701;
(2)0.7;
(3)0.7;
5.一粒木质中国象棋棋子“兵”,它的正面雕刻一个“兵”字,反面是平的.将它从一定的高度掷下,落地反弹后可能是“兵”字面朝上,也可能是“兵”字面朝下.由于棋子的两面不均匀,因此某试验小组做了棋子下掷试验,试验结果如下表:
试验次数(n)
20
40
60
80
100
120
140
160
“兵”字面朝上的次数(m)
14
38
47
52
66
78
相应的频
率
0.7
0.45
0.59
0.52
0.56
0.55
随堂练习
随堂练习
(1)请将数据表补充完整;
(2)根据上表画出“兵”字面朝上的频率分布折线统计图;
(3)试验继续进行下去,根据上表的数据,这个试验的频率将趋于稳定,这个稳定值是多少?
解:(1)从左向右依次填:18、0.63、0.55、88;
(2)折线图如图所示.
(3)根据表中数据,试验频率分别为0.7、0.45、0.63、0.59、0.52、0.55、0.56、0.55,稳定在0.55左右,故这个稳定值为0.55.
1.频率及其稳定性:
通过试验让学生理解当试验次数较大时,试验的频率具有稳定性,并据此能初步估计出某一事件发生的可能性大小.
2.频率定义:在n次重复试验中,不确定事件A发生了m次,则比值称为事件发生的频率.
课堂小结
再见
6.2 频率的稳定性
第1课时
学习目标
通过掷图钉活动,感受在试验次数很多时,随机事件发生的频率具有稳定性.
理解频率的定义.
抛掷一枚图钉,落地后会
出现两种情况:钉尖朝上 ,
钉尖朝下。你认为钉尖朝上和
钉尖朝下的可能性一样
大吗?
小明和小丽在玩抛图钉游戏
问题情境
直觉告诉我任意掷一枚图钉,钉尖朝上和钉尖朝下的可能性是不相同的.
我的直觉跟你一样,但我不知道对不对.
不妨让我们用试验来验证吧!
问题情境
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}试验总次数
?
钉尖朝上次数
?
钉尖朝下次数
?
钉尖朝上频率(钉尖朝上次数/试验总次数)
?
钉尖朝下频率(钉尖朝下次数/试验总次数)
?
频率定义:在n次重复试验中,不确定事件A发生了m次,则比值 称为事件发生的频率.
探究新知
(1)两人一组做20次掷图钉游戏,并将数据记录在下表中:
(2)累计全班同学的试验结果,并将试验数据汇总填入下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}试验总次数n
20
40
80
120
160
200
240
280
320
360
400
钉尖朝上次数m
?
?
?
?
?
?
?
?
?
?
?
钉尖朝上频率m/n
?
?
?
?
?
?
?
?
?
?
?
探究新知
(3)请同学们根据已填的表格,完成下面的折线统计图
探究新知
20
40
80
120
200
240
160
320
280
0.2
400
360
1.0
0.6
0.8
0.4
钉尖朝上的频率
试验总次数
小明共做了400次掷图钉游戏,并记录了游戏的结果绘制了下面的折线统计图,观察图像,钉尖朝上的频率的变化有什么规律?
探究新知
探究新知
(4)观察图像,钉尖朝上的频率的变化有什么规律?
结论:在试验次数很大时,钉尖朝上的频率都会在一个常数附近摆动,即钉尖朝上的频率具有稳定性
探究新知
议一议:
(1)通过上面的试验,你认为针尖朝上和针尖朝下的可能性一样大吗?你是怎么想的?
(2)小军与小凡一起做了1000次掷图钉的试验,其中有640次针尖朝上,据此,他们认为针尖朝上的可能性比针尖朝下的可能性大,你同意他的说法吗?
人们在长期的实践中发现,在随机试验中,
由于众多微小的偶然因素的影响,每次测
得的结果虽不尽相同,但大量重复试验所
得结果却能反应客观规律.
频率的稳定性是由瑞士数学家雅布·伯努利(1654-1705)最早阐明的,他还提出了由频率可以估计事件发生的可能性大小.
频率稳定性定理
数学史实
典型例题
例1.(1)掷一枚质地均匀的硬币10次,下列说法正确的是 ( )
A.每两次必有1次正面向上 B.可能有5次正面向上
C.必有5次正面向上 D.不可能有10次正面向上
(2)某种彩票的中奖机会是1%,下列说法正确的是 ( )
A.买一张这种彩票一定不会中奖
B.买一张这种彩票一定会中奖
C.买100张这种彩票一定会中奖
D.当购买彩票的数量很大时,中奖的频率稳定在1%
B
D
典型例题
(3)在做图钉落地的试验中,正确的是 ( )
A.甲做了4000次,得出钉尖触地的机会约为46%,于是他断定在做第4001次时,
钉尖肯定不会触地
B.乙认为一次一次做,速度太慢,他拿来了大把材料,形状及大小都完全一样的图钉,随意朝上轻轻抛出,然后统计钉尖触地的次数,这样大大提高了速度
C.老师安排每位同学回家做试验,图钉自由选取
D.老师安排同学回家做试验,图钉统一发(完全一样的图钉).同学交来的结果,老师挑选他满意的进行统计,他不满意的就不要
B
典型例题
(4)一个不透明的盒子里有n个除颜色外其他完全相同的小球,其中有6个黄球.每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后再放回盒子,通过大量重复摸球试验后发现,摸到黄球的频率稳定在30%,那么可以推算出n大约是 ( )
A.6 B.10 C.18 D.20
D
例2.王老师将1个黑球和若干个白球放入一个不透明的口袋并搅匀,让若干学生进行摸球试验,每次摸出一个球(有放回),下表是活动进行中的一组统计数据(结果保留两位小数):
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}摸球的次数n
100
150
200
500
800
1000
摸到黑球的次数m
23
31
60
130
203
251
摸到黑球的频率
0.23
0.21
0.30
0.26
0.25
____
典型例题
(1)补全上表中的有关数据,根据上表数据估计从袋中摸出一个球是黑球的概率是________;
(2)估算袋中白球的个数.
解:(1)251÷1000≈0.25.∵大量重复试验事件发生的频率逐渐稳定到0.25附近,∴估计从袋中摸出一个球是黑球的概率是0.25;
(2)设袋中白球为x个, =0.25,x=3.
答:估计袋中有3个白球.
典型例题
典型例题
例3. 某批篮球质量检验结果如下:
抽取的篮球数n
400
600
800
1000
1200
优等品频数m
376
570
744
940
1128
优等品频率m/n
0.94
____
____
____
____
(1)填写表中优等品的频率;
(2)这批篮球优等品的概率估计值是多少?
典型例题
解:(1) =0.95, =0.93, =0.94, =0.94,
故表中依次填0.95,0.93,0.94,0.94;
(2)这批篮球优等品的概率估计值是0.94.
1.(1)某校男生中,若随机抽取若干名同学做“是否喜欢足球”的问卷调查,抽到喜欢足球的同学的频率是 ,这个 的含义是( ).
A.只发出5份调查卷,其中三份是喜欢足球的答卷
B.在答卷中,喜欢足球的答卷与总问卷的比为3︰8
C.在答卷中,喜欢足球的答卷占总答卷的
D.在答卷中,每抽出100份问卷,恰有60份答卷是喜欢足球
5
3
—
5
3
—
C
5
3
—
随堂练习
随堂练习
(2)试验的总次数、频数及频率三者的关系是( )
A.频数越大,频率越大
B.频数与总次数成正比
C.总次数一定时,频数越大,频率可达到很大
D.频数一定时,频率与总次数成反比
D
随堂练习
(3)在一副(54张)扑克牌中,摸到“A”的频率是( )
A. B. C. D.无法估计
B
随堂练习
2.(1)在科学课外活动中,小明同学在相同的条件下做了某种作物种子发芽的试验,结果如下表所示:
种子数(个)
100
200
300
400
发芽种子数(个)
94
187
282
376
由此估计这种作物种子的发芽率约为 .(精确到1%)
随堂练习
(2)在一个不透明的袋子中,红色、黑色、白色的玻璃球共有60个,除颜色外,形状、大小、质地等完全相同.小刚通过多次摸球试验后发现其中摸到红色、黑色球的频率稳定在15%和45%,则口袋中白色的球的个数很可能是 个.
3.一组数据有30个,把它们分成四组,其中第一组,第二组的频数分别为7,9,第三组的频率为0.1,则第四组的频数是多少?
解法一:第三组的频数=30×0.1=3,第四组的频数=30-7-3-9=11.
随堂练习
解法二:第一组的频率= ; 第二组的频率= ,
第四组的频率=1-0.1- - = .
第四组的频数= 30× =11.
随堂练习
4.如图,某商场设立了一个可以自由转动的转盘,并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是活动进行中的一组统计数据:
(1)计算并完成表格:
转动转盘的次数n
100
150
200
500
800
1000
落在“铅笔”的次数m
68
111
136
345
564
701
落在“铅笔”的频率
随堂练习
(2)请估计,当n很大时,频率将会接近多少?
(3)假如你去转动转盘一次,你获的铅笔的概率是多少?
解:(1)表格中依次填:0.68,0.74,0.68,0.69,0.705,0.701;
(2)0.7;
(3)0.7;
5.一粒木质中国象棋棋子“兵”,它的正面雕刻一个“兵”字,反面是平的.将它从一定的高度掷下,落地反弹后可能是“兵”字面朝上,也可能是“兵”字面朝下.由于棋子的两面不均匀,因此某试验小组做了棋子下掷试验,试验结果如下表:
试验次数(n)
20
40
60
80
100
120
140
160
“兵”字面朝上的次数(m)
14
38
47
52
66
78
相应的频
率
0.7
0.45
0.59
0.52
0.56
0.55
随堂练习
随堂练习
(1)请将数据表补充完整;
(2)根据上表画出“兵”字面朝上的频率分布折线统计图;
(3)试验继续进行下去,根据上表的数据,这个试验的频率将趋于稳定,这个稳定值是多少?
解:(1)从左向右依次填:18、0.63、0.55、88;
(2)折线图如图所示.
(3)根据表中数据,试验频率分别为0.7、0.45、0.63、0.59、0.52、0.55、0.56、0.55,稳定在0.55左右,故这个稳定值为0.55.
1.频率及其稳定性:
通过试验让学生理解当试验次数较大时,试验的频率具有稳定性,并据此能初步估计出某一事件发生的可能性大小.
2.频率定义:在n次重复试验中,不确定事件A发生了m次,则比值称为事件发生的频率.
课堂小结
再见
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
