北师大版七年级数学下册第5章第3节简单的轴对称图形 (2)(共54张PPT)
文档属性
| 名称 | 北师大版七年级数学下册第5章第3节简单的轴对称图形 (2)(共54张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 21:24:13 | ||
图片预览





文档简介
第五章 生活中的轴对称
第1课时 等腰三角形的轴对称性
复习导入
1.如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做 _____.
轴对称图形
这条直线叫做____
对称轴
注:对称轴是一条直线
观察下列各种图形,判断是不是轴对称图形,
能找出对称轴吗?
学习目标
1.掌握等腰三角形的有关概念及性质.
2.了解特殊的等腰三角形(等边三角形)有关概念及性质。
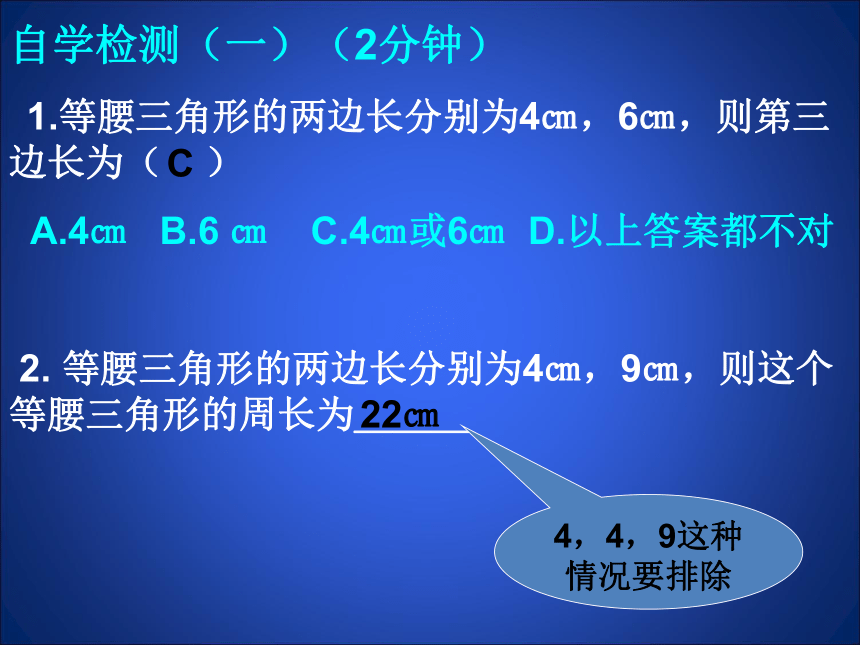
如图:在△ABC中,AB=AC,则 △ABC就是等腰三角形
它的各部分名称分别是什么?
A
B
C
(1)相等的两条边叫做腰。
腰
腰
底边
(2)另一边叫底边。
顶角
底角
底角
(3)两腰的夹角叫顶角。
(4)腰与底边夹角叫底角。
有两条边相等的三角形叫等腰三角形
自学检测(一)(2分钟)
1.等腰三角形的两边长分别为4㎝,6㎝,则第三边长为( )
A.4㎝ B.6 ㎝ C.4㎝或6㎝ D.以上答案都不对
2. 等腰三角形的两边长分别为4㎝,9㎝,则这个等腰三角形的周长为___
22㎝
C
4,4,9这种情况要排除
1.等腰三角形是轴对称图形吗?找出对称轴。
2.顶角的平分线所在的直线是等腰三角形的 对称轴吗?
3.底边上的中线所在的直线是等腰三角形的
对称轴吗?底边上的高所在直线呢?
4.沿对称轴对折,你能发现等腰三角形的哪
些特征?说说你的理由。
思考
等腰三角形是轴对称图形,
请找出它的对称轴;
腰
腰
顶角
底边
底角
底角
(
)
)
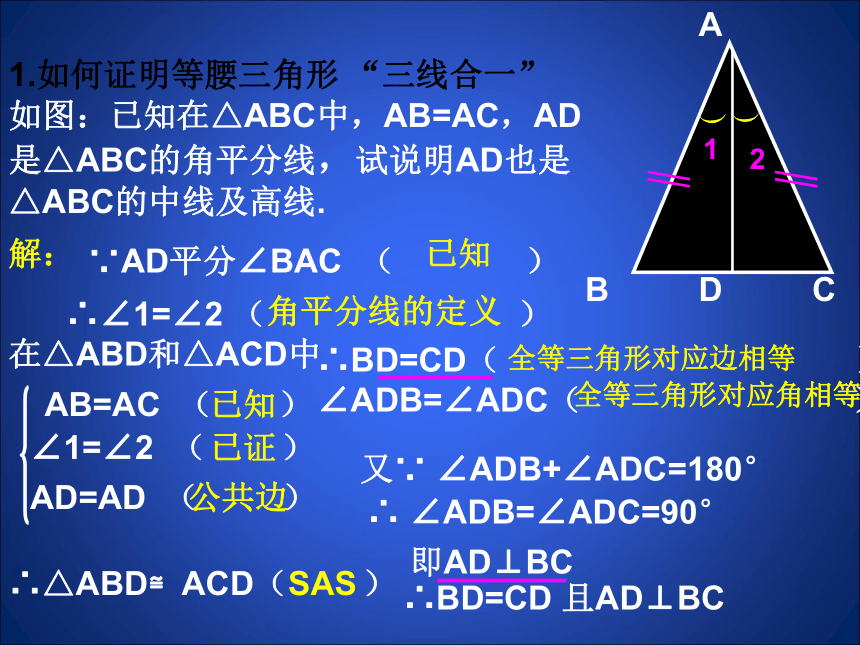
1.如何证明等腰三角形 “三线合一”
如图:已知在△ABC中,AB=AC,AD
是△ABC的角平分线,试说明AD也是
△ABC的中线及高线.
解:
∴∠1=∠2 ( )
A
B
C
D
(
(
1
2
角平分线的定义
已知
在△ABD和△ACD中
AB=AC ( )
∠1=∠2 ( )
AD=AD ( )
∴△ABD≌ACD( )
∴BD=CD( )∠ADB=∠ADC( )
∵AD平分∠BAC ( )
又∵ ∠ADB+∠ADC=180°
∴ ∠ADB=∠ADC=90°
已证
已知
公共边
SAS
即AD⊥BC
∴BD=CD 且AD⊥BC
全等三角形对应边相等
全等三角形对应角相等
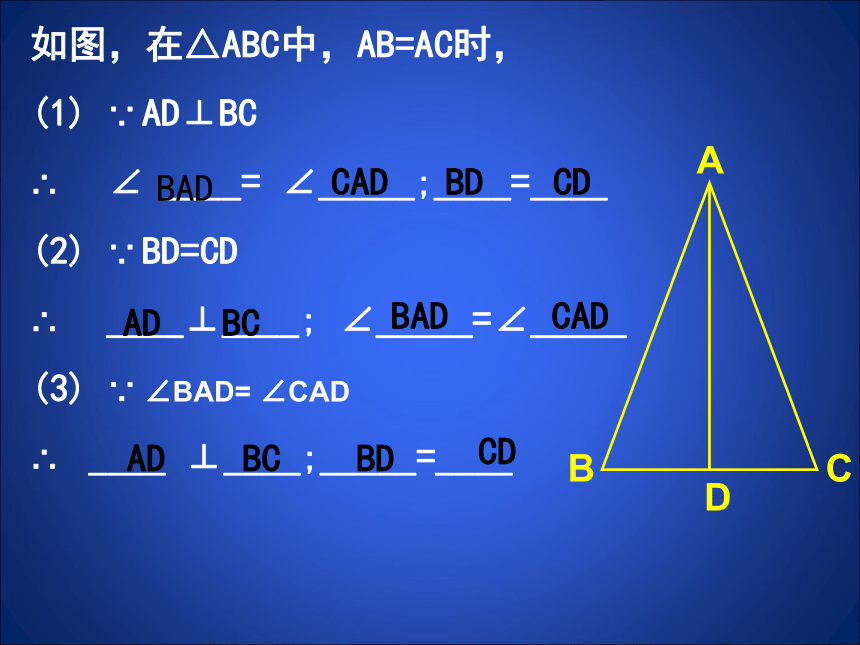
如图,在△ABC中,AB=AC时,
(1) ∵ AD⊥BC
∴ ∠ ____= ∠_____;____=____
(2) ∵ BD=CD
∴ ____⊥____; ∠_____=∠_____
(3) ∵ ∠BAD= ∠CAD
∴ ____ ⊥____;_____=____
BAD
CAD
CD
BD
AD
BC
BAD
CAD
AD
BC
BD
CD
A
B
C
D
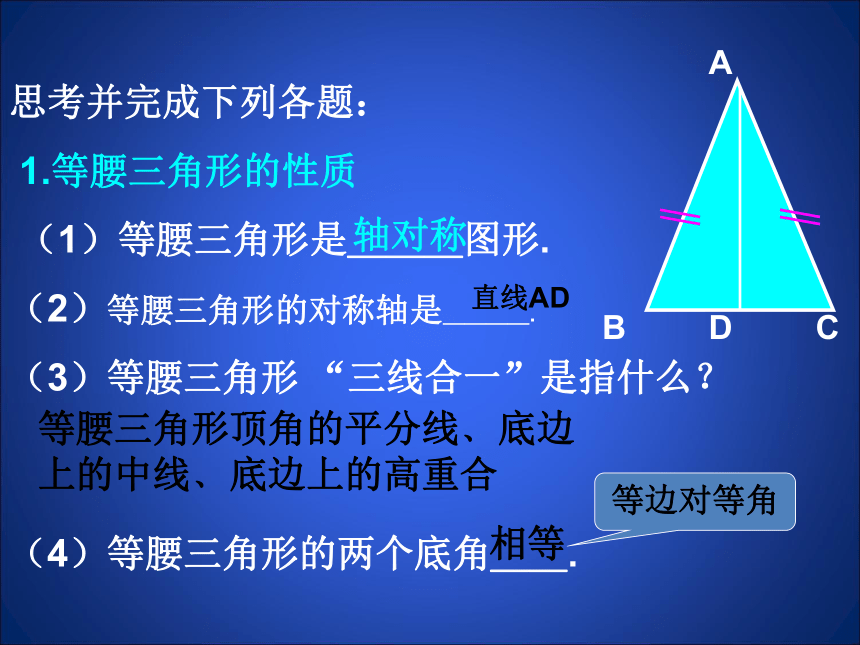
思考并完成下列各题:
1.等腰三角形的性质
(1)等腰三角形是___图形.
(2)等腰三角形的对称轴是____.
(3)等腰三角形 “三线合一”是指什么?
(4)等腰三角形的两个底角__.
轴对称
相等
等腰三角形顶角的平分线﹑底边上的中线﹑底边上的高重合
A
B
C
D
等边对等角
直线AD
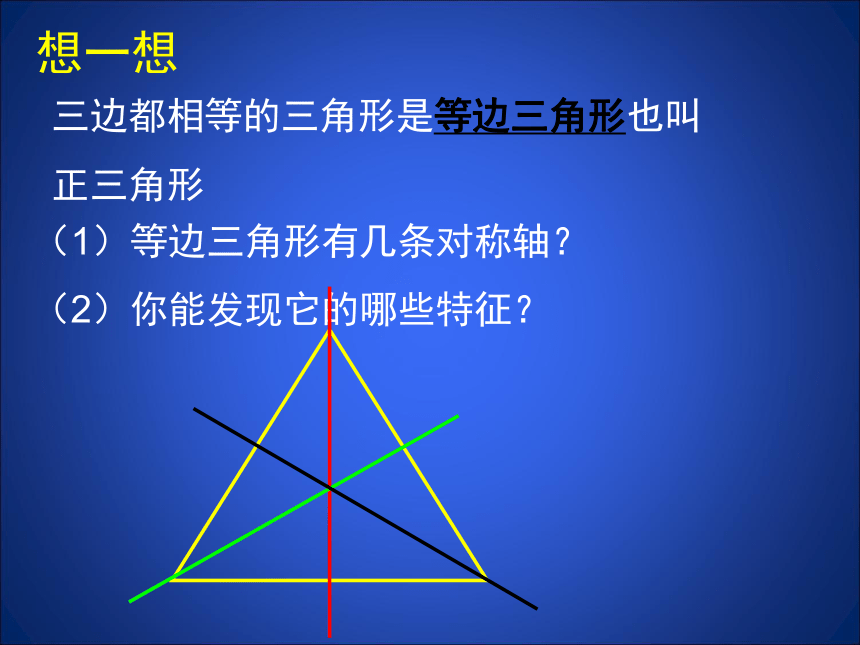
三边都相等的三角形是等边三角形也叫
正三角形
(1)等边三角形有几条对称轴?
(2)你能发现它的哪些特征?
想一想
等边三角形的性质:
1.等边三角形是轴对称图形。
2.等边三角形每个角的平分线和这个角的对 边上的中线、高线重合(“三线合一”),它们所在的直线都是等边三角形的对称轴。等边三角形共有三条对称轴。
3.等边三角形的各角都相等,都等于60°
1.判断:
(1)等腰三角形一角的平分线,一边上的中线 ,一 边上 的高都是它的对称轴. ( )
(2)三角形的高线,角平分线,中线三线合一. ( )
(3)等腰三角形的两底角相等. ( )
(4)有两个内角相等的三角形一定是等腰三角形. ( )
当堂训练
×
×
√
√
如图,是由大小不等的等边三角形组成的图案,请找出它的对称轴。
随堂练习1
如图,在等腰ΔABC中,AB=AC顶角∠A=120°那么底角∠B=_______∠C =_______ .
30°
30°
2. 在△ABC中,AB=AC,∠A=90°,那么
∠B=______
3. 在等腰三角形△ABC中,有一个角为60°,那么另外两个角分别是多少?
B
C
A
45°
随堂练习2
60°
90°
120°
A
B
C
60°
A
B
C
小结
谈谈你的收获吧!
等腰三角形性质:
1.等腰三角形是轴对称图形。
2.等腰三角形顶角的平分线和底边上的中线、高线重合(“三线合一”),它们所在的直线是等边三角形的对称轴。
3.等腰三角形的底角相等。(等边对等角)等边三角形的性质
第五章 生活中的轴对称
第2课时 线段的轴对称性
北师大版 七年级数学下册
基础知识回顾:
1、等腰三角形 、 和 互相重合.
2、如图(1)所示AB=AC BD=5cm,则BC= .
3、已知等腰三角形一个角75度,那么其余两个角的度数为 .
4、一个等腰三角形的周长为35cm,腰长是底边的2倍,则腰长为 ,底边长为 .
5、线段的中点是指: .
6、三角形的重心是指: .
复习
图(1)
下列图形哪些是轴对称图形?
问题1:线段的对称轴是什么?请阅读课本P123
7.线段是轴对称图形吗?如果是,请在图(2)中画出它的对称轴. 你是如何找到线段的对称轴的?
.
8.线段的对称轴与线段存在着什么关系?
.
9.归纳结论:线段是 图形, 是线段的一条对称轴.
10、线段的垂直平分线(简称中垂线)是指:
合作探究
问题2:线段的垂直平分线的性质?
11、课本P123 “议一议” (如图(3),沿OC对折后,AC与BC重合吗?)
(1)如图(3),点C是线段AB的垂直平分线上的一点,AC和BC相等吗?
理由是:
(2)改变点C的位置,以上结论还成立吗?
答:
图(3)
12.归纳线段垂直平分线的性质:
线段垂直平分线上的点_____________________
几何语言:
如图(4)∵OA=OB,OM⊥AB,点C是OM上的一点
∴ AC = BC .
注意:这个结论是经常用来说明两条线段相等的依据之一
问题3:如何用尺规作线段的垂直平分线?
13、课本P124 例 1:利用尺规,作线段AB的垂直平分线
已知:线段AB.
求作:AB的垂直平分线.
作法:1.分别以 和 为圆心,以 的长为半径作弧, 两弧相交于 和 ;
2.作 .
就是线段AB的垂直平分线.
14、为什么第13题这样就能作出线段的垂直平分呢?其中的道理是什么?
15、课本P124 做一做 利用尺规作 △ABC的三边中线
16、利用尺规作△ABC的重心.
练习
1.在△ABC中,BC=10,边BC的垂直平分线分别交AB,BC于点E,D,BE=6,求△BCE的周长.
解:因为DE是线段BC的垂直平分线
所以EC=EB=6
所以△BCE的周长=EB+EC+BC=6+6+10=22
2 如图,AB是△ABC的一条边,DE是AB的垂直平分线,垂足为E,并交BC于点D,已知AB=8cm,BD=6cm,那么EA=________, DA=____.
A
B
E
D
C
(1)
4
6
3、 如图在△ABC中,AB=AC=16cm,AB的垂直平分线交AC于D,如果BC=10cm,那么△BCD的周长是_______cm.
A
B
C
D
E
26
4 如图,已知点D在AB的垂直平分线上,如果
AC=5cm,BC=4cm,那么△BDC的周长是( )cm。
∟
A
D
E
B
C
M
N
9
小结
1. 垂直于一条线段并且平分它的直线叫这条 线段的垂直平分线。
2. 线段是轴对称图形,它的垂直平分线是它的一条对称轴 .
3. 线段垂直平分线上的点到这条线段两个端点的距离相等 .
课外探究:
如图:A,B,C三点表示三个工厂,现要建一供水站,使它到这三个工厂的距离相等,请在图中标出供水站的位置P,请给予说明理由。
A●
B●
c
●
1. 作业本:习题5.4
2. 伴你学:简单的轴对称图形第二课时
作业
5.3 简单的轴对称图形
第3课时 角的轴对称性
A
D
B
C
E
A
D
C
B
不利用工具,请你将一张用纸片做的角分成两个相等的角。你有什么办法?
A
O
B
C
再打开纸片 ,看看折痕与这个角有何关系?
(对折)
C
结论:
角是轴对称图形,角平分线所在的直线是对称轴
A
B
O
有一个简易平分角的仪器(如图),其中AB=AD,BC=DC,将A点放角的顶点,AB和AD沿AC画一条射线AE,AE就是∠BAD的平分线,为什么?
对这种可以折叠的角可以用折叠方法得到角平分线,对不能折叠的角怎样得到其角平分线?
证明:
在△ACD和△ACB中
AD=AB(已知)
DC=BC(已知)
CA=CA(公共边)
∴ △ACD≌ △ACB(SSS)
∴∠CAD=∠CAB(全等三角形的 对应边相等)
∴AC平分∠DAB(角平分线的定义)
A
D
B
C
E
根据角平分仪的制作原理怎样用尺规作一个角的平分线?(不用角平分仪或量角器)
O
A
B
C
E
N
O
M
C
E
N
M
2.分别以M,N为圆心.大于 MN的长为半径作弧.两弧在∠AOB的内部交于C.
用尺规作角的平分线的方法
A
B
O
M
N
C
作法:
1.以O为圆心,适当长为半径作弧,交OA于M,交OB于N.
3.作射线OC.
则射线OC就是∠AOB的平分线.
如图,任意作一个角∠AOB,作出∠AOB的平分线OC.在OC上任取一点P,过点P画出OA,OB的垂线,分别记垂足为D、E,测量PD,PE并作比较,你得到什么结论?在OC上再取几个点试一试.
P
A
O
B
C
D
E
PD=PE
角平分线上的点到这个角的两边的距离相等。
已知:如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别是D,E。
求证:PD=PE
证明:∵ PD⊥OA,PE⊥OB(已知)
∴∠PDO=∠PEO=90(垂直的定义)
在△PDO和△PEO中
∴ PD=PE(全等三角形的对应边相等)
∠ PDO= ∠ PEO ∠ AOC= ∠ BOC OP=OP
∴ △ PDO≌ △ PEO(AAS)
D
P
E
A
O
B
C
角平分线上的点到这个角的两边的距离相等.
角平分线上的点到这个角两边的距离相等。
角平分线的性质:
利用此性质怎样书写推理过程?
一线,一点,
两距离,两相等
角平分线的性质
定理:角平分线上的点到这个角的两边的距离相等。
几何语言
A
O
B
P
E
D
1
2
∵ OP 是∠AOB的平分线
PD ⊥OA ,PE ⊥OB
∴PD=PE
(角的平分线上的点到角的两边的距离相等)
推理的理由有三个,必须写完整,不能少了任何一个。
角平分线的性质
角平分线上的点到这个角的两边的距离相等。
B
A
D
O
P
E
C
定理应用所具备的条件:
(1)角的平分线;
(2)点在该平分线上;
(3)垂直距离。
定理的作用:
证明线段相等。
O
A
B
C
E
D
P
辨一辨
如图,OC平分∠AOB,PD与PE相等吗?
(1)∵ 如图,AD平分∠BAC(已知)
∴ = ,( )
角平分线上的点到这个角的两边的距离相等。
BD CD
(×)
(2)∵ 如图, DC⊥AC,DB⊥AB (已知)
∴ = ,( )
角平分线上的点到这个角的两边的距离相等。
BD CD
(×)
(3)∵ AD平分∠BAC, DC⊥AC,DB⊥AB (已知)
∴ = ,( )
DB
DC
角平分线上的点到这个角的两边的距离相等。
√
不必再证全等
练一练
1、如图, ∵ OC是∠AOB的平分线,
又 ________________
∴PD=PE ( 角的平分线上的点到角的两边的距离相等 )))
PD⊥OA,PE⊥OB
B
O
A
C
D
P
E
2、在Rt△ABC中,BD是角平分线,DE⊥AB,垂足为E,DE与DC相等吗?为什么?
A
B
C
D
E
3、如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别是D、E,PD=4cm,则PE=__________cm.
A
D
O
B
E
P
C
4
4、已知△ABC中, ∠C=900,AD平分∠ CAB,且BC=8,BD=5,求点D到AB的距离是多少?
A
B
C
D
E
你会吗?
5、已知:如图,在△ABC中,AD是它的角平分线且BD=CD∠B=∠C,DE⊥AB, DF⊥AC.垂足分别为E,F.求证:EB=FC.
A
B
C
D
E
F
分析:先利用角平分线的性质定理得到DE=DF,再利用全等证明Rt△BDE ≌ Rt△CDF.
课堂小结
角平分线
尺规作图
属于基本作图,必须熟练掌握
性质定理
一个点:角平分线上的点;
二距离:点到角两边的距离;
两相等:两条垂线段相等
辅助线
添加
过角平分线上一点向两边作垂线段
回味无穷
第1课时 等腰三角形的轴对称性
复习导入
1.如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做 _____.
轴对称图形
这条直线叫做____
对称轴
注:对称轴是一条直线
观察下列各种图形,判断是不是轴对称图形,
能找出对称轴吗?
学习目标
1.掌握等腰三角形的有关概念及性质.
2.了解特殊的等腰三角形(等边三角形)有关概念及性质。
如图:在△ABC中,AB=AC,则 △ABC就是等腰三角形
它的各部分名称分别是什么?
A
B
C
(1)相等的两条边叫做腰。
腰
腰
底边
(2)另一边叫底边。
顶角
底角
底角
(3)两腰的夹角叫顶角。
(4)腰与底边夹角叫底角。
有两条边相等的三角形叫等腰三角形
自学检测(一)(2分钟)
1.等腰三角形的两边长分别为4㎝,6㎝,则第三边长为( )
A.4㎝ B.6 ㎝ C.4㎝或6㎝ D.以上答案都不对
2. 等腰三角形的两边长分别为4㎝,9㎝,则这个等腰三角形的周长为___
22㎝
C
4,4,9这种情况要排除
1.等腰三角形是轴对称图形吗?找出对称轴。
2.顶角的平分线所在的直线是等腰三角形的 对称轴吗?
3.底边上的中线所在的直线是等腰三角形的
对称轴吗?底边上的高所在直线呢?
4.沿对称轴对折,你能发现等腰三角形的哪
些特征?说说你的理由。
思考
等腰三角形是轴对称图形,
请找出它的对称轴;
腰
腰
顶角
底边
底角
底角
(
)
)
1.如何证明等腰三角形 “三线合一”
如图:已知在△ABC中,AB=AC,AD
是△ABC的角平分线,试说明AD也是
△ABC的中线及高线.
解:
∴∠1=∠2 ( )
A
B
C
D
(
(
1
2
角平分线的定义
已知
在△ABD和△ACD中
AB=AC ( )
∠1=∠2 ( )
AD=AD ( )
∴△ABD≌ACD( )
∴BD=CD( )∠ADB=∠ADC( )
∵AD平分∠BAC ( )
又∵ ∠ADB+∠ADC=180°
∴ ∠ADB=∠ADC=90°
已证
已知
公共边
SAS
即AD⊥BC
∴BD=CD 且AD⊥BC
全等三角形对应边相等
全等三角形对应角相等
如图,在△ABC中,AB=AC时,
(1) ∵ AD⊥BC
∴ ∠ ____= ∠_____;____=____
(2) ∵ BD=CD
∴ ____⊥____; ∠_____=∠_____
(3) ∵ ∠BAD= ∠CAD
∴ ____ ⊥____;_____=____
BAD
CAD
CD
BD
AD
BC
BAD
CAD
AD
BC
BD
CD
A
B
C
D
思考并完成下列各题:
1.等腰三角形的性质
(1)等腰三角形是___图形.
(2)等腰三角形的对称轴是____.
(3)等腰三角形 “三线合一”是指什么?
(4)等腰三角形的两个底角__.
轴对称
相等
等腰三角形顶角的平分线﹑底边上的中线﹑底边上的高重合
A
B
C
D
等边对等角
直线AD
三边都相等的三角形是等边三角形也叫
正三角形
(1)等边三角形有几条对称轴?
(2)你能发现它的哪些特征?
想一想
等边三角形的性质:
1.等边三角形是轴对称图形。
2.等边三角形每个角的平分线和这个角的对 边上的中线、高线重合(“三线合一”),它们所在的直线都是等边三角形的对称轴。等边三角形共有三条对称轴。
3.等边三角形的各角都相等,都等于60°
1.判断:
(1)等腰三角形一角的平分线,一边上的中线 ,一 边上 的高都是它的对称轴. ( )
(2)三角形的高线,角平分线,中线三线合一. ( )
(3)等腰三角形的两底角相等. ( )
(4)有两个内角相等的三角形一定是等腰三角形. ( )
当堂训练
×
×
√
√
如图,是由大小不等的等边三角形组成的图案,请找出它的对称轴。
随堂练习1
如图,在等腰ΔABC中,AB=AC顶角∠A=120°那么底角∠B=_______∠C =_______ .
30°
30°
2. 在△ABC中,AB=AC,∠A=90°,那么
∠B=______
3. 在等腰三角形△ABC中,有一个角为60°,那么另外两个角分别是多少?
B
C
A
45°
随堂练习2
60°
90°
120°
A
B
C
60°
A
B
C
小结
谈谈你的收获吧!
等腰三角形性质:
1.等腰三角形是轴对称图形。
2.等腰三角形顶角的平分线和底边上的中线、高线重合(“三线合一”),它们所在的直线是等边三角形的对称轴。
3.等腰三角形的底角相等。(等边对等角)等边三角形的性质
第五章 生活中的轴对称
第2课时 线段的轴对称性
北师大版 七年级数学下册
基础知识回顾:
1、等腰三角形 、 和 互相重合.
2、如图(1)所示AB=AC BD=5cm,则BC= .
3、已知等腰三角形一个角75度,那么其余两个角的度数为 .
4、一个等腰三角形的周长为35cm,腰长是底边的2倍,则腰长为 ,底边长为 .
5、线段的中点是指: .
6、三角形的重心是指: .
复习
图(1)
下列图形哪些是轴对称图形?
问题1:线段的对称轴是什么?请阅读课本P123
7.线段是轴对称图形吗?如果是,请在图(2)中画出它的对称轴. 你是如何找到线段的对称轴的?
.
8.线段的对称轴与线段存在着什么关系?
.
9.归纳结论:线段是 图形, 是线段的一条对称轴.
10、线段的垂直平分线(简称中垂线)是指:
合作探究
问题2:线段的垂直平分线的性质?
11、课本P123 “议一议” (如图(3),沿OC对折后,AC与BC重合吗?)
(1)如图(3),点C是线段AB的垂直平分线上的一点,AC和BC相等吗?
理由是:
(2)改变点C的位置,以上结论还成立吗?
答:
图(3)
12.归纳线段垂直平分线的性质:
线段垂直平分线上的点_____________________
几何语言:
如图(4)∵OA=OB,OM⊥AB,点C是OM上的一点
∴ AC = BC .
注意:这个结论是经常用来说明两条线段相等的依据之一
问题3:如何用尺规作线段的垂直平分线?
13、课本P124 例 1:利用尺规,作线段AB的垂直平分线
已知:线段AB.
求作:AB的垂直平分线.
作法:1.分别以 和 为圆心,以 的长为半径作弧, 两弧相交于 和 ;
2.作 .
就是线段AB的垂直平分线.
14、为什么第13题这样就能作出线段的垂直平分呢?其中的道理是什么?
15、课本P124 做一做 利用尺规作 △ABC的三边中线
16、利用尺规作△ABC的重心.
练习
1.在△ABC中,BC=10,边BC的垂直平分线分别交AB,BC于点E,D,BE=6,求△BCE的周长.
解:因为DE是线段BC的垂直平分线
所以EC=EB=6
所以△BCE的周长=EB+EC+BC=6+6+10=22
2 如图,AB是△ABC的一条边,DE是AB的垂直平分线,垂足为E,并交BC于点D,已知AB=8cm,BD=6cm,那么EA=________, DA=____.
A
B
E
D
C
(1)
4
6
3、 如图在△ABC中,AB=AC=16cm,AB的垂直平分线交AC于D,如果BC=10cm,那么△BCD的周长是_______cm.
A
B
C
D
E
26
4 如图,已知点D在AB的垂直平分线上,如果
AC=5cm,BC=4cm,那么△BDC的周长是( )cm。
∟
A
D
E
B
C
M
N
9
小结
1. 垂直于一条线段并且平分它的直线叫这条 线段的垂直平分线。
2. 线段是轴对称图形,它的垂直平分线是它的一条对称轴 .
3. 线段垂直平分线上的点到这条线段两个端点的距离相等 .
课外探究:
如图:A,B,C三点表示三个工厂,现要建一供水站,使它到这三个工厂的距离相等,请在图中标出供水站的位置P,请给予说明理由。
A●
B●
c
●
1. 作业本:习题5.4
2. 伴你学:简单的轴对称图形第二课时
作业
5.3 简单的轴对称图形
第3课时 角的轴对称性
A
D
B
C
E
A
D
C
B
不利用工具,请你将一张用纸片做的角分成两个相等的角。你有什么办法?
A
O
B
C
再打开纸片 ,看看折痕与这个角有何关系?
(对折)
C
结论:
角是轴对称图形,角平分线所在的直线是对称轴
A
B
O
有一个简易平分角的仪器(如图),其中AB=AD,BC=DC,将A点放角的顶点,AB和AD沿AC画一条射线AE,AE就是∠BAD的平分线,为什么?
对这种可以折叠的角可以用折叠方法得到角平分线,对不能折叠的角怎样得到其角平分线?
证明:
在△ACD和△ACB中
AD=AB(已知)
DC=BC(已知)
CA=CA(公共边)
∴ △ACD≌ △ACB(SSS)
∴∠CAD=∠CAB(全等三角形的 对应边相等)
∴AC平分∠DAB(角平分线的定义)
A
D
B
C
E
根据角平分仪的制作原理怎样用尺规作一个角的平分线?(不用角平分仪或量角器)
O
A
B
C
E
N
O
M
C
E
N
M
2.分别以M,N为圆心.大于 MN的长为半径作弧.两弧在∠AOB的内部交于C.
用尺规作角的平分线的方法
A
B
O
M
N
C
作法:
1.以O为圆心,适当长为半径作弧,交OA于M,交OB于N.
3.作射线OC.
则射线OC就是∠AOB的平分线.
如图,任意作一个角∠AOB,作出∠AOB的平分线OC.在OC上任取一点P,过点P画出OA,OB的垂线,分别记垂足为D、E,测量PD,PE并作比较,你得到什么结论?在OC上再取几个点试一试.
P
A
O
B
C
D
E
PD=PE
角平分线上的点到这个角的两边的距离相等。
已知:如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别是D,E。
求证:PD=PE
证明:∵ PD⊥OA,PE⊥OB(已知)
∴∠PDO=∠PEO=90(垂直的定义)
在△PDO和△PEO中
∴ PD=PE(全等三角形的对应边相等)
∠ PDO= ∠ PEO ∠ AOC= ∠ BOC OP=OP
∴ △ PDO≌ △ PEO(AAS)
D
P
E
A
O
B
C
角平分线上的点到这个角的两边的距离相等.
角平分线上的点到这个角两边的距离相等。
角平分线的性质:
利用此性质怎样书写推理过程?
一线,一点,
两距离,两相等
角平分线的性质
定理:角平分线上的点到这个角的两边的距离相等。
几何语言
A
O
B
P
E
D
1
2
∵ OP 是∠AOB的平分线
PD ⊥OA ,PE ⊥OB
∴PD=PE
(角的平分线上的点到角的两边的距离相等)
推理的理由有三个,必须写完整,不能少了任何一个。
角平分线的性质
角平分线上的点到这个角的两边的距离相等。
B
A
D
O
P
E
C
定理应用所具备的条件:
(1)角的平分线;
(2)点在该平分线上;
(3)垂直距离。
定理的作用:
证明线段相等。
O
A
B
C
E
D
P
辨一辨
如图,OC平分∠AOB,PD与PE相等吗?
(1)∵ 如图,AD平分∠BAC(已知)
∴ = ,( )
角平分线上的点到这个角的两边的距离相等。
BD CD
(×)
(2)∵ 如图, DC⊥AC,DB⊥AB (已知)
∴ = ,( )
角平分线上的点到这个角的两边的距离相等。
BD CD
(×)
(3)∵ AD平分∠BAC, DC⊥AC,DB⊥AB (已知)
∴ = ,( )
DB
DC
角平分线上的点到这个角的两边的距离相等。
√
不必再证全等
练一练
1、如图, ∵ OC是∠AOB的平分线,
又 ________________
∴PD=PE ( 角的平分线上的点到角的两边的距离相等 )))
PD⊥OA,PE⊥OB
B
O
A
C
D
P
E
2、在Rt△ABC中,BD是角平分线,DE⊥AB,垂足为E,DE与DC相等吗?为什么?
A
B
C
D
E
3、如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别是D、E,PD=4cm,则PE=__________cm.
A
D
O
B
E
P
C
4
4、已知△ABC中, ∠C=900,AD平分∠ CAB,且BC=8,BD=5,求点D到AB的距离是多少?
A
B
C
D
E
你会吗?
5、已知:如图,在△ABC中,AD是它的角平分线且BD=CD∠B=∠C,DE⊥AB, DF⊥AC.垂足分别为E,F.求证:EB=FC.
A
B
C
D
E
F
分析:先利用角平分线的性质定理得到DE=DF,再利用全等证明Rt△BDE ≌ Rt△CDF.
课堂小结
角平分线
尺规作图
属于基本作图,必须熟练掌握
性质定理
一个点:角平分线上的点;
二距离:点到角两边的距离;
两相等:两条垂线段相等
辅助线
添加
过角平分线上一点向两边作垂线段
回味无穷
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
