北师大版七年级数学下册第六章6.3.3等可能事件的概率课件(18张PPT)
文档属性
| 名称 | 北师大版七年级数学下册第六章6.3.3等可能事件的概率课件(18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 654.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 23:18:39 | ||
图片预览






文档简介
七年级下册数学第六章6.3.3
等可能事件的概率
一、学习目标
1、在具体情境中进一步了解概率的意义,体会概率是描述不确定现象的数学模型;
2、了解简单几何概率模型发生概率的计算方法,并能进行简单的计算;
3、能设计符合要求的简单概率模型.
二、温故知新
1、10个乒乓球中有8个一等品,2个二等品,从中任取一个是二等品的概率是_____.
2、把标有号码1,2,3,……,10的10个乒乓球放在一个箱子中,摇匀后,从中任意取一个,号码为小于7的奇数的概率是______.
????????
?
????????????
?
三、自主探究:阅读课本p151-152
探究活动1:如何通过面积计算一类事件发生的可能性?
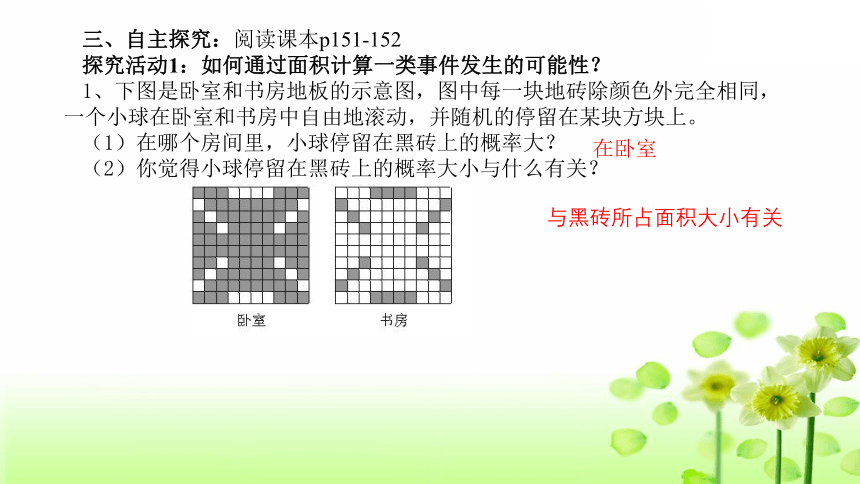
1、下图是卧室和书房地板的示意图,图中每一块地砖除颜色外完全相同,一个小球在卧室和书房中自由地滚动,并随机的停留在某块方块上。
(1)在哪个房间里,小球停留在黑砖上的概率大?
(2)你觉得小球停留在黑砖上的概率大小与什么有关?
在卧室
与黑砖所占面积大小有关
2、假如小球在如图所示的地板上自由地滚动,并随机停留在某块方砖上。回答以下问题并在小组内交流:
(1)题中所说“自由地滚动,并随机停留在某块方砖上”说明了什么?
(2)小球停留在方砖上所有可能出现的结果有几种?停留在黑砖上可能
出现的结果有几种?
(3)小球停留在黑砖上的概率是多少?怎样计算?
(4)小球停留在白砖上的概率是多少?它与停留在黑砖上的概率有何关系?
(5)如果黑砖的面积是5平方米,整个地板的面积是20平方米,小球停留在黑砖的概率多少?
解: (1)说明了小球落在每一块地砖上的可能性是相同的;
(2)小球停留在方砖上所有可能出现的结果有20种,一种是停留在黑砖上,一种是停留在白砖上,停留在黑砖上可能出现的结果有5种。
(3)小球停留在黑砖上的概率是520=14
?
2、假如小球在如上图2所示的地板上自由地滚动,并随机停留在某块方砖上。回答以下问题并在小组内交流:
(1)题中所说“自由地滚动,并随机停留在某块方砖上”说明了什么?
(2)小球停留在方砖上所有可能出现的结果有几种?停留在黑砖上可能
出现的结果有几种?
(3)小球停留在黑砖上的概率是多少?怎样计算?
(4)小球停留在白砖上的概率是多少?它与停留在黑砖上的概率有何关系?
(5)如果黑砖的面积是5平方米,整个地板的面积是20平方米,小球停留在黑砖的概率多少?
(4)小球停留在白砖上的概率是34,
它与停留在黑砖上的概率之和为1
?
(5)小球停留在黑砖的概率520=14
?
3、小明认为在上题中小球最终停留在白砖上的概率与下面事件发生的概率相等:一个袋中装有20个球,其中有5个黑球和15个白球,每个球除颜色外都相同,从中任意摸出一个球是白球。你同意他的想法吗?
同意,因为它们的概率都是34
?
例1 .某商场为了吸引顾客,设立了一个可以自由转动的转盘,并规定:顾客每购买100元的商品,就能获得一次转动转盘的机会。如果转盘停止后,指针正好对准红、黄或绿色区域,顾客就可以获得100元、50元,20元的购物券。(转盘被等分成20个扇形)
甲顾客购物120元,他获得的购物券的概率是多少?他得到100元、50元、20元的购物券的概率分别是多少?
分析:甲顾客购物的钱数在100元到200元之间,可以获得一次转动转盘的机会。
转盘一共等分成20个扇形,其中1份是红色、2份是黄色、4份是绿色,因此,对于该顾客来说,
P(获得购物券)=_____________;P(获得100元购物券)=_____________;
P(获得50元购物券)=________ _;P(获得20元购物券)=_____________。
720
?
120
?
110
?
15
?
例2:如图,A,B是数轴上的两点,在线段AB上任取一点C,则点C到表示-1的点的距离不大于2的概率是 ( )
解:如图,C1与C2到表示-1的点的距离均不大于2,所以C点表示的数在-3和1之间,根据概率公式P=????1????2????????=1?(?3)2?(?3)=45 ?.
故选D.
?
D
四.随堂练习:
1、如图是一个小方块相间的长方形.
(1)用一个小球在上面随意滚动,落在黑色方块(各方块的大小相同)的概率是多少?
(2)小球落在黑色方块的概率大还是落在白色方块的概率大?
(1)落在黑色方块的概率是918=12 ,
(2)一样大
?
2、如图是一个转盘,若转到红色则小明胜,转到黑色则小东胜,这个游戏对双方是否公平?并说明理由.
解:不公平
因为红色的概率是12,黑色的概率是14,所以不公平
?
3、右图的转盘被等分成16个扇形,设计一个游戏,使得自由转动这个转盘,当它停止转动时,指针落在黑色区域的概率为38.
?
4、“十运会”射箭比赛休息之余,一名工作人员发现这样的一幕 :有一只蜘蛛在箭靶上爬来爬去,最终停下来,已知两圆的半径分别是1cm和2cm,内圆为黄色。则P(蜘蛛停留在黄色区域内)= 。
14
?
?????12?????22=14
?
五、小结:
在概率问题中,某些事件的概率与图形的面积的大小有关,这种概率问题称为几何概率.因为几何概率与图形的面积有关,所以只要求出事件A与整个图形面积的__________,就求出了事件A的概率.
比值
六.当堂检测:
1、如图是一个可以自由转动的转盘,当转盘转动停止后,下面有3个表述:
①指针指向3个区域的可能性相同;②指针指向红色区域的概率为13;
③指针指向红色区域的概率为12,其中正确的表述是 (填序号)
?
③
2.如图A、B、C三个可以自由转动的转盘,转盘被等分成若干个扇形,转动转盘,指针停止后,指向白色区域的概率分别是 , , 。
A B C
3. 用扇形统计图反应地球上陆地面积与海洋面积所占比例时,陆地面积所对应的圆心角是108°,当宇宙中一块陨石落在地球上,则落在陆地上的概率是( )
A.0.2 B.0.3 C.0.4 D.0.5
0 23?????????????1
?
B
108360=0.3
?
4.向如图所示的正三角形区域扔沙包(区域中每一个小正三角形除颜色外完全相同),假设沙包击中每一个小三角形是等可能的,扔沙包1次击中阴影区域的概率等于( )
A.16 B. 14 C. 38 D.58
?
C
5.如图,在方格纸中,随机选择标有序号①②③④⑤中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是( )
A. 15 B. 25 C. 35 D. 45
?
解:∵在方格纸中,随机选择标有序号①②③④⑤中的一个小正方形涂黑,共有5种等可能的结果,使与图中阴影部分构成轴对称图形的有②④⑤,3种情况,
∴使与图中阴影部分构成轴对称图形的概率是:35
?
C
等可能事件的概率
一、学习目标
1、在具体情境中进一步了解概率的意义,体会概率是描述不确定现象的数学模型;
2、了解简单几何概率模型发生概率的计算方法,并能进行简单的计算;
3、能设计符合要求的简单概率模型.
二、温故知新
1、10个乒乓球中有8个一等品,2个二等品,从中任取一个是二等品的概率是_____.
2、把标有号码1,2,3,……,10的10个乒乓球放在一个箱子中,摇匀后,从中任意取一个,号码为小于7的奇数的概率是______.
????????
?
????????????
?
三、自主探究:阅读课本p151-152
探究活动1:如何通过面积计算一类事件发生的可能性?
1、下图是卧室和书房地板的示意图,图中每一块地砖除颜色外完全相同,一个小球在卧室和书房中自由地滚动,并随机的停留在某块方块上。
(1)在哪个房间里,小球停留在黑砖上的概率大?
(2)你觉得小球停留在黑砖上的概率大小与什么有关?
在卧室
与黑砖所占面积大小有关
2、假如小球在如图所示的地板上自由地滚动,并随机停留在某块方砖上。回答以下问题并在小组内交流:
(1)题中所说“自由地滚动,并随机停留在某块方砖上”说明了什么?
(2)小球停留在方砖上所有可能出现的结果有几种?停留在黑砖上可能
出现的结果有几种?
(3)小球停留在黑砖上的概率是多少?怎样计算?
(4)小球停留在白砖上的概率是多少?它与停留在黑砖上的概率有何关系?
(5)如果黑砖的面积是5平方米,整个地板的面积是20平方米,小球停留在黑砖的概率多少?
解: (1)说明了小球落在每一块地砖上的可能性是相同的;
(2)小球停留在方砖上所有可能出现的结果有20种,一种是停留在黑砖上,一种是停留在白砖上,停留在黑砖上可能出现的结果有5种。
(3)小球停留在黑砖上的概率是520=14
?
2、假如小球在如上图2所示的地板上自由地滚动,并随机停留在某块方砖上。回答以下问题并在小组内交流:
(1)题中所说“自由地滚动,并随机停留在某块方砖上”说明了什么?
(2)小球停留在方砖上所有可能出现的结果有几种?停留在黑砖上可能
出现的结果有几种?
(3)小球停留在黑砖上的概率是多少?怎样计算?
(4)小球停留在白砖上的概率是多少?它与停留在黑砖上的概率有何关系?
(5)如果黑砖的面积是5平方米,整个地板的面积是20平方米,小球停留在黑砖的概率多少?
(4)小球停留在白砖上的概率是34,
它与停留在黑砖上的概率之和为1
?
(5)小球停留在黑砖的概率520=14
?
3、小明认为在上题中小球最终停留在白砖上的概率与下面事件发生的概率相等:一个袋中装有20个球,其中有5个黑球和15个白球,每个球除颜色外都相同,从中任意摸出一个球是白球。你同意他的想法吗?
同意,因为它们的概率都是34
?
例1 .某商场为了吸引顾客,设立了一个可以自由转动的转盘,并规定:顾客每购买100元的商品,就能获得一次转动转盘的机会。如果转盘停止后,指针正好对准红、黄或绿色区域,顾客就可以获得100元、50元,20元的购物券。(转盘被等分成20个扇形)
甲顾客购物120元,他获得的购物券的概率是多少?他得到100元、50元、20元的购物券的概率分别是多少?
分析:甲顾客购物的钱数在100元到200元之间,可以获得一次转动转盘的机会。
转盘一共等分成20个扇形,其中1份是红色、2份是黄色、4份是绿色,因此,对于该顾客来说,
P(获得购物券)=_____________;P(获得100元购物券)=_____________;
P(获得50元购物券)=________ _;P(获得20元购物券)=_____________。
720
?
120
?
110
?
15
?
例2:如图,A,B是数轴上的两点,在线段AB上任取一点C,则点C到表示-1的点的距离不大于2的概率是 ( )
解:如图,C1与C2到表示-1的点的距离均不大于2,所以C点表示的数在-3和1之间,根据概率公式P=????1????2????????=1?(?3)2?(?3)=45 ?.
故选D.
?
D
四.随堂练习:
1、如图是一个小方块相间的长方形.
(1)用一个小球在上面随意滚动,落在黑色方块(各方块的大小相同)的概率是多少?
(2)小球落在黑色方块的概率大还是落在白色方块的概率大?
(1)落在黑色方块的概率是918=12 ,
(2)一样大
?
2、如图是一个转盘,若转到红色则小明胜,转到黑色则小东胜,这个游戏对双方是否公平?并说明理由.
解:不公平
因为红色的概率是12,黑色的概率是14,所以不公平
?
3、右图的转盘被等分成16个扇形,设计一个游戏,使得自由转动这个转盘,当它停止转动时,指针落在黑色区域的概率为38.
?
4、“十运会”射箭比赛休息之余,一名工作人员发现这样的一幕 :有一只蜘蛛在箭靶上爬来爬去,最终停下来,已知两圆的半径分别是1cm和2cm,内圆为黄色。则P(蜘蛛停留在黄色区域内)= 。
14
?
?????12?????22=14
?
五、小结:
在概率问题中,某些事件的概率与图形的面积的大小有关,这种概率问题称为几何概率.因为几何概率与图形的面积有关,所以只要求出事件A与整个图形面积的__________,就求出了事件A的概率.
比值
六.当堂检测:
1、如图是一个可以自由转动的转盘,当转盘转动停止后,下面有3个表述:
①指针指向3个区域的可能性相同;②指针指向红色区域的概率为13;
③指针指向红色区域的概率为12,其中正确的表述是 (填序号)
?
③
2.如图A、B、C三个可以自由转动的转盘,转盘被等分成若干个扇形,转动转盘,指针停止后,指向白色区域的概率分别是 , , 。
A B C
3. 用扇形统计图反应地球上陆地面积与海洋面积所占比例时,陆地面积所对应的圆心角是108°,当宇宙中一块陨石落在地球上,则落在陆地上的概率是( )
A.0.2 B.0.3 C.0.4 D.0.5
0 23?????????????1
?
B
108360=0.3
?
4.向如图所示的正三角形区域扔沙包(区域中每一个小正三角形除颜色外完全相同),假设沙包击中每一个小三角形是等可能的,扔沙包1次击中阴影区域的概率等于( )
A.16 B. 14 C. 38 D.58
?
C
5.如图,在方格纸中,随机选择标有序号①②③④⑤中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是( )
A. 15 B. 25 C. 35 D. 45
?
解:∵在方格纸中,随机选择标有序号①②③④⑤中的一个小正方形涂黑,共有5种等可能的结果,使与图中阴影部分构成轴对称图形的有②④⑤,3种情况,
∴使与图中阴影部分构成轴对称图形的概率是:35
?
C
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
