北师大版七年级数学下册第六章6.3.4等可能事件的概率课件(共17张))
文档属性
| 名称 | 北师大版七年级数学下册第六章6.3.4等可能事件的概率课件(共17张)) |

|
|
| 格式 | pptx | ||
| 文件大小 | 785.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 00:00:00 | ||
图片预览






文档简介
七年级下册数学第六章6.3.4
等可能事件的概率
一、学习目标
1、了解概率的大小与面积的关系,会进行简单的概率计算;
2、能设计符合要求的简单概率模型,能把不等可能事件转化为等可能事件;
3、会利用扇形圆心角计算概率;
4 、初步认识概率与人类生活的密切联系,感受概率的应用价值。
二、温故知新:
1、密码锁的密码是一个五位数字的号码,每位上的数字都可以是0到9中的任一个,某人忘了密码的最后一位号码,此人开锁时,随意拔动最后一位号码正好开锁的概率是 。
2、如图(1),大圆与小圆的圆心相同,大圆的三条直径把它分成相等的六部分.一只蚂蚁在图案上随意爬动,则蚂蚁恰好停留在阴影部分的概率是 。
110
?
12
?
利用割补法把阴影部分组成半圆
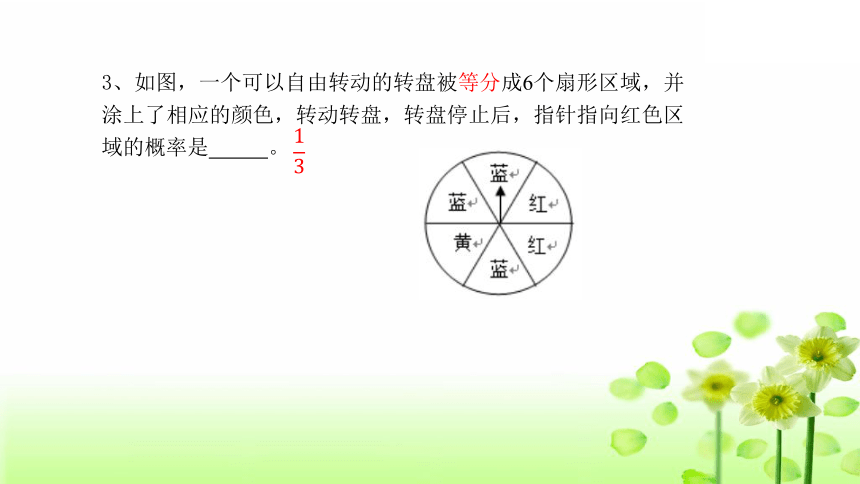
3、如图,一个可以自由转动的转盘被等分成6个扇形区域,并涂上了相应的颜色,转动转盘,转盘停止后,指针指向红色区域的概率是 。
13
?
三、自主探究:阅读课本p154-155
探究活动1:类比等可能的事件,探究可能性不同的事件的概率计算方法
1、如图是一个可以自由转动的转盘,转动转盘,当转盘停止时,指针落在红色区域和白色区域的概率分别是多少?
小明:指针不是落在红色区域就是落在白色区域,落在红色区域和落在白色区域的概率相等,
所以P(落在红色区域)=P(落在白色区域)=12
?
小明的说法正确吗?
小明的说法不正确,因为这不是一个等可能事件,指针落在白色区域的可能性大,我们必须先把它化为的可能事件。
解:如图,把白色的区域分成2等份,这样转盘就被分成3等份,指针落在每一个区域的可能性相等。
P(落在红色区域)=13,P(落在白色区域)=23
?
2、想一想
转动如图所示的转盘,当转盘停止时,指针落在红色区域和白色区域的概率分别是多少?
?
解:P(落在红色区域)=110360=1136
P(落在白色区域)=1-1136=2536
?
1.求可能性不同的事件的概率的方法是:
把可能性不同的事件转化为可能性相同事件;
2.指针指的区域的概率大小只与扇形圆心角的大小有关.
3.所求事件的概率= 。
圆心角360°
?
结论:
例1:某路口南北方向红绿灯的设置时间为:红灯20秒、绿灯60秒、黄灯3秒。小明的爸爸随机地由南往北开车经过该路口,问:
(1)他遇到红灯的概率大还是遇到绿灯的概率大?
(2)他遇到红灯的概率是多少?
解: (1)遇到绿灯的概率大
(2)P(遇到红灯)=2020+60+3=2083
?
例2:“十一”黄金周期间,某购物广场举办迎国庆有奖销售活动,每购物满100元,就会有一次转动答转盘的机会,请你根据大转盘(如图)来计算:
(1)享受七折优惠的概率;
(2)得20元的概率;
(3)得10元的概率;
(4)中奖得钱的概率是多少?
解:(1)享受七折优惠的概率是80360=29
(2)得20元的概率是90360=14
(3)得10元的概率是60+60360=13
(4)中奖得钱的概率是60+90+60+80360=2936
?
指针指的区域的概率=扇形的圆心角????????????°
?
四.随堂练习:
1.在5升水中有一个病毒,现从中随机地取出一升水,含有病毒的概率是多大?
2、如图是一个转盘,小颖认为转盘上共有三种不同的颜色,所以自由转动这个转盘,指针停 在红色、黄色或蓝色区域的概率都是13 ,你认为呢?
?
不对,因为指针这不是一个的可能事件
15
?
P(红色)=12?;??P(黄色)=14; P(蓝色)=14
?
3、如图是一个转盘,扇形1,2,3,4,5所对的圆心角分别是180°,90°,45°,30°,15°,任意转动转盘,求出指针分别指向1,2,3,4,5的概率。(指针恰好指向两扇形交线的概率视为零)。
解:????????=????????????????????????=???????? ;???????????= ????????????????????? = ????????;
?????????= ?????????????????????=???????? ; ????????= ?????????????????????= ???????????? ;
????????= ?????????????????????= ????????????
?
4.如图是芳芳设计的自由转动的转盘,上面写有10个有理数,想想看,转得下列各数的概率是多少?
(1)转得正数;
(2)转得正整数;
(3)转得绝对值小于6的数;
(4)转得绝对值大于8的数.
解: (1)一共有10个有理数,其中正数有5个,所以转得正数的概率是510=12
(2)正整数有4个,所以转得正整数的概率是410=25
(1)绝对值小于6的数有6个,所以转得绝对值小于6的数的概率是610=35
(1)绝对值大于8的数有2个,所以转得绝对值大于8的数的概率是210=15
?
五.当堂检测:
1、小红和小明在操场上做游戏,他们先在地上画了半径为2m和3m的同心圆(如图),蒙上眼睛在一定距离外向圆内扔小石子,投中阴影小红胜,否则小明胜,未扔入圆内不算,请你帮他们计算小红和小明获胜的概率各是多少?
解:小红胜的概率是:?????22?????32=?49;
小明胜的概率是1- 49=59
?
2、一只蚂蚁在如图所示的七巧板上任意爬行,已知它停在这副七巧板上的任一点的可能性相同,求停在各种颜色板上的概率。
解:P1=14 ,P2=14 ,????3=18,
P4=116, ????5=18,
P6=116, ????7=18,
?
3.元旦期间,某超市开展有奖促销活动,凡在超市购物的顾客均有转动圆盘的机会(如图),如果规定当圆盘停下来时指针指向8就中一等奖,指向2或6就中二等奖,指向1或3或5就中纪念奖,指向其余数字不中奖.
(1)转动转盘中奖的概率是多少?
(2)元旦期间有1 000人参与这项活动,估计获得一等奖的人数是多少?
解:(1)因为数字8,2,6,1,3,5的份数之和为6份,
所以转动圆盘中奖的概率为=68=34.
?
(2)根据题意可得,获得一等奖的概率是18,
则元旦这天有1 000人参与这项活动,估计获得一等奖的人数为1 000×18=125(人).
?
4.如图所示的四个转盘中,C,D转盘被分成8等份,若让转盘自由转动一次,停止后,指针落在阴影区域内的概率最大的转盘是( )
A
5.如图,正方形ABCD内的图形来自中国古代的太极图,现随机向正方形内掷一枚小针,则针尖落在黑色区域内的概率为( )
A.14 B. 12 C. ????8 D.????4
?
C
12?????????2(2????)2=????8
等可能事件的概率
一、学习目标
1、了解概率的大小与面积的关系,会进行简单的概率计算;
2、能设计符合要求的简单概率模型,能把不等可能事件转化为等可能事件;
3、会利用扇形圆心角计算概率;
4 、初步认识概率与人类生活的密切联系,感受概率的应用价值。
二、温故知新:
1、密码锁的密码是一个五位数字的号码,每位上的数字都可以是0到9中的任一个,某人忘了密码的最后一位号码,此人开锁时,随意拔动最后一位号码正好开锁的概率是 。
2、如图(1),大圆与小圆的圆心相同,大圆的三条直径把它分成相等的六部分.一只蚂蚁在图案上随意爬动,则蚂蚁恰好停留在阴影部分的概率是 。
110
?
12
?
利用割补法把阴影部分组成半圆
3、如图,一个可以自由转动的转盘被等分成6个扇形区域,并涂上了相应的颜色,转动转盘,转盘停止后,指针指向红色区域的概率是 。
13
?
三、自主探究:阅读课本p154-155
探究活动1:类比等可能的事件,探究可能性不同的事件的概率计算方法
1、如图是一个可以自由转动的转盘,转动转盘,当转盘停止时,指针落在红色区域和白色区域的概率分别是多少?
小明:指针不是落在红色区域就是落在白色区域,落在红色区域和落在白色区域的概率相等,
所以P(落在红色区域)=P(落在白色区域)=12
?
小明的说法正确吗?
小明的说法不正确,因为这不是一个等可能事件,指针落在白色区域的可能性大,我们必须先把它化为的可能事件。
解:如图,把白色的区域分成2等份,这样转盘就被分成3等份,指针落在每一个区域的可能性相等。
P(落在红色区域)=13,P(落在白色区域)=23
?
2、想一想
转动如图所示的转盘,当转盘停止时,指针落在红色区域和白色区域的概率分别是多少?
?
解:P(落在红色区域)=110360=1136
P(落在白色区域)=1-1136=2536
?
1.求可能性不同的事件的概率的方法是:
把可能性不同的事件转化为可能性相同事件;
2.指针指的区域的概率大小只与扇形圆心角的大小有关.
3.所求事件的概率= 。
圆心角360°
?
结论:
例1:某路口南北方向红绿灯的设置时间为:红灯20秒、绿灯60秒、黄灯3秒。小明的爸爸随机地由南往北开车经过该路口,问:
(1)他遇到红灯的概率大还是遇到绿灯的概率大?
(2)他遇到红灯的概率是多少?
解: (1)遇到绿灯的概率大
(2)P(遇到红灯)=2020+60+3=2083
?
例2:“十一”黄金周期间,某购物广场举办迎国庆有奖销售活动,每购物满100元,就会有一次转动答转盘的机会,请你根据大转盘(如图)来计算:
(1)享受七折优惠的概率;
(2)得20元的概率;
(3)得10元的概率;
(4)中奖得钱的概率是多少?
解:(1)享受七折优惠的概率是80360=29
(2)得20元的概率是90360=14
(3)得10元的概率是60+60360=13
(4)中奖得钱的概率是60+90+60+80360=2936
?
指针指的区域的概率=扇形的圆心角????????????°
?
四.随堂练习:
1.在5升水中有一个病毒,现从中随机地取出一升水,含有病毒的概率是多大?
2、如图是一个转盘,小颖认为转盘上共有三种不同的颜色,所以自由转动这个转盘,指针停 在红色、黄色或蓝色区域的概率都是13 ,你认为呢?
?
不对,因为指针这不是一个的可能事件
15
?
P(红色)=12?;??P(黄色)=14; P(蓝色)=14
?
3、如图是一个转盘,扇形1,2,3,4,5所对的圆心角分别是180°,90°,45°,30°,15°,任意转动转盘,求出指针分别指向1,2,3,4,5的概率。(指针恰好指向两扇形交线的概率视为零)。
解:????????=????????????????????????=???????? ;???????????= ????????????????????? = ????????;
?????????= ?????????????????????=???????? ; ????????= ?????????????????????= ???????????? ;
????????= ?????????????????????= ????????????
?
4.如图是芳芳设计的自由转动的转盘,上面写有10个有理数,想想看,转得下列各数的概率是多少?
(1)转得正数;
(2)转得正整数;
(3)转得绝对值小于6的数;
(4)转得绝对值大于8的数.
解: (1)一共有10个有理数,其中正数有5个,所以转得正数的概率是510=12
(2)正整数有4个,所以转得正整数的概率是410=25
(1)绝对值小于6的数有6个,所以转得绝对值小于6的数的概率是610=35
(1)绝对值大于8的数有2个,所以转得绝对值大于8的数的概率是210=15
?
五.当堂检测:
1、小红和小明在操场上做游戏,他们先在地上画了半径为2m和3m的同心圆(如图),蒙上眼睛在一定距离外向圆内扔小石子,投中阴影小红胜,否则小明胜,未扔入圆内不算,请你帮他们计算小红和小明获胜的概率各是多少?
解:小红胜的概率是:?????22?????32=?49;
小明胜的概率是1- 49=59
?
2、一只蚂蚁在如图所示的七巧板上任意爬行,已知它停在这副七巧板上的任一点的可能性相同,求停在各种颜色板上的概率。
解:P1=14 ,P2=14 ,????3=18,
P4=116, ????5=18,
P6=116, ????7=18,
?
3.元旦期间,某超市开展有奖促销活动,凡在超市购物的顾客均有转动圆盘的机会(如图),如果规定当圆盘停下来时指针指向8就中一等奖,指向2或6就中二等奖,指向1或3或5就中纪念奖,指向其余数字不中奖.
(1)转动转盘中奖的概率是多少?
(2)元旦期间有1 000人参与这项活动,估计获得一等奖的人数是多少?
解:(1)因为数字8,2,6,1,3,5的份数之和为6份,
所以转动圆盘中奖的概率为=68=34.
?
(2)根据题意可得,获得一等奖的概率是18,
则元旦这天有1 000人参与这项活动,估计获得一等奖的人数为1 000×18=125(人).
?
4.如图所示的四个转盘中,C,D转盘被分成8等份,若让转盘自由转动一次,停止后,指针落在阴影区域内的概率最大的转盘是( )
A
5.如图,正方形ABCD内的图形来自中国古代的太极图,现随机向正方形内掷一枚小针,则针尖落在黑色区域内的概率为( )
A.14 B. 12 C. ????8 D.????4
?
C
12?????????2(2????)2=????8
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
