北师大版七年级下册数学 6.3等可能事件的概率(第3课时)教学课件 (25张PPT)
文档属性
| 名称 | 北师大版七年级下册数学 6.3等可能事件的概率(第3课时)教学课件 (25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 840.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 21:37:29 | ||
图片预览

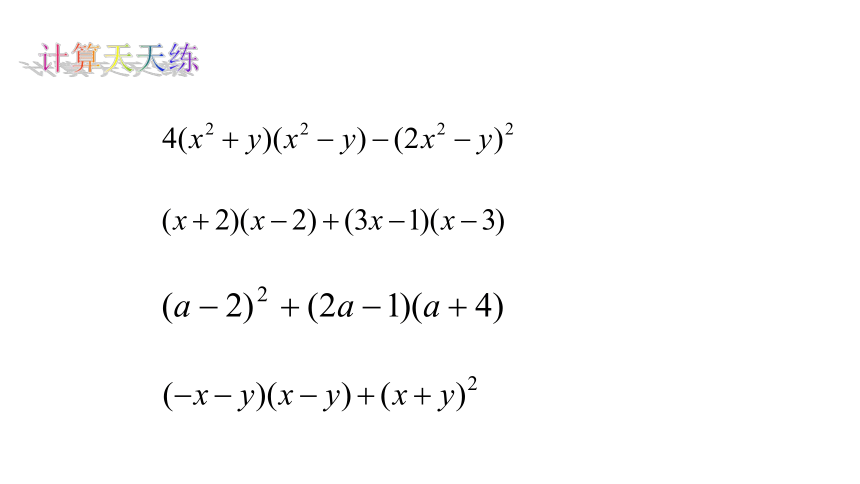
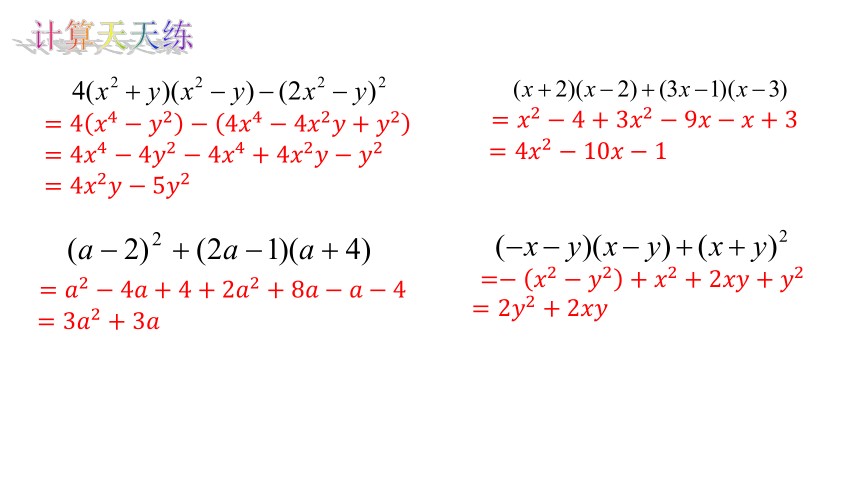




文档简介
城阳初中数学教研
七年级数学
城阳第十五中学 孙香玲
城阳初中数学教研
七年级数学
6.3 等可能事件的概率
第三课时
城阳第十中学 王婧
计算天天练
计算天天练
=4????4?????2?4????4?4????2????+????2
=4????4?4????2?4????4+4????2?????????2
=4????2?????5????2
?
??????????????????????=????2?4+3????2?9?????????+3
=4????2?10?????1
?
???????????????????????????????????????????=????2?4????+4+2????2+8??????????4
=3????2+3????
?
????????????????????????????????????=?????2?????2+????2+2????????+????2
=2????2+2????????
?
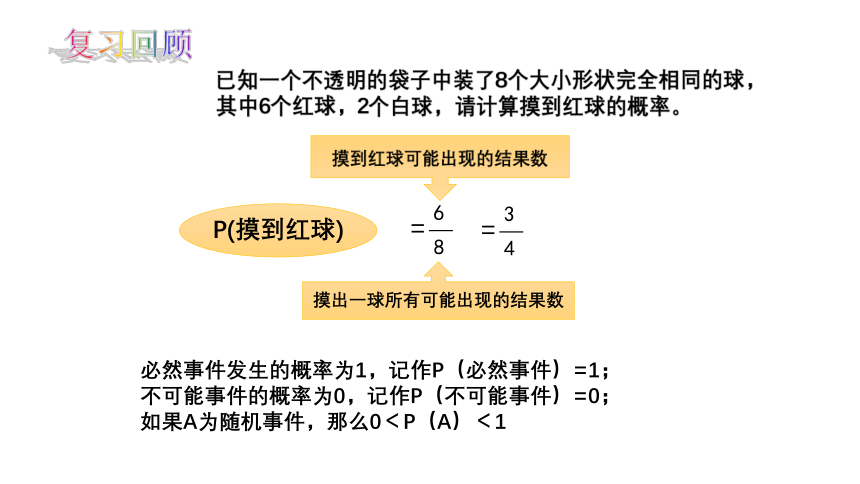
P(摸到红球)
4
3
=
摸出一球所有可能出现的结果数
必然事件发生的概率为1,记作P(必然事件)=1;
不可能事件的概率为0,记作P(不可能事件)=0;
如果A为随机事件,那么0<P(A)<1
复习回顾
已知一个不透明的袋子中装了8个大小形状完全相同的球,其中6个红球,2个白球,请计算摸到红球的概率。
8
6
=
1.了解与面积有关的一类事件发生概率的计算方法,并能进行简单计算;?(重点)
2.能够运用与面积有关的概率解决实际问题.(难点)
学习目标
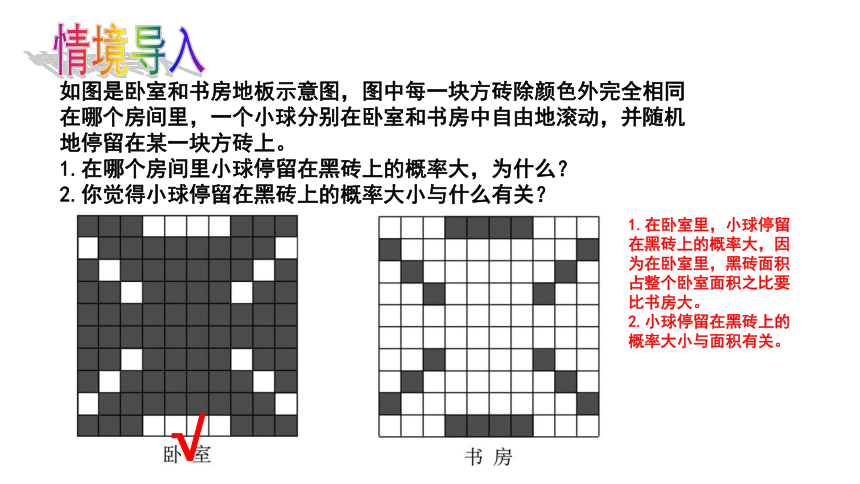
如图是卧室和书房地板示意图,图中每一块方砖除颜色外完全相同在哪个房间里,一个小球分别在卧室和书房中自由地滚动,并随机地停留在某一块方砖上。
1.在哪个房间里小球停留在黑砖上的概率大,为什么?
2.你觉得小球停留在黑砖上的概率大小与什么有关?
情境导入
√
1.在卧室里,小球停留在黑砖上的概率大,因为在卧室里,黑砖面积占整个卧室面积之比要比书房大。
2.小球停留在黑砖上的概率大小与面积有关。
(1)如果小球在如图所示的地板上自由地滚动,并随机停留在某块方砖上,它最终停留在黑砖上的概率是多少?
P(小球最终停在黑砖上)=
5个方砖的面积
20个方砖的面积
20
5
=
探究新知
4
1
=
分析:每一块方砖颜色完全相同,并且小球是随机停留的
(2)小球在如图的地板上自由地滚动,它最
终停留在白色方砖上的概率是多少?
解:P(小球停在白砖上)=
20
15
4
3
=
(3)小明认为(2)中的结果与下面发生的概率相等:袋中装有12个黑球和4个白球,这些球除颜色外都相同,从中任意摸出一球是黑球。你同意吗?
同意,P(摸出一球是黑球)=1212+4=34
?
探究新知
题后反思:1.方砖除颜色不同外,其余完全相同,小球在方砖上滚动方式是随意的,停留在哪一块方砖上是随机的。
2.几何概率的大小与面积有关,即“事件发生的概率等于此事件所有可能发生的结果所组成的图形面积除以所有可能发生的结果所组成的图形面积。”
1.如图,AB、CD是水平放置的轮盘(俯视图)上两条互相垂直的直径,一个小钢球在轮盘上自由滚动,该小钢球最终停在阴影区域的概率为( )
5
1
B.
4
1
A.
8
3
C.
3
2
D.
题后反思: 首先将代数关系用面积表示出来,然后计算所问区域的面积在总面积中占的比例,即为所求的概率。
针对练习
A
2.一位汽车司机准备去商场购物,然后他随意把汽车停在某个停车场内,停车场内一个停车位置正好占一个方格且一个方格除颜色外完全一样,则汽车停在红色区域的概率是
59
?
某商场为了吸引顾客,设立了一个可以自由转动的转盘,并规定:顾客每购买100元的商品,就能获得一次转动转盘的机会。如果转盘停止后,指针正好对准红、黄或绿色区域,顾客就可以获得100元、50元,20元的购物券。(转盘被等分成20个扇形)
甲顾客购物120元,
他获得的购物券的概率
是多少?他得到100元、
50元、20元的购物券的
概率分别是多少?
典型例题
分析:转盘被等分成20个扇形,其中1个是红色,2个是黄色,4个是绿色,对甲顾客来说:
解:
P(获得购物券)=
1+2+4
20
20
7
=
P(获得100元购物券)=
20
1
P(获得50元购物券)=
20
2
P(获得20元购物券)=
20
4
典型例题
10
1
=
5
1
=
题后反思:本题是生活中常见的抽奖促销活动,随机现象就在我们的身边,中奖区域的面积除以总面积,就是我们所求的中奖概率
1.一个可自由转动的圆盘被等分成12块相等的扇形,其中有3块染上了红色,4块染上了绿色,其余都染上了黄色,转盘停止时,指针落在红色区域的概率是 ,落在黄色区域的概率是 , 落在不是绿色区域的概率是
针对练习
2.如图,是自由转动的转盘,被均匀分成10部分,随机转动,则
1.P(指针指向6)= ;
2.P(指针指向奇数)= ;
3.P(指针指向3的倍数)= ;
4.P(指针指向15)= ;
5.P(指针指向的数大于4)= ;
6.P(指针指向的数小于11)= .
3.(培优)某商场举行开业酬宾活动,设立了两个可以自由转动的转盘(如图,两个转盘均被等分)。并规定:顾客购买满188元的商品,即可任选一个转盘转动一次。转盘停止后,指针所指区域内容即为优惠方式。若指针所指区城空白则无优惠,已知小张在该商场消费300元。
(1)若他选择转动转盘1.则他能得到优惠的概率为多少?
(2)选择转动转盘1和转盘2,哪种方式对于小张更合算?请通过计算加以说明.
1.一个可自由转动的圆盘被等分成12块相等的扇形,其中有3块染上了红色,4块染上了绿色,其余都染上了黄色,转盘停止时,指针落在红色区域的概率是 ,落在黄色区域的概率是 , 落在不是绿色区域的概率是 。
针对练习
分析:圆盘被等分成12个相等的扇形,其中3个是红色,4个是绿色,可以求出5个是黄色,需要注意的是第三问,不是绿色的区域指红色和黄色区域。
14
?
512
?
23
?
第三问有两种做法:
法一,已知P(落在绿色区域)=????????????=????????,则????(不落在绿色区域)=?????????????=????????;
法二,已知P(落在红色区域)= ????????????= ????????,P(落在黄色区域)= ????????????,
则P(不落在绿色区域)= ????????+????????????=????????
?
2.如图,是自由转动的转盘,被均匀分成10 部分,随机转动,则
1.P(指针指向6)= ;
2.P(指针指向奇数)= ;
3.P(指针指向3的倍数)= ;
4.P(指针指向15)= ;
5.P(指针指向的数大于4)= ;
6.P(指针指向的数小于11)= .
1
2
3
4
5
6
7
8
9
10
10
1
2
1
10
3
5
3
0
1
针对练习
3.(培优)某商场举行开业酬宾活动,设立了两个可以自由转动的转盘(如图,两个转盘均被等分)。并规定:顾客购买满188元的商品,即可任选一个转盘转动一次。转盘停止后,指针所指区域内容即为优惠方式。若指针所指区域空白则无优惠,已知小张在该商场消费300元。
(1)若他选择转动转盘1.则他能得到优惠的概率为多少?
针对练习
解:
(1)因为整个圆被等分成了12个扇形,其中6个扇形能享受折扣,
所以P(转动转盘1得到优惠)=612=12
?
针对练习
(2)转盘1能获得的优惠为:
300×1?0.7+300×1?0.8×2+300×1?0.9×312
=0.3×300+0.2×300×2+0.1×300×312
=25元,
转盘2能获得的优惠为:
40×24=20元
所以选择转动转盘1更优惠。
?
题后反思:(1)根据转盘1,利用概率公式获得优惠的概率即可;
(2)分别求得转动两个转盘所获得的优惠,然后比较即可得到结论。
(2)选择转动转盘1和转盘2,哪种方式对于小张更合算?请通过计算加以说明.
或者 P(A)=
P(A)=
事件A发生的结果数
所有可能的结果总数
事件A发生的概率表示为
该事件所占区域的面积
总面积
与面积相关的等可能事件概率的计算方法:
课堂小结:
达标检测
1.小球在如图所示的地板上自由滚动,并随机停留在某块正方形的地砖上,则它停在白色地砖上的概率是( )
2.一儿童行走在如图所示的地板上,当他随意停下时,最终停在地板上阴影部分的概率是( )
4. (培优)如图,假设你在每个图形上随机撒一粒黄豆分别计算它落到红色部分的概率.
3.“十运会”射箭比赛休息之余,一名工作人员发现这样的一幕 :有一只蜘蛛在箭靶上爬来爬去,最终停下来,已知两圆的半径分别是1cm和2cm,则P(蜘蛛停留在黄色区域内)=
5.(培优)如图是计算机中“扫雷??游戏的画面.在一个有9X9的方格的正方形雷区中,随机埋藏着10颗地雷,每个方格内最多只能藏1颗地雷.小王在游戏开始时随机地点击一个方格,点击后出现如图所示的情况.我们把与标号3的方格相邻的方格记为A区域(画线部分),A区域外的部分记为B区域.数字3表示在A区域有3颗地雷.下一步应该点击A区域还是B区域?
2.一儿童行走在如图所示的地板上,当他随意停下时,最终停在地板上阴影部分的概率是( )
A
达标检测
1.小球在如图所示的地板上自由滚动,并随机停留在某块正方形的地砖上,则它停在白色地砖上的概率是( )
35
?
3.“十运会”射箭比赛休息之余,一名工作人员发现这样的一幕 :有一只蜘蛛在箭靶上爬来爬去,最终停下来,已知两圆的半径分别是1cm和2cm,则P(蜘蛛停留在黄色区域内)=
达标检测
题后反思:已知圆的面积公式为πr2,将两圆半径分别代入公式,黄色圆的面积除以大圆面积就是蜘蛛停留在黄色区域内的概率
14
?
P=π?12π?22=14
?
4.如图,假设你在每个图形上随机撒一粒黄豆分别计算它落到红色部分的概率.(培优)
解:图①,P=???????? ,
图②,设圆的半径为a,则????=?????????????????????????????????=????????
?
针对练习
题后反思:图1:红色扇形面积与整个圆面积的比;
图2:三角形的面积与圆的面积的比。
5.(培优)如图是计算机中“扫雷??游戏的画面.在一个有9X9的方格的正方形雷区中,随机埋藏着10颗地雷,每个方格内最多只能藏1颗地雷.小王在游戏开始时随机地点击一个方格,点击后出现如图所示的情况.我们把与标号3的方格相邻的方格记为A区域(画线部分),A区域外的部分记为B区域.数字3表示在A区域有3颗地雷.下一步应该点击A区域还是B区域?
达标检测
分析:下一步应该怎样走取决于点击哪部分遇到地雷的概率小,只要分别计算点击两区域内的任一方格遇到地雷的概率并加以比较就可以了.
解:?A区域的方格总共有8个,标号3表示在这8个方格中有3个方格各藏有1颗地雷.因此,点击A区域的任一方格,遇到地雷的概率是????????
?
B区域方格数为9X9-9=72.其中有地雷的方格数为10-3=7.因此,点击B区域的任一方格,遇到地雷的概率是????????????,由于????????>????????????即点击A区域遇到地雷的可能性大于点B区域遇到地雷的可能性,因而第二步应该点击B区域.
?
达标检测
作业:
必做题:
1.课本 第153页 第1、3、题
2.同步 第181-182页第1、2、3、4、6、7、8题
选做题:
同步 第182-183页第9、10、11题
再
见
七年级数学
城阳第十五中学 孙香玲
城阳初中数学教研
七年级数学
6.3 等可能事件的概率
第三课时
城阳第十中学 王婧
计算天天练
计算天天练
=4????4?????2?4????4?4????2????+????2
=4????4?4????2?4????4+4????2?????????2
=4????2?????5????2
?
??????????????????????=????2?4+3????2?9?????????+3
=4????2?10?????1
?
???????????????????????????????????????????=????2?4????+4+2????2+8??????????4
=3????2+3????
?
????????????????????????????????????=?????2?????2+????2+2????????+????2
=2????2+2????????
?
P(摸到红球)
4
3
=
摸出一球所有可能出现的结果数
必然事件发生的概率为1,记作P(必然事件)=1;
不可能事件的概率为0,记作P(不可能事件)=0;
如果A为随机事件,那么0<P(A)<1
复习回顾
已知一个不透明的袋子中装了8个大小形状完全相同的球,其中6个红球,2个白球,请计算摸到红球的概率。
8
6
=
1.了解与面积有关的一类事件发生概率的计算方法,并能进行简单计算;?(重点)
2.能够运用与面积有关的概率解决实际问题.(难点)
学习目标
如图是卧室和书房地板示意图,图中每一块方砖除颜色外完全相同在哪个房间里,一个小球分别在卧室和书房中自由地滚动,并随机地停留在某一块方砖上。
1.在哪个房间里小球停留在黑砖上的概率大,为什么?
2.你觉得小球停留在黑砖上的概率大小与什么有关?
情境导入
√
1.在卧室里,小球停留在黑砖上的概率大,因为在卧室里,黑砖面积占整个卧室面积之比要比书房大。
2.小球停留在黑砖上的概率大小与面积有关。
(1)如果小球在如图所示的地板上自由地滚动,并随机停留在某块方砖上,它最终停留在黑砖上的概率是多少?
P(小球最终停在黑砖上)=
5个方砖的面积
20个方砖的面积
20
5
=
探究新知
4
1
=
分析:每一块方砖颜色完全相同,并且小球是随机停留的
(2)小球在如图的地板上自由地滚动,它最
终停留在白色方砖上的概率是多少?
解:P(小球停在白砖上)=
20
15
4
3
=
(3)小明认为(2)中的结果与下面发生的概率相等:袋中装有12个黑球和4个白球,这些球除颜色外都相同,从中任意摸出一球是黑球。你同意吗?
同意,P(摸出一球是黑球)=1212+4=34
?
探究新知
题后反思:1.方砖除颜色不同外,其余完全相同,小球在方砖上滚动方式是随意的,停留在哪一块方砖上是随机的。
2.几何概率的大小与面积有关,即“事件发生的概率等于此事件所有可能发生的结果所组成的图形面积除以所有可能发生的结果所组成的图形面积。”
1.如图,AB、CD是水平放置的轮盘(俯视图)上两条互相垂直的直径,一个小钢球在轮盘上自由滚动,该小钢球最终停在阴影区域的概率为( )
5
1
B.
4
1
A.
8
3
C.
3
2
D.
题后反思: 首先将代数关系用面积表示出来,然后计算所问区域的面积在总面积中占的比例,即为所求的概率。
针对练习
A
2.一位汽车司机准备去商场购物,然后他随意把汽车停在某个停车场内,停车场内一个停车位置正好占一个方格且一个方格除颜色外完全一样,则汽车停在红色区域的概率是
59
?
某商场为了吸引顾客,设立了一个可以自由转动的转盘,并规定:顾客每购买100元的商品,就能获得一次转动转盘的机会。如果转盘停止后,指针正好对准红、黄或绿色区域,顾客就可以获得100元、50元,20元的购物券。(转盘被等分成20个扇形)
甲顾客购物120元,
他获得的购物券的概率
是多少?他得到100元、
50元、20元的购物券的
概率分别是多少?
典型例题
分析:转盘被等分成20个扇形,其中1个是红色,2个是黄色,4个是绿色,对甲顾客来说:
解:
P(获得购物券)=
1+2+4
20
20
7
=
P(获得100元购物券)=
20
1
P(获得50元购物券)=
20
2
P(获得20元购物券)=
20
4
典型例题
10
1
=
5
1
=
题后反思:本题是生活中常见的抽奖促销活动,随机现象就在我们的身边,中奖区域的面积除以总面积,就是我们所求的中奖概率
1.一个可自由转动的圆盘被等分成12块相等的扇形,其中有3块染上了红色,4块染上了绿色,其余都染上了黄色,转盘停止时,指针落在红色区域的概率是 ,落在黄色区域的概率是 , 落在不是绿色区域的概率是
针对练习
2.如图,是自由转动的转盘,被均匀分成10部分,随机转动,则
1.P(指针指向6)= ;
2.P(指针指向奇数)= ;
3.P(指针指向3的倍数)= ;
4.P(指针指向15)= ;
5.P(指针指向的数大于4)= ;
6.P(指针指向的数小于11)= .
3.(培优)某商场举行开业酬宾活动,设立了两个可以自由转动的转盘(如图,两个转盘均被等分)。并规定:顾客购买满188元的商品,即可任选一个转盘转动一次。转盘停止后,指针所指区域内容即为优惠方式。若指针所指区城空白则无优惠,已知小张在该商场消费300元。
(1)若他选择转动转盘1.则他能得到优惠的概率为多少?
(2)选择转动转盘1和转盘2,哪种方式对于小张更合算?请通过计算加以说明.
1.一个可自由转动的圆盘被等分成12块相等的扇形,其中有3块染上了红色,4块染上了绿色,其余都染上了黄色,转盘停止时,指针落在红色区域的概率是 ,落在黄色区域的概率是 , 落在不是绿色区域的概率是 。
针对练习
分析:圆盘被等分成12个相等的扇形,其中3个是红色,4个是绿色,可以求出5个是黄色,需要注意的是第三问,不是绿色的区域指红色和黄色区域。
14
?
512
?
23
?
第三问有两种做法:
法一,已知P(落在绿色区域)=????????????=????????,则????(不落在绿色区域)=?????????????=????????;
法二,已知P(落在红色区域)= ????????????= ????????,P(落在黄色区域)= ????????????,
则P(不落在绿色区域)= ????????+????????????=????????
?
2.如图,是自由转动的转盘,被均匀分成10 部分,随机转动,则
1.P(指针指向6)= ;
2.P(指针指向奇数)= ;
3.P(指针指向3的倍数)= ;
4.P(指针指向15)= ;
5.P(指针指向的数大于4)= ;
6.P(指针指向的数小于11)= .
1
2
3
4
5
6
7
8
9
10
10
1
2
1
10
3
5
3
0
1
针对练习
3.(培优)某商场举行开业酬宾活动,设立了两个可以自由转动的转盘(如图,两个转盘均被等分)。并规定:顾客购买满188元的商品,即可任选一个转盘转动一次。转盘停止后,指针所指区域内容即为优惠方式。若指针所指区域空白则无优惠,已知小张在该商场消费300元。
(1)若他选择转动转盘1.则他能得到优惠的概率为多少?
针对练习
解:
(1)因为整个圆被等分成了12个扇形,其中6个扇形能享受折扣,
所以P(转动转盘1得到优惠)=612=12
?
针对练习
(2)转盘1能获得的优惠为:
300×1?0.7+300×1?0.8×2+300×1?0.9×312
=0.3×300+0.2×300×2+0.1×300×312
=25元,
转盘2能获得的优惠为:
40×24=20元
所以选择转动转盘1更优惠。
?
题后反思:(1)根据转盘1,利用概率公式获得优惠的概率即可;
(2)分别求得转动两个转盘所获得的优惠,然后比较即可得到结论。
(2)选择转动转盘1和转盘2,哪种方式对于小张更合算?请通过计算加以说明.
或者 P(A)=
P(A)=
事件A发生的结果数
所有可能的结果总数
事件A发生的概率表示为
该事件所占区域的面积
总面积
与面积相关的等可能事件概率的计算方法:
课堂小结:
达标检测
1.小球在如图所示的地板上自由滚动,并随机停留在某块正方形的地砖上,则它停在白色地砖上的概率是( )
2.一儿童行走在如图所示的地板上,当他随意停下时,最终停在地板上阴影部分的概率是( )
4. (培优)如图,假设你在每个图形上随机撒一粒黄豆分别计算它落到红色部分的概率.
3.“十运会”射箭比赛休息之余,一名工作人员发现这样的一幕 :有一只蜘蛛在箭靶上爬来爬去,最终停下来,已知两圆的半径分别是1cm和2cm,则P(蜘蛛停留在黄色区域内)=
5.(培优)如图是计算机中“扫雷??游戏的画面.在一个有9X9的方格的正方形雷区中,随机埋藏着10颗地雷,每个方格内最多只能藏1颗地雷.小王在游戏开始时随机地点击一个方格,点击后出现如图所示的情况.我们把与标号3的方格相邻的方格记为A区域(画线部分),A区域外的部分记为B区域.数字3表示在A区域有3颗地雷.下一步应该点击A区域还是B区域?
2.一儿童行走在如图所示的地板上,当他随意停下时,最终停在地板上阴影部分的概率是( )
A
达标检测
1.小球在如图所示的地板上自由滚动,并随机停留在某块正方形的地砖上,则它停在白色地砖上的概率是( )
35
?
3.“十运会”射箭比赛休息之余,一名工作人员发现这样的一幕 :有一只蜘蛛在箭靶上爬来爬去,最终停下来,已知两圆的半径分别是1cm和2cm,则P(蜘蛛停留在黄色区域内)=
达标检测
题后反思:已知圆的面积公式为πr2,将两圆半径分别代入公式,黄色圆的面积除以大圆面积就是蜘蛛停留在黄色区域内的概率
14
?
P=π?12π?22=14
?
4.如图,假设你在每个图形上随机撒一粒黄豆分别计算它落到红色部分的概率.(培优)
解:图①,P=???????? ,
图②,设圆的半径为a,则????=?????????????????????????????????=????????
?
针对练习
题后反思:图1:红色扇形面积与整个圆面积的比;
图2:三角形的面积与圆的面积的比。
5.(培优)如图是计算机中“扫雷??游戏的画面.在一个有9X9的方格的正方形雷区中,随机埋藏着10颗地雷,每个方格内最多只能藏1颗地雷.小王在游戏开始时随机地点击一个方格,点击后出现如图所示的情况.我们把与标号3的方格相邻的方格记为A区域(画线部分),A区域外的部分记为B区域.数字3表示在A区域有3颗地雷.下一步应该点击A区域还是B区域?
达标检测
分析:下一步应该怎样走取决于点击哪部分遇到地雷的概率小,只要分别计算点击两区域内的任一方格遇到地雷的概率并加以比较就可以了.
解:?A区域的方格总共有8个,标号3表示在这8个方格中有3个方格各藏有1颗地雷.因此,点击A区域的任一方格,遇到地雷的概率是????????
?
B区域方格数为9X9-9=72.其中有地雷的方格数为10-3=7.因此,点击B区域的任一方格,遇到地雷的概率是????????????,由于????????>????????????即点击A区域遇到地雷的可能性大于点B区域遇到地雷的可能性,因而第二步应该点击B区域.
?
达标检测
作业:
必做题:
1.课本 第153页 第1、3、题
2.同步 第181-182页第1、2、3、4、6、7、8题
选做题:
同步 第182-183页第9、10、11题
再
见
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
