北师大版数学八年级下册4.1《因式分解》课件(共18张PPT)
文档属性
| 名称 | 北师大版数学八年级下册4.1《因式分解》课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 670.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 23:26:15 | ||
图片预览






文档简介
因 式 分 解
数学中的游戏
游戏规则:
1.大家说出一个大于1的正整数.
2.写出它的立方减它本身的式子.
如:
3.不通过计算,说出这个式子能被哪些正整数整除.
做一做
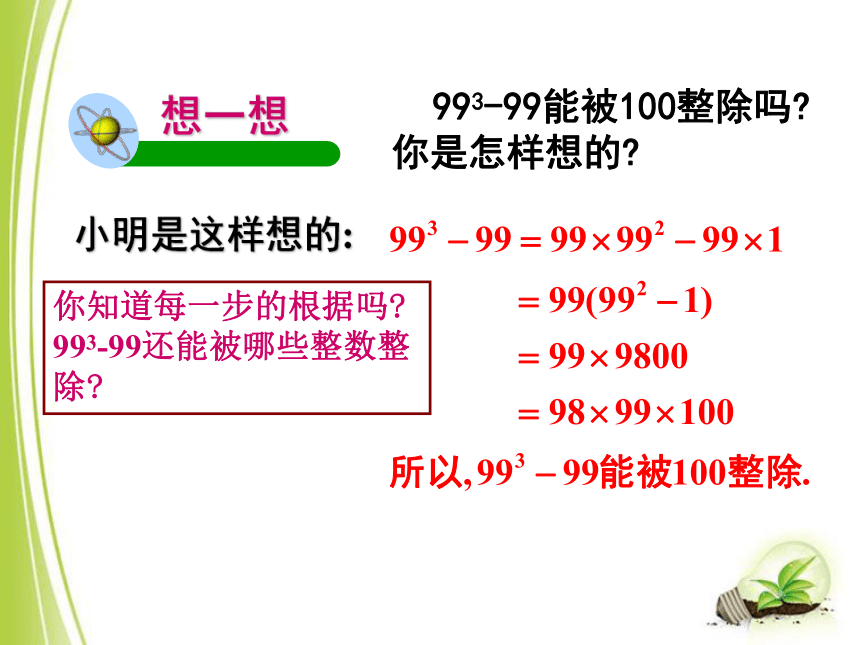
小明是这样想的:
993-99能被100整除吗? 你是怎样想的?
你知道每一步的根据吗?
993-99还能被哪些整数整除?
想一想
1.整式乘法有几种形式?
(1)单项式乘以单项式
(2)单项式乘以多项式
(3)多项式乘以多项式
想一想
回顾 & 思考
a(m+n)= .
(a+b)(m+n)= .
am+an
am+an+bm+bn
(a+b)(a-b)= .
(a±b)2= .
2.乘法公式有哪些?
(1)平方差公式
(2)完全平方公式
想一想
回顾 & 思考
做一做
计算下列各式:
(1) 3x(x-1)= ;
(2)m(a+b+c)= ;
(3) (m+4)(m-4)= ;
(4) ( y-3)2= .
(5)a(a+1)(a-1)= .
根据左面的算式填空:
3x2-3x=( )( )
ma+mb+mc=( )( )
m2-16 =( )( )
y2-6y+9 =( )2
a3-a =( )( )( )
3x2-3x
m2-16
y2-6y+9
ma+mb+mc
a3-a
m
a+b+c
3x
x-1
y-3
m+4
m-4
a
a+1
a-1
由a(a+1)(a-1)得到a3-a的变形是什么运算?
由a3-a得到a(a+1)(a-1)的变形与它有什么不同?
答: 由a(a+1)(a-1)得到a3-a的变形是整式乘法,由a3-a得到a(a+1)(a-1)的变形是把一个多项式化成几个整式的积的形式.
议 一 议
你还能再举一些类似的例子加以说明吗?
因式分解的定义:
把一个多项式化成几个整式的积的形式,这种变形叫做因式分解.因式分解也可称为分解因式.
想一想: 因式分解与整式乘法有什么联系?
理解定义
善于辨析:因式分解与整式乘法有什么联系?
二者是互逆的恒等变形
因式分解
判断下列各式哪些是整式乘法?
哪些是因式分解?
(1) x2-4y2=(x+2y)(x-2y)
(2) 2x(x-3y)=2x2-6xy
(3) (5a-1)2=25a2-10a+1
(4) x2+4x+4=(x+2)2
(5) (a-3)(a+3)=a2-9
因式分解
整式乘法
整式乘法
因式分解
整式乘法
巩固概念
否
是
否
否
是
否
下列式子从左到右的变形是否为因式分解?为什么?
巩固概念
(1)因式分解与整式的乘法是一种互逆关系;
(2)因式分解的对象必须是多项式,结果要以积的形式表示;
(3)分解后的每个因式必须是整式,次数都低于原来的多项式的次数;
归纳
(4)必须分解到每个因式不能再分解为止.
x2-y2
(3-5x)(3+5x)
(x+1)2
xy-y2
x2+2x+1
y(x-y)
9-25x2
(x-y)(x+y)
随堂练习
把左右两边对应的式子连起来,并说明哪些变形是因式分解,哪些是整式乘法.
1. 计算: 7652×17-2352 ×17
解: 7652×17-2352 ×17
= 17(7652 -2352)
= 17(765+235)(765 -235)
= 17×1000×530
= 9010000
随堂练习
拓展应用
2. 20042+2004能被2005整除吗?
解: ∵20042+2004
=2004(2004+1)
=2004×2005
∴ 20042+2004能被2005整除
随堂练习
拓展应用
假如用一根比地球赤道长10米的铁丝将地球赤道围起来, 那么铁丝与赤道之间均匀的间隙能有多大(赤道看成圆形,设地球的半径为r,铁丝围成圆形的半径为R)?
随堂练习
拓展应用
R–r
所以,铁丝与赤道之间均匀的间隙为 米.
解:根据题意可得,
本节小结
2. 分解因式与整式乘法是互逆过程;
1. 把一个多项式化成几个整式乘积的形式,这种变形叫做把这个多项式分解因式;
3. 分解因式的结果要以积的形式表示;
4. 分解后的每个因式必须是整式,次数都低于原来的多项式的次数;
5. 必须分解到每个多项式不能再分解为止.
6. 分解因式在实际问题中的应用.
数学中的游戏
游戏规则:
1.大家说出一个大于1的正整数.
2.写出它的立方减它本身的式子.
如:
3.不通过计算,说出这个式子能被哪些正整数整除.
做一做
小明是这样想的:
993-99能被100整除吗? 你是怎样想的?
你知道每一步的根据吗?
993-99还能被哪些整数整除?
想一想
1.整式乘法有几种形式?
(1)单项式乘以单项式
(2)单项式乘以多项式
(3)多项式乘以多项式
想一想
回顾 & 思考
a(m+n)= .
(a+b)(m+n)= .
am+an
am+an+bm+bn
(a+b)(a-b)= .
(a±b)2= .
2.乘法公式有哪些?
(1)平方差公式
(2)完全平方公式
想一想
回顾 & 思考
做一做
计算下列各式:
(1) 3x(x-1)= ;
(2)m(a+b+c)= ;
(3) (m+4)(m-4)= ;
(4) ( y-3)2= .
(5)a(a+1)(a-1)= .
根据左面的算式填空:
3x2-3x=( )( )
ma+mb+mc=( )( )
m2-16 =( )( )
y2-6y+9 =( )2
a3-a =( )( )( )
3x2-3x
m2-16
y2-6y+9
ma+mb+mc
a3-a
m
a+b+c
3x
x-1
y-3
m+4
m-4
a
a+1
a-1
由a(a+1)(a-1)得到a3-a的变形是什么运算?
由a3-a得到a(a+1)(a-1)的变形与它有什么不同?
答: 由a(a+1)(a-1)得到a3-a的变形是整式乘法,由a3-a得到a(a+1)(a-1)的变形是把一个多项式化成几个整式的积的形式.
议 一 议
你还能再举一些类似的例子加以说明吗?
因式分解的定义:
把一个多项式化成几个整式的积的形式,这种变形叫做因式分解.因式分解也可称为分解因式.
想一想: 因式分解与整式乘法有什么联系?
理解定义
善于辨析:因式分解与整式乘法有什么联系?
二者是互逆的恒等变形
因式分解
判断下列各式哪些是整式乘法?
哪些是因式分解?
(1) x2-4y2=(x+2y)(x-2y)
(2) 2x(x-3y)=2x2-6xy
(3) (5a-1)2=25a2-10a+1
(4) x2+4x+4=(x+2)2
(5) (a-3)(a+3)=a2-9
因式分解
整式乘法
整式乘法
因式分解
整式乘法
巩固概念
否
是
否
否
是
否
下列式子从左到右的变形是否为因式分解?为什么?
巩固概念
(1)因式分解与整式的乘法是一种互逆关系;
(2)因式分解的对象必须是多项式,结果要以积的形式表示;
(3)分解后的每个因式必须是整式,次数都低于原来的多项式的次数;
归纳
(4)必须分解到每个因式不能再分解为止.
x2-y2
(3-5x)(3+5x)
(x+1)2
xy-y2
x2+2x+1
y(x-y)
9-25x2
(x-y)(x+y)
随堂练习
把左右两边对应的式子连起来,并说明哪些变形是因式分解,哪些是整式乘法.
1. 计算: 7652×17-2352 ×17
解: 7652×17-2352 ×17
= 17(7652 -2352)
= 17(765+235)(765 -235)
= 17×1000×530
= 9010000
随堂练习
拓展应用
2. 20042+2004能被2005整除吗?
解: ∵20042+2004
=2004(2004+1)
=2004×2005
∴ 20042+2004能被2005整除
随堂练习
拓展应用
假如用一根比地球赤道长10米的铁丝将地球赤道围起来, 那么铁丝与赤道之间均匀的间隙能有多大(赤道看成圆形,设地球的半径为r,铁丝围成圆形的半径为R)?
随堂练习
拓展应用
R–r
所以,铁丝与赤道之间均匀的间隙为 米.
解:根据题意可得,
本节小结
2. 分解因式与整式乘法是互逆过程;
1. 把一个多项式化成几个整式乘积的形式,这种变形叫做把这个多项式分解因式;
3. 分解因式的结果要以积的形式表示;
4. 分解后的每个因式必须是整式,次数都低于原来的多项式的次数;
5. 必须分解到每个多项式不能再分解为止.
6. 分解因式在实际问题中的应用.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
