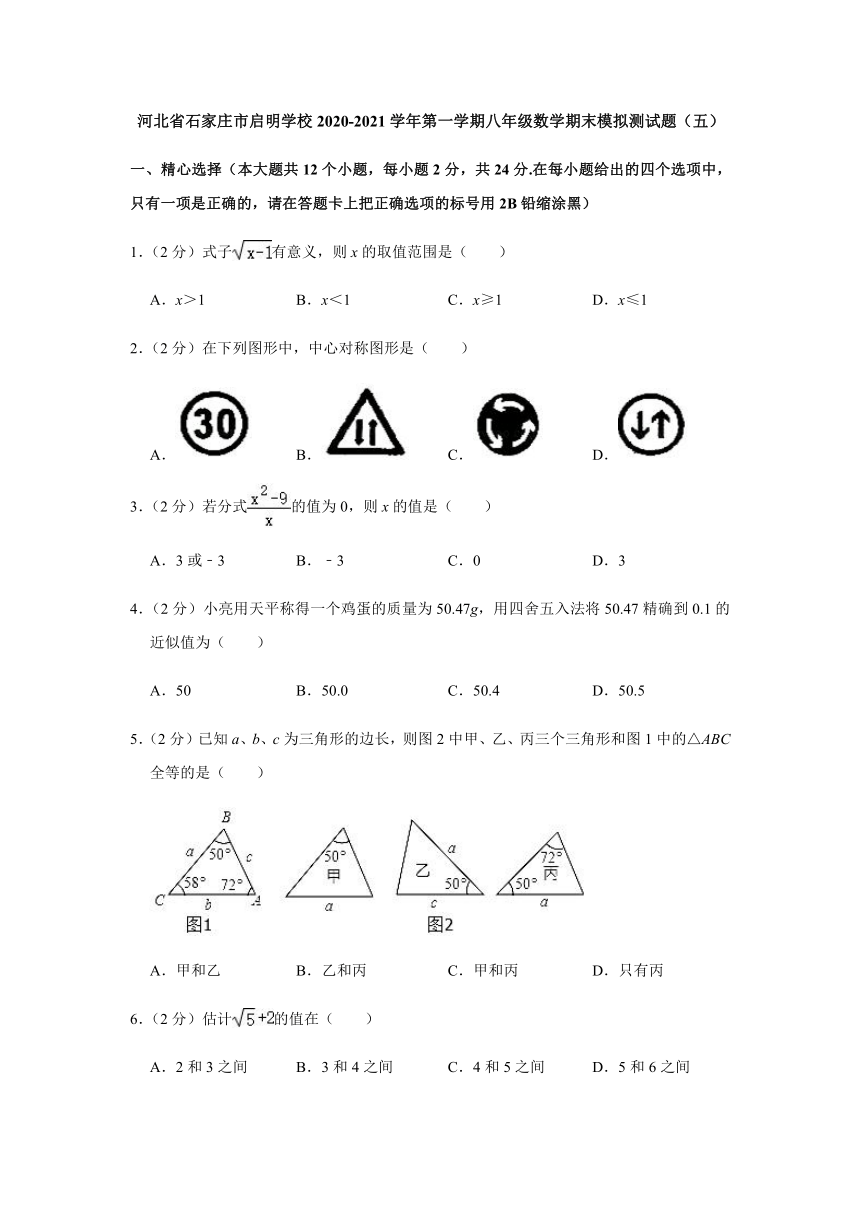
河北省石家庄市启明学校2020-2021学年第一学期八年级数学期末模拟测试题(五)(Word版,附答案解析)
文档属性
| 名称 | 河北省石家庄市启明学校2020-2021学年第一学期八年级数学期末模拟测试题(五)(Word版,附答案解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 487.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 00:00:00 | ||
图片预览





文档简介
河北省石家庄市启明学校2020-2021学年第一学期八年级数学期末模拟测试题(五)
一、精心选择(本大题共12个小题,每小题2分,共24分.在每小题给出的四个选项中,只有一项是正确的,请在答题卡上把正确选项的标号用2B铅缩涂黑)
1.(2分)式子有意义,则x的取值范围是( )
A.x>1
B.x<1
C.x≥1
D.x≤1
2.(2分)在下列图形中,中心对称图形是( )
A.
B.
C.
D.
3.(2分)若分式的值为0,则x的值是( )
A.3或﹣3
B.﹣3
C.0
D.3
4.(2分)小亮用天平称得一个鸡蛋的质量为50.47g,用四舍五入法将50.47精确到0.1的近似值为( )
A.50
B.50.0
C.50.4
D.50.5
5.(2分)已知a、b、c为三角形的边长,则图2中甲、乙、丙三个三角形和图1中的△ABC全等的是( )
A.甲和乙
B.乙和丙
C.甲和丙
D.只有丙
6.(2分)估计的值在( )
A.2和3之间
B.3和4之间
C.4和5之间
D.5和6之间
7.(2分)如图,在△ABC中,AB=AC,AD、CE分别是△ABC的中线和角平分线,当∠ACE=35°时,∠BAD的度数是( )
A.55°
B.40°
C.35°
D.20°
8.(2分)下列等式正确的是( )
A.
B.
C.
D.
9.(2分)在用反证法证明“三角形的最大内角不小于60°”时,假设三角形的最大内角不小于60°不成立,则有三角形的最大内角( )
A.小于60°
B.等于60°
C.大于60°
D.大于或等于60°
10.(2分)=( )
A.
B.
C.
D.
11.(2分)如图,在△ABC中,DE是AC的垂直平分线,且分别交BC、AC于D、E两点,∠B=60°,∠BAD=70°,则∠BAC的度数为( )
A.130°
B.95°
C.90°
D.85°
12.(2分)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,BF平分∠ABC,交CD于点E,交AC于点F.若AB=10,BC=6,则CE的长为( )
A.3
B.4
C.5
D.6
二、准确填空(本大题共6个小题,每小题3分,共18分.请你把答案写在横线上)
13.(3分)8的立方根是
.
14.(3分)如图所示的五角星是轴对称图形,它的对称轴共有
条.
15.(3分)计算:=
.
16.(3分)如图,OC为∠AOB的平分线,CM⊥OB,OC=5,OM=4,则点C到射线OA的距离为
.
17.(3分)若关于x的分式方程有增根,则m的值为
.
18.(3分)如图,△ACB和△DCE都是等腰直角三角形,AC=BC,DC=EC,△ACB的顶点A在△DCE的斜边DE上,若AD=,AE=,则BC=
.
三、挑战技能(本大题共4个小题,每小题6分,共24分)
19.(6分)计算:
20.(6分)已知:如图,∠A=∠D=90°,AC=DB,AC、DB相交于点O.
求证:△OBC是等腰三角形.
21.(6分)顶点都在格点上的三角形叫做格点三角形,如图,在4×4的方格纸中,△ABC是格点三角形.
(1)在图1中,以点C为对称中心,作出一个与△ABC成中心对称的格点三角形DEC,在题后横线上直接写出AB与DE的位置关系:
;
(2)在图2中,以AC所在的直线为对称轴,作出一个与△ABC成轴对称的格点三角形AFC,并在后横线上直接写出△BCF是什么形状的特殊三角形:
.
22.(6分)当x﹣y=2时,求的值.
第二部分实践与应用
23.(8分)《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,来折抵地,去本三尺,问折者高几何?“译成数学问题是:如图所示,在△ABC中,∠ACB=90°,AC+AB=1丈,BC=3尺,求AC的长为多少尺?(说明:1丈=10尺)
24.(8分)观察下列各式:
请利用你所发现的规律,解决下列问题:
(1)第4个算式为:
;
(2)求的值;
(3)诸直接写出的结果.
25.(9分)已知:如图1,OM是∠AOB的平分线,点C在OM上,OC=5,且点C到OA的距离为3.过点C作CD⊥OA,CE⊥OB,垂足分别为D、E,易得到结论:OD+OE=
;
(1)把图1中的∠DCE绕点C旋转,当CD与OA不垂直时(如图2),上述结论是否成立?并说明理由;
(2)把图1中的∠DCE绕点C旋转,当CD与OA的反向延长线相交于点D时:
①请在图3中画出图形;
②上述结论还成立吗?若成立,请给出证明;若不成立,请直接写出线段OD、OE之间的数量关系,不需证明.
26.(9分)如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,E为AB边的中点,以BE为边作等边△BDE,连接AD、CD.
(1)求证:AD=CD;
(2)①画图:在AC边上找一点H,使得BH+EH最小(要求:写出作图过程并画出图形,不用说明作图依据);
②当BC=2时,求出BH+EH的最小值.
参考答案与试题解析
一、精心选择(本大题共12个小题,每小题2分,共24分.在每小题给出的四个选项中,只有一项是正确的,请在答题卡上把正确选项的标号用2B铅缩涂黑)
1.(2分)式子有意义,则x的取值范围是( )
A.x>1
B.x<1
C.x≥1
D.x≤1
【分析】根据二次根式的被开方数是非负数列出不等式x﹣1≥0,通过解该不等式即可求得x的取值范围.
【解答】解:根据题意,得x﹣1≥0,
解得,x≥1.
故选:C.
2.(2分)在下列图形中,中心对称图形是( )
A.
B.
C.
D.
【分析】根据中心对称图形的概念求解.
【解答】解:A.不是中心对称图形,故此选项错误;
B.不是中心对称图形,故此选项错误;
C.不是中心对称图形,故此选项错误;
D.是中心对称图形,故此选项正确;
故选:D.
3.(2分)若分式的值为0,则x的值是( )
A.3或﹣3
B.﹣3
C.0
D.3
【分析】根据分式的值为零的条件可以求出x的值.
【解答】解:依题意得:x2﹣9=0且x≠0,
解得x=±3.
故选:A.
4.(2分)小亮用天平称得一个鸡蛋的质量为50.47g,用四舍五入法将50.47精确到0.1的近似值为( )
A.50
B.50.0
C.50.4
D.50.5
【分析】根据四舍五入法可以解答本题.
【解答】解:50.47≈50.5(精确到0.1),
故选:D.
5.(2分)已知a、b、c为三角形的边长,则图2中甲、乙、丙三个三角形和图1中的△ABC全等的是( )
A.甲和乙
B.乙和丙
C.甲和丙
D.只有丙
【分析】首先观察图形,然后根据三角形全等的判定方法(AAS与SAS),即可求得答案.
【解答】解:如图:
在△ABC和△MNK中,,
∴△ABC≌△NKM(SAS);
在△ABC和△HIG中,,
∴△ABC≌△GHI(AAS).
∴甲、乙、丙三个三角形中和△ABC全等的图形是:乙和丙.
故选:B.
6.(2分)估计的值在( )
A.2和3之间
B.3和4之间
C.4和5之间
D.5和6之间
【分析】直接得出的取值范围进而得出答案.
【解答】解:∵,
∴,
故选:C.
7.(2分)如图,在△ABC中,AB=AC,AD、CE分别是△ABC的中线和角平分线,当∠ACE=35°时,∠BAD的度数是( )
A.55°
B.40°
C.35°
D.20°
【分析】根据角平分线的定义和等腰三角形的性质即可得到结论.
【解答】解:∵CE是∠ACB的平分线,∠ACE=35°,
∴∠ACB=2∠ACE=70°,
∵AB=AC,
∴∠B=∠ACB=70°,
∵AD⊥BC,
∴∠ADB=90°,
∴∠BAD=90°﹣∠B=20°,
故选:D.
8.(2分)下列等式正确的是( )
A.
B.
C.
D.
【分析】根据二次根式的性质1和性质2逐一判断即可得.
【解答】解:A.=2,故本选项不符合题意;
B.()2=2,故本选项符合题意;
C.﹣=﹣2,故本选项不符合题意;
D.(﹣)2=2,故本选项不符合题意;
故选:B.
9.(2分)在用反证法证明“三角形的最大内角不小于60°”时,假设三角形的最大内角不小于60°不成立,则有三角形的最大内角( )
A.小于60°
B.等于60°
C.大于60°
D.大于或等于60°
【分析】根据反证法的步骤,从命题的反面出发假设出结论.
【解答】解:在用反证法证明“三角形的最大内角不小于60°”时,
假设三角形的最大内角不小于60°不成立,则有三角形的最大内角小于60°.
故选:A.
10.(2分)=( )
A.
B.
C.
D.
【分析】根据二次根式的性质4化简可得.
【解答】解:===,
故选:D.
11.(2分)如图,在△ABC中,DE是AC的垂直平分线,且分别交BC、AC于D、E两点,∠B=60°,∠BAD=70°,则∠BAC的度数为( )
A.130°
B.95°
C.90°
D.85°
【分析】根据线段垂直平分线的性质得到DA=DC,根据等腰三角形的性质得到∠DAC=∠C,根据三角形内角和定理求出∠BDA的度数,计算出结果.
【解答】解:∵DE是AC的垂直平分线,
∴DA=DC,
∴∠DAC=∠C,
∵∠B=60°,∠BAD=70°,
∴∠BDA=50°,
∴∠DAC=∠BDA=25°,
∴∠BAC=∠BAD+∠DAC=70°+25°=95°
故选:B.
12.(2分)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,BF平分∠ABC,交CD于点E,交AC于点F.若AB=10,BC=6,则CE的长为( )
A.3
B.4
C.5
D.6
【分析】根据三角形的内角和定理得出∠CBF+∠CFB=90°,∠FBD+∠BED=90°,根据角平分线和对顶角相等得出∠CEF=∠CFE,即可得出EC=FC,再利用相似三角形的判定与性质得出答案.
【解答】解:过点F作FG⊥AB于点G,
∵∠ACB=90°,CD⊥AB,
∴∠CDB=90°,
∴∠CBF+∠CFB=90°,∠FBD+∠BED=90°,
∵BF平分∠CBA,
∴∠CBF=∠FBD,
∴∠CFB=∠BED=∠CEF,
∴CE=CF,
∵BF平分∠CBA,∠BCF=∠BGF=90°,
∴FC=FG,
∵∠A=∠A,∠FGA=∠ACB=90°,
∴△AFG∽△ABC,
∴=,
∵BC=6,AB=10,∠ACB=90°,
∴AC=8,
∴=,
∵FC=FG,
∴=,
解得:FC=3,
即CE的长为3.
补充方法:设CF=FG=x,在Rt△AFG中,∵AF2=FG2+AG2,
∴(8﹣x)2=x2+42,
解得x=3,
∴CE=CF=3.
故选:A.
二、准确填空(本大题共6个小题,每小题3分,共18分.请你把答案写在横线上)
13.(3分)8的立方根是 2 .
【分析】利用立方根的定义计算即可得到结果.
【解答】解:8的立方根为2,
故答案为:2.
14.(3分)如图所示的五角星是轴对称图形,它的对称轴共有 5 条.
【分析】根据如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.
【解答】解:五角星的对称轴共有5条,
故答案为:5.
15.(3分)计算:= 4 .
【分析】利用平方差公式计算.
【解答】解:原式=5﹣1
=4.
故答案为4.
16.(3分)如图,OC为∠AOB的平分线,CM⊥OB,OC=5,OM=4,则点C到射线OA的距离为 3 .
【分析】过C作CF⊥AO,根据勾股定理可得CM的长,再根据角的平分线上的点到角的两边的距离相等可得CF=CM,进而可得答案.
【解答】解:过C作CF⊥AO,
∵OC为∠AOB的平分线,CM⊥OB,
∴CM=CF,
∵OC=5,OM=4,
∴CM=3,
∴CF=3,
故答案为:3.
17.(3分)若关于x的分式方程有增根,则m的值为 1 .
【分析】增根是化为整式方程后产生的不适合分式方程的根.所以应先确定增根的可能值,让最简公分母x﹣3=0,得到x=3,然后代入化为整式方程的方程算出m的值.
【解答】解:方程两边都乘x﹣3,
得x﹣3m=2m(x﹣3)
∵原方程有增根,
∴最简公分母x﹣3=0,
解得x=3,
当x=3时,m=1
故m的值是1,
故答案为:1
18.(3分)如图,△ACB和△DCE都是等腰直角三角形,AC=BC,DC=EC,△ACB的顶点A在△DCE的斜边DE上,若AD=,AE=,则BC= 2 .
【分析】由等腰三角形的性质可得AC=BC,DC=EC,∠DCE=∠ACB=90°,∠D=∠CED=45°,可证△ADC≌△BEC,可得AD=BE=,∠D=∠BEC=45°,由勾股定理可求AB=2,即可求BC的长.
【解答】证明:如图,连接BE,
∵△ACB和△DCE都是等腰直角三角形
∴AC=BC,DC=EC,∠DCE=∠ACB=90°,∠D=∠CED=45°
∴∠DCA=∠BCE,且AC=BC,DC=EC,
∴△ADC≌△BEC(SAS)
∴AD=BE=,∠D=∠BEC=45°,
∴∠AEB=90°
∴AB==2
∵AB=BC
∴BC=2
故答案为:2
三、挑战技能(本大题共4个小题,每小题6分,共24分)
19.(6分)计算:
【分析】先进行二次根式的乘法运算,然后取绝对值后合并即可.
【解答】解:原式=﹣+﹣1
=﹣3+﹣1
=﹣﹣1.
20.(6分)已知:如图,∠A=∠D=90°,AC=DB,AC、DB相交于点O.
求证:△OBC是等腰三角形.
【分析】由“HL”可证Rt△ABC≌Rt△DBC,可得∠ACB=∠DBC,可证△OBC是等腰三角形.
【解答】证明:∵AC=DB,BC=BC
∴Rt△ABC≌Rt△DBC(HL)
∴∠ACB=∠DBC
∴OB=OC
∴△OBC是等腰三角形
21.(6分)顶点都在格点上的三角形叫做格点三角形,如图,在4×4的方格纸中,△ABC是格点三角形.
(1)在图1中,以点C为对称中心,作出一个与△ABC成中心对称的格点三角形DEC,在题后横线上直接写出AB与DE的位置关系: AB∥DE,AB=DE ;
(2)在图2中,以AC所在的直线为对称轴,作出一个与△ABC成轴对称的格点三角形AFC,并在后横线上直接写出△BCF是什么形状的特殊三角形: 等腰直角三角形 .
【分析】(1)根据中心对称的性质画出图形即可判断.
(2)根据轴对称的性质画出图形即可判断.
【解答】解:(1)△DEC即为所求.AB∥DE,AB=DE.
故答案为AB∥DE,AB=DE.
(2)△ACF即为所求.
△BCF是等腰直角三角形.
故答案为:等腰直角三角形.
22.(6分)当x﹣y=2时,求的值.
【分析】首先对分式进行化简,然后将x﹣y=2时代入即可.
【解答】解:
=
=
=
=,
x﹣y=2时.
.
第二部分实践与应用
23.(8分)《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,来折抵地,去本三尺,问折者高几何?“译成数学问题是:如图所示,在△ABC中,∠ACB=90°,AC+AB=1丈,BC=3尺,求AC的长为多少尺?(说明:1丈=10尺)
【分析】设AC=x,可知AB=10﹣x,再根据勾股定理即可得出结论.
【解答】解:1丈=10尺,
设AC=x,
∵AC+AB=10,
∴AB=10﹣x.
∵在Rt△ABC中,∠ACB=90°,
∴AC2+BC2=AB2,即x2+32=(10﹣x)2.
解得:x=4.55,
即AC=4.55尺.
24.(8分)观察下列各式:
请利用你所发现的规律,解决下列问题:
(1)第4个算式为: ;
(2)求的值;
(3)诸直接写出的结果.
【分析】根据题目的规律进行计算即可.不难发现由根号形式转化为积的形式.因此
(1)可以猜想到接下来的第4个算式为:,
(2)题中可以根据题目进行每一项的转化.从而计算出结果;
(3)第(2)题进一步扩展到n项即可.详见解答过程.
【解答】解:
(1)依题意:接下来的第4个算式为:
故答案为
(2)原式=
=
=
=
(3)
原式=
=
=
=
25.(9分)已知:如图1,OM是∠AOB的平分线,点C在OM上,OC=5,且点C到OA的距离为3.过点C作CD⊥OA,CE⊥OB,垂足分别为D、E,易得到结论:OD+OE= 8 ;
(1)把图1中的∠DCE绕点C旋转,当CD与OA不垂直时(如图2),上述结论是否成立?并说明理由;
(2)把图1中的∠DCE绕点C旋转,当CD与OA的反向延长线相交于点D时:
①请在图3中画出图形;
②上述结论还成立吗?若成立,请给出证明;若不成立,请直接写出线段OD、OE之间的数量关系,不需证明.
【分析】先利用勾股定理求出OD,再利用角平分线定理得出DE=CD,即可得出结论;
(1)先判断出∠DCQ=∠ECP,进而判断出△CQD≌△CPE,得出DQ=PE,即可得出结论;
(2)①依题意即可补全图形;
②同(1)的方法即可得出结论.
【解答】解:∵CD⊥OA,
∴∠ODC=90°,
在Rt△ODC中,CD=3,OC=5,
∴OD==4,
∵点C是∠AOB的平分线上的点,
∴DE=CD=3,
同理,OE=4,
∴OD+OE=4+4=8,
故答案为8;
(1)上述结论成立,理由:如图2,过点C作CQ⊥OA于Q,CP⊥OB于P,
∴∠OQC=∠EPC=90°,
∴∠AOB+∠POQ=180°,
由旋转知,∠AOB+∠DOE=180°,
∴∠POQ=∠DOE,
∴∠DCQ=∠ECP,
∵点C是∠AOB的平分线上,且CQ⊥OA,CP⊥OB,
∴CQ=CP,
∵∠OQC=∠EPC=90°,
∴△CQD≌△CPE(ASA),
∴DQ=PE,
∵OD=OQ﹣DQ,OE=OP+PE,
∴OD+OE=OQ﹣DQ+OP+PE=OQ+OP=8;
(2)①补全图形如图3,
②上述结论不成立,OE﹣OD=8,
理由:过点C作CQ⊥OA于Q,CP⊥OB于P,
∴∠OQC=∠EPC=90°,
∴∠AOB+∠POQ=180°,
由旋转知,∠AOB+∠DOE=180°,
∴∠POQ=∠DOE,
∴∠DCQ=∠ECP,
∵点C是∠AOB的平分线上,且CQ⊥OA,CP⊥OB,
∴CQ=CP,
∵∠OQC=∠EPC=90°,
∴△CQD≌△CPE(ASA),
∴DQ=PE,
∵OD=DQ﹣OQ,OE=OP+PE,
∴OE﹣OD=OP+PE﹣(DQ﹣OQ)=OP+PE﹣DQ+OQ=OP+OQ=8.
26.(9分)如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,E为AB边的中点,以BE为边作等边△BDE,连接AD、CD.
(1)求证:AD=CD;
(2)①画图:在AC边上找一点H,使得BH+EH最小(要求:写出作图过程并画出图形,不用说明作图依据);
②当BC=2时,求出BH+EH的最小值.
【分析】(1)证明△ABC≌△ABD(SAS),可得AC=AD.
(2)①作点B关于直线AC的对称点B′,连接EB′交AC于H,点H即为所求.
②连接AB′,证明△ABB′是等边三角形即可解决问题.
【解答】(1)证明:∵∠ACB=90°,∠BAC=30°,
∴AB=2BC,∠ABC=60°
∵AE=EB,
∴BC=BE,
∵△BED是等边三角形,
∴BE=BD,∠ABD=60°,
∵AB=AB,∠ABC=∠ABD=60°,BC=BD,
∴△ABC≌△ABD(SAS),
∴AC=AD.
(2)①作点B关于直线AC的对称点B′,连接EB′交AC于H,点H即为所求.
②连接AB′,
∵AC⊥BB′,CB=CB′,
∴AB=AB′,
∵∠ABC=60°,
∴△ABB′是等边三角形,
∵AE=EB,
∴B′E⊥AB,
在Rt△BEB′中,∵BB′=4,∠EBB′=60°,
∴EB′=BB′?sin60°=2,
∴EH+HB的最小值=EH+HB′=EB′=2
一、精心选择(本大题共12个小题,每小题2分,共24分.在每小题给出的四个选项中,只有一项是正确的,请在答题卡上把正确选项的标号用2B铅缩涂黑)
1.(2分)式子有意义,则x的取值范围是( )
A.x>1
B.x<1
C.x≥1
D.x≤1
2.(2分)在下列图形中,中心对称图形是( )
A.
B.
C.
D.
3.(2分)若分式的值为0,则x的值是( )
A.3或﹣3
B.﹣3
C.0
D.3
4.(2分)小亮用天平称得一个鸡蛋的质量为50.47g,用四舍五入法将50.47精确到0.1的近似值为( )
A.50
B.50.0
C.50.4
D.50.5
5.(2分)已知a、b、c为三角形的边长,则图2中甲、乙、丙三个三角形和图1中的△ABC全等的是( )
A.甲和乙
B.乙和丙
C.甲和丙
D.只有丙
6.(2分)估计的值在( )
A.2和3之间
B.3和4之间
C.4和5之间
D.5和6之间
7.(2分)如图,在△ABC中,AB=AC,AD、CE分别是△ABC的中线和角平分线,当∠ACE=35°时,∠BAD的度数是( )
A.55°
B.40°
C.35°
D.20°
8.(2分)下列等式正确的是( )
A.
B.
C.
D.
9.(2分)在用反证法证明“三角形的最大内角不小于60°”时,假设三角形的最大内角不小于60°不成立,则有三角形的最大内角( )
A.小于60°
B.等于60°
C.大于60°
D.大于或等于60°
10.(2分)=( )
A.
B.
C.
D.
11.(2分)如图,在△ABC中,DE是AC的垂直平分线,且分别交BC、AC于D、E两点,∠B=60°,∠BAD=70°,则∠BAC的度数为( )
A.130°
B.95°
C.90°
D.85°
12.(2分)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,BF平分∠ABC,交CD于点E,交AC于点F.若AB=10,BC=6,则CE的长为( )
A.3
B.4
C.5
D.6
二、准确填空(本大题共6个小题,每小题3分,共18分.请你把答案写在横线上)
13.(3分)8的立方根是
.
14.(3分)如图所示的五角星是轴对称图形,它的对称轴共有
条.
15.(3分)计算:=
.
16.(3分)如图,OC为∠AOB的平分线,CM⊥OB,OC=5,OM=4,则点C到射线OA的距离为
.
17.(3分)若关于x的分式方程有增根,则m的值为
.
18.(3分)如图,△ACB和△DCE都是等腰直角三角形,AC=BC,DC=EC,△ACB的顶点A在△DCE的斜边DE上,若AD=,AE=,则BC=
.
三、挑战技能(本大题共4个小题,每小题6分,共24分)
19.(6分)计算:
20.(6分)已知:如图,∠A=∠D=90°,AC=DB,AC、DB相交于点O.
求证:△OBC是等腰三角形.
21.(6分)顶点都在格点上的三角形叫做格点三角形,如图,在4×4的方格纸中,△ABC是格点三角形.
(1)在图1中,以点C为对称中心,作出一个与△ABC成中心对称的格点三角形DEC,在题后横线上直接写出AB与DE的位置关系:
;
(2)在图2中,以AC所在的直线为对称轴,作出一个与△ABC成轴对称的格点三角形AFC,并在后横线上直接写出△BCF是什么形状的特殊三角形:
.
22.(6分)当x﹣y=2时,求的值.
第二部分实践与应用
23.(8分)《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,来折抵地,去本三尺,问折者高几何?“译成数学问题是:如图所示,在△ABC中,∠ACB=90°,AC+AB=1丈,BC=3尺,求AC的长为多少尺?(说明:1丈=10尺)
24.(8分)观察下列各式:
请利用你所发现的规律,解决下列问题:
(1)第4个算式为:
;
(2)求的值;
(3)诸直接写出的结果.
25.(9分)已知:如图1,OM是∠AOB的平分线,点C在OM上,OC=5,且点C到OA的距离为3.过点C作CD⊥OA,CE⊥OB,垂足分别为D、E,易得到结论:OD+OE=
;
(1)把图1中的∠DCE绕点C旋转,当CD与OA不垂直时(如图2),上述结论是否成立?并说明理由;
(2)把图1中的∠DCE绕点C旋转,当CD与OA的反向延长线相交于点D时:
①请在图3中画出图形;
②上述结论还成立吗?若成立,请给出证明;若不成立,请直接写出线段OD、OE之间的数量关系,不需证明.
26.(9分)如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,E为AB边的中点,以BE为边作等边△BDE,连接AD、CD.
(1)求证:AD=CD;
(2)①画图:在AC边上找一点H,使得BH+EH最小(要求:写出作图过程并画出图形,不用说明作图依据);
②当BC=2时,求出BH+EH的最小值.
参考答案与试题解析
一、精心选择(本大题共12个小题,每小题2分,共24分.在每小题给出的四个选项中,只有一项是正确的,请在答题卡上把正确选项的标号用2B铅缩涂黑)
1.(2分)式子有意义,则x的取值范围是( )
A.x>1
B.x<1
C.x≥1
D.x≤1
【分析】根据二次根式的被开方数是非负数列出不等式x﹣1≥0,通过解该不等式即可求得x的取值范围.
【解答】解:根据题意,得x﹣1≥0,
解得,x≥1.
故选:C.
2.(2分)在下列图形中,中心对称图形是( )
A.
B.
C.
D.
【分析】根据中心对称图形的概念求解.
【解答】解:A.不是中心对称图形,故此选项错误;
B.不是中心对称图形,故此选项错误;
C.不是中心对称图形,故此选项错误;
D.是中心对称图形,故此选项正确;
故选:D.
3.(2分)若分式的值为0,则x的值是( )
A.3或﹣3
B.﹣3
C.0
D.3
【分析】根据分式的值为零的条件可以求出x的值.
【解答】解:依题意得:x2﹣9=0且x≠0,
解得x=±3.
故选:A.
4.(2分)小亮用天平称得一个鸡蛋的质量为50.47g,用四舍五入法将50.47精确到0.1的近似值为( )
A.50
B.50.0
C.50.4
D.50.5
【分析】根据四舍五入法可以解答本题.
【解答】解:50.47≈50.5(精确到0.1),
故选:D.
5.(2分)已知a、b、c为三角形的边长,则图2中甲、乙、丙三个三角形和图1中的△ABC全等的是( )
A.甲和乙
B.乙和丙
C.甲和丙
D.只有丙
【分析】首先观察图形,然后根据三角形全等的判定方法(AAS与SAS),即可求得答案.
【解答】解:如图:
在△ABC和△MNK中,,
∴△ABC≌△NKM(SAS);
在△ABC和△HIG中,,
∴△ABC≌△GHI(AAS).
∴甲、乙、丙三个三角形中和△ABC全等的图形是:乙和丙.
故选:B.
6.(2分)估计的值在( )
A.2和3之间
B.3和4之间
C.4和5之间
D.5和6之间
【分析】直接得出的取值范围进而得出答案.
【解答】解:∵,
∴,
故选:C.
7.(2分)如图,在△ABC中,AB=AC,AD、CE分别是△ABC的中线和角平分线,当∠ACE=35°时,∠BAD的度数是( )
A.55°
B.40°
C.35°
D.20°
【分析】根据角平分线的定义和等腰三角形的性质即可得到结论.
【解答】解:∵CE是∠ACB的平分线,∠ACE=35°,
∴∠ACB=2∠ACE=70°,
∵AB=AC,
∴∠B=∠ACB=70°,
∵AD⊥BC,
∴∠ADB=90°,
∴∠BAD=90°﹣∠B=20°,
故选:D.
8.(2分)下列等式正确的是( )
A.
B.
C.
D.
【分析】根据二次根式的性质1和性质2逐一判断即可得.
【解答】解:A.=2,故本选项不符合题意;
B.()2=2,故本选项符合题意;
C.﹣=﹣2,故本选项不符合题意;
D.(﹣)2=2,故本选项不符合题意;
故选:B.
9.(2分)在用反证法证明“三角形的最大内角不小于60°”时,假设三角形的最大内角不小于60°不成立,则有三角形的最大内角( )
A.小于60°
B.等于60°
C.大于60°
D.大于或等于60°
【分析】根据反证法的步骤,从命题的反面出发假设出结论.
【解答】解:在用反证法证明“三角形的最大内角不小于60°”时,
假设三角形的最大内角不小于60°不成立,则有三角形的最大内角小于60°.
故选:A.
10.(2分)=( )
A.
B.
C.
D.
【分析】根据二次根式的性质4化简可得.
【解答】解:===,
故选:D.
11.(2分)如图,在△ABC中,DE是AC的垂直平分线,且分别交BC、AC于D、E两点,∠B=60°,∠BAD=70°,则∠BAC的度数为( )
A.130°
B.95°
C.90°
D.85°
【分析】根据线段垂直平分线的性质得到DA=DC,根据等腰三角形的性质得到∠DAC=∠C,根据三角形内角和定理求出∠BDA的度数,计算出结果.
【解答】解:∵DE是AC的垂直平分线,
∴DA=DC,
∴∠DAC=∠C,
∵∠B=60°,∠BAD=70°,
∴∠BDA=50°,
∴∠DAC=∠BDA=25°,
∴∠BAC=∠BAD+∠DAC=70°+25°=95°
故选:B.
12.(2分)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,BF平分∠ABC,交CD于点E,交AC于点F.若AB=10,BC=6,则CE的长为( )
A.3
B.4
C.5
D.6
【分析】根据三角形的内角和定理得出∠CBF+∠CFB=90°,∠FBD+∠BED=90°,根据角平分线和对顶角相等得出∠CEF=∠CFE,即可得出EC=FC,再利用相似三角形的判定与性质得出答案.
【解答】解:过点F作FG⊥AB于点G,
∵∠ACB=90°,CD⊥AB,
∴∠CDB=90°,
∴∠CBF+∠CFB=90°,∠FBD+∠BED=90°,
∵BF平分∠CBA,
∴∠CBF=∠FBD,
∴∠CFB=∠BED=∠CEF,
∴CE=CF,
∵BF平分∠CBA,∠BCF=∠BGF=90°,
∴FC=FG,
∵∠A=∠A,∠FGA=∠ACB=90°,
∴△AFG∽△ABC,
∴=,
∵BC=6,AB=10,∠ACB=90°,
∴AC=8,
∴=,
∵FC=FG,
∴=,
解得:FC=3,
即CE的长为3.
补充方法:设CF=FG=x,在Rt△AFG中,∵AF2=FG2+AG2,
∴(8﹣x)2=x2+42,
解得x=3,
∴CE=CF=3.
故选:A.
二、准确填空(本大题共6个小题,每小题3分,共18分.请你把答案写在横线上)
13.(3分)8的立方根是 2 .
【分析】利用立方根的定义计算即可得到结果.
【解答】解:8的立方根为2,
故答案为:2.
14.(3分)如图所示的五角星是轴对称图形,它的对称轴共有 5 条.
【分析】根据如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.
【解答】解:五角星的对称轴共有5条,
故答案为:5.
15.(3分)计算:= 4 .
【分析】利用平方差公式计算.
【解答】解:原式=5﹣1
=4.
故答案为4.
16.(3分)如图,OC为∠AOB的平分线,CM⊥OB,OC=5,OM=4,则点C到射线OA的距离为 3 .
【分析】过C作CF⊥AO,根据勾股定理可得CM的长,再根据角的平分线上的点到角的两边的距离相等可得CF=CM,进而可得答案.
【解答】解:过C作CF⊥AO,
∵OC为∠AOB的平分线,CM⊥OB,
∴CM=CF,
∵OC=5,OM=4,
∴CM=3,
∴CF=3,
故答案为:3.
17.(3分)若关于x的分式方程有增根,则m的值为 1 .
【分析】增根是化为整式方程后产生的不适合分式方程的根.所以应先确定增根的可能值,让最简公分母x﹣3=0,得到x=3,然后代入化为整式方程的方程算出m的值.
【解答】解:方程两边都乘x﹣3,
得x﹣3m=2m(x﹣3)
∵原方程有增根,
∴最简公分母x﹣3=0,
解得x=3,
当x=3时,m=1
故m的值是1,
故答案为:1
18.(3分)如图,△ACB和△DCE都是等腰直角三角形,AC=BC,DC=EC,△ACB的顶点A在△DCE的斜边DE上,若AD=,AE=,则BC= 2 .
【分析】由等腰三角形的性质可得AC=BC,DC=EC,∠DCE=∠ACB=90°,∠D=∠CED=45°,可证△ADC≌△BEC,可得AD=BE=,∠D=∠BEC=45°,由勾股定理可求AB=2,即可求BC的长.
【解答】证明:如图,连接BE,
∵△ACB和△DCE都是等腰直角三角形
∴AC=BC,DC=EC,∠DCE=∠ACB=90°,∠D=∠CED=45°
∴∠DCA=∠BCE,且AC=BC,DC=EC,
∴△ADC≌△BEC(SAS)
∴AD=BE=,∠D=∠BEC=45°,
∴∠AEB=90°
∴AB==2
∵AB=BC
∴BC=2
故答案为:2
三、挑战技能(本大题共4个小题,每小题6分,共24分)
19.(6分)计算:
【分析】先进行二次根式的乘法运算,然后取绝对值后合并即可.
【解答】解:原式=﹣+﹣1
=﹣3+﹣1
=﹣﹣1.
20.(6分)已知:如图,∠A=∠D=90°,AC=DB,AC、DB相交于点O.
求证:△OBC是等腰三角形.
【分析】由“HL”可证Rt△ABC≌Rt△DBC,可得∠ACB=∠DBC,可证△OBC是等腰三角形.
【解答】证明:∵AC=DB,BC=BC
∴Rt△ABC≌Rt△DBC(HL)
∴∠ACB=∠DBC
∴OB=OC
∴△OBC是等腰三角形
21.(6分)顶点都在格点上的三角形叫做格点三角形,如图,在4×4的方格纸中,△ABC是格点三角形.
(1)在图1中,以点C为对称中心,作出一个与△ABC成中心对称的格点三角形DEC,在题后横线上直接写出AB与DE的位置关系: AB∥DE,AB=DE ;
(2)在图2中,以AC所在的直线为对称轴,作出一个与△ABC成轴对称的格点三角形AFC,并在后横线上直接写出△BCF是什么形状的特殊三角形: 等腰直角三角形 .
【分析】(1)根据中心对称的性质画出图形即可判断.
(2)根据轴对称的性质画出图形即可判断.
【解答】解:(1)△DEC即为所求.AB∥DE,AB=DE.
故答案为AB∥DE,AB=DE.
(2)△ACF即为所求.
△BCF是等腰直角三角形.
故答案为:等腰直角三角形.
22.(6分)当x﹣y=2时,求的值.
【分析】首先对分式进行化简,然后将x﹣y=2时代入即可.
【解答】解:
=
=
=
=,
x﹣y=2时.
.
第二部分实践与应用
23.(8分)《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,来折抵地,去本三尺,问折者高几何?“译成数学问题是:如图所示,在△ABC中,∠ACB=90°,AC+AB=1丈,BC=3尺,求AC的长为多少尺?(说明:1丈=10尺)
【分析】设AC=x,可知AB=10﹣x,再根据勾股定理即可得出结论.
【解答】解:1丈=10尺,
设AC=x,
∵AC+AB=10,
∴AB=10﹣x.
∵在Rt△ABC中,∠ACB=90°,
∴AC2+BC2=AB2,即x2+32=(10﹣x)2.
解得:x=4.55,
即AC=4.55尺.
24.(8分)观察下列各式:
请利用你所发现的规律,解决下列问题:
(1)第4个算式为: ;
(2)求的值;
(3)诸直接写出的结果.
【分析】根据题目的规律进行计算即可.不难发现由根号形式转化为积的形式.因此
(1)可以猜想到接下来的第4个算式为:,
(2)题中可以根据题目进行每一项的转化.从而计算出结果;
(3)第(2)题进一步扩展到n项即可.详见解答过程.
【解答】解:
(1)依题意:接下来的第4个算式为:
故答案为
(2)原式=
=
=
=
(3)
原式=
=
=
=
25.(9分)已知:如图1,OM是∠AOB的平分线,点C在OM上,OC=5,且点C到OA的距离为3.过点C作CD⊥OA,CE⊥OB,垂足分别为D、E,易得到结论:OD+OE= 8 ;
(1)把图1中的∠DCE绕点C旋转,当CD与OA不垂直时(如图2),上述结论是否成立?并说明理由;
(2)把图1中的∠DCE绕点C旋转,当CD与OA的反向延长线相交于点D时:
①请在图3中画出图形;
②上述结论还成立吗?若成立,请给出证明;若不成立,请直接写出线段OD、OE之间的数量关系,不需证明.
【分析】先利用勾股定理求出OD,再利用角平分线定理得出DE=CD,即可得出结论;
(1)先判断出∠DCQ=∠ECP,进而判断出△CQD≌△CPE,得出DQ=PE,即可得出结论;
(2)①依题意即可补全图形;
②同(1)的方法即可得出结论.
【解答】解:∵CD⊥OA,
∴∠ODC=90°,
在Rt△ODC中,CD=3,OC=5,
∴OD==4,
∵点C是∠AOB的平分线上的点,
∴DE=CD=3,
同理,OE=4,
∴OD+OE=4+4=8,
故答案为8;
(1)上述结论成立,理由:如图2,过点C作CQ⊥OA于Q,CP⊥OB于P,
∴∠OQC=∠EPC=90°,
∴∠AOB+∠POQ=180°,
由旋转知,∠AOB+∠DOE=180°,
∴∠POQ=∠DOE,
∴∠DCQ=∠ECP,
∵点C是∠AOB的平分线上,且CQ⊥OA,CP⊥OB,
∴CQ=CP,
∵∠OQC=∠EPC=90°,
∴△CQD≌△CPE(ASA),
∴DQ=PE,
∵OD=OQ﹣DQ,OE=OP+PE,
∴OD+OE=OQ﹣DQ+OP+PE=OQ+OP=8;
(2)①补全图形如图3,
②上述结论不成立,OE﹣OD=8,
理由:过点C作CQ⊥OA于Q,CP⊥OB于P,
∴∠OQC=∠EPC=90°,
∴∠AOB+∠POQ=180°,
由旋转知,∠AOB+∠DOE=180°,
∴∠POQ=∠DOE,
∴∠DCQ=∠ECP,
∵点C是∠AOB的平分线上,且CQ⊥OA,CP⊥OB,
∴CQ=CP,
∵∠OQC=∠EPC=90°,
∴△CQD≌△CPE(ASA),
∴DQ=PE,
∵OD=DQ﹣OQ,OE=OP+PE,
∴OE﹣OD=OP+PE﹣(DQ﹣OQ)=OP+PE﹣DQ+OQ=OP+OQ=8.
26.(9分)如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,E为AB边的中点,以BE为边作等边△BDE,连接AD、CD.
(1)求证:AD=CD;
(2)①画图:在AC边上找一点H,使得BH+EH最小(要求:写出作图过程并画出图形,不用说明作图依据);
②当BC=2时,求出BH+EH的最小值.
【分析】(1)证明△ABC≌△ABD(SAS),可得AC=AD.
(2)①作点B关于直线AC的对称点B′,连接EB′交AC于H,点H即为所求.
②连接AB′,证明△ABB′是等边三角形即可解决问题.
【解答】(1)证明:∵∠ACB=90°,∠BAC=30°,
∴AB=2BC,∠ABC=60°
∵AE=EB,
∴BC=BE,
∵△BED是等边三角形,
∴BE=BD,∠ABD=60°,
∵AB=AB,∠ABC=∠ABD=60°,BC=BD,
∴△ABC≌△ABD(SAS),
∴AC=AD.
(2)①作点B关于直线AC的对称点B′,连接EB′交AC于H,点H即为所求.
②连接AB′,
∵AC⊥BB′,CB=CB′,
∴AB=AB′,
∵∠ABC=60°,
∴△ABB′是等边三角形,
∵AE=EB,
∴B′E⊥AB,
在Rt△BEB′中,∵BB′=4,∠EBB′=60°,
∴EB′=BB′?sin60°=2,
∴EH+HB的最小值=EH+HB′=EB′=2
同课章节目录
