初中数学北师大版七年级下册第四章三角形复习课2课件(共30张PPT)
文档属性
| 名称 | 初中数学北师大版七年级下册第四章三角形复习课2课件(共30张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 00:00:00 | ||
图片预览





文档简介
初中数学七年级(下)
第四章 三角形复习课二
1.已知三角形的三边长分别为a、b、c,化简|a +b﹣c|﹣2|a﹣b﹣c|+|a+b+c|得( )
A.2a﹣2b﹣c B.4a﹣2c C.4b+2c D.2a﹣2b+c
2 .如图1,在△ABC中,AD平分∠BAC,EG⊥AD,且分别交AB、AD、
AC及BC的延长线于点E、H、F、G,若∠B=45°,∠ACB=75°,
则∠G的度数为( )
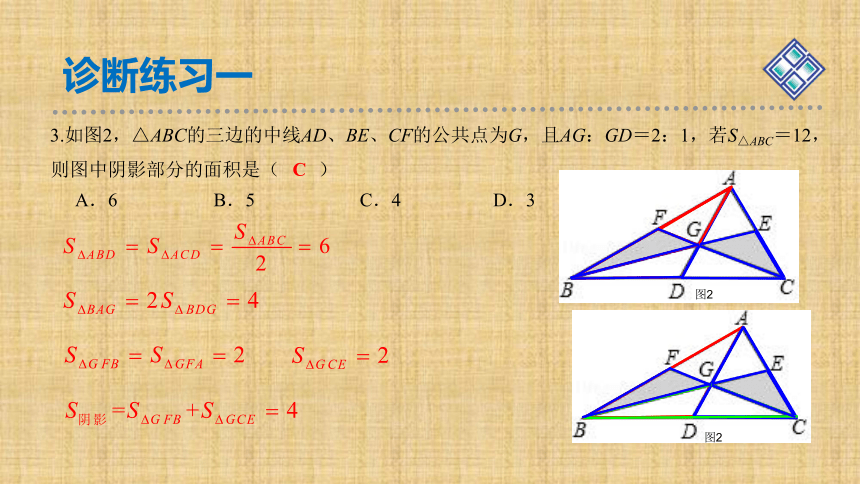
3.如图2,△ABC的三边的中线AD、BE、CF的公共点为G,且
AG:GD=2:1,若S△ABC=12,则图中阴影部分的面积是( )
A.6 B.5 C.4 D.3
A.15° B.22.5° C.27.5° D.30°
图1
图2
诊断练习一
4.如图3,已知线段AB、CD相交于点O,连接AD、CB,我们把形
如图3的图形称之为“8字形”.如图4,在图3的条件下,∠DAB
和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交
于点M、N,试解答下列问题:
(1)在图3中,求出∠A、∠B、∠C、∠D之间的数量关系;
(2)在图4中,若∠B=40°,∠D=36°,试求∠P的度数;
(3)如果图4中∠D和∠B为任意角时,其他条件不变,试问∠P
与∠D、∠B之间存在着怎样的数量关系.
图3
图4
能力提高一
解:∵△ABC的三边长a、b、c需满足两边之和大于第三边,两边之差小于第三边,
∴a+b﹣c>0,a﹣b﹣c<0,a+b+c>0.
∴|a+b﹣c|=a+b﹣c,|a﹣b﹣c|=b+c﹣a,|a+b+c|=a+b+c.
∴|a+b﹣c|﹣2|a﹣b﹣c|+|a+b+c|=(a+b﹣c)﹣2(b+c﹣a)+(a+b+c)=4a﹣2c.
1.已知三角形的三边长分别为a、b、c,化简|a +b﹣c|﹣2|a﹣b﹣c|+|a+b+c|得( )
A.2a﹣2b﹣c B.4a﹣2c C.4b+2c D.2a﹣2b+c
B
诊断练习一
图1
∴∠HAF+∠AFE=90°.
∴∠AFE=90°-∠HAF=60°.
∵∠AFE与∠GFC是对顶角,
∴∠GFC=∠AFE=60°.
∵∠ACB=75°,
∴∠ACG=180°-∠ACB=180°-75°=105°.
∵∠G+∠GFC+∠GCF=180°,
∴∠G=180°-∠GFC-∠GCF=180°-60°-105°=15°.
2 .如图1,在△ABC中,AD平分∠BAC,EG⊥AD,且分别交
AB、AD、AC及BC的延长线于点E、H、F、G,若∠B=45°,
∠ACB=75°,则∠G的度数为( )
A.15° B.22.5° C.27.5° D.30°
解:∵∠BAC+∠B+∠ACB=180°,
∴∠BAC=180°-∠B-∠ACB.
∵∠B=45°,∠ACB=75°,
∴∠BAC=60°.
∵AD平分∠BAC,
∴∠CAD= =30°.
∵EG⊥AD,
A
诊断练习一
3.如图2,△ABC的三边的中线AD、BE、CF的公共点为G,且AG:GD=2:1,若S△ABC=12,则图中阴影部分的面积是( )
A.6 B.5 C.4 D.3
图2
C
诊断练习一
图2
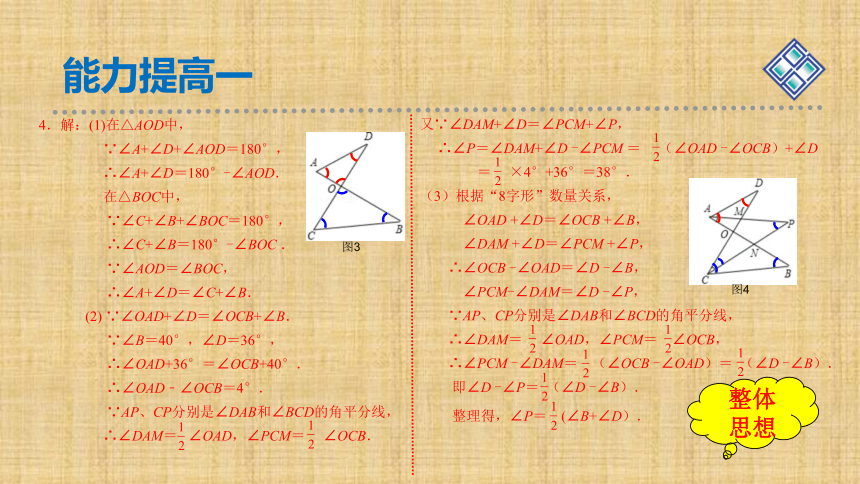
4.解:(1)在△AOD中,
∵∠A+∠D+∠AOD=180°,
∴∠A+∠D=180°-∠AOD.
在△BOC中,
∵∠C+∠B+∠BOC=180°,
∴∠C+∠B=180°-∠BOC .
∵∠AOD=∠BOC,
∴∠A+∠D=∠C+∠B.
(2) ∵∠OAD+∠D=∠OCB+∠B.
∵∠B=40°,∠D=36°,
∴∠OAD+36°=∠OCB+40°.
∴∠OAD﹣∠OCB=4°.
∵AP、CP分别是∠DAB和∠BCD的角平分线,
∴∠DAM= ∠OAD,∠PCM= ∠OCB.
,
又∵∠DAM+∠D=∠PCM+∠P,
∴∠P=∠DAM+∠D -∠PCM = (∠OAD -∠OCB)+∠D
= ×4°+36°=38°.
(3)根据“8字形”数量关系,
∠OAD +∠D=∠OCB +∠B,
∠DAM +∠D=∠PCM +∠P,
∴∠OCB -∠OAD=∠D -∠B,
∠PCM-∠DAM=∠D -∠P,
∵AP、CP分别是∠DAB和∠BCD的角平分线,
∴∠DAM= ∠OAD,∠PCM= ∠OCB,
∴∠PCM -∠DAM= (∠OCB -∠OAD)= (∠D -∠B).
即∠D -∠P= (∠D -∠B).
整理得,∠P= (∠B+∠D).
图3
图4
能力提高一
整体
思想
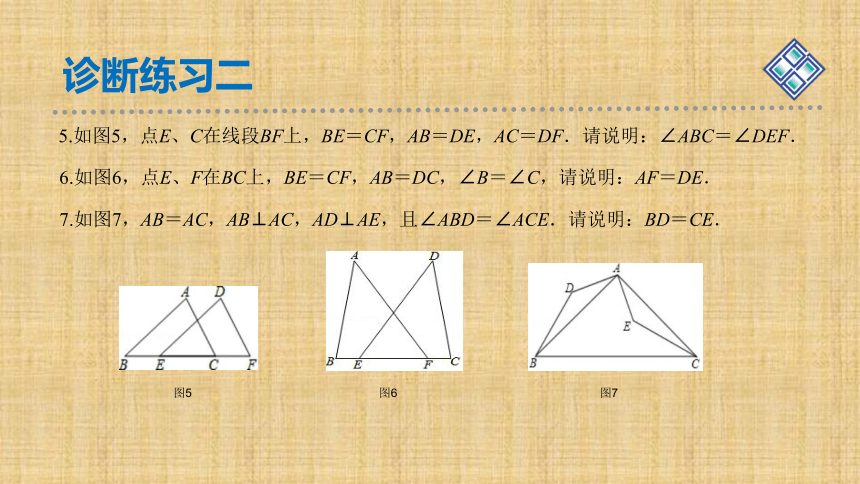
5.如图5,点E、C在线段BF上,BE=CF,AB=DE,AC=DF.请说明:∠ABC=∠DEF.
6.如图6,点E、F在BC上,BE=CF,AB=DC,∠B=∠C,请说明:AF=DE.
7.如图7,AB=AC,AB⊥AC,AD⊥AE,且∠ABD=∠ACE.请说明:BD=CE.
图5
图6
图7
诊断练习二
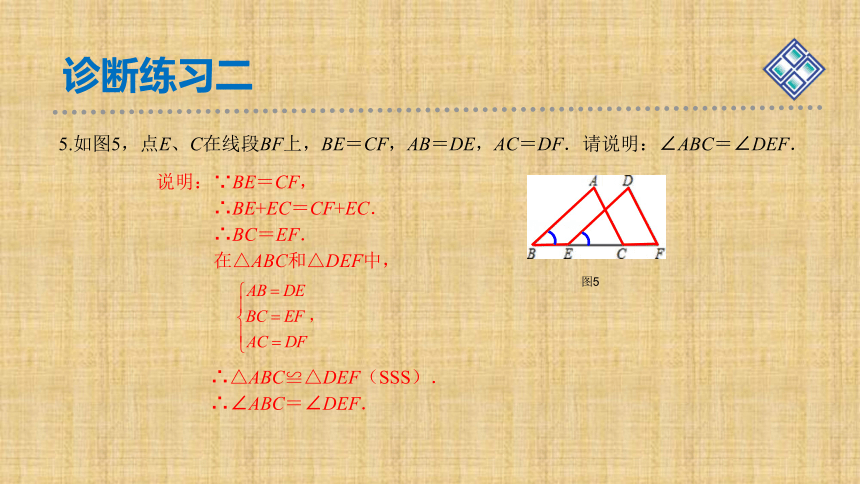
5.如图5,点E、C在线段BF上,BE=CF,AB=DE,AC=DF.请说明:∠ABC=∠DEF.
说明:∵BE=CF,
∴BE+EC=CF+EC.
∴BC=EF.
在△ABC和△DEF中,
∴△ABC≌△DEF(SSS).
∴∠ABC=∠DEF.
图5
诊断练习二
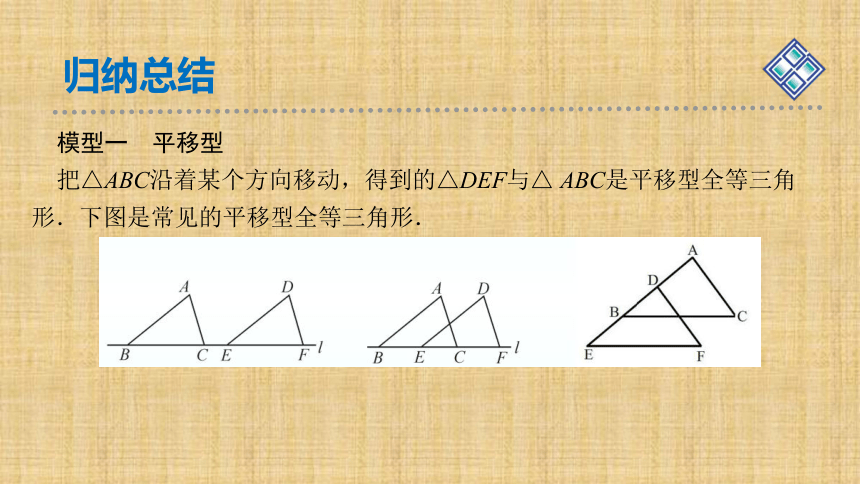
模型一 平移型
把△ABC沿着某个方向移动,得到的△DEF与△ ABC是平移型全等三角形.下图是常见的平移型全等三角形.
归纳总结
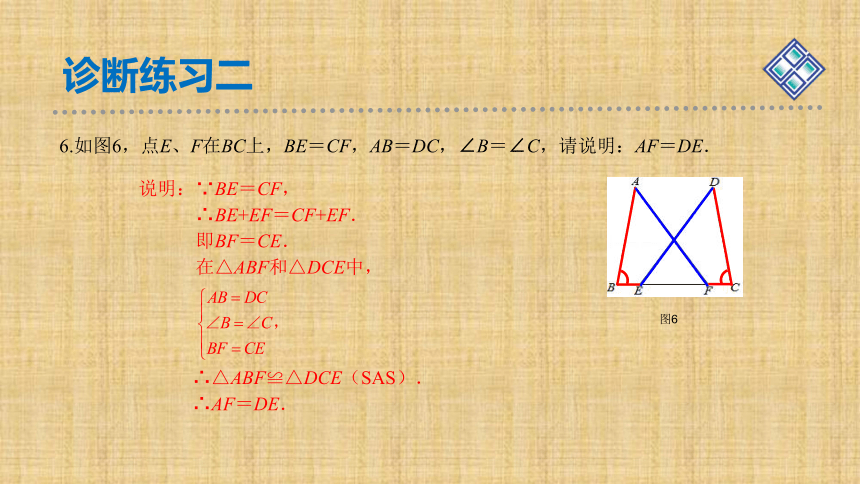
6.如图6,点E、F在BC上,BE=CF,AB=DC,∠B=∠C,请说明:AF=DE.
图6
说明:∵BE=CF,
∴BE+EF=CF+EF.
即BF=CE.
在△ABF和△DCE中,
∴△ABF≌△DCE(SAS).
∴AF=DE.
诊断练习二
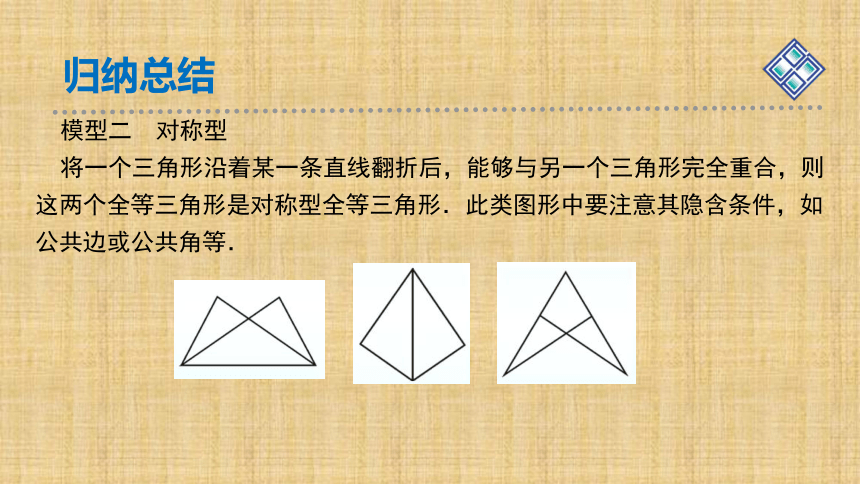
模型二 对称型
将一个三角形沿着某一条直线翻折后,能够与另一个三角形完全重合,则这两个全等三角形是对称型全等三角形.此类图形中要注意其隐含条件,如公共边或公共角等.
归纳总结
说明∵AB⊥AC,AD⊥AE,
∴∠BAC=∠DAE=90°.
∴∠BAC-∠BAE=∠DAE-∠BAE.
即∠BAD=∠CAE.
在△ABD和△ACE中,
7.如图7,AB=AC,AB⊥AC,AD⊥AE,且∠ABD=∠ACE.请说明:BD=CE.
∴△ABD≌△ACE(ASA).
∴BD=CE.
图7
诊断练习二
模型三 旋转型
旋转一定角度后,两个三角形能够完全重合,则这两个三角形可称为旋转型全等三角形.识别旋转型全等三角形时,如左图,涉及对顶角相等;中间图,涉及等角加(减)公共角;右图,涉及公共边问题.
归纳总结
8.如图8,Rt△ABC中,∠BAC=90°,AB=AC,分别过点B、C作过点A的直线的垂线BD、CE,垂足分别为D、E,若BD=3,CE=2,求DE的长.
诊断练习二
图8
解:∵∠BAC=90°,
∴∠BAD+∠CAE=90°.
∵BD⊥DE,
∴∠D=90°.
∴∠BAD+∠ABD=90°.
∴∠ABD=∠CAE.
∴△BDA≌△AEC(AAS).
∴DA=EC=2,BD=AE=3.
∴DE=DA+AE=5.
∵CE⊥DE,
∴∠E=90°.
∴∠D=∠E.
在△BDA和△AEC中,
2
2
拓展模型四 K字型(旋转+平移)
BD⊥DE,AB⊥AC,CE⊥DE,那么一定有∠B=∠CAE.
若两个三角形中再有一组对应边相等,则两个三角形全等.
归纳总结
能力提高二
9.如图9,点F、A、G、C、H在同一直线上,EF⊥FH,BG⊥FH,DH⊥FH,且AE⊥AB,
AE=AB,BC⊥CD,BC=CD,请按图中标注的数据计算实线所围成图形的面积S= .
△EFA≌△AGB
AF=BG=2
AG=EF=6
△BGC≌△CHD
GC=HD=4
BG=CH=2
S梯形EFHD=
×(EF+DH)×FH
= ×(6+4)×14=70
S梯形EFHD﹣S△EFA﹣S△ABC﹣S△DHC
=70﹣ ×6×2﹣ ×(6+4)×2﹣ ×4×2
=50.
图9
6
2
4
2
50
如图10,B是线段AC上一点,分别以AB、BC为边长,在线段AC的同一侧作两个等边三角形△ABD与△BCE,连接AE与CD,AE与CD的交点为H,
(1)AE与DC相等吗?说明理由;
(2)求∠AHD的度数.
典型例题
图10
H
F
G
(1)△ABE≌△DBC
H
如图10,B是线段AC上一点,分别以AB、BC为边长,在线段AC的同一侧作两个等边三角形△ABD与△BCE,连接AE与CD,AE与CD的交点为H,(1)AE与DC相等吗?说明理由;(2)求∠AHD的度数.
△ABE≌△DBC
H
F
G
∠AHD=60°
AE=DC
典型例题
∠BAE=∠BDC
∠DAH+∠ADH=∠DAB+∠ADB
F
G
(1)解:AE=DC.
理由如下:
∵△ABD和△BCE是等边三角形,
∴BA=BD,BE=BC,∠ABD=∠CBE=60°.
∴∠ABD+∠DBE=∠CBE+∠DBE.
即∠ABE=∠DBC.
在△ABE和△DBC中,
(2)∵△ABD和△BCE都是等边三角形,
∴∠DAB=∠ADB=60°.
∵△ABE≌△DBC,
∴∠BAE=∠BDC.
∴∠BDH+∠DAH=∠BAE+∠DAH=∠DAB=60°.
∴在△AHD中,
∠AHD=180°﹣∠ADH﹣∠DAH
=180°﹣∠ADB﹣∠BDH﹣∠DAH
=180°﹣∠ADB﹣(∠BDH+∠DAH)
=180°﹣60°﹣60°
=60°.
如图10,B是线段AC上一点,分别以AB、BC为边长,在线段AC的同一侧作两个等边三角形△ABD与△BCE,连接AE与CD,AE与CD的交点为H,(1)AE与DC相等吗?说明理由;(2)求∠AHD的度数.
典型例题
图10
∴△ABE≌△DBC(SAS).
∴AE=DC.
H
F
G
开放性问题
上面问题中,你还能得出那些结论?
H
△ABF≌△DBG
AF=DG
H
△CBG≌△EBF
BG=BF
H
F
G
△BFG是等边三角形
FG∥BC
拓展模型五 手拉手型(旋转)
下列图形都是由两个等顶角的等腰三角形所组成,并且顶角的顶点为公共顶点.顶点相连的四条边,形象的可以看作两双手,所以通常称为手拉手模型.
归纳总结
H
C
A
B
E
D
F
G
O
能力提高三
10.(1)如图11,已知以△ABC的边AB、AC分别向外作等腰直角△ABD与等腰直角△ACE,
∠BAD=∠CAE=90°,连接BE和CD相交于点O,AB交CD于点F,AC交BE于点G,
请说明:BE=DC,且BE⊥DC.
(2)探究:如图12,若以△ABC的边AB、AC分别向外作等边△ABD与等边△ACE,连
接BE和CD相交于点O,AB交CD于点F,AC交BE于G,则BE与DC还相等吗?请说明
理由;并求出∠BOD的度数.
类比
10.(1)说明:∵△ABD和△ACE都是等腰直角三角形,
∴AB=AD,AE=AC.
又∵∠BAD=∠CAE=90°,
∴∠BAD+∠BAC=∠CAE+∠BAC.
即∠DAC=∠BAE.
在△ABE和△ADC中,
∴△ABE≌△ADC(SAS).
∴BE=DC.
∵△ABD和△ACE都是等腰直角三角形,
∴∠DBA=∠ADB=45°.
∵△ABE≌△ADC,
∴∠ABE=∠ADC.
∴∠ABE+∠BDF=∠ADC+∠BDF=∠ADB=45°.
∴在△BOD中,
∠BOD=180°﹣∠DBO﹣∠BDO
=180°﹣∠DBA﹣∠ABE﹣∠BDO
=180°﹣∠DBA﹣(∠ABE+∠BDF)
=180°﹣45°﹣45°
=90°.
∴BE⊥DC.
能力提高三
(2)解:BE=DC.
理由如下:
∵△ABD和△ACE是等边三角形,
∴AB=AD,AC=AE,∠BAD=∠CAE=60°.
∴∠BAD+∠BAC=∠CAE+∠BAC.
即∠BAE=∠DAC.
在△ABE和△ADC中,
∴△ABE≌△ADC(SAS).
∴BE=DC.
∵△ABD和△ACE都是等边三角形,
∴∠DBA=∠ADB=60°.
∵△ABE≌△ADC,
∴∠ABE=∠ADC.
∴∠ABE+∠BDO=∠ADC+∠BDO=∠ADB=60°,
∴在△BDO中,
∠BOD=180°﹣∠DBO﹣∠BDO
=180°﹣∠DBA﹣∠ABE﹣∠BDO
=180°﹣∠DBA﹣(∠ABE+∠BDO)
=180°﹣60°﹣60°
=60°.
能力提高三
手拉手型
等线段,共端点,关键是旋转
先找到两个全等三角形
探索变化问题中的不变性
归纳总结
课堂小结
一、8字形
K字型
手拉手型
二、平移型
对称型
旋转型
∠A+∠D=∠C+∠B
当堂检测
1.如图,OB、OC分别是∠ABC、∠ACB的角平分线,∠BOC=120°,则∠A=( )
2.如图,点O在AD上,∠A=∠C,∠AOC=∠BOD,AB=CD,AD=6,OB=2,则OC的长为( )
3.如图,△ACB和△DCE均为等腰三角形,点A、D、E在同一直线上,连接BE,
若∠CAB=∠CBA=∠CDE=∠CED=50°.(1)说明:AD=BE. (2)求∠AEB的度数.
A.2 B.3 C.4 D.6
A.40° B.60° C.110° D.120°
第1题图
第2题图
第3题图
3.(1)说明:∵∠CAB=∠CBA=∠CDE=∠CED=50°,
∴CA=CB,CD=CE,
∠ACB-∠BCD=∠DCE-∠BCD,
即∠ACD=∠BCE.
在△ACD和△BCE中,
(2)解:∵△ACD≌△BCE,
∴∠CDA=∠CEB,
∵∠CDE=∠CED=50°
∴∠CDA=180°-∠CDE=180°-50°=130°
∴∠CEB=130°
∴∠AEB=∠CEB-∠CEA=130°-50°=80°.
当堂检测答案
1. B 2. C
∴△ACD≌△BCE(SAS),
∴AD=BE.
作业
1.如图,在△ABC中,高BD、CF相交于点E,若∠A=52°,则∠BEC= °.
2.如图,AD是△ABC的中线,延长AD,过点B作BE⊥AD交AD的延长线于点E,过点C作CF⊥AD交AD
于点F.请说明:DE=DF.
3.如图①,B、C、E是同一直线上的三个点,四边形ABCD与四边形CEFG都是正方形.连接BG、DE.
(1)探究BG与DE之间的数量关系;
(2)当正方形CEFG绕点C在平面内顺时针转动到如图②所示位置时,线段BG和ED有何关系?说明理由.
第1题图
第2题图
第3题图
第四章 三角形复习课二
1.已知三角形的三边长分别为a、b、c,化简|a +b﹣c|﹣2|a﹣b﹣c|+|a+b+c|得( )
A.2a﹣2b﹣c B.4a﹣2c C.4b+2c D.2a﹣2b+c
2 .如图1,在△ABC中,AD平分∠BAC,EG⊥AD,且分别交AB、AD、
AC及BC的延长线于点E、H、F、G,若∠B=45°,∠ACB=75°,
则∠G的度数为( )
3.如图2,△ABC的三边的中线AD、BE、CF的公共点为G,且
AG:GD=2:1,若S△ABC=12,则图中阴影部分的面积是( )
A.6 B.5 C.4 D.3
A.15° B.22.5° C.27.5° D.30°
图1
图2
诊断练习一
4.如图3,已知线段AB、CD相交于点O,连接AD、CB,我们把形
如图3的图形称之为“8字形”.如图4,在图3的条件下,∠DAB
和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交
于点M、N,试解答下列问题:
(1)在图3中,求出∠A、∠B、∠C、∠D之间的数量关系;
(2)在图4中,若∠B=40°,∠D=36°,试求∠P的度数;
(3)如果图4中∠D和∠B为任意角时,其他条件不变,试问∠P
与∠D、∠B之间存在着怎样的数量关系.
图3
图4
能力提高一
解:∵△ABC的三边长a、b、c需满足两边之和大于第三边,两边之差小于第三边,
∴a+b﹣c>0,a﹣b﹣c<0,a+b+c>0.
∴|a+b﹣c|=a+b﹣c,|a﹣b﹣c|=b+c﹣a,|a+b+c|=a+b+c.
∴|a+b﹣c|﹣2|a﹣b﹣c|+|a+b+c|=(a+b﹣c)﹣2(b+c﹣a)+(a+b+c)=4a﹣2c.
1.已知三角形的三边长分别为a、b、c,化简|a +b﹣c|﹣2|a﹣b﹣c|+|a+b+c|得( )
A.2a﹣2b﹣c B.4a﹣2c C.4b+2c D.2a﹣2b+c
B
诊断练习一
图1
∴∠HAF+∠AFE=90°.
∴∠AFE=90°-∠HAF=60°.
∵∠AFE与∠GFC是对顶角,
∴∠GFC=∠AFE=60°.
∵∠ACB=75°,
∴∠ACG=180°-∠ACB=180°-75°=105°.
∵∠G+∠GFC+∠GCF=180°,
∴∠G=180°-∠GFC-∠GCF=180°-60°-105°=15°.
2 .如图1,在△ABC中,AD平分∠BAC,EG⊥AD,且分别交
AB、AD、AC及BC的延长线于点E、H、F、G,若∠B=45°,
∠ACB=75°,则∠G的度数为( )
A.15° B.22.5° C.27.5° D.30°
解:∵∠BAC+∠B+∠ACB=180°,
∴∠BAC=180°-∠B-∠ACB.
∵∠B=45°,∠ACB=75°,
∴∠BAC=60°.
∵AD平分∠BAC,
∴∠CAD= =30°.
∵EG⊥AD,
A
诊断练习一
3.如图2,△ABC的三边的中线AD、BE、CF的公共点为G,且AG:GD=2:1,若S△ABC=12,则图中阴影部分的面积是( )
A.6 B.5 C.4 D.3
图2
C
诊断练习一
图2
4.解:(1)在△AOD中,
∵∠A+∠D+∠AOD=180°,
∴∠A+∠D=180°-∠AOD.
在△BOC中,
∵∠C+∠B+∠BOC=180°,
∴∠C+∠B=180°-∠BOC .
∵∠AOD=∠BOC,
∴∠A+∠D=∠C+∠B.
(2) ∵∠OAD+∠D=∠OCB+∠B.
∵∠B=40°,∠D=36°,
∴∠OAD+36°=∠OCB+40°.
∴∠OAD﹣∠OCB=4°.
∵AP、CP分别是∠DAB和∠BCD的角平分线,
∴∠DAM= ∠OAD,∠PCM= ∠OCB.
,
又∵∠DAM+∠D=∠PCM+∠P,
∴∠P=∠DAM+∠D -∠PCM = (∠OAD -∠OCB)+∠D
= ×4°+36°=38°.
(3)根据“8字形”数量关系,
∠OAD +∠D=∠OCB +∠B,
∠DAM +∠D=∠PCM +∠P,
∴∠OCB -∠OAD=∠D -∠B,
∠PCM-∠DAM=∠D -∠P,
∵AP、CP分别是∠DAB和∠BCD的角平分线,
∴∠DAM= ∠OAD,∠PCM= ∠OCB,
∴∠PCM -∠DAM= (∠OCB -∠OAD)= (∠D -∠B).
即∠D -∠P= (∠D -∠B).
整理得,∠P= (∠B+∠D).
图3
图4
能力提高一
整体
思想
5.如图5,点E、C在线段BF上,BE=CF,AB=DE,AC=DF.请说明:∠ABC=∠DEF.
6.如图6,点E、F在BC上,BE=CF,AB=DC,∠B=∠C,请说明:AF=DE.
7.如图7,AB=AC,AB⊥AC,AD⊥AE,且∠ABD=∠ACE.请说明:BD=CE.
图5
图6
图7
诊断练习二
5.如图5,点E、C在线段BF上,BE=CF,AB=DE,AC=DF.请说明:∠ABC=∠DEF.
说明:∵BE=CF,
∴BE+EC=CF+EC.
∴BC=EF.
在△ABC和△DEF中,
∴△ABC≌△DEF(SSS).
∴∠ABC=∠DEF.
图5
诊断练习二
模型一 平移型
把△ABC沿着某个方向移动,得到的△DEF与△ ABC是平移型全等三角形.下图是常见的平移型全等三角形.
归纳总结
6.如图6,点E、F在BC上,BE=CF,AB=DC,∠B=∠C,请说明:AF=DE.
图6
说明:∵BE=CF,
∴BE+EF=CF+EF.
即BF=CE.
在△ABF和△DCE中,
∴△ABF≌△DCE(SAS).
∴AF=DE.
诊断练习二
模型二 对称型
将一个三角形沿着某一条直线翻折后,能够与另一个三角形完全重合,则这两个全等三角形是对称型全等三角形.此类图形中要注意其隐含条件,如公共边或公共角等.
归纳总结
说明∵AB⊥AC,AD⊥AE,
∴∠BAC=∠DAE=90°.
∴∠BAC-∠BAE=∠DAE-∠BAE.
即∠BAD=∠CAE.
在△ABD和△ACE中,
7.如图7,AB=AC,AB⊥AC,AD⊥AE,且∠ABD=∠ACE.请说明:BD=CE.
∴△ABD≌△ACE(ASA).
∴BD=CE.
图7
诊断练习二
模型三 旋转型
旋转一定角度后,两个三角形能够完全重合,则这两个三角形可称为旋转型全等三角形.识别旋转型全等三角形时,如左图,涉及对顶角相等;中间图,涉及等角加(减)公共角;右图,涉及公共边问题.
归纳总结
8.如图8,Rt△ABC中,∠BAC=90°,AB=AC,分别过点B、C作过点A的直线的垂线BD、CE,垂足分别为D、E,若BD=3,CE=2,求DE的长.
诊断练习二
图8
解:∵∠BAC=90°,
∴∠BAD+∠CAE=90°.
∵BD⊥DE,
∴∠D=90°.
∴∠BAD+∠ABD=90°.
∴∠ABD=∠CAE.
∴△BDA≌△AEC(AAS).
∴DA=EC=2,BD=AE=3.
∴DE=DA+AE=5.
∵CE⊥DE,
∴∠E=90°.
∴∠D=∠E.
在△BDA和△AEC中,
2
2
拓展模型四 K字型(旋转+平移)
BD⊥DE,AB⊥AC,CE⊥DE,那么一定有∠B=∠CAE.
若两个三角形中再有一组对应边相等,则两个三角形全等.
归纳总结
能力提高二
9.如图9,点F、A、G、C、H在同一直线上,EF⊥FH,BG⊥FH,DH⊥FH,且AE⊥AB,
AE=AB,BC⊥CD,BC=CD,请按图中标注的数据计算实线所围成图形的面积S= .
△EFA≌△AGB
AF=BG=2
AG=EF=6
△BGC≌△CHD
GC=HD=4
BG=CH=2
S梯形EFHD=
×(EF+DH)×FH
= ×(6+4)×14=70
S梯形EFHD﹣S△EFA﹣S△ABC﹣S△DHC
=70﹣ ×6×2﹣ ×(6+4)×2﹣ ×4×2
=50.
图9
6
2
4
2
50
如图10,B是线段AC上一点,分别以AB、BC为边长,在线段AC的同一侧作两个等边三角形△ABD与△BCE,连接AE与CD,AE与CD的交点为H,
(1)AE与DC相等吗?说明理由;
(2)求∠AHD的度数.
典型例题
图10
H
F
G
(1)△ABE≌△DBC
H
如图10,B是线段AC上一点,分别以AB、BC为边长,在线段AC的同一侧作两个等边三角形△ABD与△BCE,连接AE与CD,AE与CD的交点为H,(1)AE与DC相等吗?说明理由;(2)求∠AHD的度数.
△ABE≌△DBC
H
F
G
∠AHD=60°
AE=DC
典型例题
∠BAE=∠BDC
∠DAH+∠ADH=∠DAB+∠ADB
F
G
(1)解:AE=DC.
理由如下:
∵△ABD和△BCE是等边三角形,
∴BA=BD,BE=BC,∠ABD=∠CBE=60°.
∴∠ABD+∠DBE=∠CBE+∠DBE.
即∠ABE=∠DBC.
在△ABE和△DBC中,
(2)∵△ABD和△BCE都是等边三角形,
∴∠DAB=∠ADB=60°.
∵△ABE≌△DBC,
∴∠BAE=∠BDC.
∴∠BDH+∠DAH=∠BAE+∠DAH=∠DAB=60°.
∴在△AHD中,
∠AHD=180°﹣∠ADH﹣∠DAH
=180°﹣∠ADB﹣∠BDH﹣∠DAH
=180°﹣∠ADB﹣(∠BDH+∠DAH)
=180°﹣60°﹣60°
=60°.
如图10,B是线段AC上一点,分别以AB、BC为边长,在线段AC的同一侧作两个等边三角形△ABD与△BCE,连接AE与CD,AE与CD的交点为H,(1)AE与DC相等吗?说明理由;(2)求∠AHD的度数.
典型例题
图10
∴△ABE≌△DBC(SAS).
∴AE=DC.
H
F
G
开放性问题
上面问题中,你还能得出那些结论?
H
△ABF≌△DBG
AF=DG
H
△CBG≌△EBF
BG=BF
H
F
G
△BFG是等边三角形
FG∥BC
拓展模型五 手拉手型(旋转)
下列图形都是由两个等顶角的等腰三角形所组成,并且顶角的顶点为公共顶点.顶点相连的四条边,形象的可以看作两双手,所以通常称为手拉手模型.
归纳总结
H
C
A
B
E
D
F
G
O
能力提高三
10.(1)如图11,已知以△ABC的边AB、AC分别向外作等腰直角△ABD与等腰直角△ACE,
∠BAD=∠CAE=90°,连接BE和CD相交于点O,AB交CD于点F,AC交BE于点G,
请说明:BE=DC,且BE⊥DC.
(2)探究:如图12,若以△ABC的边AB、AC分别向外作等边△ABD与等边△ACE,连
接BE和CD相交于点O,AB交CD于点F,AC交BE于G,则BE与DC还相等吗?请说明
理由;并求出∠BOD的度数.
类比
10.(1)说明:∵△ABD和△ACE都是等腰直角三角形,
∴AB=AD,AE=AC.
又∵∠BAD=∠CAE=90°,
∴∠BAD+∠BAC=∠CAE+∠BAC.
即∠DAC=∠BAE.
在△ABE和△ADC中,
∴△ABE≌△ADC(SAS).
∴BE=DC.
∵△ABD和△ACE都是等腰直角三角形,
∴∠DBA=∠ADB=45°.
∵△ABE≌△ADC,
∴∠ABE=∠ADC.
∴∠ABE+∠BDF=∠ADC+∠BDF=∠ADB=45°.
∴在△BOD中,
∠BOD=180°﹣∠DBO﹣∠BDO
=180°﹣∠DBA﹣∠ABE﹣∠BDO
=180°﹣∠DBA﹣(∠ABE+∠BDF)
=180°﹣45°﹣45°
=90°.
∴BE⊥DC.
能力提高三
(2)解:BE=DC.
理由如下:
∵△ABD和△ACE是等边三角形,
∴AB=AD,AC=AE,∠BAD=∠CAE=60°.
∴∠BAD+∠BAC=∠CAE+∠BAC.
即∠BAE=∠DAC.
在△ABE和△ADC中,
∴△ABE≌△ADC(SAS).
∴BE=DC.
∵△ABD和△ACE都是等边三角形,
∴∠DBA=∠ADB=60°.
∵△ABE≌△ADC,
∴∠ABE=∠ADC.
∴∠ABE+∠BDO=∠ADC+∠BDO=∠ADB=60°,
∴在△BDO中,
∠BOD=180°﹣∠DBO﹣∠BDO
=180°﹣∠DBA﹣∠ABE﹣∠BDO
=180°﹣∠DBA﹣(∠ABE+∠BDO)
=180°﹣60°﹣60°
=60°.
能力提高三
手拉手型
等线段,共端点,关键是旋转
先找到两个全等三角形
探索变化问题中的不变性
归纳总结
课堂小结
一、8字形
K字型
手拉手型
二、平移型
对称型
旋转型
∠A+∠D=∠C+∠B
当堂检测
1.如图,OB、OC分别是∠ABC、∠ACB的角平分线,∠BOC=120°,则∠A=( )
2.如图,点O在AD上,∠A=∠C,∠AOC=∠BOD,AB=CD,AD=6,OB=2,则OC的长为( )
3.如图,△ACB和△DCE均为等腰三角形,点A、D、E在同一直线上,连接BE,
若∠CAB=∠CBA=∠CDE=∠CED=50°.(1)说明:AD=BE. (2)求∠AEB的度数.
A.2 B.3 C.4 D.6
A.40° B.60° C.110° D.120°
第1题图
第2题图
第3题图
3.(1)说明:∵∠CAB=∠CBA=∠CDE=∠CED=50°,
∴CA=CB,CD=CE,
∠ACB-∠BCD=∠DCE-∠BCD,
即∠ACD=∠BCE.
在△ACD和△BCE中,
(2)解:∵△ACD≌△BCE,
∴∠CDA=∠CEB,
∵∠CDE=∠CED=50°
∴∠CDA=180°-∠CDE=180°-50°=130°
∴∠CEB=130°
∴∠AEB=∠CEB-∠CEA=130°-50°=80°.
当堂检测答案
1. B 2. C
∴△ACD≌△BCE(SAS),
∴AD=BE.
作业
1.如图,在△ABC中,高BD、CF相交于点E,若∠A=52°,则∠BEC= °.
2.如图,AD是△ABC的中线,延长AD,过点B作BE⊥AD交AD的延长线于点E,过点C作CF⊥AD交AD
于点F.请说明:DE=DF.
3.如图①,B、C、E是同一直线上的三个点,四边形ABCD与四边形CEFG都是正方形.连接BG、DE.
(1)探究BG与DE之间的数量关系;
(2)当正方形CEFG绕点C在平面内顺时针转动到如图②所示位置时,线段BG和ED有何关系?说明理由.
第1题图
第2题图
第3题图
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
