青岛版数学九年级上4.1圆的对称性课件

(共12张PPT)
赵州石拱桥
1.1300多年前,我国隋朝建造的赵州石拱桥(如图)的桥拱是圆弧形,它的跨度(弧所对是弦的长)为 37.4 m,拱高(弧的中点到弦的距离,也叫弓形高)为7.2m,求桥拱的半径(精确到0.1m).
驶向胜利的彼岸
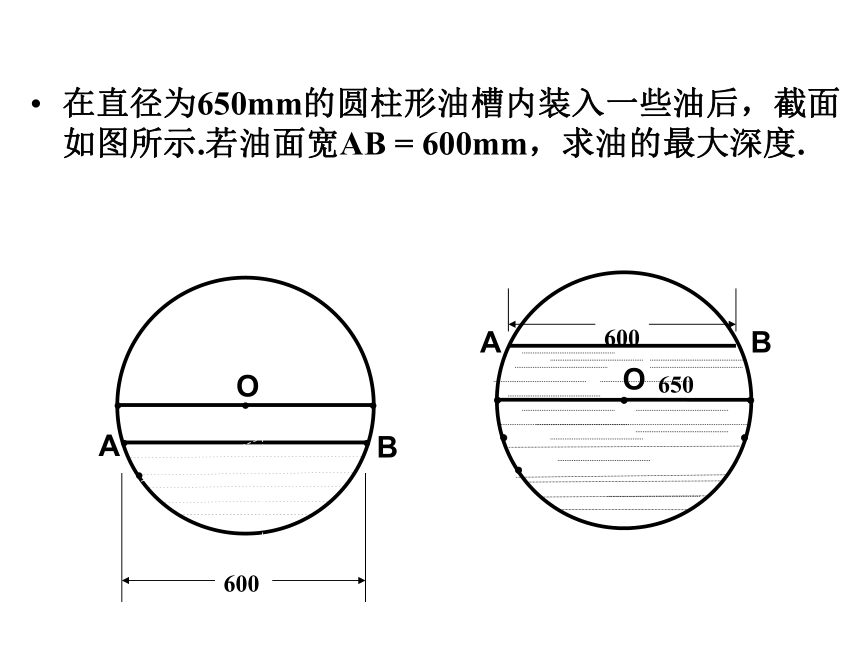
在直径为650mm的圆柱形油槽内装入一些油后，截面如图所示.若油面宽AB = 600mm，求油的最大深度.
D
┌
600
B
A
O
600
650
九年级数学第四章： 对圆的进一步认识
4.1圆的对称性
安丘市东埠中学 王苹
圆的对称性
圆是轴对称图形吗？
如果是,它的对称轴是什么 你能找到多少条对称轴？
●O
你是用什么方法解决上述问题的
●O
C
D
A
B
E└
⌒
⌒
AC与AD
⌒
⌒
BC与BD
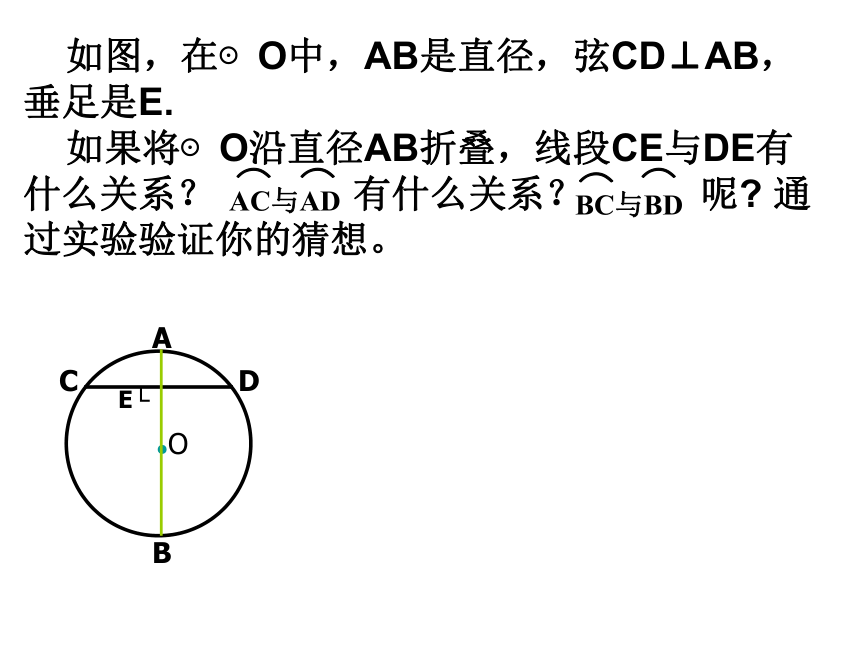
如图，在⊙O中，AB是直径，弦CD⊥AB，垂足是E.
如果将⊙O沿直径AB折叠，线段CE与DE有什么关系？ 有什么关系？ 呢 通过实验验证你的猜想。
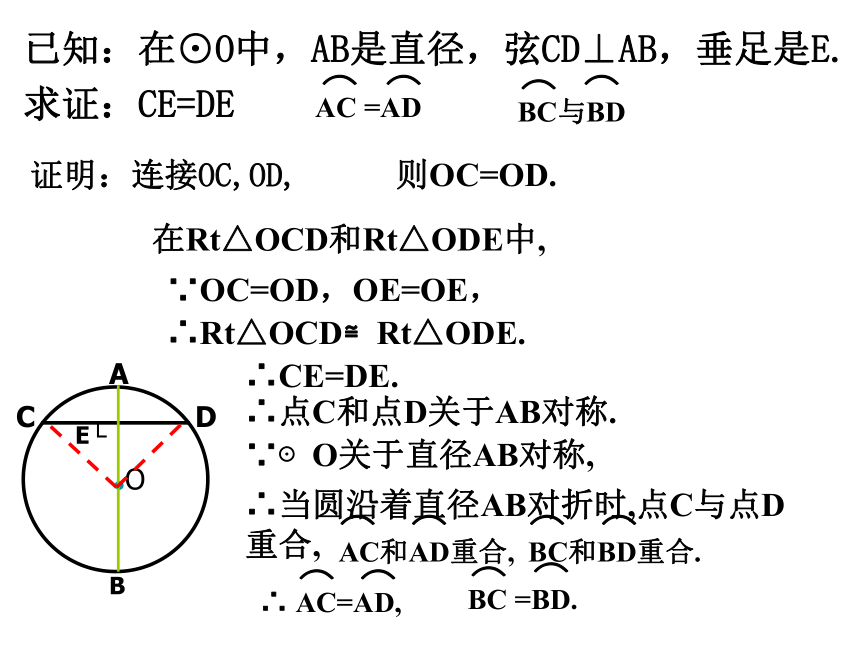
已知：在⊙O中，AB是直径，弦CD⊥AB，垂足是E.
求证：CE=DE
证明：连接OC,OD,
●O
C
D
A
B
E└
则OC=OD.
在Rt△OCD和Rt△ODE中,
∵OC=OD，OE=OE，
∴Rt△OCD≌Rt△ODE.
∴CE=DE.
∴点C和点D关于AB对称.
∵⊙O关于直径AB对称,
∴当圆沿着直径AB对折时,点C与点D重合,
⌒
⌒
AC和AD重合,
⌒
⌒
BC和BD重合.
⌒
⌒
∴ AC=AD,
⌒
⌒
　 BC =BD.
⌒
⌒
AC =AD
⌒
⌒
BC与BD
垂径定理
定理 垂直于弦的直径平分弦,并且平分弦所的两条弧.
提示:
垂径定理是圆中一个重要的结论,三种语言要相互转化，形成整体,才能运用自如.
驶向胜利的彼岸
●O
C
D
A
B
E└
AB⊥CD,
如图∵ AB是直径,
∴CE=DE,
⌒
⌒
AC =AD,
⌒
⌒
BC= BD.
知识升华：
垂径定理可以理解为一条直线，
具备两个条件：
①过圆心
②垂直于弦
就能得到三个结论：
①平分这条弦
②平分弦所对的优弧
③平分弦所对的劣弧
方法总结：
思考：在圆中解决与弦的有关问题时，经常作的辅助线是什么？
过圆心作弦的垂线段，连接半径，构造直角三角形，为应用垂径定理创作条件。
赵州石拱桥
1.1300多年前,我国隋朝建造的赵州石拱桥(如图)的桥拱是圆弧形,它的跨度(弧所对是弦的长)为 37.4 m,拱高(弧的中点到弦的距离,也叫弓形高)为7.2m,求桥拱的半径(精确到0.1m).
驶向胜利的彼岸
在直径为650mm的圆柱形油槽内装入一些油后，截面如图所示.若油面宽AB = 600mm，求油的最大深度.
D
┌
600
B
A
O
600
650
垂径定理的应用
在直径为650mm的圆柱形油槽内装入一些油后，截面如图所示.若油面宽AB = 600mm，求油的最大深度.
驶向胜利的彼岸
E
D
┌
600
B
A
O
600
650
D
C