青岛版数学九年级上4.1圆的对称性导学案
文档属性
| 名称 | 青岛版数学九年级上4.1圆的对称性导学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 32.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-25 00:00:00 | ||
图片预览

文档简介
4.1圆的对称性 导学案
一、学习目标:
1、了解圆的轴对称性。
2、探索并证明垂径定理,能用垂径定理解决有关问题。
学习重点:垂径定理及应用
难点:垂径定理的证明
二、知识链接:
1、圆是到 的距离等于 的点的集合。
2、连接圆上任意两点的线段叫做 ,圆中最长的弦是 。
3、圆上任意两点间的部分叫做 ,简称 ,直径分圆为两部分,每一部分叫做 ,大于半圆的弧叫做 ,小于半圆的弧叫做 ,
如图,弦AB把圆分成的劣弧是 ,优弧是 。
在同圆或等圆中能够互相重合的弧叫做 。
4、什么是轴对称图形?对称轴是条 (直线、射线、线段),
对称轴的性质是 对称点的连线。
三、新知探究:
(一) 交流发现:圆的轴对称性
1、圆是轴对称图形吗?
2、拿出准备好的半透明纸片,在纸上画一个圆,记作⊙O,任意作出一条直径,将⊙O沿直径折叠,你发现了什么结论?再任意作出一条直径,将⊙O沿这条直径折叠,是否发现有同样的结论?
3、总结概括:圆是 图形,对称轴是 。
对称轴有 条。
4、应用:一个圆形纸片,圆心没有标出,你能找到它的圆心吗?
(二)深入探究:垂径定理(重点、难点)
1、问题:
如图,在⊙O中,AB是直径,作弦CD⊥AB,垂足是E.如果将⊙O沿直径AB折叠,线段CE与DE有什么关系?与有什么关系?
与呢?通过实验验证你的猜想。
2、小组交流讨论,发现命题。
① 动手折叠,观察图形,你发现了什么结论,在组内交流讨论。
② 总结发现命题: 于弦的 , 这条弦,并且 弦所对的两条弧。
3、运用演绎推理,证明命题。
垂直于弦的直径,平分这条弦,并且平分弦所对的两条弧。
分析:命题的条件是 ,结论是 。
根据题意画出图形,写出已知,求证。你是怎么推理的,写出过程。
4、应用
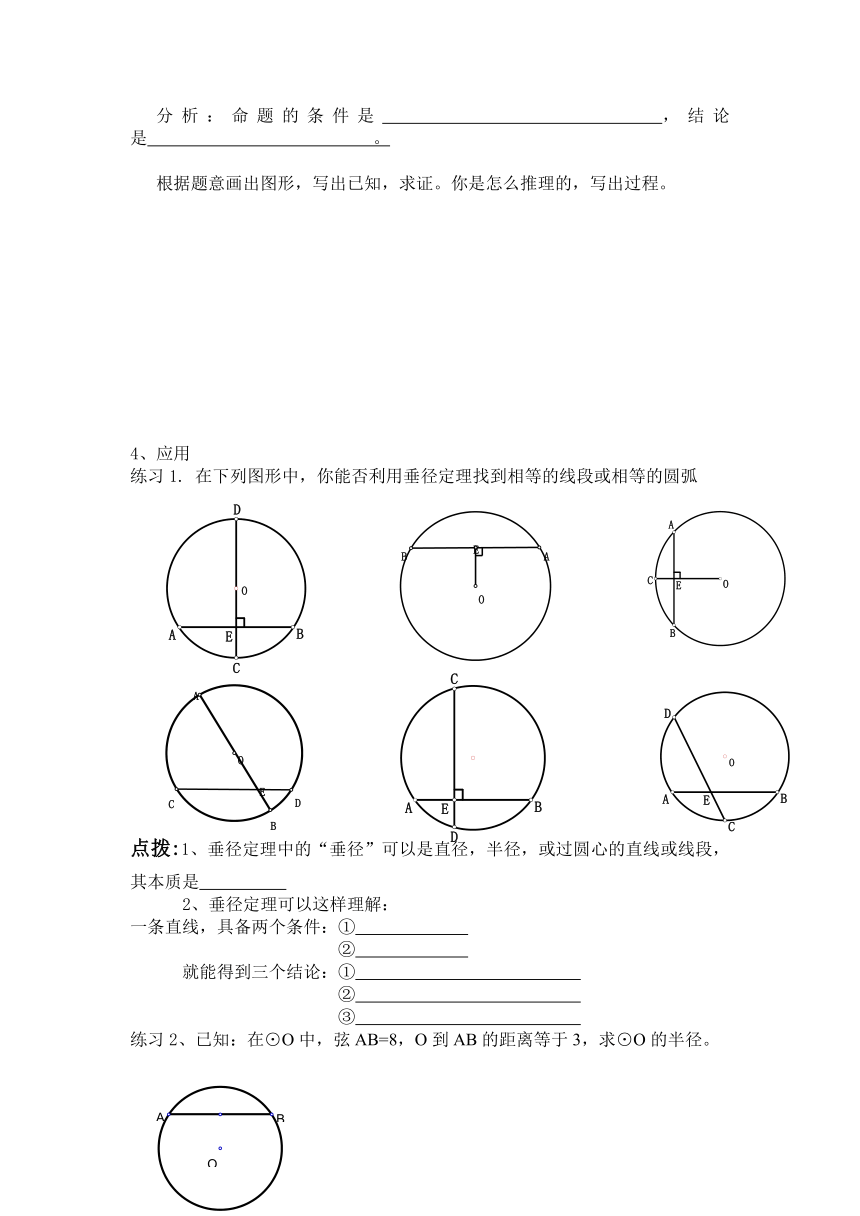
练习1. 在下列图形中,你能否利用垂径定理找到相等的线段或相等的圆弧
点拨:1、垂径定理中的“垂径”可以是直径,半径,或过圆心的直线或线段,其本质是
2、垂径定理可以这样理解:
一条直线,具备两个条件:①
②
就能得到三个结论:①
②
③
练习2、已知:在⊙O中,弦AB=8,O到AB的距离等于3,求⊙O的半径。
练习3、在⊙O中,弦AB=8厘米,OC⊥AB,CD=2cm,求⊙O的半径。
典例分析:自学课本109页例1,你能根据题意画出图形并给出解答吗?
思考:在圆中解决与弦有关问题时,经常作的辅助线是什么?
四、课堂小结:通过本节课的学习,你学到了什么,有哪些收获?
五、达标测试:
1已知:在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D两点
(1)若AB为直径, 求证: AC = BD
(2)若AB为不过圆心的弦,猜想AC 与 BD的大小关系,并证明。
2、如右图2所示,已知AB为⊙O的直径,且AB⊥CD,垂足为M,CD=8,AM=2,
则OM=_________.
六、课后提升:
1、⊙O的半径是5,P是圆内一点,且OP=3,过点P最长的弦长为 最短弦长为_________.
2、在⊙O中,弦AB∥CD,且AB = 8cm,CD = 6cm,⊙O的半径R = 5cm,求弦AB和CD的距离。
3、探究:垂径定理的推论
(1)如果CD是⊙O的弦(不是直径),过CD的中点E作⊙O的直径AB.
你发现AB与CD互相垂直吗?与有什么关系?与呢?通过实
验验证你的猜想。并给出证明。
(2)讨论: 如图,在下列五个条件中:
AB是直径, ② AB⊥CD, ③ CE=DE, ④AC=AD, ⑤BC=BD. 如果具备其中两个
条件,能否推出其余三个结论成立?
O
B
A
E
E
O
C
D
A
B
O
A
B
一、学习目标:
1、了解圆的轴对称性。
2、探索并证明垂径定理,能用垂径定理解决有关问题。
学习重点:垂径定理及应用
难点:垂径定理的证明
二、知识链接:
1、圆是到 的距离等于 的点的集合。
2、连接圆上任意两点的线段叫做 ,圆中最长的弦是 。
3、圆上任意两点间的部分叫做 ,简称 ,直径分圆为两部分,每一部分叫做 ,大于半圆的弧叫做 ,小于半圆的弧叫做 ,
如图,弦AB把圆分成的劣弧是 ,优弧是 。
在同圆或等圆中能够互相重合的弧叫做 。
4、什么是轴对称图形?对称轴是条 (直线、射线、线段),
对称轴的性质是 对称点的连线。
三、新知探究:
(一) 交流发现:圆的轴对称性
1、圆是轴对称图形吗?
2、拿出准备好的半透明纸片,在纸上画一个圆,记作⊙O,任意作出一条直径,将⊙O沿直径折叠,你发现了什么结论?再任意作出一条直径,将⊙O沿这条直径折叠,是否发现有同样的结论?
3、总结概括:圆是 图形,对称轴是 。
对称轴有 条。
4、应用:一个圆形纸片,圆心没有标出,你能找到它的圆心吗?
(二)深入探究:垂径定理(重点、难点)
1、问题:
如图,在⊙O中,AB是直径,作弦CD⊥AB,垂足是E.如果将⊙O沿直径AB折叠,线段CE与DE有什么关系?与有什么关系?
与呢?通过实验验证你的猜想。
2、小组交流讨论,发现命题。
① 动手折叠,观察图形,你发现了什么结论,在组内交流讨论。
② 总结发现命题: 于弦的 , 这条弦,并且 弦所对的两条弧。
3、运用演绎推理,证明命题。
垂直于弦的直径,平分这条弦,并且平分弦所对的两条弧。
分析:命题的条件是 ,结论是 。
根据题意画出图形,写出已知,求证。你是怎么推理的,写出过程。
4、应用
练习1. 在下列图形中,你能否利用垂径定理找到相等的线段或相等的圆弧
点拨:1、垂径定理中的“垂径”可以是直径,半径,或过圆心的直线或线段,其本质是
2、垂径定理可以这样理解:
一条直线,具备两个条件:①
②
就能得到三个结论:①
②
③
练习2、已知:在⊙O中,弦AB=8,O到AB的距离等于3,求⊙O的半径。
练习3、在⊙O中,弦AB=8厘米,OC⊥AB,CD=2cm,求⊙O的半径。
典例分析:自学课本109页例1,你能根据题意画出图形并给出解答吗?
思考:在圆中解决与弦有关问题时,经常作的辅助线是什么?
四、课堂小结:通过本节课的学习,你学到了什么,有哪些收获?
五、达标测试:
1已知:在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D两点
(1)若AB为直径, 求证: AC = BD
(2)若AB为不过圆心的弦,猜想AC 与 BD的大小关系,并证明。
2、如右图2所示,已知AB为⊙O的直径,且AB⊥CD,垂足为M,CD=8,AM=2,
则OM=_________.
六、课后提升:
1、⊙O的半径是5,P是圆内一点,且OP=3,过点P最长的弦长为 最短弦长为_________.
2、在⊙O中,弦AB∥CD,且AB = 8cm,CD = 6cm,⊙O的半径R = 5cm,求弦AB和CD的距离。
3、探究:垂径定理的推论
(1)如果CD是⊙O的弦(不是直径),过CD的中点E作⊙O的直径AB.
你发现AB与CD互相垂直吗?与有什么关系?与呢?通过实
验验证你的猜想。并给出证明。
(2)讨论: 如图,在下列五个条件中:
AB是直径, ② AB⊥CD, ③ CE=DE, ④AC=AD, ⑤BC=BD. 如果具备其中两个
条件,能否推出其余三个结论成立?
O
B
A
E
E
O
C
D
A
B
O
A
B
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
