北师大版九年级数学下册 第3章 《圆》压轴题型提升训练(二)(Word版 含解析)
文档属性
| 名称 | 北师大版九年级数学下册 第3章 《圆》压轴题型提升训练(二)(Word版 含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 238.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 00:00:00 | ||
图片预览



文档简介
九年级数学下册
第3章
《圆》
压轴题型提升训练(二)
1.如图1,AB是⊙O的直径,C是⊙O上一点,CD⊥AB于D,E是BA延长线上一点,连接CE,∠ACE=∠ACD,K是线段AO上一点,连接CK并延长交⊙O于点F.
(1)求证:CE是⊙O的切线;
(2)若AD=DK,求证:AK?AO=KB?AE;
(3)如图2,若AE=AK,=,点G是BC的中点,AG与CF交于点P,连接BP.请猜想PA,PB,PF的数量关系,并证明.
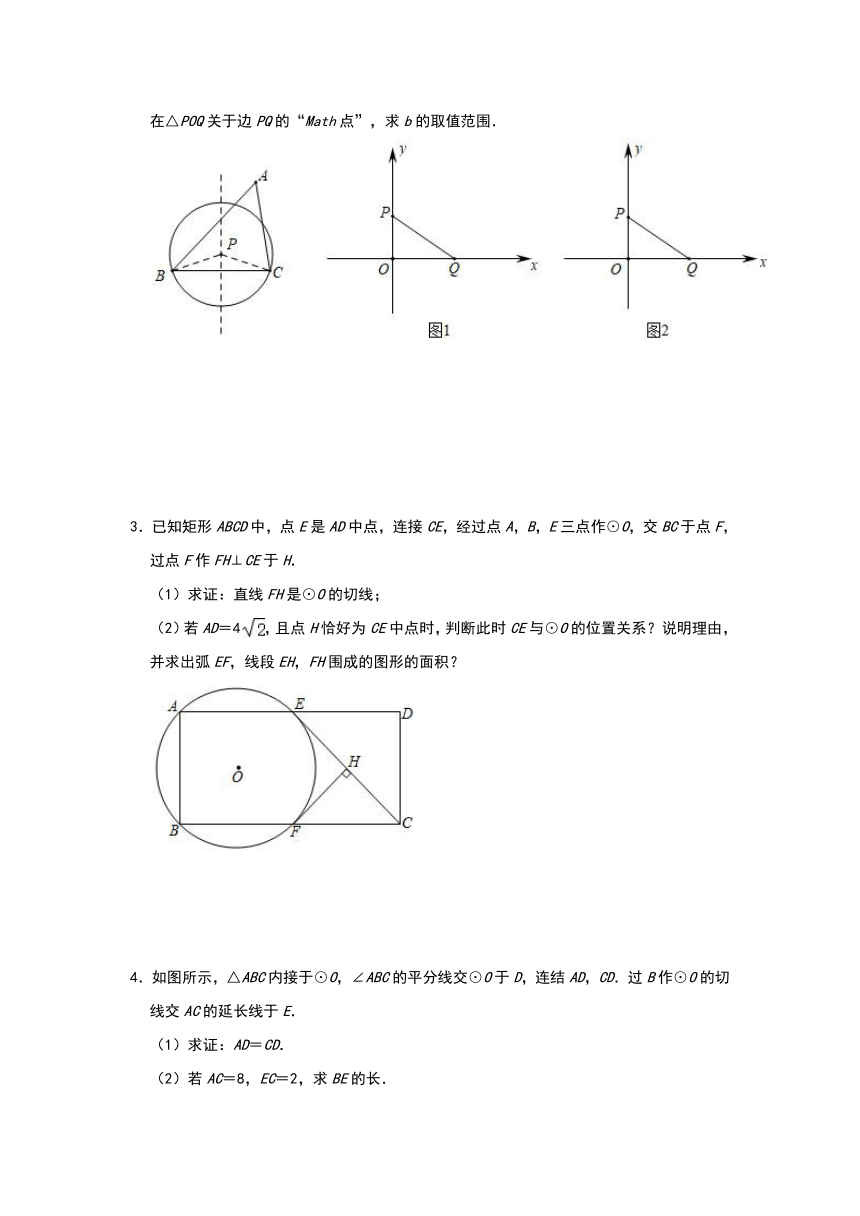
2.在平面直角坐标系xOy中,对于△ABC,点P在BC边的垂直平分线上,若以点P为圆心,PB为半径的?P与△ABC三条边的公共点个数之和不小于3,则称点P为△ABC关于边BC的“Math点”.如图所示,点P即为△ABC关于边BC的“Math点”.已知点P(0,4),Q(a,0).
(1)如图1,a=4,在点A(1,0)、B(2,2)、C(,)、D(5,5)中,△POQ关于边PQ的“Math点”为
.
(2)如图2,,
①已知D(0,8),点E为△POQ关于边PQ的“Math点”,请直接写出线段DE的长度的取值范围;
②将△POQ绕原点O旋转一周,直线交x轴、y轴于点M、N,若线段MN上存在△POQ关于边PQ的“Math点”,求b的取值范围.
3.已知矩形ABCD中,点E是AD中点,连接CE,经过点A,B,E三点作⊙O,交BC于点F,过点F作FH⊥CE于H.
(1)求证:直线FH是⊙O的切线;
(2)若AD=4,且点H恰好为CE中点时,判断此时CE与⊙O的位置关系?说明理由,并求出弧EF,线段EH,FH围成的图形的面积?
4.如图所示,△ABC内接于⊙O,∠ABC的平分线交⊙O于D,连结AD,CD.过B作⊙O的切线交AC的延长线于E.
(1)求证:AD=CD.
(2)若AC=8,EC=2,求BE的长.
(3)若AB,BC(AB>BC)的长是一元二次方程x2﹣14x+48=0的两根,若∠ADC=90°,直接写出AC及BD的长.
5.如图,△EBF中,∠B=90°,O是BE上一点,以O为圆心,OB为半径的圆与OF交于点C,与EB交于点A,与EF交于点D,连接AD、DC,四边形AOCD为平行四边形.
(1)求证:EF为⊙O的切线;
(2)已知⊙O的半径为1,求图中阴影部分的面积.
6.如图,AB是⊙O的一条弦,OD⊥AB,垂足为C,OD交⊙O于点D,点E在⊙O上,若∠AOD=50°.
(1)求∠DEB的度数;
(2)若OC=3,OA=5,
①求弦AB的长;
②求劣弧AB的长.
7.我们知道:有一内角为直角的三角形叫做直角三角形.类似地,我们定义:有一内角为45°的三角形叫做半直角三角形.如图,在平面直角坐标系中,O为原点,A(4,0),B(﹣4,0),D是y轴上的一个动点,∠ADC=90°(A、D、C按顺时针方向排列),BC与经过A、B、D三点的⊙M交于点E,DE平分∠ADC,连结AE,BD.显然△DCE、△DEF、△DAE是半直角三角形.
(1)求证:△ABC是半直角三角形;
(2)求证:∠DEC=∠DEA;
(3)若点D的坐标为(0,8),求AE的长.
8.如图,在⊙O中,AB是⊙O的直径,点C在⊙O上,OD⊥AC于点D,延长DO交⊙O于点E,连接EC、EB、BC,若AC=6,OD=.
(1)求⊙O的直径;
(2)求△BEC的面积.
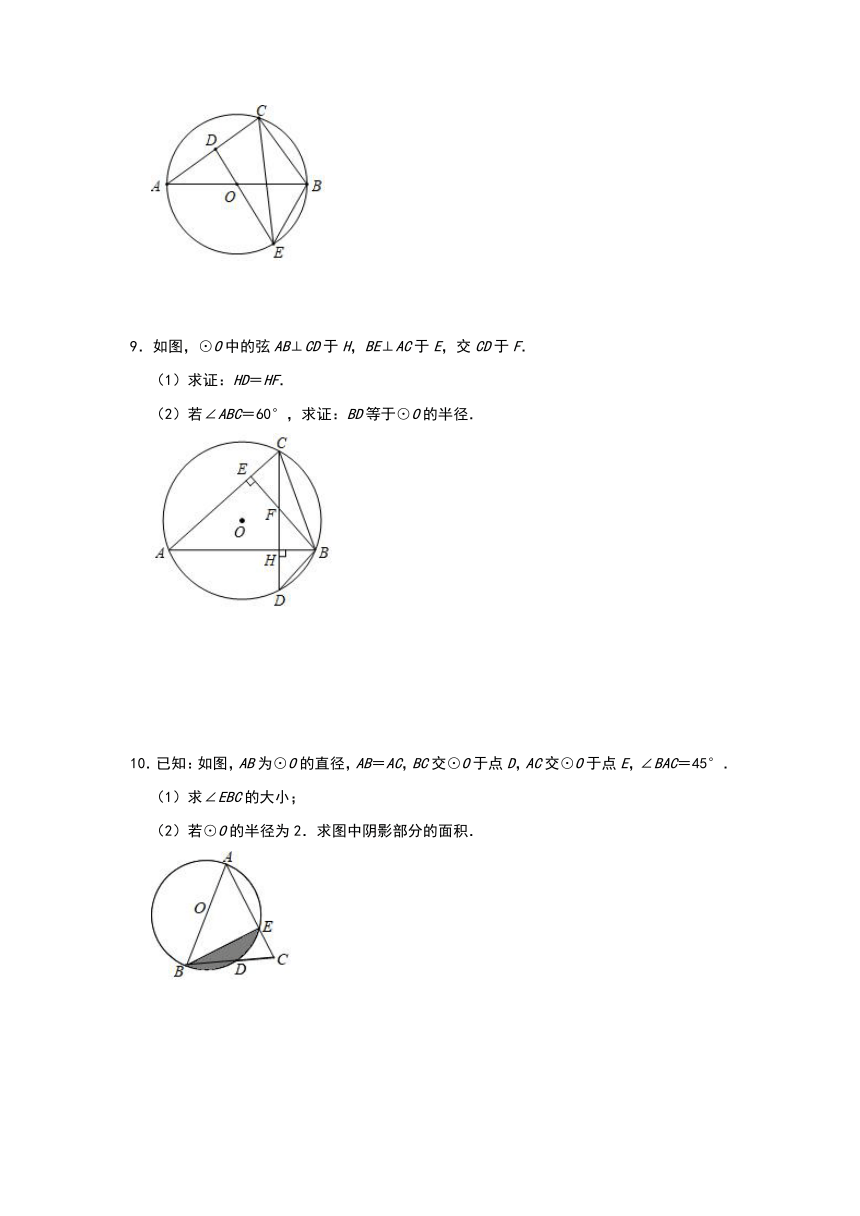
9.如图,⊙O中的弦AB⊥CD于H,BE⊥AC于E,交CD于F.
(1)求证:HD=HF.
(2)若∠ABC=60°,求证:BD等于⊙O的半径.
10.已知:如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°.
(1)求∠EBC的大小;
(2)若⊙O的半径为2.求图中阴影部分的面积.
参考答案
1.解:(1)证明:连接OC,如图所示:
∵CD⊥AB,
∴∠CAD+∠ACD=90°,
∵OA=OC,
∴∠CAD=∠ACO,
又∵∠ACE=∠ACD,
∴∠ACE+∠ACO=90°,即∠ECO=90°,
∴CE是⊙O的切线;
(2)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠CAD+∠B=90°,
又∵∠CAD+∠ACD=90°,∠ACD=∠B,
∴∠ACE=∠B,
∵AD=DK,CD⊥AB,
∴CA=CK,∠CAD=∠CKD,
∴∠CAE=∠BKC,
∴△CAE∽△BKC,
∴=,
∴AC?KC=AE?KB,
又∵∠CAD=∠CKD,∠CAD=∠OCA,
∴△OCA∽△CAK,
∴=,
∴AC?KC=AK?AO,
∴AK?AO=KB?AE;
(3)PA2+PF2=PB2.理由如下:
如图,连接AF、BF,
∵=,
∴∠ACF=∠BCF=∠ACB=45°,AF=BF,
∴∠ECK=∠ACK+∠ACE=45°+∠ACE,∠EKC=∠BCK+∠KBC=45°+∠ABC,
∴∠ECK=∠EKC,
∴EC=EK=AE+EK=2AE,
∵∠ACE=∠CBE,∠E=∠E,
∴△EAC∽△ECB,
∴==,
∴BC=2AC,
∵点G是BC的中点,
∴BC=2CG=2GB,
∴AC=CG,∠ACF=∠BCF,
∴CP⊥AG,AP=PG,
设AC=CG=GB=x,
则AG==x,
∴==,
又∠PGB=∠BGA,
∴△PGB∽△BGA,
∴∠GBP=∠GAB,
∴∠GBP+∠BCF=∠GAB+∠GAC,
即∠BPF=∠BAC=∠BFP,
∴BP=BF=AF,
∵在Rt△APF中,PA2+PF2=AF2,
∴PA2+PF2=PB2.
2.解:(1)根据“Math点”的定义,观察图象可知,△POQ关于边PQ的“Math点”为B、C.
故答案为:B,C.
(2)如图2中,∵P(0,4),Q(4,0),
∴OP=4,OQ=4,
∴tan∠PQO=,
∴∠PQO=30°,
①当点E与PQ的中点K重合时,点E是△POQ关于边PQ的“Math点”,此时E(2,2),
∵D(0,8),
∴DE==4,
当⊙E′与x轴相切于点Q时,E′(4,8),
∴DE′=4,
观察图象可知,当点E在线段KE′上时,点E为△POQ关于边PQ的“Math点”,
∵E′Q⊥OQ,
∴∠E′QO=90°,
∴∠E′QK=60°,
∴∠E′KQ=90°,
∴∠EE′Q=30°,
∵DE′∥OQ,
∴∠DE′K=60°,
∵DE′=DK,
∴△DE′K是等边三角形,
∵点D到E′K的距离的最小值为4?sin60°=6,
∴.
②如图3中,分别以O为圆心,2和4为半径画圆,
当线段MN与图中圆环有交点时,线段MN上存在△POQ关于边PQ的“Math点”,
当直线MN与小圆相切时,b=±4,
当直线MN与大圆相切时,b=±8,
观察图象可知,满足条件的b的值为:或.
3.解:(1)连接BE,OF,
∵四边形ABCD是矩形,
∴∠A=∠D=90°,AB=CD,
∵∠A=90°,
∴BE是⊙O的直径,
∵点E是AD的中点,
∴EA=ED,
∴△EAB≌△EDC
(SAS),
∴EB=EC,
∴∠EBC=∠ECB,
∵OB=OF,
∴∠EBC=∠OFB,
∴∠ECB=∠OFB,
∴OF∥EC,
∴∠OFH=∠FHC,
∵FH⊥CE,
∴∠FHC=∠OFH=90°,
又∵OF是⊙O的半径,
∴直线FH是⊙O的切线;
(2)EC与⊙O相切,
理由:连接EF,
由(1)得,BE是⊙O的直径,
∴∠EFB=EFC=90°,
∵点H是EC的中点,
∴FH=EH=HC,
∵FH⊥CE,
∴∠FHC=90°,
∴∠ECF=∠HFC=45°,
∵EB=EC,
∴∠EBF=∠ECF=45°,
∴∠BEC=90°,
又∵OE是⊙O的半径,
∴直线EC是⊙O的切线;
由上述可知,四边形ABFE和四边形OFHE都是正方形,
∴AE=AB=AD=×4=2,
∴BE==4,
∴OE=OF=2,
∴S=S正方形OFHE﹣S扇形OEF=22﹣=4﹣π.
4.解:(1)∵BD为∠ABC的角平分线,
∴∠ABD=∠CBD,
∴AD=CD;
(2)连接BO并延长交⊙O于点F,连接CF,则BF为直径,即∠BCF=90°,
又∵BE为⊙O切线,
∴OB⊥BE,即∠OBE=90°=∠BCF,
∴∠EBC+∠FBC=∠FBC+∠F,
∴∠EBC=∠F,
又∵∠F=∠BAC,
∴∠EBC=∠BAC,
又∵CE=CE,
∴△EBC∽△EAB,
∴,
∴BE2=AE?EC=(EC+AC)?EC,
即BE2=10×2,
∴(负值已舍去),
(3)∵x2﹣14x+48=0,(x﹣8)(x﹣6)=0,
∴x1=8,x2=6,
又∵AB>BC,
∴AB=8,BC=6,
又∵∠ABC=180°﹣∠ADC=90°,
∴由勾股定理:,
过A作AH⊥BD交BD于H,
∵∠ADC=90°,AD=DC,
∴,
∴,
又∵∠ABD=∠ACD=45°,
∴,
在Rt△AHD中,
由勾股定理:,
∴.
5.(1)证明:连接OD,如图所示:
∵四边形AOCD为平行四边形,
∴OA=DC,OC=AD,
∵OA=OC=OD,
∴OA=OD=AD,DC=OC=OD,
∴△OAD、△OCD都是等边三角形,
∴∠AOD=∠COD=60°,
∴∠BOC=180°﹣∠AOD﹣∠COD=60°,
在△OBF和△ODF中,
,
∴△OBF≌△ODF(SAS),
∴∠OBF=∠ODF,
∵∠OBF=90°,
∴∠ODF=90°,
∴EF⊥OD
∵点D在⊙O上,
∴EF为⊙O的切线;
(2)解:在Rt△ODE中,∵∠AOD=60°,
∴∠FEB=30°,
∵OD=1,
∴OE=2,DE=OD=,
∴S△EOD=OD×DE=×1×=,S扇形AOD==π,
∴图中阴影部分的面积=S△EOD﹣S扇形AOD=﹣π.
6.解:(1)∵OD⊥AB,
∴=,
∴∠DEB=∠AOD=×50°=25°.
(2)①∵OC=3,OA=5,
∴AC=4,
∵OD⊥AB,
∴==,
∴AC=BC=AB=4,
∴AB=8;
②∵∠AOD=50°,=,
∴∠AOB=100°,
∵OA=5,
∴的长===.
7.(1)证明:∵∠ADC=90°,DE平分∠ADC,
∴∠ADE=45°,
∵∠ABE=∠ADE=45°,
∴△ABC是半直角三角形;
(2)证明:∵OM⊥AB,OA=OB,
∴AD=BD,
∴∠DAB=∠DBA,
∵∠DEB=∠DAB,
∴∠DBA=∠DEB,
∵D、B、A、E四点共圆,
∴∠DBA+∠DEA=180°,
∵∠DEB+∠DEC=180°,
∴∠DEA=∠DEC;
(3)解:如图1,连接AM,ME,设⊙M的半径为r,
∵点D的坐标为(0,8),
∴OM=8﹣r,
由OM2+OA2=MA2得:(8﹣r)2+42=r2,
解得r=5,
∴⊙M
的半径为5,
∵∠ABE=45°,
∴∠EMA=2∠ABE=90°,
∴EA2=MA2+ME2=52+52=50,
∴AE=5.
8.解:(1)∵OD⊥AC,AC=6,
∴AD=3,
∵OD=,
∴OA=4,
∴⊙O的直径=8;
(2)过点E作EF⊥CB,交CB的延长线于点F,
∵AB为直径,
∴∠ACB=∠CDE=∠CFE=90°,
∴四边形CDEF为矩形,
∴EF=CD=AC=3,BC===2,
∴S△BEC=×BC×EF=×3=3.
9.证明:(1)∵CH⊥AB,
∴∠BFH+∠FBH=90°,
∵BE⊥AC,
∴∠A+∠ABE=90°,
∴∠BFH=∠A,
∵∠A=∠D,
∴∠BFH=∠D,
∴BF=BD,
∵BH⊥FD,
∴HD=HF;
(2)连接OD、OB,如图,
∵∠BCD+∠CBH=90°,
∴∠BCH=90°﹣∠CBH=90°﹣60°=30°,
∴∠BOD=2∠BCD=60°,
∵OB=OD,
∴△OBD为等边三角形,
∴BD=OB,
∴BD等于⊙O的半径.
10.解;(1)∵AB是⊙O的直径,
∴∠AEB=90°,
又∵∠BAC=45°,
∴∠ABE=45°.
又∵AB=AC,
∴∠ABC=∠C=67.5°.
∴∠EBC=22.5°;
(2)连接OE,
∵AB是⊙O的直径,
∴∠AEB=90°,
又∵∠BAC=45°,
∴∠ABE=45°.
∴AE=BE,
∵OA=OB,
∴OE⊥AB,
∵OA=OB=OE=2,
∴S阴影=S扇形OBE﹣S△OBE=﹣=﹣=π﹣2.
第3章
《圆》
压轴题型提升训练(二)
1.如图1,AB是⊙O的直径,C是⊙O上一点,CD⊥AB于D,E是BA延长线上一点,连接CE,∠ACE=∠ACD,K是线段AO上一点,连接CK并延长交⊙O于点F.
(1)求证:CE是⊙O的切线;
(2)若AD=DK,求证:AK?AO=KB?AE;
(3)如图2,若AE=AK,=,点G是BC的中点,AG与CF交于点P,连接BP.请猜想PA,PB,PF的数量关系,并证明.
2.在平面直角坐标系xOy中,对于△ABC,点P在BC边的垂直平分线上,若以点P为圆心,PB为半径的?P与△ABC三条边的公共点个数之和不小于3,则称点P为△ABC关于边BC的“Math点”.如图所示,点P即为△ABC关于边BC的“Math点”.已知点P(0,4),Q(a,0).
(1)如图1,a=4,在点A(1,0)、B(2,2)、C(,)、D(5,5)中,△POQ关于边PQ的“Math点”为
.
(2)如图2,,
①已知D(0,8),点E为△POQ关于边PQ的“Math点”,请直接写出线段DE的长度的取值范围;
②将△POQ绕原点O旋转一周,直线交x轴、y轴于点M、N,若线段MN上存在△POQ关于边PQ的“Math点”,求b的取值范围.
3.已知矩形ABCD中,点E是AD中点,连接CE,经过点A,B,E三点作⊙O,交BC于点F,过点F作FH⊥CE于H.
(1)求证:直线FH是⊙O的切线;
(2)若AD=4,且点H恰好为CE中点时,判断此时CE与⊙O的位置关系?说明理由,并求出弧EF,线段EH,FH围成的图形的面积?
4.如图所示,△ABC内接于⊙O,∠ABC的平分线交⊙O于D,连结AD,CD.过B作⊙O的切线交AC的延长线于E.
(1)求证:AD=CD.
(2)若AC=8,EC=2,求BE的长.
(3)若AB,BC(AB>BC)的长是一元二次方程x2﹣14x+48=0的两根,若∠ADC=90°,直接写出AC及BD的长.
5.如图,△EBF中,∠B=90°,O是BE上一点,以O为圆心,OB为半径的圆与OF交于点C,与EB交于点A,与EF交于点D,连接AD、DC,四边形AOCD为平行四边形.
(1)求证:EF为⊙O的切线;
(2)已知⊙O的半径为1,求图中阴影部分的面积.
6.如图,AB是⊙O的一条弦,OD⊥AB,垂足为C,OD交⊙O于点D,点E在⊙O上,若∠AOD=50°.
(1)求∠DEB的度数;
(2)若OC=3,OA=5,
①求弦AB的长;
②求劣弧AB的长.
7.我们知道:有一内角为直角的三角形叫做直角三角形.类似地,我们定义:有一内角为45°的三角形叫做半直角三角形.如图,在平面直角坐标系中,O为原点,A(4,0),B(﹣4,0),D是y轴上的一个动点,∠ADC=90°(A、D、C按顺时针方向排列),BC与经过A、B、D三点的⊙M交于点E,DE平分∠ADC,连结AE,BD.显然△DCE、△DEF、△DAE是半直角三角形.
(1)求证:△ABC是半直角三角形;
(2)求证:∠DEC=∠DEA;
(3)若点D的坐标为(0,8),求AE的长.
8.如图,在⊙O中,AB是⊙O的直径,点C在⊙O上,OD⊥AC于点D,延长DO交⊙O于点E,连接EC、EB、BC,若AC=6,OD=.
(1)求⊙O的直径;
(2)求△BEC的面积.
9.如图,⊙O中的弦AB⊥CD于H,BE⊥AC于E,交CD于F.
(1)求证:HD=HF.
(2)若∠ABC=60°,求证:BD等于⊙O的半径.
10.已知:如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°.
(1)求∠EBC的大小;
(2)若⊙O的半径为2.求图中阴影部分的面积.
参考答案
1.解:(1)证明:连接OC,如图所示:
∵CD⊥AB,
∴∠CAD+∠ACD=90°,
∵OA=OC,
∴∠CAD=∠ACO,
又∵∠ACE=∠ACD,
∴∠ACE+∠ACO=90°,即∠ECO=90°,
∴CE是⊙O的切线;
(2)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠CAD+∠B=90°,
又∵∠CAD+∠ACD=90°,∠ACD=∠B,
∴∠ACE=∠B,
∵AD=DK,CD⊥AB,
∴CA=CK,∠CAD=∠CKD,
∴∠CAE=∠BKC,
∴△CAE∽△BKC,
∴=,
∴AC?KC=AE?KB,
又∵∠CAD=∠CKD,∠CAD=∠OCA,
∴△OCA∽△CAK,
∴=,
∴AC?KC=AK?AO,
∴AK?AO=KB?AE;
(3)PA2+PF2=PB2.理由如下:
如图,连接AF、BF,
∵=,
∴∠ACF=∠BCF=∠ACB=45°,AF=BF,
∴∠ECK=∠ACK+∠ACE=45°+∠ACE,∠EKC=∠BCK+∠KBC=45°+∠ABC,
∴∠ECK=∠EKC,
∴EC=EK=AE+EK=2AE,
∵∠ACE=∠CBE,∠E=∠E,
∴△EAC∽△ECB,
∴==,
∴BC=2AC,
∵点G是BC的中点,
∴BC=2CG=2GB,
∴AC=CG,∠ACF=∠BCF,
∴CP⊥AG,AP=PG,
设AC=CG=GB=x,
则AG==x,
∴==,
又∠PGB=∠BGA,
∴△PGB∽△BGA,
∴∠GBP=∠GAB,
∴∠GBP+∠BCF=∠GAB+∠GAC,
即∠BPF=∠BAC=∠BFP,
∴BP=BF=AF,
∵在Rt△APF中,PA2+PF2=AF2,
∴PA2+PF2=PB2.
2.解:(1)根据“Math点”的定义,观察图象可知,△POQ关于边PQ的“Math点”为B、C.
故答案为:B,C.
(2)如图2中,∵P(0,4),Q(4,0),
∴OP=4,OQ=4,
∴tan∠PQO=,
∴∠PQO=30°,
①当点E与PQ的中点K重合时,点E是△POQ关于边PQ的“Math点”,此时E(2,2),
∵D(0,8),
∴DE==4,
当⊙E′与x轴相切于点Q时,E′(4,8),
∴DE′=4,
观察图象可知,当点E在线段KE′上时,点E为△POQ关于边PQ的“Math点”,
∵E′Q⊥OQ,
∴∠E′QO=90°,
∴∠E′QK=60°,
∴∠E′KQ=90°,
∴∠EE′Q=30°,
∵DE′∥OQ,
∴∠DE′K=60°,
∵DE′=DK,
∴△DE′K是等边三角形,
∵点D到E′K的距离的最小值为4?sin60°=6,
∴.
②如图3中,分别以O为圆心,2和4为半径画圆,
当线段MN与图中圆环有交点时,线段MN上存在△POQ关于边PQ的“Math点”,
当直线MN与小圆相切时,b=±4,
当直线MN与大圆相切时,b=±8,
观察图象可知,满足条件的b的值为:或.
3.解:(1)连接BE,OF,
∵四边形ABCD是矩形,
∴∠A=∠D=90°,AB=CD,
∵∠A=90°,
∴BE是⊙O的直径,
∵点E是AD的中点,
∴EA=ED,
∴△EAB≌△EDC
(SAS),
∴EB=EC,
∴∠EBC=∠ECB,
∵OB=OF,
∴∠EBC=∠OFB,
∴∠ECB=∠OFB,
∴OF∥EC,
∴∠OFH=∠FHC,
∵FH⊥CE,
∴∠FHC=∠OFH=90°,
又∵OF是⊙O的半径,
∴直线FH是⊙O的切线;
(2)EC与⊙O相切,
理由:连接EF,
由(1)得,BE是⊙O的直径,
∴∠EFB=EFC=90°,
∵点H是EC的中点,
∴FH=EH=HC,
∵FH⊥CE,
∴∠FHC=90°,
∴∠ECF=∠HFC=45°,
∵EB=EC,
∴∠EBF=∠ECF=45°,
∴∠BEC=90°,
又∵OE是⊙O的半径,
∴直线EC是⊙O的切线;
由上述可知,四边形ABFE和四边形OFHE都是正方形,
∴AE=AB=AD=×4=2,
∴BE==4,
∴OE=OF=2,
∴S=S正方形OFHE﹣S扇形OEF=22﹣=4﹣π.
4.解:(1)∵BD为∠ABC的角平分线,
∴∠ABD=∠CBD,
∴AD=CD;
(2)连接BO并延长交⊙O于点F,连接CF,则BF为直径,即∠BCF=90°,
又∵BE为⊙O切线,
∴OB⊥BE,即∠OBE=90°=∠BCF,
∴∠EBC+∠FBC=∠FBC+∠F,
∴∠EBC=∠F,
又∵∠F=∠BAC,
∴∠EBC=∠BAC,
又∵CE=CE,
∴△EBC∽△EAB,
∴,
∴BE2=AE?EC=(EC+AC)?EC,
即BE2=10×2,
∴(负值已舍去),
(3)∵x2﹣14x+48=0,(x﹣8)(x﹣6)=0,
∴x1=8,x2=6,
又∵AB>BC,
∴AB=8,BC=6,
又∵∠ABC=180°﹣∠ADC=90°,
∴由勾股定理:,
过A作AH⊥BD交BD于H,
∵∠ADC=90°,AD=DC,
∴,
∴,
又∵∠ABD=∠ACD=45°,
∴,
在Rt△AHD中,
由勾股定理:,
∴.
5.(1)证明:连接OD,如图所示:
∵四边形AOCD为平行四边形,
∴OA=DC,OC=AD,
∵OA=OC=OD,
∴OA=OD=AD,DC=OC=OD,
∴△OAD、△OCD都是等边三角形,
∴∠AOD=∠COD=60°,
∴∠BOC=180°﹣∠AOD﹣∠COD=60°,
在△OBF和△ODF中,
,
∴△OBF≌△ODF(SAS),
∴∠OBF=∠ODF,
∵∠OBF=90°,
∴∠ODF=90°,
∴EF⊥OD
∵点D在⊙O上,
∴EF为⊙O的切线;
(2)解:在Rt△ODE中,∵∠AOD=60°,
∴∠FEB=30°,
∵OD=1,
∴OE=2,DE=OD=,
∴S△EOD=OD×DE=×1×=,S扇形AOD==π,
∴图中阴影部分的面积=S△EOD﹣S扇形AOD=﹣π.
6.解:(1)∵OD⊥AB,
∴=,
∴∠DEB=∠AOD=×50°=25°.
(2)①∵OC=3,OA=5,
∴AC=4,
∵OD⊥AB,
∴==,
∴AC=BC=AB=4,
∴AB=8;
②∵∠AOD=50°,=,
∴∠AOB=100°,
∵OA=5,
∴的长===.
7.(1)证明:∵∠ADC=90°,DE平分∠ADC,
∴∠ADE=45°,
∵∠ABE=∠ADE=45°,
∴△ABC是半直角三角形;
(2)证明:∵OM⊥AB,OA=OB,
∴AD=BD,
∴∠DAB=∠DBA,
∵∠DEB=∠DAB,
∴∠DBA=∠DEB,
∵D、B、A、E四点共圆,
∴∠DBA+∠DEA=180°,
∵∠DEB+∠DEC=180°,
∴∠DEA=∠DEC;
(3)解:如图1,连接AM,ME,设⊙M的半径为r,
∵点D的坐标为(0,8),
∴OM=8﹣r,
由OM2+OA2=MA2得:(8﹣r)2+42=r2,
解得r=5,
∴⊙M
的半径为5,
∵∠ABE=45°,
∴∠EMA=2∠ABE=90°,
∴EA2=MA2+ME2=52+52=50,
∴AE=5.
8.解:(1)∵OD⊥AC,AC=6,
∴AD=3,
∵OD=,
∴OA=4,
∴⊙O的直径=8;
(2)过点E作EF⊥CB,交CB的延长线于点F,
∵AB为直径,
∴∠ACB=∠CDE=∠CFE=90°,
∴四边形CDEF为矩形,
∴EF=CD=AC=3,BC===2,
∴S△BEC=×BC×EF=×3=3.
9.证明:(1)∵CH⊥AB,
∴∠BFH+∠FBH=90°,
∵BE⊥AC,
∴∠A+∠ABE=90°,
∴∠BFH=∠A,
∵∠A=∠D,
∴∠BFH=∠D,
∴BF=BD,
∵BH⊥FD,
∴HD=HF;
(2)连接OD、OB,如图,
∵∠BCD+∠CBH=90°,
∴∠BCH=90°﹣∠CBH=90°﹣60°=30°,
∴∠BOD=2∠BCD=60°,
∵OB=OD,
∴△OBD为等边三角形,
∴BD=OB,
∴BD等于⊙O的半径.
10.解;(1)∵AB是⊙O的直径,
∴∠AEB=90°,
又∵∠BAC=45°,
∴∠ABE=45°.
又∵AB=AC,
∴∠ABC=∠C=67.5°.
∴∠EBC=22.5°;
(2)连接OE,
∵AB是⊙O的直径,
∴∠AEB=90°,
又∵∠BAC=45°,
∴∠ABE=45°.
∴AE=BE,
∵OA=OB,
∴OE⊥AB,
∵OA=OB=OE=2,
∴S阴影=S扇形OBE﹣S△OBE=﹣=﹣=π﹣2.
